Erweitern Sie diese Funktion zu einer Fourier-Reihe. Fourier-Reihe: Geschichte und Einfluss des mathematischen Mechanismus auf die Entwicklung der Wissenschaft

Funktionen, zerlegen sie in Komponenten. Wechselströme und -spannungen, Verschiebungen, Geschwindigkeit und Beschleunigung von Kurbeltrieben sowie akustische Wellen sind typische praktische Beispiele für die Verwendung periodischer Funktionen in technischen Berechnungen.

Die Fourier-Reihenentwicklung basiert auf der Annahme, dass alle Funktionen von praktischer Bedeutung im Intervall -π ≤x≤ π in Form einer konvergenten trigonometrischen Reihe ausgedrückt werden können (eine Reihe gilt als konvergent, wenn die Folge von Teilsummen aus ihren Gliedern besteht konvergiert):

Standard (=gewöhnliche) Notation durch die Summe von Sinx und Cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

wobei a o, a 1,a 2,...,b 1,b 2,.. reelle Konstanten sind, d.h.

Dabei werden für den Bereich von -π bis π die Fourier-Reihenkoeffizienten anhand der Formeln berechnet:

Die Koeffizienten a o , a n und b n werden aufgerufen Fourier-Koeffizienten, und wenn sie gefunden werden können, wird Serie (1) aufgerufen neben Fourier, entsprechend der Funktion f(x). Für die Reihe (1) heißt der Term (a 1 cosx+b 1 sinx) der erste oder Grundharmonische,

Eine andere Möglichkeit, eine Reihe zu schreiben, besteht darin, die Beziehung acosx+bsinx=csin(x+α) zu verwenden.

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

Dabei ist a o eine Konstante, c 1 =(a 1 2 +b 1 2) 1/2, c n =(a n 2 +b n 2) 1/2 sind die Amplituden der verschiedenen Komponenten und ist gleich a n =arctg a n /b n.

Für die Reihe (1) heißt der Term (a 1 cosx+b 1 sinx) oder c 1 sin(x+α 1) der erste oder Grundharmonische,(a 2 cos2x+b 2 sin2x) oder c 2 sin(2x+α 2) heißt zweite Harmonische usw.

Um ein komplexes Signal genau darzustellen, sind typischerweise unendlich viele Terme erforderlich. Bei vielen praktischen Problemen reicht es jedoch aus, nur die ersten paar Begriffe zu berücksichtigen.

Fourierreihe nichtperiodischer Funktionen mit der Periode 2π.

Erweiterung nichtperiodischer Funktionen in Fourier-Reihen.

Wenn die Funktion f(x) nicht periodisch ist, bedeutet dies, dass sie nicht für alle Werte von x zu einer Fourier-Reihe entwickelt werden kann. Es ist jedoch möglich, eine Fourier-Reihe zu definieren, die eine Funktion über einen beliebigen Bereich der Breite 2π darstellt.

Bei einer gegebenen nichtperiodischen Funktion kann eine neue Funktion konstruiert werden, indem Werte von f(x) innerhalb eines bestimmten Bereichs ausgewählt und außerhalb dieses Bereichs in 2π-Intervallen wiederholt werden. Da die neue Funktion periodisch mit der Periode 2π ist, kann sie für alle Werte von x zu einer Fourier-Reihe entwickelt werden. Beispielsweise ist die Funktion f(x)=x nicht periodisch. Wenn es jedoch notwendig ist, es im Intervall von o bis 2π zu einer Fourier-Reihe zu entwickeln, dann wird außerhalb dieses Intervalls eine periodische Funktion mit einer Periode von 2π konstruiert (wie in der Abbildung unten gezeigt).

Für nichtperiodische Funktionen wie f(x)=x ist die Summe der Fourier-Reihe an allen Punkten in einem bestimmten Bereich gleich dem Wert von f(x), für Punkte jedoch nicht gleich f(x). außerhalb des Bereichs. Um die Fourier-Reihe einer nichtperiodischen Funktion im 2π-Bereich zu finden, wird dieselbe Formel für Fourier-Koeffizienten verwendet.

Gerade und ungerade Funktionen.

Sie sagen, die Funktion y=f(x) sogar, wenn f(-x)=f(x) für alle Werte von x. Graphen gerader Funktionen sind immer symmetrisch zur y-Achse (d. h. sie sind Spiegelbilder). Zwei Beispiele für gerade Funktionen: y=x2 und y=cosx.

Sie sagen, dass die Funktion y=f(x) seltsam, wenn f(-x)=-f(x) für alle Werte von x. Graphen ungerader Funktionen sind immer symmetrisch zum Ursprung.

Viele Funktionen sind weder gerade noch ungerade.

Fourier-Reihenentwicklung in Kosinus.

Die Fourier-Reihe einer geraden periodischen Funktion f(x) mit der Periode 2π enthält nur Kosinus-Terme (d. h. keine Sinus-Terme) und kann einen konstanten Term enthalten. Somit,

wo sind die Koeffizienten der Fourier-Reihe,

Die Fourier-Reihe einer ungeraden periodischen Funktion f(x) mit der Periode 2π enthält nur Terme mit Sinuswerten (d. h. sie enthält keine Terme mit Kosinuswerten).

Somit,

wo sind die Koeffizienten der Fourier-Reihe,

Fourier-Reihe im Halbzyklus.

Wenn eine Funktion für einen Bereich definiert ist, beispielsweise von 0 bis π und nicht nur von 0 bis 2π, kann sie in einer Reihe nur in Sinuswerten oder nur in Kosinuswerten entwickelt werden. Die resultierende Fourier-Reihe heißt in der Nähe von Fourier bei halbem Zyklus.

Wenn Sie die Zerlegung erhalten möchten Halbzyklus-Fourier nach Kosinus Funktionen f(x) im Bereich von 0 bis π, dann ist es notwendig, eine gerade periodische Funktion zu konstruieren. In Abb. Unten ist die Funktion f(x)=x, aufgebaut auf dem Intervall von x=0 bis x=π. Da die gerade Funktion symmetrisch zur f(x)-Achse ist, zeichnen wir die Linie AB, wie in Abb. unten. Wenn wir davon ausgehen, dass die resultierende Dreiecksform außerhalb des betrachteten Intervalls periodisch mit einer Periode von 2π ist, dann sieht der endgültige Graph so aus: in Abb. unten. Da wir wie zuvor die Fourier-Entwicklung in Kosinuswerten erhalten müssen, berechnen wir die Fourier-Koeffizienten a o und a n

Wenn Sie Funktionen f(x) im Bereich von 0 bis π erhalten möchten, müssen Sie eine ungerade periodische Funktion konstruieren. In Abb. Unten ist die Funktion f(x)=x, aufgebaut auf dem Intervall von x=0 bis x=π. Da die ungerade Funktion symmetrisch zum Ursprung ist, konstruieren wir die Gerade CD, wie in Abb. Wenn wir davon ausgehen, dass das resultierende Sägezahnsignal außerhalb des betrachteten Intervalls periodisch mit einer Periode von 2π ist, dann hat der endgültige Graph die in Abb. Da wir wie zuvor die Fourier-Entwicklung des Halbzyklus in Form von Sinuswerten erhalten müssen, berechnen wir den Fourier-Koeffizienten. B

Fourier-Reihe für ein beliebiges Intervall.

Erweiterung einer periodischen Funktion mit Periode L.

Die periodische Funktion f(x) wiederholt sich, wenn x um L zunimmt, d. h. f(x+L)=f(x). Der Übergang von den zuvor betrachteten Funktionen mit einer Periode von 2π zu Funktionen mit einer Periode von L ist recht einfach, da er durch einen Variablenwechsel erfolgen kann.

Um die Fourier-Reihe der Funktion f(x) im Bereich -L/2≤x≤L/2 zu finden, führen wir eine neue Variable u ein, sodass die Funktion f(x) eine Periode von 2π relativ zu u hat. Wenn u=2πx/L, dann ist x=-L/2 für u=-π und x=L/2 für u=π. Sei auch f(x)=f(Lu/2π)=F(u). Die Fourier-Reihe F(u) hat die Form

Wo sind die Koeffizienten der Fourier-Reihe,

Allerdings führt die obige Formel häufiger zu einer Abhängigkeit von x. Da u=2πx/L, bedeutet dies du=(2π/L)dx, und die Integrationsgrenzen liegen bei -L/2 bis L/2 statt bei -π bis π. Folglich hat die Fourier-Reihe für die Abhängigkeit von x die Form

wobei im Bereich von -L/2 bis L/2 die Koeffizienten der Fourier-Reihe liegen,

(Die Integrationsgrenzen können durch ein beliebiges Intervall der Länge L ersetzt werden, zum Beispiel von 0 bis L)

Fourier-Reihe auf einer Halbwelle für Funktionen, die im Intervall L≠2π angegeben sind.

Für die Substitution u=πх/L entspricht das Intervall von x=0 bis x=L dem Intervall von u=0 bis u=π. Folglich kann die Funktion nur in Kosinus- oder nur in Sinusreihen zu einer Reihe entwickelt werden, d. h. V Fourier-Reihe im Halbzyklus.

Die Kosinusentwicklung im Bereich von 0 bis L hat die Form

Fourierreihe periodischer Funktionen mit der Periode 2π.

Die Fourier-Reihe ermöglicht es uns, periodische Funktionen zu untersuchen, indem wir sie in Komponenten zerlegen. Wechselströme und -spannungen, Verschiebungen, Geschwindigkeit und Beschleunigung von Kurbeltrieben sowie akustische Wellen sind typische praktische Beispiele für die Verwendung periodischer Funktionen in technischen Berechnungen.

Die Fourier-Reihenentwicklung basiert auf der Annahme, dass alle Funktionen von praktischer Bedeutung im Intervall -π ≤x≤ π in Form einer konvergenten trigonometrischen Reihe ausgedrückt werden können (eine Reihe gilt als konvergent, wenn die Folge von Teilsummen aus ihren Gliedern besteht konvergiert):

Standard (=gewöhnliche) Notation durch die Summe von Sinx und Cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

wobei a o, a 1,a 2,...,b 1,b 2,.. reelle Konstanten sind, d.h.

Dabei werden für den Bereich von -π bis π die Fourier-Reihenkoeffizienten anhand der Formeln berechnet:

Die Koeffizienten a o , a n und b n werden aufgerufen Fourier-Koeffizienten, und wenn sie gefunden werden können, wird Serie (1) aufgerufen neben Fourier, entsprechend der Funktion f(x). Für die Reihe (1) heißt der Term (a 1 cosx+b 1 sinx) der erste oder Grundharmonische,

Eine andere Möglichkeit, eine Reihe zu schreiben, besteht darin, die Beziehung acosx+bsinx=csin(x+α) zu verwenden.

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

Dabei ist a o eine Konstante, c 1 =(a 1 2 +b 1 2) 1/2, c n =(a n 2 +b n 2) 1/2 sind die Amplituden der verschiedenen Komponenten und ist gleich a n =arctg a n /b n.

Für die Reihe (1) heißt der Term (a 1 cosx+b 1 sinx) oder c 1 sin(x+α 1) der erste oder Grundharmonische,(a 2 cos2x+b 2 sin2x) oder c 2 sin(2x+α 2) heißt zweite Harmonische usw.

Um ein komplexes Signal genau darzustellen, sind typischerweise unendlich viele Terme erforderlich. Bei vielen praktischen Problemen reicht es jedoch aus, nur die ersten paar Begriffe zu berücksichtigen.

Fourierreihe nichtperiodischer Funktionen mit der Periode 2π.

Erweiterung nichtperiodischer Funktionen.

Wenn die Funktion f(x) nicht periodisch ist, bedeutet dies, dass sie nicht für alle Werte von x zu einer Fourier-Reihe entwickelt werden kann. Es ist jedoch möglich, eine Fourier-Reihe zu definieren, die eine Funktion über einen beliebigen Bereich der Breite 2π darstellt.

Bei einer gegebenen nichtperiodischen Funktion kann eine neue Funktion konstruiert werden, indem Werte von f(x) innerhalb eines bestimmten Bereichs ausgewählt und außerhalb dieses Bereichs in 2π-Intervallen wiederholt werden. Da die neue Funktion periodisch mit der Periode 2π ist, kann sie für alle Werte von x zu einer Fourier-Reihe entwickelt werden. Beispielsweise ist die Funktion f(x)=x nicht periodisch. Wenn es jedoch notwendig ist, es im Intervall von o bis 2π zu einer Fourier-Reihe zu entwickeln, dann wird außerhalb dieses Intervalls eine periodische Funktion mit einer Periode von 2π konstruiert (wie in der Abbildung unten gezeigt).

Für nichtperiodische Funktionen wie f(x)=x ist die Summe der Fourier-Reihe an allen Punkten in einem bestimmten Bereich gleich dem Wert von f(x), für Punkte jedoch nicht gleich f(x). außerhalb des Bereichs. Um die Fourier-Reihe einer nichtperiodischen Funktion im 2π-Bereich zu finden, wird dieselbe Formel für Fourier-Koeffizienten verwendet.

Gerade und ungerade Funktionen.

Sie sagen, die Funktion y=f(x) sogar, wenn f(-x)=f(x) für alle Werte von x. Graphen gerader Funktionen sind immer symmetrisch zur y-Achse (d. h. sie sind Spiegelbilder). Zwei Beispiele für gerade Funktionen: y=x2 und y=cosx.

Sie sagen, dass die Funktion y=f(x) seltsam, wenn f(-x)=-f(x) für alle Werte von x. Graphen ungerader Funktionen sind immer symmetrisch zum Ursprung.

Viele Funktionen sind weder gerade noch ungerade.

Fourier-Reihenentwicklung in Kosinus.

Die Fourier-Reihe einer geraden periodischen Funktion f(x) mit der Periode 2π enthält nur Kosinus-Terme (d. h. keine Sinus-Terme) und kann einen konstanten Term enthalten. Somit,

wo sind die Koeffizienten der Fourier-Reihe,

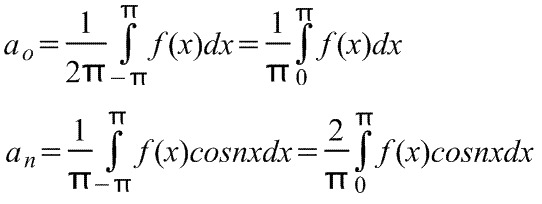
Die Fourier-Reihe einer ungeraden periodischen Funktion f(x) mit der Periode 2π enthält nur Terme mit Sinuswerten (d. h. sie enthält keine Terme mit Kosinuswerten).

Somit,

wo sind die Koeffizienten der Fourier-Reihe,

Fourier-Reihe im Halbzyklus.

Wenn eine Funktion für einen Bereich definiert ist, beispielsweise von 0 bis π und nicht nur von 0 bis 2π, kann sie in einer Reihe nur in Sinuswerten oder nur in Kosinuswerten entwickelt werden. Die resultierende Fourier-Reihe heißt in der Nähe von Fourier bei halbem Zyklus.

Wenn Sie die Zerlegung erhalten möchten Halbzyklus-Fourier nach Kosinus Funktionen f(x) im Bereich von 0 bis π, dann ist es notwendig, eine gerade periodische Funktion zu konstruieren. In Abb. Unten ist die Funktion f(x)=x, aufgebaut auf dem Intervall von x=0 bis x=π. Da die gerade Funktion symmetrisch zur f(x)-Achse ist, zeichnen wir die Linie AB, wie in Abb. unten. Wenn wir davon ausgehen, dass die resultierende Dreiecksform außerhalb des betrachteten Intervalls periodisch mit einer Periode von 2π ist, dann sieht der endgültige Graph so aus: in Abb. unten. Da wir wie zuvor die Fourier-Entwicklung in Kosinuswerten erhalten müssen, berechnen wir die Fourier-Koeffizienten a o und a n

Wenn Sie es brauchen Fourier-Halbzyklus-Sinusentwicklung Funktionen f(x) im Bereich von 0 bis π, dann ist es notwendig, eine ungerade periodische Funktion zu konstruieren. In Abb. Unten ist die Funktion f(x)=x, aufgebaut auf dem Intervall von x=0 bis x=π. Da die ungerade Funktion symmetrisch zum Ursprung ist, konstruieren wir die Gerade CD, wie in Abb. Wenn wir davon ausgehen, dass das resultierende Sägezahnsignal außerhalb des betrachteten Intervalls periodisch mit einer Periode von 2π ist, dann hat der endgültige Graph die in Abb. Da wir wie zuvor die Fourier-Entwicklung des Halbzyklus in Form von Sinuswerten erhalten müssen, berechnen wir den Fourier-Koeffizienten. B

Fourier-Reihe für ein beliebiges Intervall.

Erweiterung einer periodischen Funktion mit Periode L.

Die periodische Funktion f(x) wiederholt sich, wenn x um L zunimmt, d. h. f(x+L)=f(x). Der Übergang von den zuvor betrachteten Funktionen mit einer Periode von 2π zu Funktionen mit einer Periode von L ist recht einfach, da er durch einen Variablenwechsel erfolgen kann.

Um die Fourier-Reihe der Funktion f(x) im Bereich -L/2≤x≤L/2 zu finden, führen wir eine neue Variable u ein, sodass die Funktion f(x) eine Periode von 2π relativ zu u hat. Wenn u=2πx/L, dann ist x=-L/2 für u=-π und x=L/2 für u=π. Sei auch f(x)=f(Lu/2π)=F(u). Die Fourier-Reihe F(u) hat die Form

(Die Integrationsgrenzen können durch ein beliebiges Intervall der Länge L ersetzt werden, zum Beispiel von 0 bis L)

Fourier-Reihe auf einer Halbwelle für Funktionen, die im Intervall L≠2π angegeben sind.

Für die Substitution u=πх/L entspricht das Intervall von x=0 bis x=L dem Intervall von u=0 bis u=π. Folglich kann die Funktion nur in Kosinus- oder nur in Sinusreihen zu einer Reihe entwickelt werden, d. h. V Fourier-Reihe im Halbzyklus.

Die Kosinusentwicklung im Bereich von 0 bis L hat die Form

Fourierreihen sind die Darstellung einer beliebigen Funktion mit einer bestimmten Periode in Form einer Reihe. Im Allgemeinen wird diese Lösung als Zerlegung eines Elements entlang einer orthogonalen Basis bezeichnet. Die Erweiterung von Funktionen in Fourier-Reihen ist aufgrund der Eigenschaften dieser Transformation während der Integration, Differentiation sowie der Verschiebung von Ausdrücken durch Argument und Faltung ein ziemlich leistungsfähiges Werkzeug zur Lösung verschiedener Probleme.

Wer sich mit höherer Mathematik und den Werken des französischen Wissenschaftlers Fourier nicht auskennt, wird höchstwahrscheinlich nicht verstehen, was diese „Reihen“ sind und wofür sie benötigt werden. Mittlerweile ist dieser Wandel in unser Leben integriert. Es wird nicht nur von Mathematikern, sondern auch von Physikern, Chemikern, Ärzten, Astronomen, Seismologen, Ozeanographen und vielen anderen verwendet. Werfen wir auch einen genaueren Blick auf die Werke des großen französischen Wissenschaftlers, der eine Entdeckung machte, die seiner Zeit voraus war.

Der Mensch und die Fourier-Transformation

Fourier-Reihen sind eine der Methoden (neben der Analyse und anderen). Dieser Prozess findet jedes Mal statt, wenn eine Person einen Ton hört. Unser Ohr wandelt Elementarteilchen in einem elastischen Medium automatisch in Reihen (entlang des Spektrums) aufeinanderfolgender Lautstärkepegel für Töne unterschiedlicher Höhe um. Anschließend wandelt das Gehirn diese Daten in Geräusche um, die uns vertraut sind. All dies geschieht ohne unseren Wunsch oder unser Bewusstsein, von selbst, aber um diese Prozesse zu verstehen, wird es mehrere Jahre dauern, höhere Mathematik zu studieren.

Mehr zur Fourier-Transformation

Die Fourier-Transformation kann mit analytischen, numerischen und anderen Methoden durchgeführt werden. Fourier-Reihen beziehen sich auf die numerische Methode zur Zerlegung jeglicher Oszillationsprozesse – von Meeresgezeiten und Lichtwellen bis hin zu Zyklen der Sonnenaktivität (und anderer astronomischer Objekte). Mit diesen mathematischen Techniken können Sie Funktionen analysieren und beliebige Schwingungsprozesse als eine Reihe sinusförmiger Komponenten darstellen, die sich vom Minimum zum Maximum und zurück bewegen. Die Fourier-Transformation ist eine Funktion, die die Phase und Amplitude von Sinuskurven beschreibt, die einer bestimmten Frequenz entsprechen. Mit diesem Verfahren lassen sich sehr komplexe Gleichungen lösen, die dynamische Prozesse beschreiben, die unter dem Einfluss von thermischer, Licht- oder elektrischer Energie entstehen. Darüber hinaus ermöglichen Fourier-Reihen die Isolierung konstanter Komponenten in komplexen Schwingungssignalen und ermöglichen so die korrekte Interpretation experimenteller Beobachtungen in Medizin, Chemie und Astronomie.

Historische Referenz

Der Begründer dieser Theorie ist der französische Mathematiker Jean Baptiste Joseph Fourier. Diese Transformation wurde später nach ihm benannt. Zunächst untersuchte und erklärte der Wissenschaftler mit seiner Methode die Mechanismen der Wärmeleitfähigkeit – der Ausbreitung von Wärme in Festkörpern. Fourier schlug vor, dass die anfängliche unregelmäßige Verteilung in einfache Sinuskurven zerlegt werden kann, von denen jede ihr eigenes Temperaturminimum und -maximum sowie ihre eigene Phase aufweist. In diesem Fall wird jede dieser Komponenten vom Minimum zum Maximum und zurück gemessen. Die mathematische Funktion, die die oberen und unteren Spitzen der Kurve sowie die Phase jeder der Harmonischen beschreibt, wird Fourier-Transformation des Temperaturverteilungsausdrucks genannt. Der Autor der Theorie reduzierte die mathematisch schwer zu beschreibende allgemeine Verteilungsfunktion auf eine sehr praktische Reihe von Kosinus und Sinus, die zusammen die ursprüngliche Verteilung ergeben.

Das Prinzip der Transformation und die Ansichten der Zeitgenossen

Die Zeitgenossen des Wissenschaftlers – führende Mathematiker des frühen 19. Jahrhunderts – akzeptierten diese Theorie nicht. Der Haupteinwand war Fouriers Behauptung, dass eine unstetige Funktion, die eine gerade Linie oder eine unstetige Kurve beschreibt, als Summe stetiger Sinusausdrücke dargestellt werden kann. Betrachten Sie als Beispiel den Heaviside-Schritt: Sein Wert ist links von der Diskontinuität Null und rechts von eins. Diese Funktion beschreibt die Abhängigkeit des elektrischen Stroms von einer temporären Größe bei geschlossenem Stromkreis. Zeitgenossen der Theorie hatten zu dieser Zeit noch nie eine ähnliche Situation erlebt, in der ein diskontinuierlicher Ausdruck durch eine Kombination kontinuierlicher, gewöhnlicher Funktionen wie Exponential-, Sinus-, Linear- oder Quadratfunktionen beschrieben würde.

Was verwirrte französische Mathematiker an Fouriers Theorie?

Denn wenn der Mathematiker mit seinen Aussagen Recht hatte, dann kann man durch Summieren der unendlichen trigonometrischen Fourier-Reihe eine genaue Darstellung des Stufenausdrucks erhalten, auch wenn dieser viele ähnliche Schritte hat. Zu Beginn des 19. Jahrhunderts erschien eine solche Aussage absurd. Trotz aller Zweifel erweiterten viele Mathematiker den Umfang der Untersuchung dieses Phänomens und gingen über die Untersuchung der Wärmeleitfähigkeit hinaus. Die meisten Wissenschaftler quälten sich jedoch weiterhin mit der Frage: „Kann die Summe einer Sinusreihe zum exakten Wert der unstetigen Funktion konvergieren?“

Konvergenz von Fourier-Reihen: ein Beispiel

Die Frage der Konvergenz stellt sich immer dann, wenn es darum geht, unendliche Zahlenreihen zu summieren. Um dieses Phänomen zu verstehen, betrachten Sie ein klassisches Beispiel. Werden Sie jemals die Wand erreichen können, wenn jede weitere Stufe halb so groß ist wie die vorherige? Nehmen wir an, Sie sind zwei Meter von Ihrem Ziel entfernt, der erste Schritt führt Sie zur Halbzeitmarke, der nächste zur Dreiviertelmarke und nach dem fünften Schritt haben Sie fast 97 Prozent des Weges zurückgelegt. Doch egal wie viele Schritte Sie unternehmen, Sie werden Ihr angestrebtes Ziel im strengen mathematischen Sinne nicht erreichen. Mithilfe numerischer Berechnungen kann nachgewiesen werden, dass es letztendlich möglich ist, bis zu einer bestimmten Entfernung heranzukommen. Dieser Beweis ist gleichbedeutend mit dem Nachweis, dass die Summe von einer Hälfte, einem Viertel usw. gegen Eins tendiert.

Die Frage der Konvergenz: Das Zweite Kommen oder Lord Kelvins Instrument

Diese Frage wurde Ende des 19. Jahrhunderts erneut aufgeworfen, als man versuchte, Fourier-Reihen zur Vorhersage der Intensität von Gezeiten zu verwenden. Zu dieser Zeit erfand Lord Kelvin ein Instrument, ein analoges Computergerät, das es Militär- und Handelsschiffen ermöglichte, dieses Naturphänomen zu überwachen. Dieser Mechanismus bestimmte Phasen- und Amplitudensätze aus einer Tabelle mit Gezeitenhöhen und entsprechenden Zeitpunkten, die das ganze Jahr über in einem bestimmten Hafen sorgfältig gemessen wurden. Jeder Parameter war eine sinusförmige Komponente des Gezeitenhöhenausdrucks und eine der regulären Komponenten. Die Messungen wurden in Lord Kelvins Recheninstrument eingespeist, das eine Kurve synthetisierte, die den Wasserstand als Funktion der Zeit für das folgende Jahr vorhersagte. Schon bald wurden ähnliche Kurven für alle Häfen der Welt erstellt.

Was passiert, wenn der Prozess durch eine diskontinuierliche Funktion gestört wird?

Zu diesem Zeitpunkt schien es offensichtlich, dass ein Flutwellen-Prädiktor mit einer großen Anzahl von Zählelementen eine große Anzahl von Phasen und Amplituden berechnen und so genauere Vorhersagen liefern konnte. Es stellte sich jedoch heraus, dass dieses Muster nicht in Fällen beobachtet wird, in denen der zu synthetisierende Gezeitenausdruck einen scharfen Sprung enthielt, also diskontinuierlich war. Werden Daten aus einer Tabelle mit Zeitmomenten in das Gerät eingegeben, berechnet es mehrere Fourier-Koeffizienten. Dank der Sinuskomponenten (entsprechend den gefundenen Koeffizienten) wird die ursprüngliche Funktion wiederhergestellt. Die Diskrepanz zwischen dem ursprünglichen und dem rekonstruierten Ausdruck kann an jedem Punkt gemessen werden. Bei wiederholten Berechnungen und Vergleichen wird deutlich, dass der Wert des größten Fehlers nicht abnimmt. Sie sind jedoch in dem Bereich lokalisiert, der dem Diskontinuitätspunkt entspricht, und an jedem anderen Punkt tendieren sie gegen Null. Im Jahr 1899 wurde dieses Ergebnis von Joshua Willard Gibbs von der Yale University theoretisch bestätigt.

Konvergenz von Fourierreihen und die Entwicklung der Mathematik im Allgemeinen

Die Fourier-Analyse ist nicht auf Ausdrücke anwendbar, die eine unendliche Anzahl von Spitzen über ein bestimmtes Intervall enthalten. Im Allgemeinen konvergieren Fourier-Reihen immer, wenn die ursprüngliche Funktion durch das Ergebnis einer realen physikalischen Messung dargestellt wird. Fragen zur Konvergenz dieses Prozesses für bestimmte Funktionsklassen führten zur Entstehung neuer Zweige der Mathematik, beispielsweise der Theorie verallgemeinerter Funktionen. Sie wird mit Namen wie L. Schwartz, J. Mikusinski und J. Temple in Verbindung gebracht. Im Rahmen dieser Theorie wurde eine klare und präzise theoretische Grundlage für Ausdrücke wie die Dirac-Delta-Funktion (sie beschreibt einen Bereich einer einzelnen Fläche, die in einer infinitesimalen Umgebung eines Punktes konzentriert ist) und den Heaviside-„Schritt“ geschaffen. Dank dieser Arbeit wurden Fourier-Reihen zur Lösung von Gleichungen und Problemen mit intuitiven Konzepten anwendbar: Punktladung, Punktmasse, magnetische Dipole und konzentrierte Last auf einen Balken.

Fourier-Methode

Fourier-Reihen beginnen gemäß den Interferenzprinzipien mit der Zerlegung komplexer Formen in einfachere. Beispielsweise wird eine Änderung des Wärmeflusses durch seinen Durchgang durch verschiedene Hindernisse aus wärmeisolierendem Material unregelmäßiger Form oder durch eine Änderung der Erdoberfläche – ein Erdbeben, eine Änderung der Umlaufbahn eines Himmelskörpers – durch den Einfluss erklärt von Planeten. In der Regel lassen sich solche Gleichungen, die einfache klassische Systeme beschreiben, für jede einzelne Welle leicht lösen. Fourier zeigte, dass einfache Lösungen auch summiert werden können, um Lösungen für komplexere Probleme zu erhalten. In mathematischer Hinsicht sind Fourier-Reihen eine Technik zur Darstellung eines Ausdrucks als Summe von Harmonischen – Kosinus und Sinus. Daher wird diese Analyse auch als „harmonische Analyse“ bezeichnet.

Fourier-Reihe – eine ideale Technik vor dem „Computerzeitalter“

Vor der Entwicklung der Computertechnologie war die Fourier-Technik die beste Waffe im Arsenal der Wissenschaftler, wenn es um die Wellennatur unserer Welt ging. Die Fourier-Reihe in komplexer Form ermöglicht es, nicht nur einfache Probleme zu lösen, die der direkten Anwendung der Newtonschen Gesetze der Mechanik zugänglich sind, sondern auch grundlegende Gleichungen. Die meisten Entdeckungen der Newtonschen Wissenschaft im 19. Jahrhundert wurden nur durch Fouriers Technik ermöglicht.

Fourier-Reihe heute

Mit der Entwicklung von Computern haben Fourier-Transformationen ein qualitativ neues Niveau erreicht. Diese Technik ist in fast allen Bereichen der Wissenschaft und Technik fest etabliert. Ein Beispiel ist digitales Audio und Video. Ihre Umsetzung wurde erst dank einer Theorie möglich, die ein französischer Mathematiker zu Beginn des 19. Jahrhunderts entwickelte. Somit ermöglichte die Fourier-Reihe in komplexer Form einen Durchbruch in der Erforschung des Weltraums. Darüber hinaus beeinflusste es das Studium der Physik von Halbleitermaterialien und Plasma, der Mikrowellenakustik, der Ozeanographie, des Radars und der Seismologie.

Trigonometrische Fourier-Reihe

In der Mathematik ist eine Fourier-Reihe eine Möglichkeit, beliebige komplexe Funktionen als Summe einfacherer Funktionen darzustellen. Im Allgemeinen kann die Anzahl solcher Ausdrücke unendlich sein. Darüber hinaus ist das Endergebnis umso genauer, je stärker ihre Anzahl bei der Berechnung berücksichtigt wird. Am häufigsten werden trigonometrische Funktionen des Kosinus oder Sinus als einfachste verwendet. In diesem Fall werden Fourier-Reihen als trigonometrisch bezeichnet, und die Lösung solcher Ausdrücke wird als harmonische Entwicklung bezeichnet. Diese Methode spielt in der Mathematik eine wichtige Rolle. Erstens bietet die trigonometrische Reihe ein Mittel zur Darstellung und auch zum Studium von Funktionen; sie ist der Hauptapparat der Theorie. Darüber hinaus können Sie damit eine Reihe von Problemen der mathematischen Physik lösen. Schließlich trug diese Theorie zur Entwicklung einer Reihe sehr wichtiger Zweige der mathematischen Wissenschaft bei (der Integraltheorie, der Theorie der periodischen Funktionen). Darüber hinaus diente es als Ausgangspunkt für die Entwicklung der folgenden Funktionen einer reellen Variablen und legte den Grundstein für die harmonische Analyse.

Fourier-Reihenentwicklung gerader und ungerader Funktionen Entwicklung einer auf einem Intervall gegebenen Funktion in eine Reihe in Sinus oder Cosinus Fourier-Reihe für eine Funktion mit beliebiger Periode Komplexe Darstellung der Fourier-Reihe Fourier-Reihe in allgemeinen orthogonalen Funktionssystemen Fourier-Reihe in einer Orthogonales System Minimale Eigenschaft von Fourier-Koeffizienten Besselsche Ungleichung Gleichheit Parseval Geschlossene Systeme Vollständigkeit und Geschlossenheit von Systemen

Fourier-Reihenentwicklung gerader und ungerader Funktionen Eine Funktion f(x), definiert auf dem Intervall \-1, wobei I > 0, heißt gerade, wenn der Graph der geraden Funktion symmetrisch zur Ordinatenachse ist. Eine auf der Strecke J definierte Funktion f(x) mit I > 0 heißt ungerade, wenn der Graph der ungeraden Funktion symmetrisch zum Ursprung ist. Beispiel. a) Die Funktion ist gerade im Intervall |-jt, jt), da für alle x e b) Die Funktion ungerade ist, da die Fourier-Reihenentwicklung gerader und ungerader Funktionen die Entwicklung einer auf einem Intervall gegebenen Funktion in eine Reihe in Sinus- oder Sinusreihen ist Kosinus Fourier-Reihe für eine Funktion mit beliebiger Periode Komplexe Darstellung der Fourier-Reihe Fourier-Reihe für allgemeine orthogonale Funktionssysteme Fourier-Reihe für ein orthogonales System Minimale Eigenschaft von Fourier-Koeffizienten Besselsche Ungleichung Parsevalsche Gleichheit Geschlossene Systeme Vollständigkeit und Geschlossenheit von Systemen c) Funktion f (x)=x2-x, wobei weder zu geraden noch zu ungeraden Funktionen gehört, da die Funktion f(x), die die Bedingungen von Satz 1 erfüllt, im Intervall x| gerade sei. Dann für alle, d.h. /(x) cos nx ist eine gerade Funktion und f(x) sinnx ist eine ungerade Funktion. Daher sind die Fourier-Koeffizienten einer geraden Funktion f(x) gleich. Daher hat die Fourier-Reihe einer geraden Funktion die Form f(x) sin х – eine gerade Funktion. Daher erhalten wir: Somit hat die Fourier-Reihe einer ungeraden Funktion die Form Beispiel 1. Erweitern Sie die Funktion 4 zu einer Fourier-Reihe im Intervall -x ^ x ^ n. Da diese Funktion gerade ist und die Bedingungen von Satz 1 erfüllt, dann hat seine Fourier-Reihe die Form Finden Sie die Fourier-Koeffizienten. Wenn wir die partielle Integration zweimal anwenden, erhalten wir Folgendes: Die Fourier-Reihe dieser Funktion sieht also wie folgt aus: oder, in erweiterter Form, Diese Gleichheit gilt für jedes x €, da an den Punkten x = ±ir die Summe der Reihe fällt mit den Werten der Funktion f(x ) = x2 zusammen, da die Graphen der Funktion f(x) = x und die Summe der resultierenden Reihe in Abb. angegeben sind. Kommentar. Mit dieser Fourier-Reihe können wir die Summe einer der konvergenten Zahlenreihen ermitteln, nämlich für x = 0 erhalten wir das Beispiel 2. Erweitern Sie die Funktion /(x) = x zu einer Fourier-Reihe auf dem Intervall. Die Funktion /(x) erfüllt die Bedingungen von Satz 1, daher kann sie zu einer Fourier-Reihe entwickelt werden, die aufgrund der Seltsamkeit dieser Funktion die Form hat. Durch partielle Integration finden wir die Fourier-Koeffizienten Die Fourier-Reihe dieser Funktion hat die Form Diese Gleichheit gilt für alle x B an den Punkten x - ±t. Die Summe der Fourier-Reihe stimmt nicht mit den Werten der Funktion /(x) = x überein, da sie gleich ist . Außerhalb des Intervalls [-*, i-] ist die Summe der Reihe eine periodische Fortsetzung der Funktion /(x) = x; sein Diagramm ist in Abb. dargestellt. 6. § 6. Entwicklung einer auf einem Intervall gegebenen Funktion in eine Reihe in Sinus oder Cosinus Es sei eine beschränkte stückweise monotone Funktion / auf dem Intervall gegeben. Die Werte dieser Funktion im Intervall 0| kann auf verschiedene Weise weiter definiert werden. Sie können beispielsweise eine Funktion / für das Segment tc] definieren, sodass /. In diesem Fall sagen sie: „auf gleichmäßige Weise bis zum Segment 0 ausgedehnt“; seine Fourier-Reihe enthält nur Kosinuswerte. Wenn die Funktion /(x) auf dem Intervall [-l-, mc] definiert ist, so dass /(, dann ist das Ergebnis eine ungerade Funktion, und dann sagt man, dass / „auf das Intervall [-*, 0] erweitert wird“ In diesem Fall enthält die Fourier-Reihe nur Sinuswerte. Somit kann jede auf dem Intervall definierte begrenzte stückweise monotone Funktion in eine Fourier-Reihe in Beispiel 1 entwickelt werden . Die Funktion kann zu einer Fourier-Reihe entwickelt werden: a) durch Kosinuswerte; b) durch Sinus. M Diese Funktion mit ihren geraden und ungeraden Fortsetzungen in das Segment |-x,0) wird beschränkt und stückweise monoton sein. a) Erweitern wir /(z) in das Segment 0) a) Erweitern wir j\x) in gerader Weise in das Segment (-тр,0| (Abb. 7), dann hat seine Fourier-Reihe i die Form П= 1, wobei die Fourier-Koeffizienten jeweils gleich sind. Daher b) Erweitern wir /(z) auf ungerade Weise in das Segment [-x,0] (Abb. 8). Dann ist seine Fourier-Reihe §7. Fourier-Reihe für eine Funktion mit einer beliebigen Periode Die Funktion fix) sei periodisch mit einer Periode von 21,1 ^ 0. Um sie in eine Fourier-Reihe auf dem Intervall zu erweitern, in dem I > 0 ist, ändern wir die Variable, indem wir x = jt setzen . Dann ist die Funktion F(t) = / ^tj eine periodische Funktion des Arguments t mit Periode und kann auf dem Segment in eine Fourier-Reihe erweitert werden. Zurück zur Variablen x, d. h. zur Einstellung, erhalten wir alle gültigen Sätze für Fourier-Reihen periodischer Funktionen mit Periode 2π, bleiben für periodische Funktionen mit beliebiger Periode gültig 21. Insbesondere bleibt auch ein hinreichendes Kriterium für die Zerlegbarkeit einer Funktion in eine Fourier-Reihe gültig. Beispiel 1. Erweitern Sie eine periodische Funktion mit einer Periode von 21, die im Intervall [-/,/] durch die Formel gegeben ist, in eine Fourier-Reihe (Abb. 9). Da diese Funktion gerade ist, hat ihre Fourier-Reihe die Form. Durch Einsetzen der gefundenen Werte der Fourier-Koeffizienten in die Fourier-Reihe erhalten wir eine wichtige Eigenschaft periodischer Funktionen. Satz 5. Wenn eine Funktion die Periode T hat und integrierbar ist, dann gilt für jede Zahl a die Gleichheit m. das heißt, das Integral über ein Segment, dessen Länge gleich der Periode T ist, hat unabhängig von der Position dieses Segments auf der Zahlenachse den gleichen Wert. Tatsächlich nehmen wir eine Änderung der Variablen im zweiten Integral vor, vorausgesetzt. Dies ergibt und daher bedeutet diese Eigenschaft geometrisch, dass im Fall der in Abb. schattierten Fläche 10 Bereiche sind einander gleich. Insbesondere für eine Funktion f(x) mit einer Periode erhalten wir bei der Erweiterung in eine Fourier-Reihe gerader und ungerader Funktionen die Entwicklung einer auf einem Intervall gegebenen Funktion in eine Reihe in Sinus- oder Cosinus-Fourier-Reihen für eine Funktion mit einer beliebigen Periode Komplexe Notation der Fourier-Reihe Fourier-Reihe in allgemeinen orthogonalen Systemen Funktionen Fourier-Reihe in einem orthogonalen System Minimale Eigenschaft von Fourier-Koeffizienten Besselsche Ungleichung Parsevalsche Gleichheit Geschlossene Systeme Vollständigkeit und Geschlossenheit von Systemen Beispiel 2. Die Funktion x ist periodisch mit einer Periode Aufgrund der Ungeradheit dieser Funktion, ohne Integrale zu berechnen, können wir das für jede feststellen. Die nachgewiesene Eigenschaft zeigt insbesondere, dass die Fourier-Koeffizienten einer periodischen Funktion f(x) mit einer Periode von 21 mithilfe der Formeln berechnet werden können, wobei a ein ist beliebige reelle Zahl (beachten Sie, dass die Funktionen cos - und sin eine Periode von 2/ haben). Beispiel 3. Erweitern Sie eine Funktion, die auf einem Intervall mit einer Periode von 2x gegeben ist, in eine Fourier-Reihe (Abb. 11). 4 Finden wir die Fourier-Koeffizienten dieser Funktion. Wenn wir die Formeln einsetzen, finden wir, dass die Fourier-Reihe daher wie folgt aussehen wird: Am Punkt x = jt (Diskontinuitätspunkt erster Art) haben wir §8. Komplexe Aufzeichnung der Fourier-Reihe In diesem Abschnitt werden einige Elemente der komplexen Analyse verwendet (siehe Kapitel XXX, wo alle hier durchgeführten Aktionen mit komplexen Ausdrücken streng begründet sind). Die Funktion f(x) soll ausreichende Bedingungen für die Entwicklung in einer Fourier-Reihe erfüllen. Dann kann es auf dem Segment x] durch eine Reihe der Form dargestellt werden. Unter Verwendung der Euler-Formeln. Wenn wir diese Ausdrücke in Reihe (1) anstelle von cos px und sin px einsetzen, erhalten wir die folgende Notation. Dann nimmt Reihe (2) an Form Somit wird die Fourier-Reihe (1) in komplexer Form (3) dargestellt. Finden wir Ausdrücke für die Koeffizienten durch Integrale. Wir haben In ähnlicher Weise finden wir, dass die endgültigen Formeln für с„, с_п und с wie folgt geschrieben werden können: . . Die Koeffizienten c werden als komplexe Fourier-Koeffizienten der Funktion bezeichnet. Für eine periodische Funktion mit einer Periode nimmt die komplexe Form der Fourier-Reihe die Form an, bei der die Koeffizienten Cn mithilfe der Formeln berechnet werden ) und (4) werden wie folgt verstanden: Die Reihen (3) und (4) heißen für gegebene Werte konvergent, wenn es Grenzwerte gibt Beispiel. Erweitern Sie die Periodenfunktion zu einer komplexen Fourier-Reihe. Diese Funktion erfüllt ausreichende Bedingungen für die Entwicklung zu einer Fourier-Reihe. Finden wir die komplexen Fourier-Koeffizienten dieser Funktion. Wir haben für ungerades für gerades n, oder kurz gesagt. Durch Einsetzen der Werte erhalten wir schließlich: Beachten Sie, dass diese Reihe auch wie folgt geschrieben werden kann: Fourier-Reihe für allgemeine orthogonale Funktionensysteme 9.1. Orthogonale Funktionensysteme Bezeichnen wir mit der Menge aller (reellen) Funktionen, die auf dem Intervall [a, 6] mit einem Quadrat definiert und integrierbar sind, also derjenigen, für die ein Integral existiert. Insbesondere sind alle Funktionen f(x) stetig auf dem Intervall [a , 6], gehören zu 6], und die Werte ihrer Lebesgue-Integrale stimmen mit den Werten der Riemann-Integrale überein. Definition. Ein System von Funktionen, wo, heißt orthogonal auf dem Intervall [a, b\, wenn Bedingung (1) insbesondere annimmt, dass keine der Funktionen identisch Null ist. Das Integral wird im Sinne von Lebesgue verstanden. und wir nennen die Größe die Norm der Funktion. Wenn wir in einem orthogonalen System für jedes n haben, dann heißt das Funktionensystem orthonormal. Wenn das System (y>„(x)) orthogonal ist, dann ist das System Beispiel 1. Das trigonometrische System ist orthogonal auf einer Strecke. Das Funktionensystem ist ein orthonormales Funktionensystem, Beispiel 2. Das Kosinussystem und das Sinussystem sind orthonormal. Führen wir die Notation ein, dass sie orthogonal auf dem Intervall (0, f|, aber nicht orthonormal (für I Ф- 2) sind. Da ihre Normen COS-Beispiel 3 sind. Durch Gleichheit definierte Polynome werden Legendre-Polynome (Polynome) genannt. Für n = 0 Wir können beweisen, dass die Funktionen ein orthonormales System von Funktionen auf dem Intervall bilden. Lassen Sie uns zum Beispiel die Orthogonalität der Legendre-Polynome zeigen, indem wir n-mal nach Teilen integrieren , finden wir, dass für die Funktion t/m = (z2 - I)m alle Ableitungen bis einschließlich der Ordnung m - I an den Enden des Segments [-1,1) verschwinden. Definition. Ein Funktionensystem (pn(x)) heißt orthogonal auf dem Intervall (a, b) durch einen Überhang p(x), wenn: 1) es für alle n = 1,2,... Integrale gibt angenommen, dass die Gewichtsfunktion p(x) überall im Intervall (a, b) definiert und positiv ist, mit der möglichen Ausnahme einer endlichen Anzahl von Punkten, an denen p(x) verschwinden kann. Nachdem wir die Differenzierung in Formel (3) durchgeführt haben, finden wir. Es kann gezeigt werden, dass die Chebyshev-Hermite-Polynome orthogonal auf dem Intervall Beispiel 4 sind. Das System der Bessel-Funktionen (jL(pix)^ ist orthogonal auf den Intervallnullstellen der Bessel-Funktion Beispiel 5. Betrachten Sie die Chebyshev-Hermite-Polynome, die lässt sich über die Gleichheit definieren. Es sei ein orthogonales System von Funktionen im Intervall (a, 6) und die Reihe (cj = const) konvergiere in diesem Intervall zur Funktion f(x): Multipliziert man beide Seiten der letzten Gleichung mit - fest) und integriert über x von a bis 6, erhält man aufgrund der Orthogonalität des Systems, dass diese Operation im Allgemeinen einen rein formalen Charakter hat. In manchen Fällen, beispielsweise wenn die Reihe (4) gleichmäßig konvergiert, alle Funktionen stetig sind und das Intervall (a, 6) endlich ist, ist diese Operation jedoch zulässig. Aber für uns ist jetzt die formale Interpretation wichtig. Es sei also eine Funktion gegeben. Bilden wir die Zahlen c* nach Formel (5) und schreiben wir die Reihe auf der rechten Seite als Fourier-Reihe der Funktion f(x) bezüglich des Systems (^n(i)). werden die Fourier-Koeffizienten der Funktion f(x) bezüglich dieses Systems genannt. Das Vorzeichen ~ in Formel (6) bedeutet nur, dass die Zahlen Cn durch Formel (5) mit der Funktion f(x) in Zusammenhang stehen (es wird nicht angenommen, dass die Reihe auf der rechten Seite überhaupt konvergiert, geschweige denn mit der Funktion f konvergiert). (X)). Daher stellt sich natürlich die Frage: Was sind die Eigenschaften dieser Serie? In welchem ​​Sinne „repräsentiert“ es die Funktion f(x)? 9.3. Konvergenz im Durchschnitt Definition. Eine Folge konvergiert im Mittel gegen das Element ], wenn die Norm im Raum liegt. Satz 6. Wenn eine Folge ) gleichmäßig konvergiert, dann konvergiert sie im Mittel. M Die Folge ()) konvergiere gleichmäßig auf dem Intervall [a, b] zur Funktion /(x). Das bedeutet, dass wir für alle, für alle hinreichend großen n, Also haben, woraus unsere Aussage folgt. Das Umgekehrte gilt nicht: Die Folge () kann im Mittel gegen /(x) konvergieren, aber nicht gleichmäßig konvergent sein. Beispiel. Betrachten Sie die Folge nx. Es ist leicht zu erkennen, dass diese Konvergenz jedoch nicht einheitlich ist: Es gibt beispielsweise e, so dass, egal wie groß n ist, auf dem Intervall Cosinus-Fourier-Reihen für eine Funktion mit einer beliebigen komplexen Darstellung der Fourier-Reihe Fourier-Reihe für allgemeine orthogonale Funktionssysteme Fourier-Reihe für ein orthogonales System Minimale Eigenschaft der Fourier-Koeffizienten Besselsche Ungleichung Parsevalsche Gleichheit Geschlossene Systeme Vollständigkeit und Geschlossenheit von Systemen und Wir bezeichnen mit c* die Fourier-Koeffizienten der Funktion /(x ) durch ein Orthonormalsystem b Betrachten Sie eine lineare Kombination, bei der n ^ 1 eine feste ganze Zahl ist, und ermitteln Sie die Werte der Konstanten, bei denen das Integral einen Minimalwert annimmt. Schreiben wir es detaillierter. Aufgrund der Orthonormalität des Systems erhalten wir, dass die ersten beiden Terme auf der rechten Seite der Gleichheit (7) unabhängig sind und der dritte Term nicht negativ ist. Daher nimmt das Integral (*) bei ak = sk einen Minimalwert an. Das Integral wird als mittlere quadratische Näherung der Funktion /(x) durch eine Linearkombination von Tn(x) bezeichnet. Somit nimmt die quadratische Mittelwertnäherung der Funktion /\ einen minimalen Wert an, wenn. wenn Tn(x) die 71. Teilsumme der Fourier-Reihe der Funktion /(x) über dem System ( ist. Mit ak = sk erhalten wir aus (7) Gleichheit (9), die als Bessel-Identität bezeichnet wird. Da sie links ist Seite ist nicht negativ, dann folgt daraus die Besselsche Ungleichung. Da ich hier willkürlich bin, kann die Besselsche Ungleichung in einer verstärkten Form dargestellt werden, d. h. für jede Funktion (die Reihe quadrierter Fourier-Koeffizienten dieser Funktion in einem Orthonormalsystem) konvergiert . Da das System im Intervall [-x, m] orthonormal ist, ergibt die Ungleichung (10), übersetzt in die übliche Notation der trigonometrischen Fourier-Reihe, die Beziehung do, die für jede Funktion /(x) mit einem integrierbaren Quadrat gilt. Wenn f2(x) integrierbar ist, dann erhalten wir aufgrund der notwendigen Bedingung für die Konvergenz der Reihe auf der linken Seite der Ungleichung (11) dies. Parsevals Gleichheit Für einige Systeme (^„(x)) kann das Ungleichheitszeichen in Formel (10) (für alle Funktionen f(x) 6 ×) durch ein Gleichheitszeichen ersetzt werden. Die resultierende Gleichheit wird Parseval-Steteklov-Gleichheit (Vollständigkeitsbedingung) genannt. Die Besselsche Identität (9) ermöglicht es uns, Bedingung (12) in einer äquivalenten Form zu schreiben. Die Erfüllung der Vollständigkeitsbedingung bedeutet also, dass die Teilsummen Sn(x) der Fourier-Reihe der Funktion /(x) gegen die Funktion konvergieren /(x) im Durchschnitt, d.h. gemäß der Raumnorm 6]. Definition. Ein Orthonormalsystem ( heißt vollständig in b2[ày b], wenn jede Funktion im Durchschnitt mit beliebiger Genauigkeit durch eine Linearkombination der Form mit einer ausreichend großen Anzahl von Termen angenähert werden kann, d. h. wenn für jede Funktion /(x) ∈ b2 [a, b\ und für jedes e > 0 gibt es eine natürliche Zahl nq und Zahlen a\, a2y..., so dass Nein. Aus der obigen Argumentation folgt Satz 7. Wenn durch Orthonormalisierung das System ) im Raum vollständig ist, ist das Die Fourier-Reihe jeder Funktion / in diesem System konvergiert im Durchschnitt, d. h. gemäß der Norm. Es kann gezeigt werden, dass das trigonometrische System im Raum vollständig ist. Satz 8. Wenn eine Funktion /o ist, konvergiert ihre trigonometrische Fourier-Reihe im Durchschnitt gegen sie. 9.5. Geschlossene Systeme. Vollständigkeit und Geschlossenheit von Systemen Definition. Ein orthonormales Funktionensystem heißt geschlossen, wenn es im Raum Li\a, b) keine zu allen Funktionen orthogonale Funktion ungleich Null gibt. Im Raum L2\a, b\ stimmen die Konzepte der Vollständigkeit und der Abgeschlossenheit orthonormaler Systeme überein. Übungen 1. Erweitern Sie die Funktion 2 zu einer Fourier-Reihe im Intervall (-i-, x) 2. Erweitern Sie die Funktion zu einer Fourier-Reihe im Intervall (-tr, tr) 3. Erweitern Sie die Funktion 4 zu einer Fourier-Reihe in das Intervall (-tr, tr) in die Fourier-Reihe im Intervall (-jt, tr) Funktion 5. Erweitern Sie die Funktion f(x) = x + x zu einer Fourier-Reihe im Intervall (-tr, tr). 6. Erweitern Sie die Funktion n zu einer Fourier-Reihe im Intervall (-jt, tr) 7. Erweitern Sie die Funktion /(x) = sin2 x zu einer Fourier-Reihe im Intervall (-tr, x). 8. Erweitern Sie die Funktion f(x) = y zu einer Fourier-Reihe im Intervall (-tr, jt). 9. Erweitern Sie die Funktion f(x) = | Sünde x|. 10. Erweitern Sie die Funktion f(x) = § zu einer Fourier-Reihe im Intervall (-π-, π). 11. Erweitern Sie die Funktion f(x) = sin § zu einer Fourier-Reihe im Intervall (-tr, tr). 12. Erweitern Sie die Funktion f(x) = n -2x, gegeben im Intervall (0, x), zu einer Fourier-Reihe und erweitern Sie sie in das Intervall (-x, 0): a) auf gerade Weise; b) auf seltsame Weise. 13. Erweitern Sie die Funktion /(x) = x2, gegeben im Intervall (0, x), in eine Fourier-Reihe in Sinuswerten. 14. Erweitern Sie die Funktion /(x) = 3, gegeben im Intervall (-2,2), in eine Fourier-Reihe. 15. Erweitern Sie die Funktion f(x) = |x|, gegeben im Intervall (-1,1), in eine Fourier-Reihe. 16. Erweitern Sie die im Intervall (0,1) angegebene Funktion f(x) = 2x zu einer Fourier-Reihe in Sinuswerten.

Ministerium für allgemeine und berufliche Bildung

Staatliche Universität für Tourismus Sotschi

und Resort-Geschäft

Pädagogisches Institut

Fakultät für Mathematik

Abteilung für Allgemeine Mathematik

DIPLOMARBEIT

Fourierreihen und ihre Anwendungen

In der mathematischen Physik.

Abgeschlossen von: Student im 5. Jahr

Vollzeitstudienunterschrift

Spezialität 010100

"Mathematik"

Kasperova N.S.

Studierendenausweis-Nr. 95471

Wissenschaftlicher Betreuer: außerordentlicher Professor, Kandidat.

technische Signatur Wissenschaften

Pozin P.A.

Sotschi, 2000

1. Einleitung.

2. Das Konzept einer Fourier-Reihe.

2.1. Bestimmung von Fourier-Reihenkoeffizienten.

2.2. Integrale periodischer Funktionen.

3. Konvergenzzeichen von Fourier-Reihen.

3.1. Beispiele für die Entwicklung von Funktionen in Fourier-Reihen.

4. Eine Anmerkung zur Fourier-Reihenentwicklung einer periodischen Funktion

5. Fourier-Reihe für gerade und ungerade Funktionen.

6. Fourier-Reihe für Funktionen mit Periode 2 l .

7. Fourier-Reihenentwicklung einer nichtperiodischen Funktion.

Einführung.

Jean Baptiste Joseph Fourier – französischer Mathematiker, Mitglied der Pariser Akademie der Wissenschaften (1817).

Fouriers erste Arbeiten bezogen sich auf Algebra. Bereits in Vorlesungen von 1796 stellte er einen nach ihm benannten Satz über die Anzahl der zwischen gegebenen Grenzen liegenden reellen Wurzeln einer algebraischen Gleichung vor (veröffentlicht 1820); Eine vollständige Lösung für die Anzahl der reellen Wurzeln einer algebraischen Gleichung wurde 1829 von J.S.F. erhalten. Durch Körperverletzung. Im Jahr 1818 untersuchte Fourier die Frage nach den Bedingungen für die Anwendbarkeit der von Newton entwickelten Methode der numerischen Lösung von Gleichungen, ohne von ähnlichen Ergebnissen zu wissen, die der französische Mathematiker J.R. 1768 erzielte. Murailem. Das Ergebnis von Fouriers Arbeit über numerische Methoden zur Lösung von Gleichungen ist „Analysis of Definite Equations“, das 1831 posthum veröffentlicht wurde.

Fouriers Hauptstudiengebiet war die mathematische Physik. In den Jahren 1807 und 1811 präsentierte er der Pariser Akademie der Wissenschaften seine ersten Entdeckungen zur Theorie der Wärmeausbreitung in Festkörpern und veröffentlichte 1822 das berühmte Werk „Analytische Theorie der Wärme“, das eine wichtige Rolle in der weiteren Geschichte von Feststoffen spielte Mathematik. Dies ist die mathematische Theorie der Wärmeleitfähigkeit. Aufgrund der Allgemeingültigkeit der Methode wurde dieses Buch zur Quelle aller modernen Methoden der mathematischen Physik. In dieser Arbeit leitete Fourier die Differentialgleichung der Wärmeleitfähigkeit ab und entwickelte die zuvor von D. Bernoulli dargelegten Ideen weiter. Er entwickelte eine Methode zur Trennung von Variablen (Fourier-Methode), um die Wärmeleitungsgleichung unter bestimmten gegebenen Randbedingungen zu lösen, die er auf a anwendete Anzahl der Sonderfälle (Würfel, Zylinder usw.). Diese Methode basiert auf der Darstellung von Funktionen durch trigonometrische Fourier-Reihen.

Fourier-Reihen sind mittlerweile zu einem gut entwickelten Werkzeug in der Theorie partieller Differentialgleichungen zur Lösung von Randwertproblemen geworden.

1. Das Konzept einer Fourier-Reihe.(S. 94, Uvarenkov)

Fourier-Reihen spielen eine wichtige Rolle in der mathematischen Physik, der Elastizitätstheorie, der Elektrotechnik und insbesondere in ihrem Sonderfall – der trigonometrischen Fourier-Reihe.

Eine trigonometrische Reihe ist eine Reihe der Form

oder symbolisch:

wobei ω, a 0, a 1, …, a n, …, b 0, b 1, …, b n, … konstante Zahlen sind (ω>0).

Einige Probleme der Physik haben in der Vergangenheit zur Untersuchung solcher Reihen geführt, beispielsweise das Problem der Saitenschwingungen (18. Jahrhundert), das Problem der Gesetzmäßigkeiten in den Phänomenen der Wärmeleitung usw. In Anwendungen die Betrachtung trigonometrischer Reihen , ist in erster Linie mit der Aufgabe verbunden, eine gegebene Bewegung, beschrieben durch die Gleichung y = ƒ(χ), in darzustellen

Somit kommen wir zu folgendem Problem: Finden Sie heraus, ob es für eine gegebene Funktion ƒ(x) in einem gegebenen Intervall eine Reihe (1) gibt, die in diesem Intervall zu dieser Funktion konvergieren würde. Wenn dies möglich ist, dann sagt man, dass die Funktion ƒ(x) in diesem Intervall zu einer trigonometrischen Reihe entwickelt wird.

Die Reihe (1) konvergiert aufgrund der Periodizität der Funktionen irgendwann x 0

und deshalb

2. Bestimmung von Reihenkoeffizienten mittels Fourier-Formeln.

Eine periodische Funktion ƒ(x) mit der Periode 2π sei so, dass sie durch eine trigonometrische Reihe dargestellt wird, die im Intervall (-π, π) gegen eine gegebene Funktion konvergiert, d. h. sie ist die Summe dieser Reihe:

Nehmen wir an, dass das Integral der Funktion auf der linken Seite dieser Gleichheit gleich der Summe der Integrale der Terme dieser Reihe ist. Dies gilt, wenn wir annehmen, dass die Zahlenreihe, die aus den Koeffizienten einer gegebenen trigonometrischen Reihe besteht, absolut konvergent ist, d. h. die positive Zahlenreihe konvergiert

Die Reihe (1) ist Majorisierbar und kann Term für Term im Intervall (-π, π) integriert werden. Integrieren wir beide Seiten der Gleichheit (2):

Lassen Sie uns jedes auf der rechten Seite erscheinende Integral separat auswerten:

Auf diese Weise,

Schätzung von Fourier-Koeffizienten.(Bugrow)

Satz 1. Die Funktion ƒ(x) der Periode 2π habe eine stetige Ableitung ƒ ( s) (x) Ordnung s, die die Ungleichung auf der gesamten reellen Achse erfüllt:

│ ƒ (s) (x)│≤ M s ; (5)

dann die Fourier-Koeffizienten der Funktion ƒ die Ungleichung erfüllen

Nachweisen. Teilweise integrieren und berücksichtigen

ƒ(-π) = ƒ(π), wir haben

Integrieren Sie die rechte Seite von (7) sequentiell unter Berücksichtigung der Tatsache, dass die Ableitungen ƒ ΄, …, ƒ (s-1) stetig sind und an den Punkten t = -π und t = π die gleichen Werte annehmen Neben der Schätzung (5) erhalten wir die erste Schätzung (6).

Die zweite Schätzung (6) wird auf ähnliche Weise erhalten.

Satz 2. Für die Fourier-Koeffizienten ƒ(x) gilt folgende Ungleichung:

Nachweisen. Wir haben