Irregularly shaped trapezoid. Rectangular and isosceles trapezoid: properties and characteristics
\[(\Large(\text(Free trapezoid)))\]
Definitions
A trapezoid is a convex quadrilateral in which two sides are parallel and the other two sides are not parallel.
The parallel sides of a trapezoid are called its bases, and the other two sides are called its lateral sides.
The height of a trapezoid is the perpendicular drawn from any point of one base to another base.
Theorems: properties of a trapezoid
1) The sum of the angles at the side is \(180^\circ\) .
2) The diagonals divide the trapezoid into four triangles, two of which are similar, and the other two are equal in size.
Proof
1) Because \(AD\parallel BC\), then the angles \(\angle BAD\) and \(\angle ABC\) are one-sided for these lines and the transversal \(AB\), therefore, \(\angle BAD +\angle ABC=180^\circ\).
2) Because \(AD\parallel BC\) and \(BD\) are a secant, then \(\angle DBC=\angle BDA\) lie crosswise.
Also \(\angle BOC=\angle AOD\) as vertical.
Therefore, at two angles \(\triangle BOC \sim \triangle AOD\).
Let's prove that \(S_(\triangle AOB)=S_(\triangle COD)\). Let \(h\) be the height of the trapezoid. Then \(S_(\triangle ABD)=\frac12\cdot h\cdot AD=S_(\triangle ACD)\). Then: \
Definition
The midline of a trapezoid is a segment connecting the midpoints of the sides.
Theorem
The midline of the trapezoid is parallel to the bases and equal to their half-sum.

Proof*
1) Let's prove parallelism.

Let us draw through the point \(M\) the straight line \(MN"\parallel AD\) (\(N"\in CD\) ). Then, according to Thales’ theorem (since \(MN"\parallel AD\parallel BC, AM=MB\)) point \(N"\) is the middle of the segment \(CD\). This means that the points \(N\) and \(N"\) will coincide.
2) Let's prove the formula.
Let's do \(BB"\perp AD, CC"\perp AD\) . Let \(BB"\cap MN=M", CC"\cap MN=N"\).

Then, by Thales' theorem, \(M"\) and \(N"\) are the midpoints of the segments \(BB"\) and \(CC"\), respectively. This means that \(MM"\) is the middle line of \(\triangle ABB"\) , \(NN"\) is the middle line of \(\triangle DCC"\) . That's why: \
Because \(MN\parallel AD\parallel BC\) and \(BB", CC"\perp AD\), then \(B"M"N"C"\) and \(BM"N"C\) are rectangles. According to Thales' theorem, from \(MN\parallel AD\) and \(AM=MB\) it follows that \(B"M"=M"B\) . Hence, \(B"M"N"C"\) and \(BM"N"C\) are equal rectangles, therefore, \(M"N"=B"C"=BC\) .
Thus:
\ \[=\dfrac12 \left(AB"+B"C"+BC+C"D\right)=\dfrac12\left(AD+BC\right)\]
Theorem: property of an arbitrary trapezoid
The midpoints of the bases, the point of intersection of the diagonals of the trapezoid and the point of intersection of the extensions of the lateral sides lie on the same straight line.

Proof*
It is recommended that you familiarize yourself with the proof after studying the topic “Similarity of triangles”.
1) Let us prove that the points \(P\) , \(N\) and \(M\) lie on the same line.

Let's draw a straight line \(PN\) (\(P\) is the point of intersection of the extensions of the lateral sides, \(N\) is the middle of \(BC\)). Let it intersect the side \(AD\) at the point \(M\) . Let us prove that \(M\) is the midpoint of \(AD\) .
Consider \(\triangle BPN\) and \(\triangle APM\) . They are similar at two angles (\(\angle APM\) – general, \(\angle PAM=\angle PBN\) as corresponding at \(AD\parallel BC\) and \(AB\) secant). Means: \[\dfrac(BN)(AM)=\dfrac(PN)(PM)\]
Consider \(\triangle CPN\) and \(\triangle DPM\) . They are similar at two angles (\(\angle DPM\) – general, \(\angle PDM=\angle PCN\) as corresponding at \(AD\parallel BC\) and \(CD\) secant). Means: \[\dfrac(CN)(DM)=\dfrac(PN)(PM)\]
From here \(\dfrac(BN)(AM)=\dfrac(CN)(DM)\). But \(BN=NC\) therefore \(AM=DM\) .
2) Let us prove that the points \(N, O, M\) lie on the same line.

Let \(N\) be the midpoint of \(BC\) and \(O\) be the point of intersection of the diagonals. Let's draw a straight line \(NO\) , it will intersect the side \(AD\) at the point \(M\) . Let us prove that \(M\) is the midpoint of \(AD\) .
\(\triangle BNO\sim \triangle DMO\) along two angles (\(\angle OBN=\angle ODM\) lying crosswise at \(BC\parallel AD\) and \(BD\) secant; \(\angle BON=\angle DOM\) as vertical). Means: \[\dfrac(BN)(MD)=\dfrac(ON)(OM)\]
Likewise \(\triangle CON\sim \triangle AOM\). Means: \[\dfrac(CN)(MA)=\dfrac(ON)(OM)\]
From here \(\dfrac(BN)(MD)=\dfrac(CN)(MA)\). But \(BN=CN\) therefore \(AM=MD\) .
\[(\Large(\text(Isosceles trapezoid)))\]
Definitions
A trapezoid is called rectangular if one of its angles is right.
A trapezoid is called isosceles if its sides are equal.
Theorems: properties of an isosceles trapezoid
1) An isosceles trapezoid has equal base angles.
2) The diagonals of an isosceles trapezoid are equal.
3) Two triangles formed by diagonals and a base are isosceles.
Proof
1) Consider the isosceles trapezoid \(ABCD\) .

From the vertices \(B\) and \(C\), we drop the perpendiculars \(BM\) and \(CN\) to the side \(AD\), respectively. Since \(BM\perp AD\) and \(CN\perp AD\) , then \(BM\parallel CN\) ; \(AD\parallel BC\) , then \(MBCN\) is a parallelogram, therefore, \(BM = CN\) .
Consider the right triangles \(ABM\) and \(CDN\) . Since their hypotenuses are equal and the leg \(BM\) is equal to the leg \(CN\) , then these triangles are equal, therefore, \(\angle DAB = \angle CDA\) .
2) 
Because \(AB=CD, \angle A=\angle D, AD\)- general, then according to the first sign. Therefore, \(AC=BD\) .
3) Because \(\triangle ABD=\triangle ACD\), then \(\angle BDA=\angle CAD\) . Therefore, the triangle \(\triangle AOD\) is isosceles. Similarly, it is proved that \(\triangle BOC\) is isosceles.
Theorems: signs of an isosceles trapezoid
1) If a trapezoid has equal base angles, then it is isosceles.
2) If a trapezoid has equal diagonals, then it is isosceles.
Proof
Consider the trapezoid \(ABCD\) such that \(\angle A = \angle D\) .

Let's complete the trapezoid to the triangle \(AED\) as shown in the figure. Since \(\angle 1 = \angle 2\) , then the triangle \(AED\) is isosceles and \(AE = ED\) . Angles \(1\) and \(3\) are equal as corresponding angles for parallel lines \(AD\) and \(BC\) and secant \(AB\). Similarly, angles \(2\) and \(4\) are equal, but \(\angle 1 = \angle 2\), then \(\angle 3 = \angle 1 = \angle 2 = \angle 4\), therefore, the triangle \(BEC\) is also isosceles and \(BE = EC\) .
Eventually \(AB = AE - BE = DE - CE = CD\), that is, \(AB = CD\), which is what needed to be proven.
2) Let \(AC=BD\) . Because \(\triangle AOD\sim \triangle BOC\), then we denote their similarity coefficient as \(k\) . Then if \(BO=x\) , then \(OD=kx\) . Similar to \(CO=y \Rightarrow AO=ky\) .

Because \(AC=BD\) , then \(x+kx=y+ky \Rightarrow x=y\) . This means \(\triangle AOD\) is isosceles and \(\angle OAD=\angle ODA\) .
Thus, according to the first sign \(\triangle ABD=\triangle ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\)– general). So, \(AB=CD\) , why.
Circumscribed circle and trapezoid. Hello! There is one more publication for you, in which we will look at problems with trapezoids. The tasks are part of the mathematics exam. Here they are combined into a group; not just one trapezoid is given, but a combination of bodies - a trapezoid and a circle. Most of these problems are solved orally. But there are also those that need to be paid special attention to, for example, task 27926.
What theory do you need to remember? This:
Problems with trapezoids that are available on the blog can be viewed Here.
27924. A circle is described around a trapezoid. The perimeter of the trapezoid is 22, the midline is 5. Find the side of the trapezoid.

Note that a circle can only be described around an isosceles trapezoid. We are given the middle line, which means we can determine the sum of the bases, that is:
This means the sum of the sides will be equal to 22–10=12 (perimeter minus the base). Since the sides of an isosceles trapezoid are equal, one side will be equal to six.
27925. The lateral side of an isosceles trapezoid is equal to its smaller base, the angle at the base is 60 0, the larger base is 12. Find the circumradius of this trapezoid.

If you solved problems with a circle and a hexagon inscribed in it, then you will immediately voice the answer - the radius is 6. Why?
Look: an isosceles trapezoid with a base angle equal to 60 0 and equal sides AD, DC and CB, is half of a regular hexagon:

In such a hexagon, the segment connecting opposite vertices passes through the center of the circle. *The center of the hexagon and the center of the circle coincide, more details
That is, the larger base of this trapezoid coincides with the diameter of the circumscribed circle. So the radius is six.
*Of course, we can consider the equality of triangles ADO, DOC and OCB. Prove that they are equilateral. Next, conclude that angle AOB is equal to 180 0 and point O is equidistant from vertices A, D, C and B, and therefore AO=OB=12/2=6.
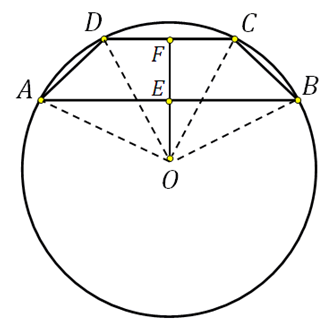
27926. The bases of an isosceles trapezoid are 8 and 6. The radius of the circumscribed circle is 5. Find the height of the trapezoid.

Note that the center of the circumscribed circle lies on the axis of symmetry, and if we construct the height of the trapezoid passing through this center, then when it intersects with the bases it will divide them in half. Let's show this in the sketch and also connect the center to the vertices:

The segment EF is the height of the trapezoid, we need to find it.
In right triangle OFC we know the hypotenuse (this is the radius of the circle), FC=3 (since DF=FC). Using the Pythagorean theorem we can calculate OF:

In the right triangle OEB, we know the hypotenuse (this is the radius of the circle), EB=4 (since AE=EB). Using the Pythagorean theorem we can calculate OE:

Thus EF=FO+OE=4+3=7.
Now an important nuance!
In this problem, the figure clearly shows that the bases lie on opposite sides of the center of the circle, so the problem is solved this way.
What if the conditions did not include a sketch?
Then the problem would have two answers. Why? Look carefully - two trapezoids with given bases can be inscribed in any circle:
*That is, given the bases of the trapezoid and the radius of the circle, there are two trapezoids.
And the solution to the “second option” will be as follows.
Using the Pythagorean theorem we calculate OF:
Let's also calculate OE:

Thus EF=FO–OE=4–3=1.
Of course, in a problem with a short answer on the Unified State Examination there cannot be two answers, and a similar problem will not be given without a sketch. Therefore, pay special attention to the sketch! Namely: how the bases of the trapezoid are located. But in tasks with a detailed answer, this was present in past years (with a slightly more complicated condition). Anyone who considered only one option for the location of the trapezoid lost a point on this task.
27937. A trapezoid is circumscribed around a circle, the perimeter of which is 40. Find its midline.

Here we should immediately recall the property of a quadrilateral circumscribed about a circle:
The sums of the opposite sides of any quadrilateral circumscribed about a circle are equal.
- (Greek trapezion). 1) in geometry, a quadrilateral in which two sides are parallel and two are not. 2) a figure adapted for gymnastic exercises. Dictionary of foreign words included in the Russian language. Chudinov A.N., 1910. TRAPEZE... ... Dictionary of foreign words of the Russian language
Trapezoid- Trapezoid. TRAPEZE (from the Greek trapezion, literally table), a convex quadrilateral in which two sides are parallel (the bases of the trapezoid). The area of a trapezoid is equal to the product of half the sum of the bases (midline) and the height. ... Illustrated Encyclopedic Dictionary
Quadrangle, projectile, crossbar Dictionary of Russian synonyms. trapezoid noun, number of synonyms: 3 crossbar (21) ... Synonym dictionary
- (from the Greek trapezion, literally table), a convex quadrangle in which two sides are parallel (the bases of a trapezoid). The area of a trapezoid is equal to the product of half the sum of the bases (midline) and the height... Modern encyclopedia
- (from the Greek trapezion, lit. table), a quadrilateral in which two opposite sides, called the bases of the trapezoid, are parallel (in the figure AD and BC), and the other two are non-parallel. The distance between the bases is called the height of the trapezoid (at ... ... Big Encyclopedic Dictionary
TRAPEZOUS, a quadrangular flat figure in which two opposite sides are parallel. The area of a trapezoid is equal to half the sum of the parallel sides multiplied by the length of the perpendicular between them... Scientific and technical encyclopedic dictionary
TRAPEZE, trapezoid, women's (from Greek trapeza table). 1. Quadrilateral with two parallel and two non-parallel sides (mat.). 2. A gymnastic apparatus consisting of a crossbar suspended on two ropes (sports). Acrobatic... ... Ushakov's Explanatory Dictionary
TRAPEZE, and, female. 1. A quadrilateral with two parallel and two non-parallel sides. The bases of the trapezoid (its parallel sides). 2. A circus or gymnastics apparatus is a crossbar suspended on two cables. Ozhegov's explanatory dictionary. WITH … Ozhegov's Explanatory Dictionary
Female, geom. a quadrilateral with unequal sides, two of which are parallel (parallel). Trapezoid, a similar quadrilateral in which all sides run apart. Trapezohedron, a body faceted by trapezoids. Dahl's Explanatory Dictionary. IN AND. Dahl. 1863 1866 … Dahl's Explanatory Dictionary
- (Trapeze), USA, 1956, 105 min. Melodrama. Aspiring acrobat Tino Orsini joins a circus troupe where Mike Ribble, a famous former trapeze artist, works. Mike once performed with Tino's father. Young Orsini wants Mike... Encyclopedia of Cinema
A quadrilateral in which two sides are parallel and the other two sides are not parallel. The distance between parallel sides is called. height T. If parallel sides and height contain a, b and h meters, then the area of T contains square meters ... Encyclopedia of Brockhaus and Efron
In the materials of various tests and exams, they are very often found trapezoid problems, the solution of which requires knowledge of its properties.
Let's find out what interesting and useful properties a trapezoid has for solving problems.
After studying the properties of the midline of a trapezoid, one can formulate and prove property of a segment connecting the midpoints of the diagonals of a trapezoid. The segment connecting the midpoints of the diagonals of a trapezoid is equal to half the difference of the bases.
MO is the middle line of triangle ABC and is equal to 1/2BC (Fig. 1).
MQ is the middle line of triangle ABD and is equal to 1/2AD.
Then OQ = MQ – MO, therefore OQ = 1/2AD – 1/2BC = 1/2(AD – BC).
When solving many problems on a trapezoid, one of the main techniques is to draw two heights in it.
Consider the following task.
Let BT be the height of an isosceles trapezoid ABCD with bases BC and AD, with BC = a, AD = b. Find the lengths of the segments AT and TD.
Solution.
Solving the problem is not difficult (Fig. 2), but it allows you to get property of the height of an isosceles trapezoid drawn from the vertex of an obtuse angle: the height of an isosceles trapezoid drawn from the vertex of an obtuse angle divides the larger base into two segments, the smaller of which is equal to half the difference of the bases, and the larger one is equal to half the sum of the bases.
When studying the properties of a trapezoid, you need to pay attention to such a property as similarity. So, for example, the diagonals of a trapezoid divide it into four triangles, and the triangles adjacent to the bases are similar, and the triangles adjacent to the sides are equal in size. This statement can be called property of triangles into which a trapezoid is divided by its diagonals. Moreover, the first part of the statement can be proven very easily through the sign of similarity of triangles at two angles. Let's prove second part of the statement.
Triangles BOC and COD have a common height (Fig. 3), if we take the segments BO and OD as their bases. Then S BOC /S COD = BO/OD = k. Therefore, S COD = 1/k · S BOC .
Similarly, triangles BOC and AOB have a common height if we take the segments CO and OA as their bases. Then S BOC /S AOB = CO/OA = k and S A O B = 1/k · S BOC .
From these two sentences it follows that S COD = S A O B.
Let's not dwell on the formulated statement, but find the relationship between the areas of the triangles into which the trapezoid is divided by its diagonals. To do this, let's solve the following problem.
Let point O be the intersection point of the diagonals of the trapezoid ABCD with the bases BC and AD. It is known that the areas of triangles BOC and AOD are equal to S 1 and S 2, respectively. Find the area of the trapezoid.
Since S COD = S A O B, then S ABC D = S 1 + S 2 + 2S COD.
From the similarity of triangles BOC and AOD it follows that BO/OD = √(S₁/S 2).
Therefore, S₁/S COD = BO/OD = √(S₁/S 2), which means S COD = √(S 1 · S 2).
Then S ABC D = S 1 + S 2 + 2√(S 1 · S 2) = (√S 1 + √S 2) 2.
Using similarity it is proved that property of a segment passing through the point of intersection of the diagonals of a trapezoid parallel to the bases.
Let's consider task:
Let point O be the intersection point of the diagonals of the trapezoid ABCD with the bases BC and AD. BC = a, AD = b. Find the length of the segment PK passing through the point of intersection of the diagonals of the trapezoid parallel to the bases. What segments is PK divided by point O (Fig. 4)?

From the similarity of triangles AOD and BOC it follows that AO/OC = AD/BC = b/a.
From the similarity of triangles AOP and ACB it follows that AO/AC = PO/BC = b/(a + b).
Hence PO = BC b / (a + b) = ab/(a + b).
Similarly, from the similarity of triangles DOK and DBC, it follows that OK = ab/(a + b).
Hence PO = OK and PK = 2ab/(a + b).
So, the proven property can be formulated as follows: a segment parallel to the bases of the trapezoid, passing through the point of intersection of the diagonals and connecting two points on the lateral sides, is divided in half by the point of intersection of the diagonals. Its length is the harmonic mean of the bases of the trapezoid.
Following four point property: in a trapezoid, the point of intersection of the diagonals, the point of intersection of the continuation of the sides, the midpoints of the bases of the trapezoid lie on the same line.
Triangles BSC and ASD are similar (Fig. 5) and in each of them the medians ST and SG divide the vertex angle S into equal parts. Therefore, points S, T and G lie on the same line.
In the same way, points T, O and G are located on the same line. This follows from the similarity of triangles BOC and AOD.
This means that all four points S, T, O and G lie on the same line.
You can also find the length of the segment dividing the trapezoid into two similar ones.
If trapezoids ALFD and LBCF are similar (Fig. 6), then a/LF = LF/b.
Hence LF = √(ab).
Thus, a segment dividing a trapezoid into two similar trapezoids has a length equal to the geometric mean of the lengths of the bases. 
Let's prove property of a segment dividing a trapezoid into two equal areas.
Let the area of the trapezoid be S (Fig. 7). h 1 and h 2 are parts of the height, and x is the length of the desired segment.
Then S/2 = h 1 (a + x)/2 = h 2 (b + x)/2 and
S = (h 1 + h 2) · (a + b)/2.
Let's create a system
(h 1 (a + x) = h 2 (b + x)
(h 1 · (a + x) = (h 1 + h 2) · (a + b)/2.
Solving this system, we obtain x = √(1/2(a 2 + b 2)).
Thus, the length of the segment dividing the trapezoid into two equal ones is equal to √((a 2 + b 2)/2)(mean square of base lengths).
So, for the trapezoid ABCD with bases AD and BC (BC = a, AD = b) we proved that the segment:
1) MN, connecting the midpoints of the lateral sides of the trapezoid, is parallel to the bases and equal to their half-sum (the arithmetic mean of the numbers a and b);
2) PK passing through the point of intersection of the diagonals of the trapezoid parallel to the bases is equal to
2ab/(a + b) (harmonic mean of numbers a and b);
3) LF, which splits a trapezoid into two similar trapezoids, has a length equal to the geometric mean of the numbers a and b, √(ab);
4) EH, dividing a trapezoid into two equal ones, has length √((a 2 + b 2)/2) (the root mean square of the numbers a and b).
Sign and property of an inscribed and circumscribed trapezoid.
Property of an inscribed trapezoid: a trapezoid can be inscribed in a circle if and only if it is isosceles.
Properties of the described trapezoid. A trapezoid can be described around a circle if and only if the sum of the lengths of the bases is equal to the sum of the lengths of the sides.
Useful consequences of the fact that a circle is inscribed in a trapezoid:
1. The height of the circumscribed trapezoid is equal to two radii of the inscribed circle.
2. The side of the described trapezoid is visible from the center of the inscribed circle at a right angle.
The first is obvious. To prove the second corollary, it is necessary to establish that the angle COD is right, which is also not difficult. But knowing this corollary allows you to use a right triangle when solving problems.
Let's specify corollaries for an isosceles circumscribed trapezoid:
The height of an isosceles circumscribed trapezoid is the geometric mean of the bases of the trapezoid
h = 2r = √(ab).
The considered properties will allow you to understand the trapezoid more deeply and ensure success in solving problems using its properties.
Still have questions? Don't know how to solve trapezoid problems?
To get help from a tutor -.
The first lesson is free!
blog.site, when copying material in full or in part, a link to the original source is required.
- The segment connecting the midpoints of the diagonals of a trapezoid is equal to half the difference of the bases
- Triangles formed by the bases of a trapezoid and the segments of the diagonals up to their point of intersection are similar
- Triangles formed by segments of the diagonals of a trapezoid, the sides of which lie on the lateral sides of the trapezoid - are equal in size (have the same area)
- If you extend the sides of the trapezoid towards the smaller base, then they will intersect at one point with the straight line connecting the midpoints of the bases
- A segment connecting the bases of a trapezoid and passing through the point of intersection of the diagonals of the trapezoid is divided by this point in a proportion equal to the ratio of the lengths of the bases of the trapezoid
- A segment parallel to the bases of the trapezoid and drawn through the point of intersection of the diagonals is divided in half by this point, and its length is equal to 2ab/(a + b), where a and b are the bases of the trapezoid
Properties of a segment connecting the midpoints of the diagonals of a trapezoid
Let's connect the midpoints of the diagonals of the trapezoid ABCD, as a result of which we will have a segment LM.
A segment connecting the midpoints of the diagonals of a trapezoid lies on the midline of the trapezoid.
This segment parallel to the bases of the trapezoid.
The length of the segment connecting the midpoints of the diagonals of a trapezoid is equal to half the difference of its bases.
LM = (AD - BC)/2
or
LM = (a-b)/2
Properties of triangles formed by the diagonals of a trapezoid

Triangles that are formed by the bases of a trapezoid and the point of intersection of the diagonals of the trapezoid - are similar.
Triangles BOC and AOD are similar. Since angles BOC and AOD are vertical, they are equal.
Angles OCB and OAD are internal angles lying crosswise with parallel lines AD and BC (the bases of the trapezoid are parallel to each other) and a secant line AC, therefore they are equal.
Angles OBC and ODA are equal for the same reason (internal crosswise).
Since all three angles of one triangle are equal to the corresponding angles of another triangle, then these triangles are similar.
What follows from this?
To solve problems in geometry, the similarity of triangles is used as follows. If we know the lengths of two corresponding elements of similar triangles, then we find the similarity coefficient (we divide one by the other). From where the lengths of all other elements are related to each other by exactly the same value.
Properties of triangles lying on the lateral side and diagonals of a trapezoid

Consider two triangles lying on the lateral sides of the trapezoid AB and CD. These are triangles AOB and COD. Despite the fact that the sizes of individual sides of these triangles may be completely different, but the areas of the triangles formed by the lateral sides and the point of intersection of the diagonals of the trapezoid are equal, that is, the triangles are equal in size.

If we extend the sides of the trapezoid towards the smaller base, then the point of intersection of the sides will be coincide with a straight line that passes through the middle of the bases.
Thus, any trapezoid can be expanded into a triangle. Wherein:
- Triangles formed by the bases of a trapezoid with a common vertex at the point of intersection of the extended sides are similar
- The straight line connecting the midpoints of the bases of the trapezoid is, at the same time, the median of the constructed triangle
Properties of a segment connecting the bases of a trapezoid

If you draw a segment whose ends lie on the bases of a trapezoid, which lies at the point of intersection of the diagonals of the trapezoid (KN), then the ratio of its constituent segments from the side of the base to the point of intersection of the diagonals (KO/ON) will be equal to the ratio of the bases of the trapezoid(BC/AD).
KO/ON = BC/AD
This property follows from the similarity of the corresponding triangles (see above).
Properties of a segment parallel to the bases of a trapezoid

If we draw a segment parallel to the bases of the trapezoid and passing through the point of intersection of the trapezoid’s diagonals, then it will have the following properties:
- Specified distance (KM) bisected by the intersection point of the trapezoid's diagonals
- Section length passing through the point of intersection of the diagonals of the trapezoid and parallel to the bases is equal to KM = 2ab/(a + b)
Formulas for finding the diagonals of a trapezoid

a, b- trapezoid bases
c,d- sides of the trapezoid
d1 d2- diagonals of a trapezoid
α β - angles with a larger base of the trapezoid
Formulas for finding the diagonals of a trapezoid through the bases, sides and angles at the base

The first group of formulas (1-3) reflects one of the main properties of trapezoid diagonals:
1. The sum of the squares of the diagonals of a trapezoid is equal to the sum of the squares of the sides plus twice the product of its bases. This property of trapezoid diagonals can be proven as a separate theorem
2 . This formula is obtained by transforming the previous formula. The square of the second diagonal is thrown through the equal sign, after which the square root is extracted from the left and right sides of the expression.
3 . This formula for finding the length of the diagonal of a trapezoid is similar to the previous one, with the difference that another diagonal is left on the left side of the expression
The next group of formulas (4-5) are similar in meaning and express a similar relationship.
The group of formulas (6-7) allows you to find the diagonal of a trapezoid if the larger base of the trapezoid, one side side and the angle at the base are known.
Formulas for finding the diagonals of a trapezoid through height

Task.
The diagonals of the trapezoid ABCD (AD | | BC) intersect at point O. Find the length of the base BC of the trapezoid if the base AD = 24 cm, length AO = 9 cm, length OS = 6 cm.
Solution.
The solution to this problem is ideologically absolutely identical to the previous problems.
Triangles AOD and BOC are similar in three angles - AOD and BOC are vertical, and the remaining angles are pairwise equal, since they are formed by the intersection of one line and two parallel lines.
Since the triangles are similar, all their geometric dimensions are related to each other, just like the geometric dimensions of the segments AO and OC known to us according to the conditions of the problem. That is
AO/OC = AD/BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Answer: 16 cm
Task .
In the trapezoid ABCD it is known that AD=24, BC=8, AC=13, BD=5√17. Find the area of the trapezoid. 
Solution .
To find the height of a trapezoid from the vertices of the smaller base B and C, we lower two heights to the larger base. Since the trapezoid is unequal, we denote the length AM = a, length KD = b ( not to be confused with the notation in the formula finding the area of a trapezoid). Since the bases of the trapezoid are parallel, and we dropped two heights perpendicular to the larger base, then MBCK is a rectangle.
Means
AD = AM+BC+KD
a + 8 + b = 24
a = 16 - b
Triangles DBM and ACK are rectangular, so their right angles are formed by the altitudes of the trapezoid. Let us denote the height of the trapezoid by h. Then, by the Pythagorean theorem
H 2 + (24 - a) 2 = (5√17) 2
And
h 2 + (24 - b) 2 = 13 2
Let's take into account that a = 16 - b, then in the first equation
h 2 + (24 - 16 + b) 2 = 425
h 2 = 425 - (8 + b) 2
Let's substitute the value of the square of the height into the second equation obtained using the Pythagorean Theorem. We get:
425 - (8 + b) 2 + (24 - b) 2 = 169
-(64 + 16b + b) 2 + (24 - b) 2 = -256
-64 - 16b - b 2 + 576 - 48b + b 2 = -256
-64b = -768
b = 12
So KD = 12
Where
h 2 = 425 - (8 + b) 2 = 425 - (8 + 12) 2 = 25
h = 5
Find the area of the trapezoid through its height and half the sum of the bases
, where a b - the base of the trapezoid, h - the height of the trapezoid
S = (24 + 8) * 5 / 2 = 80 cm 2
Answer: the area of the trapezoid is 80 cm2.




