Электрическое поле однородно заряженной плоскости. Применение теоремы Гаусса для расчета поля бесконечной равномерно заряженной плоскости

Ранее мы показали, что электрическое поле, создаваемое бесконечной равномерно заряженной пластиной является однородным, то есть напряженность поля одинакова во всех точках, причем вектор напряженности направлен перпендикулярно плоскости, а его модуль равен E o = σ/(2ε o) . Семейством силовых линий такого поля явяется набор параллельных прямых, перпендикулярных пластине. На рис. 275, 276 так же изображен график зависимости проекции вектора напряженности поля E z на ось Z перпендикулярную пластине (начало отсчета этой оси расположим на пластине). Понятно, что потенциал данного поля зависит только от координаты z , то есть эквипотенциальные поверхности в данном случае являются плоскостями, параллельными заряженной пластине.



рис. 275



рис. 276
 При традиционном выборе нулевого уровня потенциала φ(z → ∞) , потенциал произвольной точки равен работе по перемещению единичного положительного заряда из данной точки на бесконечность. Так как модуль напряженности постоянен, то такая работа (а, следовательно, и потенциал) оказывается равной бесконечности! Следовательно, указанный выбор нулевого уровня потенциала в данном случае непригоден.
 Поэтому следует воспользоваться произволом выбора нулевого уровня. Достаточно выбрать произвольную точку с координатой z = z o , и приписать ей произвольное значение потенциала φ(z o) = φ o (рис. 277).

рис. 277
 Теперь, чтобы вычислить значение потенциала в произвольной точке φ(z) , можно воспользоваться соотношением между напряженностью и потенциалом поля

 Учитывая, что в данном случае напряженность поля постоянна (при z > 0 ) это выражение записывается в виде

из которого следует искомая зависимость потенциала от координаты (при z > 0 )

 В частности, можно задать произвольное значение потенциала самой пластины, то есть положить при z = z o = 0, φ = φ o . Тогда значение потенциала в произвольной точке определяется функцией

график которой показан на рисунке 278.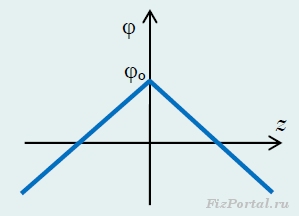

рис. 278
 То, что потенциал относительно бесконечности оказался бесконечно большим, вполне очевидно − ведь и бесконечная пластина обладает бесконечно большим зарядом. Как мы уже подчеркивали, такая система является идеализацией − бесконечных пластин не существует. В реальности все тела имеют конечные размеры, поэтому для них традиционный выбор нулевого потенциала возможен, правда в этом случае распределение поля может быть очень сложным. В рамках же рассматриваемой идеализации удобнее воспользоваться использованным нами выбором нулевого уровня.

Найдем распределение потенциала поля, создаваемого двумя одинаковыми равномерно заряженными параллельными пластинами, заряды которых равны по модулю и противоположны по знаку 1 (рис. 279).

Рис. 279
 Обозначим поверхностную плотность заряда на одной пластине +σ , а на другой −σ . Расстояние между пластинами h будем считать значительно меньшим размеров пластин. Введем систему координат, ось z которой перпендикулярна пластинам, начало координат разместим по средине между пластинами. Очевидно, для бесконечно больших пластин все характеристики поля (напряженность и потенциал) зависят только от координаты z . Для расчета напряженности поля в различных точках пространства воспользуемся полученным выражением для напряженности поля, создаваемого бесконечной равномерно заряженной пластиной и принципом суперпозиции.
Каждая равномерно заряженная пластина создает однородное поле, модуль напряженности которого равен E o = σ/(2ε o) , а направления указаны на рисунке 280, 281.



рис. 280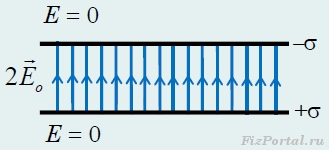

рис. 281
 Складывая напряженности полей по принципу суперпозиции, получим, что в пространстве между пластинами напряженность поля E = 2E o = σ/ε o вдвое превышает напряженность поля одной пластины (здесь поля отдельных пластин параллельны), а вне пластин поле отсутствует (здесь поля отдельных пластин противоположны).
 Строго говоря, для пластин конечных размеров поле не является однородным, силовые линии поля пластин конечных размеров показаны на рисунке 282.



рис. 282
 Наиболее сильные отклонения от однородности наблюдаются вблизи краев пластин (часто эти отклонения называют краевыми эффектами ). Однако, в области прилегающей к середине пластин поле с высокой степенью точности можно считать однородным, то есть в этой области можно пренебречь краевыми эффектами. Заметим, что погрешности такого приближения тем меньше, чем меньше отношение расстояния между пластинами к их размерам.
 Для однозначного определения распределения потенциала поля, необходимо выбрать уровень нулевого потенциала. Будем считать, что потенциал равным нулю в плоскости расположенной по средине между пластинами, то есть, положим φ = 0 при z = 0 .
 Не смотря на произвол в выборе нулевого уровня потенциала, наш выбор может быть логически обоснован на основании симметрии системы. Действительно, рассматриваемая система зарядов зеркально повторяет себя при зеркальном отражении относительно плоскости z = 0 и одновременном изменении знаков зарядов. Поэтому желательно, чтобы и распределение потенциала обладало такой же симметрией: восстанавливалось при зеркальном отражении с одновременным изменением знака всех функций поля. Выбранный нами способ выбора нулевого потенциала удовлетворяет такой симметрии.



рис. 283
 Обозначим потенциал положительно заряженной пластины +φ o , тогда потенциал отрицательно заряженной пластины будет равен φ o . Эти потенциалы легко определить, используя найденное значение напряженности поля между пластинами и связь между напряженностью и разностью потенциалов электрического поля. Уравнение этой связи в данном случае имеет вид +φo − φ o = Eh . Из этого соотношения определяем значения потенциалов пластин φ o = σh/(2ε o) . Учитывая, что между пластинами поле однородное (поэтому потенциал изменяется линейно), а вне пластин поле отсутствует (поэтому здесь потенциал постоянен), зависимость потенциала от координаты z имеет вид (рис. 284)

рис. 284

 Задания для самостоятельной работы.
 1. Во всех рассмотренных примерах проделайте обратную операцию: по найденному распределению потенциала с помощью формулы E x = −Δφ/Δx рассчитайте напряженности рассмотренных полей.
 2. Строго выведите формулу (6).
 3. Качественно объясните следующий «парадокс». В поле плоского конденсатора неоднозначно определен потенциал «бесконечности»: при движении в положительном направлении оси Z потенциал «бесконечности» оказался равным −φ o ; при движении в отрицательном направлении оси Z − +φ o , при движении вдоль осей X или Y − равен нулю. Так чему равен потенциал «бесконечности» в реальной системе двух пластин конечных размеров?

1 Такая система называется плоским конденсатором, подробнее эти устройства мы будем изучать позже.

Будем считать заряд положительным. Плоскость заряжена с постоянной поверхностной плотностью . Из симметрии вытекает, что напряженность в любой точке поля имеет направление, перпендикулярное к плоскости (рис. 2.10). Очевидно, что в симметричных относительно плоскости точках напряженность поля одинакова по величине и противоположна по направлению.

Выделим на заряженной плоскости площадку . Окружим эту площадку замкнутой поверхностью. В качестве замкнутой поверхности представим цилиндрическую поверхность с образующими, перпендикулярными к плоскости и основаниями величины , расположенными относительно плоскости симметрично. Применим к этой поверхности теорему Гаусса . Поток через боковую часть поверхности будет отсутствовать, так как в каждой ее точке равна нулю. Для оснований совпадает с . Следовательно, суммарный поток через поверхность будет равен . Внутри поверхности заключен заряд . Согласно теореме Гаусса, должно выполняться условие: , откуда . (3)

Полученный результат не зависит от длины цилиндра, т.е. на любых расстояниях от плоскости напряженность поля одинакова по величине. Картина линий напряженности выглядит, как показано на рис. 2.11. Для отрицательно заряженной плоскости направления векторов изменятся на обратные. Если плоскость конечных размеров, то полученный результат будет справедлив лишь для точек, расстояние которых от края пластины значительно превышает расстояние от самой пластинки (рис. 2.12).