Електрическо поле на равномерно заредена равнина. Приложение на теоремата на Гаус за изчисляване на полето на безкрайна равномерно заредена равнина

По-рано го показахме електрическо поле, създадена от безкрайна равномерно заредена плоча, е хомогенна, т.е. силата на полето е еднаква във всички точки, а векторът на интензитета е насочен перпендикулярно на равнината и неговият модул е ​​равен на E o = σ/(2ε o). Семейството от силови линии на такова поле е набор от успоредни линии, перпендикулярни на плочата. На фиг. 275, 276 също показва графика на проекцията на вектора на силата на полето Езна ос Зперпендикулярна на плочата (ще поставим началото на тази ос върху плочата). Ясно е, че потенциалът на това поле зависи само от координатата z, тоест еквипотенциалните повърхности в този случай са равнини, успоредни на заредената плоча.



ориз. 275



ориз. 276
С традиционния избор на ниво на нулев потенциал φ(z → ∞), потенциалът на произволна точка е равен на работата по преместване на единица положителен заряд от дадена точка до безкрайност. Тъй като модулът на напрежението е постоянен, такава работа (и следователно потенциал) се оказва равна на безкрайност! Следователно посоченият избор на ниво на нулев потенциал е неподходящ в този случай.
Следователно трябва да се възползвате от произвола при избора на нулевото ниво. Достатъчно е да изберете произволна точка с координата z = z oи му присвоете произволна потенциална стойност φ(z o) = φ o(фиг. 277).

ориз. 277
Сега, за да изчислим потенциалната стойност в произволна точка φ(z), можете да използвате връзката между силата на полето и потенциала

Като се има предвид, че в този случай напрегнатостта на полето е постоянна (при z > 0) този израз е записан във формата

от което следва желаната зависимост на потенциала от координатата (при z > 0)

По-специално, можете да зададете произволна стойност на потенциала на самата плоча, т.е z = z o = 0, φ = φ o. Тогава стойността на потенциала в произволна точка се определя от функцията

чиято графика е показана на фигура 278.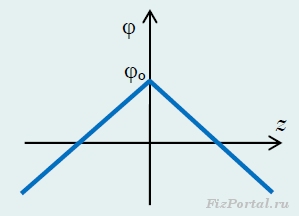

ориз. 278
Фактът, че потенциалът спрямо безкрайността се оказа безкрайно голям, е съвсем очевиден - в крайна сметка една безкрайна плоча също има безкрайно голям заряд. Както вече подчертахме, такава система е идеализация – безкрайни плочи не съществуват. В действителност всички тела имат крайни размери, така че за тях е възможен традиционният избор на нулев потенциал, въпреки че в този случай разпределението на полето може да бъде много сложно. В рамките на разглежданата идеализация е по-удобно да се използва изборът на нулевото ниво, който използвахме.

Нека намерим разпределението на потенциала на полето, създадено от две еднакви равномерно заредени успоредни плочи, чиито заряди са равни по големина и противоположни по знак 1 (фиг. 279).

Ориз. 279
Нека обозначим повърхностната плътност на заряда на една плоча +σ , а от другата −σ . Разстояние между плочите чще приемем, че е значително по-малък от размера на плочите. Нека въведем координатна система, ос zкойто е перпендикулярен на плочите, началото на координатите ще бъде поставено в средата между плочите. Очевидно за безкрайно големи плочи всички характеристики на полето (сила и потенциал) зависят само от координатата z. За да изчислим силата на полето в различни точки в пространството, ще използваме получения израз за силата на полето, създадена от безкрайна равномерно заредена плоча и принципа на суперпозицията.
Всяка еднакво заредена плоча създава еднородно поле, чийто модул е ​​равен на E o = σ/(2ε o), а посоките са посочени на Фигура 280, 281.



ориз. 280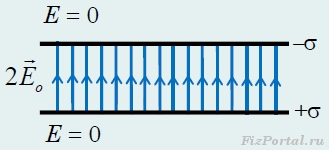

ориз. 281
Като добавим напрегнатостта на полето по принципа на суперпозицията, получаваме, че в пространството между плочите напрегнатостта на полето E = 2E o = σ/ε oдва пъти силата на полето на една плоча (тук полетата на отделните плочи са успоредни), и няма поле извън плочите (тук полетата на отделните плочи са срещуположни).
Строго погледнато, за плочи с крайни размери полето не е равномерно; силовите линии на плочите с крайни размери са показани на фигура 282.



ориз. 282
Най-силните отклонения от хомогенността се наблюдават в близост до краищата на плочите (често тези отклонения се наричат ръбови ефекти). Въпреки това, в областта, съседна на средата на плочите, полето може да се счита за хомогенно с висока степен на точност, тоест в тази област ръбовите ефекти могат да бъдат пренебрегнати. Имайте предвид, че колкото по-малко е отношението на разстоянието между плочите към техните размери, толкова по-малки са грешките в това приближение.
За да се определи недвусмислено разпределението на потенциала на полето, е необходимо да се избере нивото на нулев потенциал. Ще приемем, че потенциалът е равен на нула в равнината, разположена в средата между плочите, тоест поставяме φ = 0 при z = 0.
Въпреки произволността при избора на ниво на нулев потенциал, нашият избор може да бъде логически обоснован въз основа на симетрията на системата. Всъщност разглежданата система от заряди се повтаря в огледално отражение спрямо равнината z = 0и едновременна промяна на знаците на зарядите. Следователно е желателно разпределението на потенциала да има същата симетрия: то се възстановява при огледално отражение с едновременна промяна на знака на всички функции на полето. Методът, който сме избрали за избор на нулевия потенциал, удовлетворява тази симетрия.



ориз. 283
Нека обозначим потенциала на положително заредена плоча +φ о, тогава потенциалът на отрицателно заредената плоча ще бъде равен на φ о. Тези потенциали могат лесно да бъдат определени, като се използва намерената стойност на силата на полето между плочите и връзката между силата и потенциалната разлика електрическо поле. Уравнението на тази връзка в този случай има формата +φo − φ o = Eh. От тази връзка определяме стойностите на потенциалите на плочата φ o = σh/(2ε o). Като се има предвид, че полето е равномерно между плочите (следователно потенциалът се променя линейно) и няма поле извън плочите (следователно потенциалът е постоянен тук), зависимостта на потенциала от координатата zизглежда (фиг. 284)

ориз. 284

 Задачи за самостоятелна работа.
 1. Във всички разгледани примери извършете обратната операция: като използвате намереното потенциално разпределение по формулата E x = −Δφ/Δxизчислете силните страни на разглежданите полета.
 2. Изведете формула (6) строго.
 3. Обяснете качествено следния „парадокс“. В полето на плосък кондензатор потенциалът "безкрайност" е двусмислено дефиниран: при движение в положителната посока на оста Зпотенциалът на „безкрайността“ се оказа равен −φo; при движение в отрицателна посока на ос З − +φ о, при движение по осите хили Y− е равно на нула. И така, какъв е потенциалът на „безкрайността“ в реална система от две плочи с крайни размери?

1 Такава система се нарича плосък кондензатор, ще проучим тези устройства по-подробно по-късно.

Да приемем, че зарядът е положителен. Равнината е заредена с постоянна повърхностна плътност. От симетрията следва, че интензитетът във всяка точка на полето има посока, перпендикулярна на равнината (фиг. 2.10). Очевидно е, че в точки, симетрични спрямо равнината, напрегнатостта на полето е еднаква по големина и противоположна по посока.

Нека изберем област от заредената равнина. Нека оградим тази област със затворена повърхност. Като затворена повърхнина нека си представим цилиндрична повърхнина с образуващи, перпендикулярни на равнината и основи на величина , разположени симетрично спрямо равнината. Нека приложим теоремата на Гаус към тази повърхност . Няма да има поток през страната на повърхността, тъй като във всяка точка той е нула. За бази същото като . Следователно общият поток през повърхността ще бъде равен на . Вътре в повърхността има заряд. Според теоремата на Гаус трябва да е изпълнено следното условие: , където . (3)

Полученият резултат не зависи от дължината на цилиндъра, т.е. на всяко разстояние от равнината напрегнатостта на полето е еднаква по величина. Картината на линиите на напрежение изглежда както е показано на фиг. 2.11. За отрицателно заредена равнина посоките на векторите ще се променят на противоположни. Ако равнината е с крайни размери, тогава полученият резултат ще бъде валиден само за точки, чието разстояние от ръба на плочата значително надвишава разстоянието от самата плоча (фиг. 2.12).