Električno polje jednoliko nabijene ravni. Primjena Gaussove teoreme za izračunavanje polja beskonačne ravnomjerno nabijene ravni

Ranije smo to pokazali električno polje, stvoren od beskonačne jednolično nabijene ploče je homogena, odnosno jačina polja je ista u svim tačkama, a vektor jačine je usmjeren okomito na ravan, a njegov modul je jednak E o = σ/(2ε o). Familija linija sila takvog polja je skup paralelnih linija okomitih na ploču. Na sl. 275, 276 također prikazuje dijagram projekcije vektora jačine polja Ez po osovini Z okomito na ploču (početak ove ose stavljamo na ploču). Jasno je da potencijal ovog polja zavisi samo od koordinata z, odnosno ekvipotencijalne površine u ovom slučaju su ravni paralelne naelektrisanoj ploči.



pirinač. 275



pirinač. 276
Uz tradicionalni izbor nivoa nultog potencijala φ(z → ∞), potencijal proizvoljne tačke jednak je radu pomicanja jediničnog pozitivnog naboja iz date tačke u beskonačnost. Budući da je modul napetosti konstantan, takav rad (i, prema tome, potencijal) ispada jednak beskonačnosti! Stoga je naznačeni izbor nivoa nultog potencijala u ovom slučaju neprikladan.
Stoga treba koristiti proizvoljnost izbora nultog nivoa. Dovoljno je odabrati proizvoljnu tačku sa koordinatama z = z o, i dodijelite mu proizvoljnu vrijednost potencijala φ(z o) = φ o(Sl. 277).

pirinač. 277
Sada, da izračunamo vrijednost potencijala u proizvoljnoj tački φ(z), možemo koristiti odnos između jačine i potencijala polja

S obzirom da je u ovom slučaju jačina polja konstantna (at z > 0) ovaj izraz se piše kao

iz čega slijedi željena zavisnost potencijala od koordinate (za z > 0)

Konkretno, može se postaviti proizvoljna vrijednost potencijala same ploče, odnosno staviti na z = z o = 0, φ = φ o. Tada je vrijednost potencijala u proizvoljnoj tački određena funkcijom

čiji je grafikon prikazan na slici 278.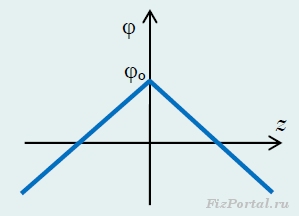

pirinač. 278
Činjenica da se potencijal u odnosu na beskonačnost pokazao beskonačno velik je sasvim očigledna - na kraju krajeva, beskonačna ploča također ima beskonačno veliki naboj. Kao što smo već naglasili, takav sistem je idealizacija – ne postoje beskonačne ploče. U stvarnosti, sva tijela imaju konačne dimenzije, pa je za njih moguć tradicionalni izbor nultog potencijala, iako u ovom slučaju raspodjela polja može biti vrlo komplikovana. U okviru razmatrane idealizacije, pogodnije je koristiti izbor nulte razine koju koristimo.

Nađimo raspodjelu potencijala polja koje stvaraju dvije identične, jednoliko nabijene paralelne ploče, čija su naelektrisanja jednaka po apsolutnoj vrijednosti i suprotna po predznaku 1 (Sl. 279).

Rice. 279
Označimo površinsku gustinu naboja na jednoj ploči +σ , i sa druge strane −σ . Udaljenost između ploča h smatraćemo da je mnogo manji od dimenzija ploča. Uvodimo koordinatni sistem, os z koja je okomita na ploče, polazište koordinata postavljamo u sredinu između ploča. Očigledno, za beskonačno velike ploče, sve karakteristike polja (jačina i potencijal) zavise samo od koordinata z. Za izračunavanje jačine polja u različitim tačkama u prostoru koristimo dobijeni izraz za jačinu polja koju stvara beskonačna ravnomerno naelektrisana ploča i princip superpozicije.
Svaka ravnomjerno nabijena ploča stvara jednolično polje čiji je modul intenziteta jednak E o = σ/(2ε o), a pravci su prikazani na slikama 280, 281.



pirinač. 280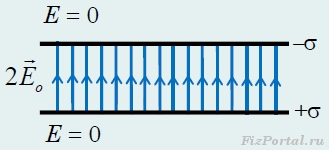

pirinač. 281
Zbrajanjem jačine polja po principu superpozicije dobijamo da je u prostoru između ploča jačina polja E = 2E o = σ/ε o dvostruku jačinu polja jedne ploče (ovdje su polja pojedinih ploča paralelna), a izvan ploča nema polja (ovdje su polja pojedinačnih ploča suprotna).
Strogo govoreći, za ploče konačnih dimenzija polje nije jednolično; linije polja polja ploča konačnih dimenzija prikazane su na slici 282.



pirinač. 282
Najjača odstupanja od uniformnosti uočavaju se u blizini rubova ploča (često se ova odstupanja nazivaju rubni efekti). Međutim, u oblasti koja se nalazi pored sredine ploča, polje se može smatrati uniformnim sa visokim stepenom tačnosti, odnosno ivični efekti se mogu zanemariti u ovoj oblasti. Imajte na umu da su greške u ovoj aproksimaciji manje, što je manji omjer udaljenosti između ploča i njihovih dimenzija.
Da bi se nedvosmisleno odredila raspodjela potencijala polja, potrebno je odabrati nivo nultog potencijala. Pretpostavićemo da je potencijal jednak nuli u ravni koja se nalazi u sredini između ploča, odnosno postavljamo φ = 0 at z = 0.
Uprkos proizvoljnosti u izboru nultog nivoa potencijala, naš izbor se može logički opravdati na osnovu simetrije sistema. Zaista, razmatrani sistem naelektrisanja se ogleda u refleksiji ogledala u odnosu na ravan z = 0 i istovremenu promjenu znakova naboja. Stoga je poželjno da i raspodjela potencijala ima istu simetriju: obnavlja se refleksijom u zrcalu uz istovremenu promjenu predznaka svih funkcija polja. Metoda koju smo odabrali za izbor nultog potencijala zadovoljava ovu simetriju.



pirinač. 283
Označite potencijal pozitivno nabijene ploče +φo, tada će potencijal negativno nabijene ploče biti jednak φo. Ove potencijale je lako odrediti koristeći pronađenu vrijednost jačine polja između ploča i odnos između jačine i potencijalne razlike električno polje. Jednačina ove veze u ovom slučaju ima oblik +φo − φo = Eh. Iz ove relacije određujemo vrijednosti potencijala ploča φ o = σh/(2ε o). Uzimajući u obzir da je polje ujednačeno između ploča (dakle, potencijal se linearno mijenja), a da nema polja izvan ploča (dakle, potencijal je ovdje konstantan), ovisnost potencijala o koordinatama z ima oblik (Sl. 284)

pirinač. 284

 Zadaci za samostalan rad.
 1. U svim razmatranim primjerima izvedite inverznu operaciju: prema pronađenoj raspodjeli potencijala koristeći formulu E x = −∆φ/∆x izračunajte jačine razmatranih polja.
 2. Strogo izvedite formulu (6).
 3. Kvalitativno objasnite sljedeći "paradoks". U polju ravnog kondenzatora, potencijal "beskonačnosti" je dvosmisleno definiran: kada se kreće u pozitivnom smjeru ose Z ispostavilo se da je potencijal "beskonačnosti" jednak −φ o; kada se kreće u negativnom smjeru ose Z − +φo, kada se kreće duž osi X ili Y− jednako nuli. Dakle, koji je potencijal "beskonačnosti" u stvarnom sistemu od dvije ploče konačnih veličina?

1 Takav sistem se zove ravni kondenzator, kasnije ćemo detaljnije proučiti ove uređaje.

Pretpostavićemo da je naelektrisanje pozitivno. Ravan je nabijena konstantnom površinskom gustinom. Iz simetrije sledi da intenzitet u bilo kojoj tački polja ima pravac okomit na ravan (slika 2.10). Očigledno, u tačkama koje su simetrične u odnosu na ravan, jačina polja je ista po veličini i suprotnog smera.

Izdvojimo područje na nabijenoj ravni. Okružite ovo područje zatvorenom površinom. Kao zatvorenu površinu zamišljamo cilindričnu površinu sa generatorima okomitim na ravan i bazama veličine koje se nalaze simetrično u odnosu na ravan. Primijenite na ovu površinu Gaussovu teoremu . Neće biti protoka kroz bočni dio površine, jer je jednak nuli u svakoj njenoj tački. Za baze, to je isto kao . Stoga će ukupni protok kroz površinu biti jednak . Unutar površine postoji naelektrisanje. Prema Gaussovoj teoremi, mora biti zadovoljen sljedeći uslov: , gdje . (3)

Dobiveni rezultat ne zavisi od dužine cilindra, tj. na bilo kojoj udaljenosti od ravni, jačina polja je ista po veličini. Obrazac zateznih linija izgleda kao što je prikazano na Sl. 2.11. Za negativno nabijenu ravan, smjerovi vektora će biti obrnuti. Ako je ravan konačnih dimenzija, onda će dobijeni rezultat vrijediti samo za tačke čija udaljenost od ruba ploče znatno premašuje udaljenost od same ploče (slika 2.12).