Inkompatible Systeme. Systeme mit allgemeiner Lösung. Private Lösungen. Drei Fälle beim Lösen linearer Gleichungssysteme
Ein System linearer Gleichungen ist eine Vereinigung von n linearen Gleichungen, von denen jede k Variablen enthält. Es ist so geschrieben:
Viele glauben, wenn sie zum ersten Mal mit höherer Algebra in Berührung kommen, fälschlicherweise, dass die Anzahl der Gleichungen notwendigerweise mit der Anzahl der Variablen übereinstimmen muss. In der Schulalgebra geschieht dies normalerweise, in der höheren Algebra trifft dies jedoch im Allgemeinen nicht zu.
Die Lösung eines Gleichungssystems ist eine Zahlenfolge (k 1, k 2, ..., k n), die die Lösung für jede Gleichung des Systems ist, d.h. Wenn man in diese Gleichung anstelle der Variablen x 1, x 2, ... einsetzt, ergibt x n die korrekte numerische Gleichheit.
Das Lösen eines Gleichungssystems bedeutet dementsprechend, die Menge aller seiner Lösungen zu finden oder zu beweisen, dass diese Menge leer ist. Da die Anzahl der Gleichungen und die Anzahl der Unbekannten möglicherweise nicht übereinstimmen, sind drei Fälle möglich:
- Das System ist inkonsistent, d.h. die Menge aller Lösungen ist leer. Ein eher seltener Fall, der leicht erkannt werden kann, unabhängig davon, welche Methode zur Lösung des Systems verwendet wird.
- Das System ist konsistent und bestimmt, d.h. hat genau eine Lösung. Die klassische Version, seit der Schule bekannt.
- Das System ist konsistent und undefiniert, d.h. hat unendlich viele Lösungen. Dies ist die schwierigste Option. Es reicht nicht aus, darauf hinzuweisen, dass „das System eine unendliche Menge von Lösungen hat“ – es ist notwendig, zu beschreiben, wie diese Menge strukturiert ist.
Eine Variable x i heißt erlaubt, wenn sie nur in einer Gleichung des Systems enthalten ist und einen Koeffizienten von 1 hat. Mit anderen Worten, in anderen Gleichungen muss der Koeffizient der Variablen x i gleich Null sein.
Wenn wir in jeder Gleichung eine zulässige Variable auswählen, erhalten wir einen Satz zulässiger Variablen für das gesamte Gleichungssystem. Das in dieser Form geschriebene System selbst wird auch als aufgelöst bezeichnet. Generell lässt sich sagen, dass ein und dasselbe ursprüngliche System auf verschiedene zulässige Systeme reduziert werden kann, aber das beschäftigt uns vorerst nicht. Hier sind Beispiele für zulässige Systeme:

Beide Systeme werden hinsichtlich der Variablen x 1 , x 3 und x 4 aufgelöst. Mit dem gleichen Erfolg kann jedoch argumentiert werden, dass das zweite System in Bezug auf x 1, x 3 und x 5 aufgelöst wird. Es reicht aus, die allerletzte Gleichung in der Form x 5 = x 4 umzuschreiben.
Betrachten wir nun einen allgemeineren Fall. Wir haben insgesamt k Variablen, von denen r erlaubt sind. Dann sind zwei Fälle möglich:
- Die Anzahl der erlaubten Variablen r ist gleich der Gesamtzahl der Variablen k: r = k. Wir erhalten ein System von k Gleichungen, in denen r = k erlaubte Variablen sind. Ein solches System ist einheitlich und eindeutig, weil x 1 = b 1, x 2 = b 2, ..., x k = b k;
- Die Anzahl der zulässigen Variablen r ist kleiner als die Gesamtzahl der Variablen k: r< k . Остальные (k − r ) переменных называются свободными - они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.
In den obigen Systemen sind also die Variablen x 2, x 5, x 6 (für das erste System) und x 2, x 5 (für das zweite) frei. Der Fall, dass es freie Variablen gibt, lässt sich besser als Satz formulieren:
Bitte beachten Sie: Dies ist ein sehr wichtiger Punkt! Je nachdem, wie Sie das resultierende System schreiben, kann dieselbe Variable entweder erlaubt oder frei sein. Die meisten Dozenten für höhere Mathematik empfehlen, Variablen in lexikografischer Reihenfolge aufzuschreiben, d. h. aufsteigender Index. Sie sind jedoch nicht verpflichtet, diesem Rat zu folgen.
Satz. Wenn in einem System von n Gleichungen die Variablen x 1, x 2, ..., x r erlaubt sind und x r + 1, x r + 2, ..., x k frei sind, dann:
- Wenn wir die Werte der freien Variablen festlegen (x r + 1 = t r + 1, x r + 2 = t r + 2, ..., x k = t k) und dann die Werte x 1, x 2 finden, ..., x r, wir erhalten eine der Entscheidungen.
- Wenn in zwei Lösungen die Werte freier Variablen übereinstimmen, dann stimmen auch die Werte zulässiger Variablen überein, d.h. Lösungen sind gleich.
Was bedeutet dieser Satz? Um alle Lösungen eines aufgelösten Gleichungssystems zu erhalten, genügt es, die freien Variablen zu isolieren. Wenn wir dann den freien Variablen unterschiedliche Werte zuweisen, erhalten wir vorgefertigte Lösungen. Das ist alles – auf diese Weise erhalten Sie alle Lösungen des Systems. Es gibt keine anderen Lösungen.
Fazit: Das aufgelöste Gleichungssystem ist immer konsistent. Wenn die Anzahl der Gleichungen in einem aufgelösten System gleich der Anzahl der Variablen ist, ist das System definitiv; wenn weniger, ist es unbestimmt.
Und alles wäre gut, aber es stellt sich die Frage: Wie erhält man aus dem ursprünglichen Gleichungssystem ein aufgelöstes? Dafür gibt es
Ein System linearer Agebraischer Gleichungen (SLAEs) auf Konsistenz zu untersuchen bedeutet, herauszufinden, ob dieses System Lösungen hat oder nicht. Nun, wenn es Lösungen gibt, dann geben Sie an, wie viele es gibt.
Wir benötigen Informationen aus dem Thema „System linearer algebraischer Gleichungen. Grundbegriffe. Matrixform der Notation“. Insbesondere werden Konzepte wie Systemmatrix und erweiterte Systemmatrix benötigt, da die Formulierung des Kronecker-Capelli-Theorems auf ihnen basiert. Wie üblich bezeichnen wir die Systemmatrix mit dem Buchstaben $A$ und die erweiterte Matrix des Systems mit dem Buchstaben $\widetilde(A)$.
Kronecker-Capelli-Theorem
Ein System linearer algebraischer Gleichungen ist genau dann konsistent, wenn der Rang der Systemmatrix gleich dem Rang der erweiterten Matrix des Systems ist, d. h. $\rang A=\rang\widetilde(A)$.
Ich möchte Sie daran erinnern, dass ein System als Gelenk bezeichnet wird, wenn es mindestens eine Lösung hat. Das Kronecker-Capelli-Theorem besagt Folgendes: Wenn $\rang A=\rang\widetilde(A)$, dann gibt es eine Lösung; Wenn $\rang A\neq\rang\widetilde(A)$, dann hat dieses SLAE keine Lösungen (inkonsistent). Die Antwort auf die Frage nach der Anzahl dieser Lösungen gibt eine Folgerung des Kronecker-Capelli-Theorems. Bei der Formulierung des Korollars wird der Buchstabe $n$ verwendet, der der Anzahl der Variablen des gegebenen SLAE entspricht.
Folgerung zum Kronecker-Capelli-Theorem
- Wenn $\rang A\neq\rang\widetilde(A)$, dann ist das SLAE inkonsistent (hat keine Lösungen).
- Wenn $\rang A=\rang\widetilde(A)< n$, то СЛАУ является неопределённой (имеет бесконечное количество решений).
- Wenn $\rang A=\rang\widetilde(A) = n$, dann ist der SLAE definit (hat genau eine Lösung).
Bitte beachten Sie, dass der formulierte Satz und seine Folgerung keinen Hinweis darauf geben, wie eine Lösung für das SLAE gefunden werden kann. Mit ihrer Hilfe kann man nur herausfinden, ob es diese Lösungen gibt oder nicht und wenn ja, wie viele.
Beispiel Nr. 1
Erkunden Sie SLAE $ \left \(\begin(aligned) & -3x_1+9x_2-7x_3=17;\\ & -x_1+2x_2-4x_3=9;\\ & 4x_1-2x_2+19x_3=-42. \end(aligned )\right.$ für Kompatibilität. Wenn das SLAE kompatibel ist, geben Sie die Anzahl der Lösungen an.
Um die Existenz von Lösungen für ein gegebenes SLAE herauszufinden, verwenden wir das Kronecker-Capelli-Theorem. Wir benötigen die Matrix des Systems $A$ und die erweiterte Matrix des Systems $\widetilde(A)$, wir werden sie schreiben:
$$ A=\left(\begin(array) (ccc) -3 & 9 & -7 \\ -1 & 2 & -4 \\ 4 & -2 & 19 \end(array) \right);\; \widetilde(A)=\left(\begin(array) (ccc|c) -3 & 9 &-7 & 17 \\ -1 & 2 & -4 & 9\\ 4 & -2 & 19 & -42 \end(array) \right). $$
Wir müssen $\rang A$ und $\rang\widetilde(A)$ finden. Es gibt viele Möglichkeiten, dies zu tun, von denen einige im Abschnitt „Matrix-Rang“ aufgeführt sind. Typischerweise werden zur Untersuchung solcher Systeme zwei Methoden verwendet: „Berechnung des Rangs einer Matrix per Definition“ oder „Berechnung des Rangs einer Matrix mit der Methode der Elementartransformationen“.
Methode Nummer 1. Berechnung von Rängen per Definition.
Laut Definition ist Rang die höchste Ordnung der Minderjährigen einer Matrix, unter denen es mindestens eines gibt, das von Null verschieden ist. Normalerweise beginnt das Studium mit Minor-Werten erster Ordnung, aber hier ist es bequemer, sofort mit der Berechnung des Minor-Werts dritter Ordnung der Matrix $A$ zu beginnen. Die Nebenelemente dritter Ordnung liegen am Schnittpunkt von drei Zeilen und drei Spalten der betreffenden Matrix. Da die Matrix $A$ nur 3 Zeilen und 3 Spalten enthält, ist der Minor dritter Ordnung der Matrix $A$ die Determinante der Matrix $A$, d.h. $\Delta A$. Zur Berechnung der Determinante wenden wir Formel Nr. 2 aus dem Thema „Formeln zur Berechnung von Determinanten zweiter und dritter Ordnung“ an:
$$ \Delta A=\left| \begin(array) (ccc) -3 & 9 & -7 \\ -1 & 2 & -4 \\ 4 & -2 & 19 \end(array) \right|=-21. $$
Es gibt also einen Minor dritter Ordnung der Matrix $A$, der ungleich Null ist. Es ist unmöglich, ein Minor vierter Ordnung zu konstruieren, da es 4 Zeilen und 4 Spalten erfordert und die Matrix $A$ nur 3 Zeilen und 3 Spalten hat. Die höchste Ordnung der Minderjährigen der Matrix $A$, unter denen es mindestens eine gibt, die ungleich Null ist, ist also gleich 3. Daher ist $\rang A=3$.
Wir müssen auch $\rang\widetilde(A)$ finden. Schauen wir uns die Struktur der Matrix $\widetilde(A)$ an. Bis zur Zeile in der Matrix $\widetilde(A)$ gibt es Elemente der Matrix $A$, und wir haben herausgefunden, dass $\Delta A\neq 0$. Folglich hat die Matrix $\widetilde(A)$ einen Nebenwert dritter Ordnung, der ungleich Null ist. Wir können keine Minderjährigen vierter Ordnung der Matrix $\widetilde(A)$ konstruieren, daher schließen wir: $\rang\widetilde(A)=3$.
Da $\rang A=\rang\widetilde(A)$ ist, ist das System nach dem Kronecker-Capelli-Theorem konsistent, d. h. hat eine Lösung (mindestens eine). Um die Anzahl der Lösungen anzugeben, berücksichtigen wir, dass unser SLAE drei Unbekannte enthält: $x_1$, $x_2$ und $x_3$. Da die Anzahl der Unbekannten $n=3$ beträgt, schließen wir: $\rang A=\rang\widetilde(A)=n$, daher ist das System gemäß der Folgerung des Kronecker-Capelli-Theorems definit, d. h. hat eine einzigartige Lösung.
Das Problem ist behoben. Welche Nachteile und Vorteile hat diese Methode? Lassen Sie uns zunächst über die Vorteile sprechen. Erstens mussten wir nur eine Determinante finden. Danach haben wir sofort eine Schlussfolgerung über die Anzahl der Lösungen gezogen. Typischerweise ergeben Standardberechnungen Gleichungssysteme, die drei Unbekannte enthalten und eine eindeutige Lösung haben. Für solche Systeme ist diese Methode sehr praktisch, da wir im Voraus wissen, dass es eine Lösung gibt (sonst wäre das Beispiel nicht in der Standardberechnung enthalten). Diese. Alles, was wir tun müssen, ist, die Existenz einer Lösung auf dem schnellsten Weg nachzuweisen. Zweitens wird der berechnete Wert der Determinante der Systemmatrix (d. h. $\Delta A$) später nützlich sein: wenn wir beginnen, ein gegebenes System mit der Cramer-Methode oder mit der inversen Matrix zu lösen.
Die Methode zur Rangberechnung ist jedoch per Definition unerwünscht, wenn die Matrix des Systems $A$ rechteckig ist. In diesem Fall ist es besser, die zweite Methode zu verwenden, die weiter unten besprochen wird. Wenn außerdem $\Delta A=0$ ist, können wir nichts über die Anzahl der Lösungen eines gegebenen inhomogenen SLAE sagen. Vielleicht hat die SLAE unendlich viele Lösungen, vielleicht aber auch keine. Wenn $\Delta A=0$, dann sind zusätzliche Recherchen erforderlich, die oft umständlich sind.
Um das Gesagte zusammenzufassen, stelle ich fest, dass die erste Methode für diejenigen SLAEs geeignet ist, deren Systemmatrix quadratisch ist. Darüber hinaus enthält der SLAE selbst drei oder vier Unbekannte und wird aus Standardberechnungen oder -tests entnommen.
Methode Nummer 2. Rangberechnung nach der Methode der Elementartransformationen.
Diese Methode wird im entsprechenden Thema ausführlich beschrieben. Wir beginnen mit der Berechnung des Rangs der Matrix $\widetilde(A)$. Warum Matrizen $\widetilde(A)$ und nicht $A$? Tatsache ist, dass die Matrix $A$ Teil der Matrix $\widetilde(A)$ ist, daher werden wir durch die Berechnung des Rangs der Matrix $\widetilde(A)$ gleichzeitig den Rang der Matrix $A$ ermitteln .
\begin(aligned) &\widetilde(A) =\left(\begin(array) (ccc|c) -3 & 9 &-7 & 17 \\ -1 & 2 & -4 & 9\\ 4 & - 2 & 19 & -42 \end(array) \right) \rightarrow \left|\text(erste und zweite Zeile vertauschen)\right| \rightarrow \\ &\rightarrow \left(\begin(array) (ccc|c) -1 & 2 & -4 & 9 \\ -3 & 9 &-7 & 17\\ 4 & -2 & 19 & - 42 \end(array) \right) \begin(array) (l) \phantom(0) \\ II-3\cdot I\\ III+4\cdot I \end(array) \rightarrow \left(\begin (array) (ccc|c) -1 & 2 & -4 & 9 \\ 0 & 3 &5 & -10\\ 0 & 6 & 3 & -6 \end(array) \right) \begin(array) ( l) \phantom(0) \\ \phantom(0)\\ III-2\cdot II \end(array)\rightarrow\\ &\rightarrow \left(\begin(array) (ccc|c) -1 & 2 & -4 & 9 \\ 0 & 3 &5 & -10\\ 0 & 0 & -7 & 14 \end(array) \right) \end(aligned)
Wir haben die Matrix $\widetilde(A)$ auf die Trapezform reduziert. Auf der Hauptdiagonale der resultierenden Matrix $\left(\begin(array) (ccc|c) -1 & 2 & -4 & 9 \\ 0 & 3 &5 & -10\\ 0 & 0 & -7 & 14 \end( array) \right)$ enthält drei Nicht-Null-Elemente: -1, 3 und -7. Fazit: Der Rang der Matrix $\widetilde(A)$ ist 3, d.h. $\rang\widetilde(A)=3$. Wenn wir Transformationen mit den Elementen der Matrix $\widetilde(A)$ durchführen, transformieren wir gleichzeitig die Elemente der Matrix $A$, die sich bis zur Linie befinden. Die Matrix $A$ wird ebenfalls auf die Trapezform reduziert: $\left(\begin(array) (ccc) -1 & 2 & -4 \\ 0 & 3 &5 \\ 0 & 0 & -7 \end(array) \richtig )$. Fazit: Der Rang der Matrix $A$ ist ebenfalls 3, d.h. $\rang A=3$.
Da $\rang A=\rang\widetilde(A)$ ist, ist das System nach dem Kronecker-Capelli-Theorem konsistent, d. h. hat eine Lösung. Um die Anzahl der Lösungen anzugeben, berücksichtigen wir, dass unser SLAE drei Unbekannte enthält: $x_1$, $x_2$ und $x_3$. Da die Anzahl der Unbekannten $n=3$ beträgt, schließen wir: $\rang A=\rang\widetilde(A)=n$, daher ist das System gemäß der Folgerung des Kronecker-Capelli-Theorems definiert, d.h. hat eine einzigartige Lösung.
Welche Vorteile bietet die zweite Methode? Der Hauptvorteil ist seine Vielseitigkeit. Es spielt für uns keine Rolle, ob die Matrix des Systems quadratisch ist oder nicht. Darüber hinaus haben wir tatsächlich Vorwärtstransformationen der Gaußschen Methode durchgeführt. Es bleiben nur noch ein paar Schritte und wir könnten eine Lösung für dieses SLAE finden. Ehrlich gesagt gefällt mir die zweite Methode besser als die erste, aber die Wahl ist Geschmackssache.
Antwort: Der angegebene SLAE ist konsistent und definiert.
Beispiel Nr. 2
SLAE erkunden $ \left\( \begin(aligned) & x_1-x_2+2x_3=-1;\\ & -x_1+2x_2-3x_3=3;\\ & 2x_1-x_2+3x_3=2;\\ & 3x_1- 2x_2+5x_3=1;\\ & 2x_1-3x_2+5x_3=-4.\end(aligned) \right.$ aus Kompatibilitätsgründen.
Die Ränge der Systemmatrix und der erweiterten Systemmatrix ermitteln wir mit der Methode der Elementartransformationen. Erweiterte Systemmatrix: $\widetilde(A)=\left(\begin(array) (ccc|c) 1 & -1 & 2 & -1\\ -1 & 2 & -3 & 3 \\ 2 & -1 & 3 & 2 \\ 3 & -2 & 5 & 1 \\ 2 & -3 & 5 & -4 \end(array) \right)$. Finden wir die erforderlichen Ränge, indem wir die erweiterte Matrix des Systems transformieren:

Die erweiterte Matrix des Systems wird auf eine Stufenform reduziert. Wenn eine Matrix auf die Staffelform reduziert wird, ist ihr Rang gleich der Anzahl der Zeilen ungleich Null. Daher ist $\rang A=3$. Die Matrix $A$ (bis zur Geraden) wird auf Trapezform reduziert und ihr Rang ist 2, $\rang A=2$.

Da $\rang A\neq\rang\widetilde(A)$ ist, ist das System gemäß dem Kronecker-Capelli-Theorem inkonsistent (d. h. es hat keine Lösungen).
Antwort: Das System ist inkonsistent.
Beispiel Nr. 3
Erkunden Sie SLAE $ \left\( \begin(aligned) & 2x_1+7x_3-5x_4+11x_5=42;\\ & x_1-2x_2+3x_3+2x_5=17;\\ & -3x_1+9x_2-11x_3-7x_5=-64 ;\\ & -5x_1+17x_2-16x_3-5x_4-4x_5=-90;\\ & 7x_1-17x_2+23x_3+15x_5=132. \end(aligned) \right.$ aus Kompatibilitätsgründen.
Die erweiterte Matrix des Systems hat die Form: $\widetilde(A)=\left(\begin(array) (ccccc|c) 2 & 0 & 7 & -5 & 11 & 42\\ 1 & -2 & 3 & 0 & 2 & 17 \\ -3 & 9 & -11 & 0 & -7 & -64 \\ -5 & 17 & -16 & -5 & -4 & -90 \\ 7 & -17 & 23 & 0 & 15 & 132 \end(array) \right)$. Vertauschen wir die erste und zweite Zeile dieser Matrix, sodass das erste Element der ersten Zeile eins wird: $\left(\begin(array) (ccccc|c) 1 & -2 & 3 & 0 & 2 & 17\\ 2 & 0 & 7 & -5 & 11 & 42 \\ -3 & 9 & -11 & 0 & -7 & -64 \\ -5 & 17 & -16 & -5 & -4 & -90 \\ 7 & -17 & 23 & 0 & 15 & 132 \end(array) \right)$.

Wir haben die erweiterte Matrix des Systems und die Matrix des Systems selbst auf eine Trapezform reduziert. Der Rang der erweiterten Matrix des Systems ist gleich drei, der Rang der Matrix des Systems ist ebenfalls gleich drei. Da das System $n=5$ Unbekannte enthält, d.h. $\rang\widetilde(A)=\rang A< n$, то согласно следствия из теоремы Кронекера-Капелли данная система является неопределённой, т.е. имеет бесконечное количество решений.
Antwort: Das System ist unsicher.
Im zweiten Teil analysieren wir Beispiele, die häufig in Standardberechnungen oder Tests in der höheren Mathematik enthalten sind: Konsistenzforschung und Lösung von SLAE in Abhängigkeit von den Werten der darin enthaltenen Parameter.
In der Praxis sind jedoch zwei weitere Fälle weit verbreitet:
– Das System ist inkonsistent (hat keine Lösungen);
– Das System ist konsistent und hat unendlich viele Lösungen.
Notiz : Der Begriff „Konsistenz“ impliziert, dass das System zumindest eine Lösung hat. Bei einer Reihe von Problemen ist es notwendig, das System zunächst auf Kompatibilität zu prüfen. Wie das geht, erfahren Sie im Artikel über Rang der Matrizen.
Für diese Systeme wird die universellste aller Lösungsmethoden verwendet – Gaußsche Methode. Tatsächlich führt auch die „Schul“-Methode zur Antwort, aber in der höheren Mathematik ist es üblich, die Gaußsche Methode der sequentiellen Eliminierung von Unbekannten zu verwenden. Diejenigen, die mit dem Gaußschen Methodenalgorithmus nicht vertraut sind, lesen bitte zuerst die Lektion Gaußsche Methode für Dummies.
Die elementaren Matrixtransformationen selbst sind genau gleich, der Unterschied liegt im Ende der Lösung. Schauen wir uns zunächst einige Beispiele an, bei denen das System keine Lösungen hat (inkonsistent).
Beispiel 1
Was fällt Ihnen an diesem System sofort ins Auge? Die Anzahl der Gleichungen ist geringer als die Anzahl der Variablen. Wenn die Anzahl der Gleichungen kleiner ist als die Anzahl der Variablen, dann können wir sofort sagen, dass das System entweder inkonsistent ist oder unendlich viele Lösungen hat. Und es bleibt nur noch, es herauszufinden.
Der Anfang der Lösung ist völlig gewöhnlich – wir schreiben die erweiterte Matrix des Systems auf und bringen sie mithilfe elementarer Transformationen in eine schrittweise Form:

(1) Im oberen linken Schritt müssen wir +1 oder –1 erhalten. In der ersten Spalte gibt es solche Zahlen nicht, daher bringt eine Neuanordnung der Zeilen nichts. Die Einheit muss sich selbst organisieren, und dies kann auf verschiedene Weise erfolgen. Ich habe Folgendes gemacht: Zur ersten Zeile fügen wir die dritte Zeile hinzu, multipliziert mit –1.
(2) Nun erhalten wir in der ersten Spalte zwei Nullen. Zur zweiten Zeile addieren wir die erste Zeile multipliziert mit 3. Zur dritten Zeile addieren wir die erste Zeile multipliziert mit 5.
(3) Nach Abschluss der Transformation ist es immer ratsam zu prüfen, ob es möglich ist, die resultierenden Zeichenfolgen zu vereinfachen. Dürfen. Wir dividieren die zweite Zeile durch 2 und erhalten gleichzeitig im zweiten Schritt die erforderliche –1. Teilen Sie die dritte Zeile durch –3.
(4) Fügen Sie die zweite Zeile zur dritten Zeile hinzu.
Wahrscheinlich ist jedem die schlechte Linie aufgefallen, die aus elementaren Transformationen resultierte: ![]() . Es ist klar, dass das nicht so sein kann. Schreiben wir tatsächlich die resultierende Matrix neu
. Es ist klar, dass das nicht so sein kann. Schreiben wir tatsächlich die resultierende Matrix neu  zurück zum linearen Gleichungssystem:
zurück zum linearen Gleichungssystem: 
Wenn als Ergebnis elementarer Transformationen eine Zeichenfolge der Form erhalten wird, wobei eine Zahl ungleich Null ist, dann ist das System inkonsistent (hat keine Lösungen).
Wie schreibe ich das Ende einer Aufgabe auf? Zeichnen wir mit weißer Kreide: „Als Ergebnis elementarer Transformationen erhält man eine Zeichenfolge der Form , wobei „“ und geben die Antwort: Das System hat keine Lösungen (inkonsistent).
Wenn es gemäß der Bedingung erforderlich ist, das System auf Kompatibilität zu untersuchen, ist es notwendig, die Lösung mithilfe des Konzepts in einem solideren Stil zu formalisieren Matrixrang und das Kronecker-Capelli-Theorem.
Bitte beachten Sie, dass es hier keine Umkehrung des Gaußschen Algorithmus gibt – es gibt keine Lösungen und es gibt einfach nichts zu finden.
Beispiel 2
Lösen Sie ein System linearer Gleichungen 
Dies ist ein Beispiel, das Sie selbst lösen können. Vollständige Lösung und Antwort am Ende der Lektion. Ich erinnere Sie noch einmal daran, dass Ihre Lösung von meiner Lösung abweichen kann; der Gaußsche Algorithmus weist keine starke „Starrheit“ auf.
Ein weiteres technisches Merkmal der Lösung: Elementartransformationen können gestoppt werden sofort, sobald eine Zeile wie , where . Betrachten wir ein bedingtes Beispiel: Nehmen wir an, dass nach der ersten Transformation die Matrix erhalten wird  . Die Matrix wurde noch nicht auf die Staffelform reduziert, aber es besteht keine Notwendigkeit für weitere elementare Transformationen, da eine Linie der Form aufgetaucht ist, wo . Es sollte sofort die Antwort gegeben werden, dass das System nicht kompatibel ist.
. Die Matrix wurde noch nicht auf die Staffelform reduziert, aber es besteht keine Notwendigkeit für weitere elementare Transformationen, da eine Linie der Form aufgetaucht ist, wo . Es sollte sofort die Antwort gegeben werden, dass das System nicht kompatibel ist.
Wenn ein lineares Gleichungssystem keine Lösungen hat, ist das fast ein Geschenk, da man eine kurze Lösung erhält, manchmal buchstäblich in 2-3 Schritten.
Aber alles auf dieser Welt ist ausgeglichen, und ein Problem, für das das System unendlich viele Lösungen hat, ist nur länger.
Beispiel 3
Lösen Sie ein System linearer Gleichungen 
Es gibt 4 Gleichungen und 4 Unbekannte, sodass das System entweder eine einzige Lösung oder keine Lösungen oder unendlich viele Lösungen haben kann. Wie dem auch sei, die Gaußsche Methode wird uns auf jeden Fall zur Antwort führen. Das ist seine Vielseitigkeit.
Der Anfang ist wieder Standard. Schreiben wir die erweiterte Matrix des Systems auf und bringen sie mithilfe elementarer Transformationen in eine schrittweise Form: 
Das ist alles, und du hattest Angst.
(1) Bitte beachten Sie, dass alle Zahlen in der ersten Spalte durch 2 teilbar sind, sodass 2 im oberen linken Schritt in Ordnung ist. Zur zweiten Zeile addieren wir die erste Zeile, multipliziert mit –4. Zur dritten Zeile addieren wir die erste Zeile, multipliziert mit –2. Zur vierten Zeile fügen wir die erste Zeile hinzu, multipliziert mit –1.
Aufmerksamkeit! Viele könnten von der vierten Zeile in Versuchung geführt werden subtrahieren erste Linie. Dies ist möglich, aber nicht notwendig; die Erfahrung zeigt, dass die Wahrscheinlichkeit eines Rechenfehlers um ein Vielfaches steigt. Fügen Sie einfach hinzu: Zur vierten Zeile addieren Sie die erste Zeile multipliziert mit –1 – genau so!
(2) Die letzten drei Zeilen sind proportional, zwei davon können gestrichen werden.
Auch hier müssen wir zeigen erhöhte Aufmerksamkeit, aber sind die Linien wirklich proportional? Um auf der sicheren Seite zu sein (besonders bei einer Teekanne), empfiehlt es sich, die zweite Zeile mit –1 zu multiplizieren und die vierte Zeile durch 2 zu dividieren, sodass drei identische Zeilen entstehen. Und erst danach zwei davon entfernen.
Durch elementare Transformationen wird die erweiterte Matrix des Systems auf eine schrittweise Form reduziert: 
Wenn Sie eine Aufgabe in ein Notizbuch schreiben, ist es aus Gründen der Übersichtlichkeit ratsam, dieselben Notizen mit Bleistift zu machen.
Schreiben wir das entsprechende Gleichungssystem um: 
Von einer „gewöhnlichen“ Einzellösung des Systems riecht es hier nicht. Es gibt auch keine schlechte Linie. Dies bedeutet, dass dies der dritte verbleibende Fall ist – das System hat unendlich viele Lösungen. Manchmal ist es je nach Bedingung notwendig, die Kompatibilität des Systems zu untersuchen (also nachzuweisen, dass es überhaupt eine Lösung gibt), darüber können Sie im letzten Absatz des Artikels nachlesen Wie finde ich den Rang einer Matrix? Aber lassen Sie uns zunächst die Grundlagen durchgehen:
Eine unendliche Menge von Lösungen für ein System wird kurz in der sogenannten Form geschrieben allgemeine Lösung des Systems .
Wir finden die allgemeine Lösung des Systems mithilfe der Umkehrung der Gaußschen Methode.
Zuerst müssen wir definieren, welche Variablen wir haben Basic, und welche Variablen frei. Sie müssen sich nicht mit den Begriffen der linearen Algebra herumschlagen, denken Sie nur daran, dass es solche gibt Grundvariablen Und freie Variablen.
Basisvariablen „sitzen“ immer strikt auf den Schritten der Matrix.
In diesem Beispiel sind die Grundvariablen und
Freie Variablen sind alles übrig Variablen, die keinen Schritt erhalten haben. In unserem Fall gibt es zwei davon: – freie Variablen.
Jetzt brauchen Sie Alle Grundvariablenäußern nur durch freie Variablen.
Die Umkehrung des Gaußschen Algorithmus funktioniert traditionell von unten nach oben.
Aus der zweiten Gleichung des Systems drücken wir die Grundvariable aus:
Schauen Sie sich nun die erste Gleichung an: ![]() . Zuerst ersetzen wir den gefundenen Ausdruck darin:
. Zuerst ersetzen wir den gefundenen Ausdruck darin: ![]()
Es bleibt noch, die Basisvariable durch freie Variablen auszudrücken: 
Am Ende haben wir bekommen, was wir brauchten - Alle Grundvariablen ( und ) werden ausgedrückt nur durch freie Variablen: ![]()
Eigentlich ist die allgemeine Lösung fertig: ![]()
Wie schreibe ich die allgemeine Lösung richtig?
Freie Variablen werden „von selbst“ und ausschließlich an ihrer Stelle in die allgemeine Lösung geschrieben. In diesem Fall sollten freie Variablen an der zweiten und vierten Position geschrieben werden:  .
.
Die resultierenden Ausdrücke für die Basisvariablen ![]() und muss natürlich an erster und dritter Stelle geschrieben werden:
und muss natürlich an erster und dritter Stelle geschrieben werden: 
Freie Variablen bereitstellen beliebige Werte, man kann unendlich viele finden private Lösungen. Die beliebtesten Werte sind Nullen, da die jeweilige Lösung am einfachsten zu erhalten ist. Setzen wir in die allgemeine Lösung ein: ![]()
– private Lösung.
Ein weiteres süßes Paar sind Einsen, ersetzen wir sie in der allgemeinen Lösung: ![]()
– eine weitere private Lösung.
Es ist leicht zu erkennen, dass das Gleichungssystem Folgendes hat unendlich viele Lösungen(da wir freie Variablen angeben können beliebig Werte)
Jede die jeweilige Lösung muss genügen zu jedem Gleichung des Systems. Dies ist die Grundlage für eine „schnelle“ Überprüfung der Richtigkeit der Lösung. Nehmen Sie zum Beispiel eine bestimmte Lösung und setzen Sie sie auf der linken Seite jeder Gleichung des ursprünglichen Systems ein: 
Alles muss zusammenpassen. Und bei jeder einzelnen Lösung, die Sie erhalten, sollte auch alles übereinstimmen.
Aber streng genommen täuscht die Prüfung einer bestimmten Lösung manchmal, d. h. Eine bestimmte Lösung kann jede Gleichung des Systems erfüllen, aber die allgemeine Lösung selbst wird tatsächlich falsch gefunden.
Daher ist die Überprüfung der allgemeinen Lösung gründlicher und zuverlässiger. So überprüfen Sie die resultierende allgemeine Lösung ![]() ?
?
Es ist nicht schwer, aber ziemlich mühsam. Wir müssen Ausdrücke akzeptieren Basic Variablen, in diesem Fall ![]() und und setze sie in die linke Seite jeder Gleichung des Systems ein.
und und setze sie in die linke Seite jeder Gleichung des Systems ein.
Auf der linken Seite der ersten Gleichung des Systems: 
Auf der linken Seite der zweiten Gleichung des Systems: 
Man erhält die rechte Seite der ursprünglichen Gleichung.
Beispiel 4
Lösen Sie das System mit der Gaußschen Methode. Finden Sie die allgemeine Lösung und zwei spezielle Lösungen. Überprüfen Sie die allgemeine Lösung. 
Dies ist ein Beispiel, das Sie selbst lösen können. Auch hier ist übrigens die Anzahl der Gleichungen geringer als die Anzahl der Unbekannten, was bedeutet, dass sofort klar ist, dass das System entweder inkonsistent sein wird oder unendlich viele Lösungen haben wird. Was ist im Entscheidungsprozess selbst wichtig? Achtung, und noch einmal Aufmerksamkeit. Vollständige Lösung und Antwort am Ende der Lektion.
Und noch ein paar Beispiele, um das Material zu verstärken
Beispiel 5
Lösen Sie ein System linearer Gleichungen. Wenn das System unendlich viele Lösungen hat, finden Sie zwei bestimmte Lösungen und überprüfen Sie die allgemeine Lösung 
Lösung: Schreiben wir die erweiterte Matrix des Systems auf und bringen sie mithilfe elementarer Transformationen in eine schrittweise Form: 
(1) Fügen Sie die erste Zeile zur zweiten Zeile hinzu. Zur dritten Zeile addieren wir die erste Zeile multipliziert mit 2. Zur vierten Zeile addieren wir die erste Zeile multipliziert mit 3.
(2) Zur dritten Zeile fügen wir die zweite Zeile hinzu, multipliziert mit –5. Zur vierten Zeile fügen wir die zweite Zeile hinzu, multipliziert mit –7.
(3) Die dritte und vierte Zeile sind gleich, wir löschen eine davon.
Das ist so eine Schönheit: 
Auf den Stufen sitzen Basisvariablen, also Basisvariablen.
Es gibt nur eine freie Variable, die keinen Schritt erhalten hat:
Umkehren:
Lassen Sie uns die Grundvariablen durch eine freie Variable ausdrücken:
Aus der dritten Gleichung: ![]()
Betrachten wir die zweite Gleichung und ersetzen wir den gefundenen Ausdruck darin: ![]()
![]()
Betrachten wir die erste Gleichung und ersetzen wir die gefundenen Ausdrücke darin: 
Ja, ein Taschenrechner, der gewöhnliche Brüche berechnet, ist immer noch praktisch.
Die allgemeine Lösung lautet also: ![]()
Noch einmal: Wie ist es ausgegangen? Die freie Variable steht allein an ihrem rechtmäßigen vierten Platz. Die resultierenden Ausdrücke für die Basisvariablen nahmen ebenfalls ihre Ordinalstellen ein.
Lassen Sie uns gleich die allgemeine Lösung überprüfen. Der Job ist für Schwarze, aber ich habe ihn bereits gemacht, also fang ihn an =)
Wir setzen drei Helden , , in die linke Seite jeder Gleichung des Systems ein:




Man erhält die entsprechenden rechten Seiten der Gleichungen und somit ist die allgemeine Lösung korrekt gefunden.
Nun zur gefundenen allgemeinen Lösung ![]() wir erhalten zwei besondere Lösungen. Die einzige freie Variable ist hier der Koch. Sie müssen sich nicht den Kopf zerbrechen.
wir erhalten zwei besondere Lösungen. Die einzige freie Variable ist hier der Koch. Sie müssen sich nicht den Kopf zerbrechen.
Dann lass es sein ![]() – private Lösung.
– private Lösung.
Dann lass es sein ![]() – eine weitere private Lösung.
– eine weitere private Lösung.
Antwort: Gemeinsame Entscheidung: ![]() , private Lösungen:
, private Lösungen: ![]() , .
, .
Ich hätte mich nicht an Schwarze erinnern sollen... ...denn mir kamen alle möglichen sadistischen Motive in den Sinn und ich erinnerte mich an das berühmte Photoshop, in dem Ku-Klux-Klans-Mitglieder in weißen Gewändern über das Spielfeld einem schwarzen Fußballspieler nachlaufen. Ich sitze da und lächle ruhig. Du weißt, wie ablenkend...
Vieles in der Mathematik ist schädlich, deshalb ein ähnliches abschließendes Beispiel, wie man es selbst lösen kann.
Beispiel 6
Finden Sie die allgemeine Lösung des linearen Gleichungssystems. 
Ich habe die allgemeine Lösung bereits überprüft, der Antwort kann man vertrauen. Ihre Lösung kann von meiner Lösung abweichen, Hauptsache, die allgemeinen Lösungen stimmen überein.
Wahrscheinlich haben viele Leute einen unangenehmen Moment in den Lösungen bemerkt: Sehr oft mussten wir im umgekehrten Verlauf der Gaußschen Methode mit gewöhnlichen Brüchen herumbasteln. In der Praxis ist dies tatsächlich der Fall; Fälle, in denen es keine Brüche gibt, sind viel seltener. Seien Sie mental und vor allem technisch vorbereitet.
Ich werde auf einige Merkmale der Lösung eingehen, die in den gelösten Beispielen nicht gefunden wurden.
Die allgemeine Lösung des Systems kann manchmal eine Konstante (oder Konstanten) enthalten, zum Beispiel: . Hier ist eine der Grundvariablen gleich einer konstanten Zahl: . Daran ist nichts Exotisches, es passiert. Offensichtlich wird in diesem Fall jede einzelne Lösung an erster Stelle eine Fünf enthalten.
Selten, aber es gibt Systeme, in denen Die Anzahl der Gleichungen ist größer als die Anzahl der Variablen. Die Gaußsche Methode funktioniert unter den schwierigsten Bedingungen; man sollte die erweiterte Matrix des Systems ruhig mit einem Standardalgorithmus auf eine schrittweise Form reduzieren. Ein solches System kann inkonsistent sein, unendlich viele Lösungen haben und seltsamerweise nur eine einzige Lösung haben.
Die Gaußsche Methode, auch Methode der sequentiellen Eliminierung von Unbekannten genannt, lautet wie folgt. Durch elementare Transformationen wird ein lineares Gleichungssystem in eine solche Form gebracht, dass sich seine Koeffizientenmatrix als ergibt trapezförmig (das Gleiche wie dreieckig oder gestuft) oder nahezu trapezförmig (direkter Strich der Gaußschen Methode, im Folgenden einfach gerader Strich). Ein Beispiel für ein solches System und seine Lösung finden Sie in der Abbildung oben.
In einem solchen System enthält die letzte Gleichung nur eine Variable und ihr Wert kann eindeutig ermittelt werden. Der Wert dieser Variablen wird dann in die vorherige Gleichung eingesetzt ( Umkehrung der Gaußschen Methode , dann genau umgekehrt), aus der die vorherige Variable gefunden wird, und so weiter.
In einem trapezförmigen (dreieckigen) System enthält die dritte Gleichung, wie wir sehen, keine Variablen mehr j Und X, und die zweite Gleichung ist die Variable X .
Nachdem die Matrix des Systems eine trapezförmige Form angenommen hat, ist es nicht mehr schwer, die Frage der Kompatibilität des Systems zu verstehen, die Anzahl der Lösungen zu bestimmen und die Lösungen selbst zu finden.
Vorteile der Methode:
- Bei der Lösung linearer Gleichungssysteme mit mehr als drei Gleichungen und Unbekannten ist die Gauß-Methode nicht so umständlich wie die Cramer-Methode, da die Lösung mit der Gauß-Methode weniger Berechnungen erfordert;
- die Gauß-Methode kann unbestimmte Systeme linearer Gleichungen lösen, das heißt, sie haben eine allgemeine Lösung (und wir werden sie in dieser Lektion analysieren), und mit der Cramer-Methode können wir nur sagen, dass das System unbestimmt ist;
- Sie können lineare Gleichungssysteme lösen, in denen die Anzahl der Unbekannten nicht gleich der Anzahl der Gleichungen ist (wir werden sie in dieser Lektion auch analysieren);
- Die Methode basiert auf elementaren (Schul-)Methoden – der Methode zum Ersetzen von Unbekannten und der Methode zum Addieren von Gleichungen, die wir im entsprechenden Artikel angesprochen haben.
Damit jeder die Einfachheit versteht, mit der trapezförmige (dreieckige, stufenförmige) Systeme linearer Gleichungen gelöst werden, präsentieren wir eine Lösung für ein solches System mithilfe der Rückwärtsbewegung. Eine schnelle Lösung für dieses System wurde im Bild zu Beginn der Lektion gezeigt.
Beispiel 1. Lösen Sie ein System linearer Gleichungen mit der Umkehrung:
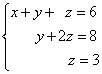
Lösung. In diesem trapezförmigen System ist die Variable z kann eindeutig aus der dritten Gleichung gefunden werden. Wir setzen seinen Wert in die zweite Gleichung ein und erhalten den Wert der Variablen j:
Jetzt kennen wir die Werte zweier Variablen - z Und j. Wir setzen sie in die erste Gleichung ein und erhalten den Wert der Variablen X:
Aus den vorherigen Schritten schreiben wir die Lösung des Gleichungssystems aus:
![]()
Um ein solches trapezförmiges lineares Gleichungssystem zu erhalten, das wir sehr einfach gelöst haben, ist es notwendig, eine Vorwärtsbewegung zu verwenden, die mit elementaren Transformationen des linearen Gleichungssystems verbunden ist. Es ist auch nicht sehr schwierig.
Elementare Transformationen eines Systems linearer Gleichungen
Indem wir die Schulmethode der algebraischen Addition der Gleichungen eines Systems wiederholten, fanden wir heraus, dass wir zu einer der Gleichungen des Systems eine weitere Gleichung des Systems hinzufügen können und jede der Gleichungen mit einigen Zahlen multipliziert werden kann. Als Ergebnis erhalten wir ein System linearer Gleichungen, das diesem entspricht. Darin enthielt eine Gleichung bereits nur eine Variable, deren Wert wir in andere Gleichungen einsetzen und so zu einer Lösung gelangen. Eine solche Addition ist eine der Arten der elementaren Transformation des Systems. Bei Verwendung der Gaußschen Methode können wir verschiedene Arten von Transformationen verwenden.

Die obige Animation zeigt, wie sich das Gleichungssystem nach und nach in ein trapezförmiges verwandelt. Das heißt, das, was Sie in der allerersten Animation gesehen haben und sich davon überzeugt haben, dass es einfach ist, daraus die Werte aller Unbekannten zu ermitteln. Wie eine solche Transformation durchgeführt wird, und natürlich Beispiele werden weiter unten besprochen.
Beim Lösen linearer Gleichungssysteme mit beliebig vielen Gleichungen und Unbekannten im Gleichungssystem und in der erweiterten Matrix des Systems Kann:
- Zeilen neu anordnen (dies wurde ganz am Anfang dieses Artikels erwähnt);
- Wenn andere Transformationen zu gleichen oder proportionalen Zeilen führen, können diese bis auf eine gelöscht werden.
- „Null“-Zeilen entfernen, in denen alle Koeffizienten gleich Null sind;
- eine beliebige Zeichenfolge mit einer bestimmten Zahl multiplizieren oder dividieren;
- Fügen Sie zu jeder Zeile eine weitere Zeile hinzu, multipliziert mit einer bestimmten Zahl.
Als Ergebnis der Transformationen erhalten wir ein diesem System äquivalentes lineares Gleichungssystem.
Algorithmus und Beispiele zum Lösen eines linearen Gleichungssystems mit einer quadratischen Matrix des Systems mithilfe der Gauß-Methode
Betrachten wir zunächst die Lösung linearer Gleichungssysteme, bei denen die Anzahl der Unbekannten gleich der Anzahl der Gleichungen ist. Die Matrix eines solchen Systems ist quadratisch, das heißt, die Anzahl der Zeilen darin ist gleich der Anzahl der Spalten.
Beispiel 2. Lösen Sie ein lineares Gleichungssystem mit der Gauß-Methode
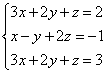
Beim Lösen linearer Gleichungssysteme mit Schulmethoden haben wir eine der Gleichungen Term für Term multipliziert, sodass die Koeffizienten der ersten Variablen in den beiden Gleichungen entgegengesetzte Zahlen waren. Beim Hinzufügen von Gleichungen wird diese Variable eliminiert. Die Gauß-Methode funktioniert ähnlich.
Um das Erscheinungsbild der Lösung zu vereinfachen Lassen Sie uns eine erweiterte Matrix des Systems erstellen:

In dieser Matrix befinden sich die Koeffizienten der Unbekannten links vor der vertikalen Linie und die freien Terme rechts hinter der vertikalen Linie.
Zur Vereinfachung der Division von Koeffizienten für Variablen (um eine Division durch Eins zu erhalten) Lassen Sie uns die erste und zweite Zeile der Systemmatrix vertauschen. Wir erhalten ein zu diesem äquivalentes System, da in einem System linearer Gleichungen die Gleichungen vertauscht werden können:

Verwendung der neuen ersten Gleichung Eliminieren Sie die Variable X aus der zweiten und allen folgenden Gleichungen. Dazu fügen wir zur zweiten Zeile der Matrix die erste Zeile, multipliziert mit (in unserem Fall mit ), zur dritten Zeile hinzu – die erste Zeile, multipliziert mit (in unserem Fall mit ).
Dies ist möglich, weil
Gäbe es mehr als drei Gleichungen in unserem System, müssten wir zu allen nachfolgenden Gleichungen die erste Zeile addieren, multipliziert mit dem Verhältnis der entsprechenden Koeffizienten, mit Minuszeichen versehen.
Als Ergebnis erhalten wir eine zu diesem System äquivalente Matrix eines neuen Gleichungssystems, in der alle Gleichungen, beginnend mit der zweiten, enthalten sind enthalten keine Variable X :

Um die zweite Zeile des resultierenden Systems zu vereinfachen, multiplizieren Sie sie mit und erhalten erneut die Matrix eines diesem System äquivalenten Gleichungssystems:

Wenn wir nun die erste Gleichung des resultierenden Systems unverändert lassen, Mit der zweiten Gleichung eliminieren wir die Variable j aus allen nachfolgenden Gleichungen. Dazu fügen wir zur dritten Zeile der Systemmatrix die zweite Zeile hinzu, multipliziert mit (in unserem Fall mit ).
Gäbe es mehr als drei Gleichungen in unserem System, müssten wir zu allen nachfolgenden Gleichungen eine zweite Zeile hinzufügen, multipliziert mit dem Verhältnis der entsprechenden Koeffizienten mit Minuszeichen.
Als Ergebnis erhalten wir wieder die Matrix eines zu diesem linearen Gleichungssystem äquivalenten Systems:
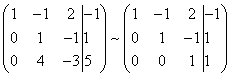
Wir haben ein äquivalentes trapezförmiges System linearer Gleichungen erhalten:
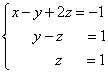
Wenn die Anzahl der Gleichungen und Variablen größer ist als in unserem Beispiel, wird der Prozess der sequentiellen Eliminierung von Variablen fortgesetzt, bis die Systemmatrix trapezförmig wird, wie in unserem Demobeispiel.
Wir werden die Lösung „vom Ende her“ finden – den umgekehrten Schritt. Dafür Aus der letzten Gleichung ermitteln wir z:
.
Setzt man diesen Wert in die vorherige Gleichung ein, wir werden finden j:
Aus der ersten Gleichung wir werden finden X:
![]()
Antwort: Die Lösung dieses Gleichungssystems lautet ![]() .
.
: In diesem Fall wird die gleiche Antwort gegeben, wenn das System eine eindeutige Lösung hat. Wenn das System unendlich viele Lösungen hat, dann ist dies die Antwort, und das ist das Thema des fünften Teils dieser Lektion.
Lösen Sie selbst ein lineares Gleichungssystem mit der Gaußschen Methode und schauen Sie sich dann die Lösung an
Auch hier haben wir ein Beispiel für ein konsistentes und eindeutiges System linearer Gleichungen, bei dem die Anzahl der Gleichungen gleich der Anzahl der Unbekannten ist. Der Unterschied zu unserem Demo-Beispiel des Algorithmus besteht darin, dass es bereits vier Gleichungen und vier Unbekannte gibt.
Beispiel 4. Lösen Sie ein System linearer Gleichungen mit der Gauß-Methode:


Jetzt müssen Sie die zweite Gleichung verwenden, um die Variable aus nachfolgenden Gleichungen zu eliminieren. Lassen Sie uns die vorbereitenden Arbeiten durchführen. Um das Verhältnis der Koeffizienten bequemer zu gestalten, müssen Sie einen in die zweite Spalte der zweiten Zeile eingeben. Subtrahieren Sie dazu die dritte von der zweiten Zeile und multiplizieren Sie die resultierende zweite Zeile mit -1.
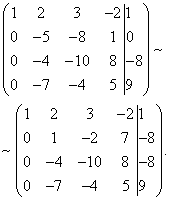
Führen wir nun die eigentliche Eliminierung der Variablen aus der dritten und vierten Gleichung durch. Fügen Sie dazu die zweite Zeile, multipliziert mit , zur dritten Zeile und die zweite, multipliziert mit, zur vierten Zeile hinzu.

Mithilfe der dritten Gleichung eliminieren wir nun die Variable aus der vierten Gleichung. Addieren Sie dazu die dritte Zeile zur vierten Zeile, multipliziert mit . Wir erhalten eine erweiterte Trapezmatrix.

Wir haben ein Gleichungssystem erhalten, zu dem das gegebene System äquivalent ist:

Folglich sind die resultierenden und gegebenen Systeme kompatibel und eindeutig. Wir finden die endgültige Lösung „vom Ende her“. Aus der vierten Gleichung können wir den Wert der Variablen „x-vier“ direkt ausdrücken:
Wir setzen diesen Wert in die dritte Gleichung des Systems ein und erhalten
![]() ,
,
![]() ,
,
Zum Schluss noch die Wertsubstitution
Die erste Gleichung ergibt
![]() ,
,
Wo finden wir „x zuerst“:
Antwort: Dieses Gleichungssystem hat eine eindeutige Lösung ![]() .
.
Sie können die Lösung des Systems auch mit der Cramer-Methode auf einem Taschenrechner überprüfen: In diesem Fall wird die gleiche Antwort gegeben, wenn das System eine eindeutige Lösung hat.
Lösung angewandter Probleme mit der Gauß-Methode am Beispiel einer Legierungsaufgabe
Systeme linearer Gleichungen werden zur Modellierung realer Objekte in der physischen Welt verwendet. Lösen wir eines dieser Probleme – Legierungen. Ähnliche Probleme betreffen Mischungen, die Kosten oder den Anteil einzelner Güter an einer Gütergruppe und dergleichen.
Beispiel 5. Drei Legierungsstücke haben eine Gesamtmasse von 150 kg. Die erste Legierung enthält 60 % Kupfer, die zweite 30 % und die dritte 10 %. Darüber hinaus sind in der zweiten und dritten Legierung zusammen 28,4 kg weniger Kupfer enthalten als in der ersten Legierung und in der dritten Legierung sind 6,2 kg weniger Kupfer enthalten als in der zweiten. Ermitteln Sie die Masse jedes einzelnen Legierungsstücks.
Lösung. Wir stellen ein System linearer Gleichungen auf:

Multiplizieren wir die zweite und dritte Gleichung mit 10, erhalten wir ein äquivalentes System linearer Gleichungen:
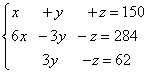
Wir erstellen eine erweiterte Matrix des Systems:

Achtung, geradeaus. Durch Addition (in unserem Fall Subtraktion) einer Zeile multipliziert mit einer Zahl (wir wenden sie zweimal an) ergeben sich die folgenden Transformationen mit der erweiterten Matrix des Systems:

Der direkte Umzug ist beendet. Wir haben eine erweiterte Trapezmatrix erhalten.
Wir wenden den umgekehrten Zug an. Wir finden die Lösung vom Ende her. Wir sehen das.
Aus der zweiten Gleichung finden wir
Aus der dritten Gleichung -
Sie können die Lösung des Systems auch mit der Cramer-Methode auf einem Taschenrechner überprüfen: In diesem Fall wird die gleiche Antwort gegeben, wenn das System eine eindeutige Lösung hat.
Die Einfachheit der Gauß-Methode zeigt sich daran, dass der deutsche Mathematiker Carl Friedrich Gauß nur 15 Minuten brauchte, um sie zu erfinden. Neben der nach ihm benannten Methode ist aus den Werken von Gauß das Sprichwort „Wir sollten das Unglaubliche und Unnatürliche nicht mit dem absolut Unmöglichen verwechseln“ bekannt – eine Art kurze Anleitung zum Entdecken.
In vielen angewandten Problemen gibt es möglicherweise keine dritte Nebenbedingung, also keine dritte Gleichung, dann muss man ein System aus zwei Gleichungen mit drei Unbekannten mit der Gaußschen Methode lösen, oder umgekehrt gibt es weniger Unbekannte als Gleichungen. Wir beginnen nun mit der Lösung solcher Gleichungssysteme.
Mit der Gaußschen Methode können Sie feststellen, ob ein System kompatibel oder inkompatibel ist N lineare Gleichungen mit N Variablen.
Die Gauß-Methode und lineare Gleichungssysteme mit unendlich vielen Lösungen
Das nächste Beispiel ist ein konsistentes, aber unbestimmtes System linearer Gleichungen, das heißt mit unendlich vielen Lösungen.
Nach der Durchführung von Transformationen in der erweiterten Matrix des Systems (Zeilen neu anordnen, Zeilen mit einer bestimmten Zahl multiplizieren und dividieren, einer Zeile eine weitere hinzufügen) könnten Zeilen der Form erscheinen
Wenn in allen Gleichungen die Form
Freie Terme sind gleich Null, das bedeutet, dass das System unbestimmt ist, also unendlich viele Lösungen hat, und Gleichungen dieser Art sind „überflüssig“ und wir schließen sie aus dem System aus.
Beispiel 6.
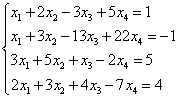
Lösung. Lassen Sie uns eine erweiterte Matrix des Systems erstellen. Anschließend eliminieren wir die Variable mithilfe der ersten Gleichung aus den nachfolgenden Gleichungen. Fügen Sie dazu zur zweiten, dritten und vierten Zeile die erste hinzu, multipliziert mit:

Fügen wir nun die zweite Zeile zur dritten und vierten hinzu.

Als Ergebnis kommen wir zum System

Die letzten beiden Gleichungen wurden zu Gleichungen der Form. Diese Gleichungen sind für jeden Wert der Unbekannten erfüllt und können verworfen werden.
Um die zweite Gleichung zu erfüllen, können wir beliebige Werte für und wählen, dann wird der Wert für eindeutig bestimmt: ![]() . Aus der ersten Gleichung ergibt sich auch eindeutig der Wert für:
. Aus der ersten Gleichung ergibt sich auch eindeutig der Wert für: ![]() .
.
Sowohl das angegebene als auch das letzte System sind konsistent, aber unsicher, und die Formeln

für beliebig und geben uns alle Lösungen eines gegebenen Systems.
Gauß-Methode und lineare Gleichungssysteme ohne Lösungen
Das nächste Beispiel ist ein inkonsistentes System linearer Gleichungen, also eines, das keine Lösungen hat. Die Antwort auf solche Probleme lässt sich so formulieren: Das System hat keine Lösungen.
Wie bereits im Zusammenhang mit dem ersten Beispiel erwähnt, könnten nach der Durchführung von Transformationen Zeilen des Formulars in der erweiterten Matrix des Systems erscheinen
entsprechend einer Gleichung der Form
Wenn es unter ihnen mindestens eine Gleichung mit einem freien Term ungleich Null gibt (d. h. ), dann ist dieses Gleichungssystem inkonsistent, das heißt, es hat keine Lösungen und seine Lösung ist vollständig.
Beispiel 7. Lösen Sie das lineare Gleichungssystem mit der Gauß-Methode:

Lösung. Wir erstellen eine erweiterte Matrix des Systems. Mithilfe der ersten Gleichung schließen wir die Variable aus nachfolgenden Gleichungen aus. Addieren Sie dazu die erste Zeile multipliziert mit der zweiten Zeile, die erste Zeile multipliziert mit der dritten Zeile und die erste Zeile multipliziert mit der vierten Zeile.

Jetzt müssen Sie die zweite Gleichung verwenden, um die Variable aus nachfolgenden Gleichungen zu eliminieren. Um ganzzahlige Koeffizientenverhältnisse zu erhalten, vertauschen wir die zweite und dritte Zeile der erweiterten Matrix des Systems.

Um die dritte und vierte Gleichung auszuschließen, addieren Sie die zweite Gleichung multipliziert mit , zur dritten Zeile und die zweite multipliziert mit , zur vierten Zeile.

Mithilfe der dritten Gleichung eliminieren wir nun die Variable aus der vierten Gleichung. Addieren Sie dazu die dritte Zeile zur vierten Zeile, multipliziert mit .

Das gegebene System entspricht daher dem Folgenden:

Das resultierende System ist inkonsistent, da seine letzte Gleichung durch keine Werte der Unbekannten erfüllt werden kann. Daher gibt es für dieses System keine Lösungen.
Die Wahrung Ihrer Privatsphäre ist uns wichtig. Aus diesem Grund haben wir eine Datenschutzrichtlinie entwickelt, die beschreibt, wie wir Ihre Daten verwenden und speichern. Bitte lesen Sie unsere Datenschutzpraktiken durch und teilen Sie uns mit, wenn Sie Fragen haben.
Erhebung und Nutzung personenbezogener Daten
Unter personenbezogenen Daten versteht man Daten, die dazu genutzt werden können, eine bestimmte Person zu identifizieren oder mit ihr in Kontakt zu treten.
Sie können jederzeit um die Angabe Ihrer persönlichen Daten gebeten werden, wenn Sie mit uns Kontakt aufnehmen.
Nachfolgend finden Sie einige Beispiele für die Arten personenbezogener Daten, die wir möglicherweise sammeln, und wie wir diese Informationen verwenden können.
Welche personenbezogenen Daten erfassen wir:
- Wenn Sie auf der Website eine Bewerbung einreichen, erfassen wir möglicherweise verschiedene Informationen, einschließlich Ihres Namens, Ihrer Telefonnummer, Ihrer E-Mail-Adresse usw.
Wie wir Ihre persönlichen Daten verwenden:
- Die von uns erfassten personenbezogenen Daten ermöglichen es uns, Sie mit einzigartigen Angeboten, Werbeaktionen und anderen Veranstaltungen sowie bevorstehenden Veranstaltungen zu kontaktieren.
- Von Zeit zu Zeit können wir Ihre persönlichen Daten verwenden, um wichtige Mitteilungen und Mitteilungen zu versenden.
- Wir können personenbezogene Daten auch für interne Zwecke verwenden, beispielsweise zur Durchführung von Audits, Datenanalysen und verschiedenen Forschungsarbeiten, um die von uns bereitgestellten Dienste zu verbessern und Ihnen Empfehlungen zu unseren Diensten zu geben.
- Wenn Sie an einer Verlosung, einem Wettbewerb oder einer ähnlichen Aktion teilnehmen, können wir die von Ihnen bereitgestellten Informationen zur Verwaltung solcher Programme verwenden.
Weitergabe von Informationen an Dritte
Wir geben die von Ihnen erhaltenen Informationen nicht an Dritte weiter.
Ausnahmen:
- Wenn es erforderlich ist – in Übereinstimmung mit dem Gesetz, dem Gerichtsverfahren, in Gerichtsverfahren und/oder auf der Grundlage öffentlicher Anfragen oder Anfragen von Regierungsstellen in der Russischen Föderation – Ihre personenbezogenen Daten offenzulegen. Wir können auch Informationen über Sie offenlegen, wenn wir zu dem Schluss kommen, dass eine solche Offenlegung aus Sicherheits-, Strafverfolgungs- oder anderen Gründen von öffentlicher Bedeutung notwendig oder angemessen ist.
- Im Falle einer Umstrukturierung, Fusion oder eines Verkaufs können wir die von uns erfassten personenbezogenen Daten an den jeweiligen Nachfolger-Dritten weitergeben.
Schutz personenbezogener Daten
Wir treffen Vorkehrungen – einschließlich administrativer, technischer und physischer –, um Ihre persönlichen Daten vor Verlust, Diebstahl und Missbrauch sowie vor unbefugtem Zugriff, Offenlegung, Änderung und Zerstörung zu schützen.
Respektieren Sie Ihre Privatsphäre auf Unternehmensebene
Um sicherzustellen, dass Ihre persönlichen Daten sicher sind, kommunizieren wir Datenschutz- und Sicherheitsstandards an unsere Mitarbeiter und setzen Datenschutzpraktiken strikt durch.




