Permyakova Yulia

The theme of my project is “Floating Bodies.”

Goal of the work : studying Archimedes' law, finding out the conditions and features of floating bodies, testing them in experiments.

Download:

Preview:

Municipal Educational Institution "Security School s. Dorogovinovka, Pugachevsky district, Saratov region"

PROJECT

in physics

on the topic “Floating bodies”

7th grade student

Municipal educational institution of secondary school s. Dorogovinovka

Permyakova Yulia Teacher: Konnova I.V.

S. Dorogovinovka

year 2014

I. Introduction

The theme of my project is “Floating Bodies.”

Goal of the work : studying Archimedes' law, finding out the conditions and features of floating bodies, testing them in experiments.

Tasks:

1. Select and study literature on the topic.
2. Tell about the history of the discovery of Archimedes' law.
3. Prove the existence of Archimedean force.
4. Test the floating conditions of bodies through experiments.

II. MAIN PART

1. Theoretical part

1.1. About Archimedes

Archimedes was born in the Greek city of Syracuse in 287 BC. e., where he lived almost his entire life, and where he was engaged in scientific activities. He studied first with his father, the astronomer and mathematician Phidias, then in Alexandria, where the rulers of Egypt gathered the best Greek scientists and thinkers, and also founded the famous, largest library in the world. Here, in Alexandria, Archimedes met the students of Euclid, with whom he maintained a lively correspondence throughout his life. Here he intensively studied the works of Democritus, Eudoxus and other scientists.

After studying in Alexandria, Archimedes returned to Syracuse and inherited the position of his father, court astronomer.

In theoretical terms, the work of this great scientist was dazzlingly multifaceted. Archimedes' main works concerned various practical applications of mathematics (geometry), physics, hydrostatics and mechanics. He was also an inventive engineer who used his talent to solve a number of practical problems.

Thirteen treatises of Archimedes have reached us. In the most famous of them, “On the Sphere and the Cylinder” (in two books), Archimedes establishes that the surface area of ​​a sphere is 4 times the area of ​​its largest cross-section. Archimedes' work consists of calculations of the areas of figures bounded by curves and the volumes of bodies bounded by arbitrary planes - so Archimedes can rightly be considered the father of integral calculus, which arose two millennia later.

They say that Archimedes considered his most important discovery to be the proof that the volume of a sphere and the cylinder circumscribed around it are related to each other as 2:3. Archimedes asked his friends to place this evidence on his tombstone.

Archimedes also tried to solve the problem of squaring a circle and achieved outstanding results in this, combining them into the work “On the Measurement of a Circle”:

1. The area of ​​a circle is equal to the area of ​​a right triangle with legs equal to the length and radius of the circle (πr 2 ).

2. The area of ​​a circle is related to the area of ​​the square circumscribed around it as 11:14.

3. The ratio of circumference to diameter is greater and less.

Archimedes was the first to calculate the number “pi” - the ratio of the circumference to the diameter - and proved that it is the same for any circle.

Archimedes also found the sum to be infinitegeometric progression with denominator . In mathematics this was the first example of infinity row.

While studying a problem that reduced to a cubic equation, Archimedes discovered the role of the characteristic, which was later called the discriminant.

Archimedes had a formula for determining the area of ​​a triangle through its three sides (incorrectly called Heron's formula).

A major role in the development of mathematics was played by his essay “Psammit” - “On the number of grains of sand”, in which he shows how, using the existing number systemYou can express arbitrarily large numbers. As a basis for his reasoning, he uses the problem of counting the number of grains of sand within the visible Universe. Thus, the then existing opinion about the presence of mysterious “largest numbers” was refuted" We still use the system of naming integers invented by Archimedes.

The listed scientific discoveries are only a small part of Archimedes' work. It was diligently translated and commented on by Arabs, and then by Western European scientists.

In physics, Archimedes introduced the concept of the center of gravity, established the scientific principles of statics and hydrostatics, and gave examples of the use of mathematical methods in physical research. The basic principles of statics are formulated in the essay “On the Equilibrium of Plane Figures.” Archimedes considers the addition of parallel forces, defines the concept of the center of gravity for various figures, and gives a derivation of the law of leverage. The famous law of hydrostatics, which entered science with his name (Archimedes' law), was formulated in the treatise “On Floating Bodies”.

He is credited with the famous expression: “Give me a fulcrum and I will move the earth.” Apparently, it was expressed in connection with the descent of the ship"Siracosia" to the water. The workers were unable to move this ship. They were helped by Archimedes, who created a system of blocks (pulley hoist), with the help of which one person, the king himself, accomplished this work.

1.2. Archimedes' Law

According to legend, the kingHiero instructed Archimedes to check whether his crown was made of pure gold or whether the jeweler had appropriated part of the gold by alloying it with silver. While pondering this problem, Archimedes once went into a bathhouse and there, plunging into the bath, he noticed that the amount of water overflowing was equal to the amount of water displaced by his body. This observation prompted Archimedes to solve the problem of the crown, and he, without hesitating a second, jumped out of the bath and, as if he were naked, rushed home, shouting at the top of his voice about his discovery: “Eureka! Eureka!" (Greek: “Found! Found!”).”

The fact that a certain force acts on a body immersed in water is well known to everyone: heavy bodies seem to become lighter - for example, our own body when immersed in a bath. When swimming in a river or sea, you can easily lift and move very heavy stones along the bottom - those that cannot be lifted on land; the same phenomenon is observed when, for some reason, a whale is washed up on the shore - the animal cannot move outside the aquatic environment - its weight exceeds the capabilities of its muscular system. At the same time, lightweight bodies resist immersion in water: sinking a ball the size of a small watermelon requires both strength and dexterity; It will most likely not be possible to immerse a ball with a diameter of half a meter. It is intuitively clear that the answer to the question - why a body floats (and another sinks) is closely related to the effect of the liquid on the body immersed in it; one cannot be satisfied with the answer that light bodies float and heavy ones sink: a steel plate, of course, will sink in water, but if you make a box out of it, then it can float; however, her weight will not change.

To understand the nature of the force acting from a liquid on a submerged body, it is enough to consider a simple example (Fig. 1).

The cube is immersed in water, and both the water and the cube are motionless. It is known that the pressure in a heavy liquid increases in proportion to depth - it is obvious that a higher column of liquid presses more strongly on the base. This pressure acts not only downwards, but also sideways and upwards with the same intensity - this is Pascal's law.

If we consider the forces acting on the cube (Fig. 1), then due to the obvious symmetry, the forces acting on the opposite side faces are equal and oppositely directed - they try to compress the cube, but cannot affect its balance or movement. The forces acting on the upper and lower faces remain. Since the pressure at depth is greater than at the surface of the liquid and, and , then > . Since the forces F 2 and F 1 are directed in opposite directions, then their resultant is equal to the difference F 2 – F 1 and is directed in the direction of greater force, that is, upward. This resultant is the Archimedean force, that is, the force that pushes the body out of the liquid.

Archimedes' Law

Archimedes' law is formulated as follows:a body located in a liquid (or gas) loses as much weight as the liquid (or gas) weighs in the volume displaced by the body.

1.3. What does buoyant force depend on?

The behavior of a body in a liquid depends on the relationship between the gravity modules F T and Archimedean force F A that act on this body. The following three cases are possible:

1. F t > F A – the body drowns;
2. F t = F A – a body floats in a liquid;
3. F t A – the body floats up until it begins to float on the surface of the liquid.

Also, the behavior of a body in a liquid depends on the ratio of the densities of the body and the liquid. Therefore, to determine the behavior of a body in a liquid, we can compare the densitiesbodies and liquids. In this case, three situations are also possible:

1. ρ of the body > ρ of the liquid – the body sinks
2. ρ body = ρ liquid – the body floats
3. body ρ liquids - the body floats up.

Let's give examples.

Iron density – 7800 kg/m 3 , water density – 1000 kg/m 3 . This means that a piece of iron will sink in water. Ice density – 900 kg/m 3 , water density – 1000 kg/m 3 , so ice does not sink in water, and if you throw it into water, it will begin to float and float on the surface.

2. Practical part

2.1. Proof of the existence of Archimedean force

Let's conduct an experiment: take a cylinder suspended from a dynamometer and measure the weight of this cylinder. Let's immerse it in a vessel with water. Let's weigh it again. We noticed that the weight of the cylinder became lighter.

Let's repeat the experiment with another body - a bunch of keys. The weight of the bundle immersed in water again became less.

Conclusion: any body immersed in a liquid is subject to a buoyant force called the Archimedean force.

2.2. Calculation of Archimedean force

Let's calculate the buoyant force.

To do this, let's measure the weight of a body in the air, then measure the weight of the same body, but completely immersed in water. The difference between these forces will be the value of the Archimedean force.

F A = ​​P in air. – P in water.

Otherwise, the Archimedean force can be calculated by knowing the density of the liquid and the volume of the body immersed in this liquid, using the formula:

F A = ​​g ρ f V t

2.3. Comparison of gravity and Archimedean force

Let's conduct an experiment.

Let's take a body - a bubble with a certain amount of sand. Let us determine the force of gravity and the Archimedean force acting on this body. Let's compare them. We see that if:

F t > F A – the body drowns;

F t = F A – a body floats in a liquid;

F t A – the body floats up

Conclusion: the behavior of a body in a liquid depends on the relationship between the gravity modules F T and Archimedean force F A that act on this body.

2.4 Comparison of densities of liquid and body

Let's do one more experiment. Let us take bodies whose densities are less or greater than the density of water. Let's immerse them in water. We will see that“bodies that are heavier than a liquid, being lowered into it, sink deeper and deeper until they reach the bottom, and, while in the liquid, lose as much in their weight as the liquid weighs, taken in the volume of the bodies,” -as Archimedes said.

Conclusion: the behavior of a body in a liquid depends on the ratio of the densities of the body and the liquid.

2.5 Comparison of the Archimedean force acting on a body in liquids of different densities

Let's conduct an experiment: take two liquids of different densities: shampoo and fresh water, and a piece of plasticine. Let us determine the buoyancy force acting on plasticinefrom each of the liquids. We will see that the Archimedean force turned out to be different: for a liquid with a higher density (shampoo) it is greater than for a liquid with a lower density (fresh water).

The text of the work is posted without images and formulas.
The full version of the work is available in the "Work Files" tab in PDF format

Introduction

Relevance: If you take a close look at the world around you, you can discover many events happening around you. Since ancient times, man has been surrounded by water. When we swim in it, our body pushes some forces to the surface. I have long asked myself the question: “Why do bodies float or sink? Does water push things out?

My research work is aimed at deepening the knowledge gained in class about Archimedean force. Answer the questions that interest me, using life experience, observations of the surrounding reality, conduct my own experiments and explain their results, which will expand my knowledge on this topic. All sciences are interconnected. And the common object of study of all sciences is man “plus” nature. I am sure that the study of the action of Archimedean force is relevant today.

Hypothesis: I assume that at home you can calculate the magnitude of the buoyancy force acting on a body immersed in a liquid and determine whether it depends on the properties of the liquid, the volume and shape of the body.

Object of study: Buoyancy force in liquids.

Tasks:

Study the history of the discovery of Archimedean force;

Study educational literature on the action of Archimedean force;

Develop skills in conducting independent experiments;

Prove that the value of the buoyant force depends on the density of the liquid.

Research methods:

Research;

Calculated;

Information search;

Observations

1. Discovery of Archimedes' power

There is a famous legend about how Archimedes ran down the street and shouted “Eureka!” This just tells the story of his discovery that the buoyant force of water is equal in magnitude to the weight of the water displaced by it, the volume of which is equal to the volume of the body immersed in it. This discovery is called Archimedes' law.

In the 3rd century BC, there lived Hiero, the king of the ancient Greek city of Syracuse, and he wanted to make himself a new crown from pure gold. I measured it exactly as needed and gave the order to the jeweler. A month later, the master returned the gold in the form of a crown and it weighed as much as the mass of the given gold. But anything can happen, and the master could have cheated by adding silver or, even worse, copper, because you can’t tell the difference by eye, but the mass is what it should be. And the king wants to know: was the work done honestly? And then, he asked the scientist Archimedes to check whether the master made his crown from pure gold. As is known, the mass of a body is equal to the product of the density of the substance from which the body is made and its volume: . If different bodies have the same mass, but they are made of different substances, then they will have different volumes. If the master had returned to the king not a jewelry-made crown, the volume of which is impossible to determine due to its complexity, but a piece of metal of the same shape that the king gave him, then it would have been immediately clear whether he had mixed another metal into it or not. And while taking a bath, Archimedes noticed that water was pouring out of it. He suspected that it was pouring out in exactly the volume that his body parts immersed in water occupied. And it dawned on Archimedes that the volume of the crown can be determined by the volume of water displaced by it. Well, if you can measure the volume of the crown, then it can be compared with the volume of a piece of gold of equal mass. Archimedes immersed the crown in water and measured how the volume of water increased. He also immersed a piece of gold in water, the mass of which was the same as that of the crown. And then he measured how the volume of water increased. The volumes of water displaced in the two cases turned out to be different. Thus, the master was exposed as a deceiver, and science was enriched with a remarkable discovery.

It is known from history that the problem of the golden crown prompted Archimedes to study the question of the floating of bodies. The experiments carried out by Archimedes were described in the essay “On Floating Bodies,” which has come down to us. The seventh sentence (theorem) of this work was formulated by Archimedes as follows: bodies heavier than the liquid, immersed in this liquid, will sink until they reach the very bottom, and in the liquid they will become lighter by the weight of the liquid in a volume equal to the volume of the immersed body.

It is interesting that the Archimedes force is zero when a body immersed in a liquid is tightly pressed to the bottom with its entire base.

The discovery of the fundamental law of hydrostatics is the greatest achievement of ancient science.

2. Formulation and explanation of Archimedes' law

Archimedes' law describes the effect of liquids and gases on a body immersed in them, and is one of the main laws of hydrostatics and gas statics.

Archimedes' law is formulated as follows: a body immersed in a liquid (or gas) is acted upon by a buoyant force equal to the weight of the liquid (or gas) in the volume of the immersed part of the body - this force is called by the power of Archimedes:

,

where is the density of the liquid (gas), is the acceleration of gravity, is the volume of the submerged part of the body (or the part of the volume of the body located below the surface).

Consequently, the Archimedean force depends only on the density of the liquid in which the body is immersed and on the volume of this body. But it does not depend, for example, on the density of the substance of a body immersed in a liquid, since this quantity is not included in the resulting formula.

It should be noted that the body must be completely surrounded by liquid (or intersect with the surface of the liquid). So, for example, Archimedes' law cannot be applied to a cube that lies at the bottom of a tank, hermetically touching the bottom.

3. Definition of Archimedes' force

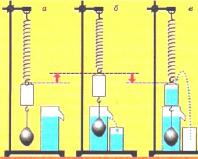
The force with which a body in a liquid is pushed by it can be determined experimentally using this device:

We hang a small bucket and a cylindrical body on a spring fixed to a tripod. We mark the stretch of the spring with an arrow on a tripod, showing the weight of the body in the air. Having lifted the body, we place a glass with a drainage tube under it, filled with liquid to the level of the drainage tube. After which the body is immersed entirely in liquid. In this case, part of the liquid, the volume of which is equal to the volume of the body, is poured from the casting vessel into the glass. The spring pointer rises and the spring contracts, indicating a decrease in body weight in the liquid. In this case, along with the force of gravity, the body is also acted upon by a force that pushes it out of the liquid. If liquid from a glass is poured into the bucket (i.e., the liquid that was displaced by the body), then the spring pointer will return to its initial position.

Based on this experiment, we can conclude that the force pushing out a body completely immersed in a liquid is equal to the weight of the liquid in the volume of this body. The dependence of pressure in a liquid (gas) on the depth of immersion of a body leads to the appearance of a buoyant force (Archimedes' force) acting on any body immersed in a liquid or gas. When a body dives, it moves downward under the influence of gravity. The Archimedean force is always directed opposite to the force of gravity, therefore the weight of a body in a liquid or gas is always less than the weight of this body in a vacuum.

This experiment confirms that the Archimedean force is equal to the weight of the liquid in the volume of the body.

4. Condition of floating bodies

A body located inside a liquid is acted upon by two forces: the force of gravity, directed vertically downward, and the Archimedean force, directed vertically upward. Let us consider what will happen to the body under the influence of these forces if at first it was motionless.

In this case, three cases are possible:

1) If the force of gravity is greater than the Archimedean force, then the body goes down, that is, it sinks:

, then the body drowns;

2) If the modulus of gravity is equal to the modulus of Archimedean force, then the body can be in equilibrium inside the liquid at any depth:

, then the body floats;

3) If the Archimedean force is greater than the force of gravity, then the body will rise from the liquid - float:

, then the body floats.

If a floating body partially protrudes above the surface of the liquid, then the volume of the immersed part of the floating body is such that the weight of the displaced liquid is equal to the weight of the floating body.

Archimedean force is greater than gravity if the density of the liquid is greater than the density of the body immersed in the liquid, if

1) =— a body floats in a liquid or gas, 2) >—the body drowns, 3) < — тело всплывает до тех пор, пока не начнет плавать.

It is these principles of the relationship between gravity and Archimedes’ force that are used in shipping. However, huge river and sea vessels made of steel, the density of which is almost 8 times greater than the density of water, float on the water. This is explained by the fact that only a relatively thin hull of the vessel is made of steel, and most of its volume is occupied by air. The average density of the ship turns out to be significantly less than the density of water; therefore, it not only does not sink, but can also accept a large amount of cargo for transportation. Vessels that navigate rivers, lakes, seas and oceans are built from different materials with different densities. The hull of ships is usually made of steel sheets. All internal fastenings that give ships strength are also made of metals. To build ships, different materials are used, which have both higher and lower density compared to water. The weight of water displaced by the underwater part of the vessel is equal to the weight of the vessel with the cargo in the air or the force of gravity acting on the vessel with the cargo.

For aeronautics, balloons were first used, which were previously filled with heated air, now with hydrogen or helium. In order for the ball to rise into the air, it is necessary that the Archimedean force (buoyancy) acting on the ball be greater than the force of gravity.

5. Conducting the experiment

Investigate the behavior of a raw egg in various types of liquids.

Objective: to prove that the value of the buoyant force depends on the density of the liquid.

I took one raw egg and various kinds of liquids (Appendix 1):

The water is clean;

Water saturated with salt;

Sunflower oil.

First, I lowered the raw egg into clean water - the egg sank - “sank to the bottom” (Appendix 2). Then I added a tablespoon of table salt to a glass of clean water, as a result the egg floats (Appendix 3). And finally, I lowered the egg into a glass with sunflower oil - the egg sank to the bottom (Appendix 4).

Conclusion: in the first case, the density of the egg is greater than the density of water and therefore the egg sank. In the second case, the density of salt water is greater than the density of the egg, so the egg floats in the liquid. In the third case, the density of the egg is also greater than the density of sunflower oil, so the egg sank. Therefore, the greater the density of the liquid, the less the force of gravity.

2. The action of Archimedean force on the human body in water.

Determine the density of the human body experimentally, compare it with the density of fresh and sea water and draw a conclusion about the fundamental ability of a person to swim;

Calculate the weight of a person in the air and the Archimedean force acting on a person in water.

First, I measured my body weight using a scale. Then he measured the volume of the body (without the volume of the head). To do this, I poured enough water into the bath so that when I immersed myself in the water, I was completely submerged (except for my head). Next, using a centimeter tape, I marked the distance from the top edge of the bath to the water level ℓ 1, and then when immersed in water ℓ 2. After that, using a pre-graduated three-liter jar, I began to pour water into the bath from level ℓ 1 to level ℓ 2 - this is how I measured the volume of water I displaced (Appendix 5). I calculated the density using the formula:

The force of gravity acting on a body in the air was calculated using the formula: , where is the acceleration of gravity ≈ 10. The value of the buoyancy force was calculated using the formula described in paragraph 2.

Conclusion: The human body is denser than fresh water, which means it drowns in it. It is easier for a person to swim in the sea than in a river, since the density of sea water is greater, and therefore the buoyant force is greater.

Conclusion

In the process of working on this topic, we learned a lot of new and interesting things. The range of our knowledge has increased not only in the field of action of Archimedes’ power, but also in its application in life. Before starting work, we had a far from detailed idea about it. During the experiments, we experimentally confirmed the validity of Archimedes' law and found out that the buoyancy force depends on the volume of the body and the density of the liquid; the higher the density of the liquid, the greater the Archimedean force. The resulting force, which determines the behavior of a body in a liquid, depends on the mass, volume of the body and the density of the liquid.

In addition to the experiments performed, additional literature was studied about the discovery of Archimedes' force, about the floating of bodies, and aeronautics.

Each of you can make amazing discoveries, and for this you do not need to have any special knowledge or powerful equipment. We just need to look a little more carefully at the world around us, be a little more independent in our judgments, and discoveries will not keep you waiting. The reluctance of most people to explore the world around them leaves a lot of scope for the curious in the most unexpected places.

Bibliography

1. Big book of experiments for schoolchildren - M.: Rosman, 2009. - 264 p.

2. Wikipedia: https://ru.wikipedia.org/wiki/Archimedes_Law.

3. Perelman Ya.I. Entertaining physics. - book 1. - Ekaterinburg.: Thesis, 1994.

4. Perelman Ya.I. Entertaining physics. - book 2. - Ekaterinburg.: Thesis, 1994.

5. Peryshkin A.V. Physics: 7th grade: textbook for educational institutions / A.V. Peryshkin. - 16th ed., stereotype. - M.: Bustard, 2013. - 192 p.: ill.

Annex 1

Appendix 2

Appendix 3

Appendix 4

Lesson 48

Topic: "Archimedes' Law"

Objective of the lesson: derive a rule for calculating the Archimedean force
During the classes

1. 
   Checking homework

1. 
   State Pascal's law. (The pressure exerted on a liquid or gas is transmitted to any point equally in all directions)
2. 
   How to prove, based on Pascal's law, the existence of a buoyant force acting on a body immersed in a liquid? (The pressure on the upper surface of a body immersed in a liquid is less than the pressure of this liquid on its lower surface. The pressure force on the side surfaces is the same according to Pascal’s law. The pressure from below exceeds the pressure from above and tends to push the body to the surface.
3. 
   How to show experimentally that a buoyant force acts on a body in a liquid or gas? (Weigh a load or body first in air, then in liquid. The weight of the body in liquid or gas will be less due to the buoyant force.
4. 
   What is the direction of the buoyant force? (The force that pushes a body out of a liquid or gas is directed opposite to the force of gravity applied to this body)

F 1 = p 1 S 1 ; F 2 = p 2 S 2 ; since p 1 = ρ f ∙gh 1 ; p 2 = ρ f ∙gh 2 ; and S 1 = S 2 = S, where S is the area of ​​the base of the parallelepiped. Then F out = F 2 – F 1 = ρ t ∙gh 2 S – ρ t ∙gh 1 S = ρ t ∙gS (h 2 – h 1) = ρ t ∙gS h, where h is the height of the parallelepiped.

But S h= V, where V is the volume of the parallelepiped, and ρ f V = m f is the mass of the liquid in the parallelepiped. Therefore F out. = ρ f gV = gm f = P f. , that is, the buoyant force is equal to the weight of the liquid in the volume of the body immersed in it.)

1. 
   Learning new material.

Based on this experience we can conclude: the force pushing out a body completely immersed in a liquid is equal to the liquid in the volume of this body. The same can be said about bodies immersed in any gas. The force pushing a body out of a gas is also equal to the weight of the gas taken in the volume of the body.

The force that pushes a body out of a liquid or gas is called Archimedean force, in honor of the ancient Greek scientist Archimedes, who was the first to point out the existence of buoyant force and calculate its value. Archimedes' law states: if a body is immersed in a liquid (or gas), then it loses as much weight as the liquid (or gas) it displaces weighs.
Let's calculate it based on the above experiment: the Archimedean force is equal to the weight of the liquid in the volume of the body, i.e. F A = ​​P l = gm l. Let us express the mass of a liquid through its volume and density, i.e. m f = ρ f ∙V t. Consequently, the Archimedean force depends on the density of the liquid in which the body is immersed and on the volume of the body. Please note that the Archimedean force does not depend on the density of the substance of the body immersed in the liquid, since this value is not included in the resulting formula.

Let us now determine the weight of a body immersed in a liquid or gas. Since the two forces acting on the body are gravity and the Archimedean force are directed in opposite directions, the weight of the body in the liquid P 1 will be less than the weight of the body in vacuum P = gm (m is the mass of the body) by the Archimedean force F A = ​​gm w ( m l – mass of liquid or gas) displaced by the body, that is, P 1 = P - F A, or P 1 = gm - gm l.

Thus:

If Archimedean force is less than gravity (F A
- if the Archimedean force is equal to the force of gravity (F A = ​​gm), then the body will float;

If the Archimedean force is greater than the force of gravity (F A > gm), then the body will float.

1. 
   Consolidation of what has been learned

1. Ice floe area – 4 m2, thickness – 0.25 m. Will an ice floe be completely submerged in water if a person stands in the middle of it and is subject to a gravity force of 700 N? The density of ice is 900 kg/m 3, the density of water is 1000 kg/m 3.

F high = ρ f gV

V= Sh = 4x0.25 = 1.0m3; F = F t l + F t w = (0.25m ∙900kg/m 3 ∙1m 3)+ (0.25m ∙1000kg/m 3 ∙1m 3)= 475N. 700N >475 N. Answer: the ice floe will not sink.

2. A concrete slab with a volume of 2 m is immersed in water. How much force must be applied to keep it in the water? In the air?

1. 
   Homework

1. 
   § 49, questions to the paragraph
2. 
   Exercise 24 (1-3)

We already know that the Archimedes force is the resultant of the forces of fluid pressure on all parts of the body. In Fig. 22.5, and the forces acting on areas of the same area for a body of arbitrary shape are schematically depicted. With increasing depth, these forces increase - therefore, the resultant of all pressure forces is directed upward.

Rice. 22.5. Towards a proof of Archimedes' law for a body of arbitrary shape

Let us now mentally replace the body immersed in a liquid with the same liquid, which has “hardened”, maintaining its density (Fig. 22.5, b). The same Archimedes force will act on this “body” as on this body: after all, the surface of this “body” coincides with the surface of the selected volume of liquid, and the pressure forces on various parts of the surface remain the same.

The allocated volume of liquid, “floating” inside the same liquid, is in equilibrium. This means that the force of gravity F t and the Archimedes force F A acting on it balance each other, that is, they are equal in magnitude and directed oppositely (Fig. 22.5, c). For a body at rest, the force of gravity is equal to weight - this means that the Archimedes force is equal to the weight of the allocated volume of liquid. And this is the volume of the immersed part of the body: after all, it was this that we mentally replaced with liquid.

So, we have proven that an Archimedes force acts on a body of arbitrary shape, equal in magnitude to the weight of the liquid in the volume occupied by the body.

The above proof is an example of a thought experiment. This is a favorite reasoning technique for many scientists. Galileo was especially fond of thought experiments. But the conclusions obtained as a result of a thought experiment must be verified in a real experiment: after all, with the reasoning and assumptions that are inevitable in any thought experiment, a mistake can be made. Therefore, we will not limit ourselves to the given theoretical proof of Archimedes’ law and will test it using an equally beautiful experiment.

Let's put experience

Let's hang an empty bucket from a spring (it's called Archimedes' bucket), and from it a small stone of arbitrary shape (Fig. 22.6, a). Let's note the elongation of the spring and place a vessel under the stone into which water is poured to the level of the drain pipe (Fig. 22.6, b). When the stone is completely immersed, the water displaced by it will pour out through the pouring tube into the glass. We will notice that the elongation of the spring, due to the action of the buoyant force, has decreased.

Rice. 22.6. Experience shows that the Archimedes force is equal to the weight of water displaced by the body

Let us now pour the water displaced by the stone from the glass into Archimedes’ bucket - by doing this we will add to the weight of the stone precisely the weight of the water displaced by it. And we will see that the elongation of the spring has become the same as it was before the stone was immersed in water (Fig. 22.6, c). This means that Archimedes’ force is really equal in magnitude to the weight of the water displaced by the stone!

If we repeat the experiment, immersing the stone only partially in water, we will see that in this case, the Archimedes force is equal in magnitude to the weight of the water displaced by the stone.

In laboratory work No. 9 you will be able to test Archimedes' law experimentally.

1. How can you prove that the force pushing out a completely submerged body is equal to the weight of the liquid in the volume of this body?

Answer: as a result of Archimedes' experiment with a bucket.

2. Does a buoyant force act on a body completely immersed in gas?

Answer: yes.

3. Archimedean force- a force that pushes a body out of a liquid or gas.

4. Why is the force that pushes a body out of a liquid or gas called Archimedean force?

Answer: in honor of the ancient Greek scientist Archimedes, who first pointed out its existence and calculated its value.

5. What contributions did Archimedes (287-212 BC) make to science?

Answer: buoyant force. For the first time he pointed out the existence of buoyancy force and calculated its value.

6. By what formula is Archimedean force determined?

7. Fill out the diagram.

8. What is the magnitude and direction of the resulting force acting on a cork float with a volume of V = 0.5 cm 3, completely immersed in water to a certain depth? The density of cork and water, respectively, is p t = 200 kg/m 3, p b = 103 kg/m 3.

9. A brick with a mass mk = 1.8 kg, suspended on a rope, is immersed in water. How many times will the rope's gravity change?

2) If a brick is immersed in water (see figure on the right), then in addition to the force of gravity

10. What task was set for Archimedes by the Syracusan king Hiero (200 BC)?

Answer: determine whether the crown is solid or whether there are cavities and the craftsmen who made the crown deceived him.

11. How did Archimedes solve the golden crown problem?

12. In what essay is Archimedes’ law formulated?

Answer: about floating bodies.