Solve the system using Cramer's multiple regression method. Linear equations. Solving systems of linear equations. Cramer method

Cramer's method is based on the use of determinants in solving systems of linear equations. This significantly speeds up the solution process.

Cramer's method can be used to solve a system of as many linear equations as there are unknowns in each equation. If the determinant of the system is not equal to zero, then Cramer’s method can be used in the solution, but if it is equal to zero, then it cannot. In addition, Cramer's method can be used to solve systems of linear equations that have a unique solution.

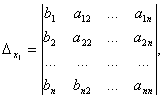
Definition. A determinant made up of coefficients for unknowns is called a determinant of the system and is denoted (delta).

Determinants

are obtained by replacing the coefficients of the corresponding unknowns with free terms:

;

.

Cramer's theorem. If the determinant of the system is nonzero, then the system of linear equations has one unique solution, and the unknown is equal to the ratio of the determinants. The denominator contains the determinant of the system, and the numerator contains the determinant obtained from the determinant of the system by replacing the coefficients of this unknown with free terms. This theorem holds for a system of linear equations of any order.

Example 1. Solve a system of linear equations:

According to Cramer's theorem we have:

So, the solution to system (2):

online calculator, Cramer's solving method.

Three cases when solving systems of linear equations

As is clear from Cramer's theorem, when solving a system of linear equations, three cases can occur:

First case: a system of linear equations has a unique solution

(the system is consistent and definite)

Second case: a system of linear equations has an infinite number of solutions

(the system is consistent and uncertain)

** ,

those. the coefficients of the unknowns and the free terms are proportional.

Third case: the system of linear equations has no solutions

(the system is inconsistent)

So the system m linear equations with n called variables non-joint, if she does not have a single solution, and joint, if it has at least one solution. A simultaneous system of equations that has only one solution is called certain, and more than one – uncertain.

Examples of solving systems of linear equations using the Cramer method

Let the system be given

.

Based on Cramer's theorem

………….
,

Where
-

system determinant. We obtain the remaining determinants by replacing the column with the coefficients of the corresponding variable (unknown) with free terms:

Example 2.

.

Therefore, the system is definite. To find its solution, we calculate the determinants

Using Cramer's formulas we find:

So, (1; 0; -1) is the only solution to the system.

To check solutions to systems of equations 3 X 3 and 4 X 4, you can use an online calculator using Cramer's solving method.

If in a system of linear equations there are no variables in one or more equations, then in the determinant the corresponding elements are equal to zero! This is the next example.

Example 3. Solve a system of linear equations using the Cramer method:

.

Solution. We find the determinant of the system:

Look carefully at the system of equations and at the determinant of the system and repeat the answer to the question in which cases one or more elements of the determinant are equal to zero. So, the determinant is not equal to zero, therefore the system is definite. To find its solution, we calculate the determinants for the unknowns

Using Cramer's formulas we find:

So, the solution to the system is (2; -1; 1).

To check solutions to systems of equations 3 X 3 and 4 X 4, you can use an online calculator using Cramer's solving method.

Top of page

We continue to solve systems using Cramer's method together

As already mentioned, if the determinant of the system is equal to zero, and the determinants of the unknowns are not equal to zero, the system is inconsistent, that is, it has no solutions. Let us illustrate with the following example.

Example 6. Solve a system of linear equations using the Cramer method:

Solution. We find the determinant of the system:

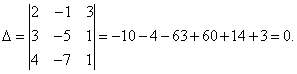
The determinant of the system is equal to zero, therefore, the system of linear equations is either inconsistent and definite, or inconsistent, that is, has no solutions. To clarify, we calculate determinants for unknowns

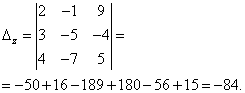
The determinants of the unknowns are not equal to zero, therefore, the system is inconsistent, that is, it has no solutions.

To check solutions to systems of equations 3 X 3 and 4 X 4, you can use an online calculator using Cramer's solving method.

In problems involving systems of linear equations, there are also those where, in addition to letters denoting variables, there are also other letters. These letters represent a number, most often real. In practice, such equations and systems of equations are led to by problems of searching for general properties of any phenomena or objects. That is, you have invented some new material or device, and to describe its properties, which are common regardless of the size or quantity of the specimen, you need to solve a system of linear equations, where instead of some coefficients for variables there are letters. You don't have to look far for examples.

The following example is for a similar problem, only the number of equations, variables, and letters denoting a certain real number increases.

Example 8. Solve a system of linear equations using the Cramer method:

Solution. We find the determinant of the system:

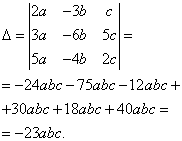
Finding determinants for unknowns

Cramer's method.

The Cramer method is used to solve systems of linear algebraic equations ( SLAU).

Formulas using the example of a system of two equations with two variables.
Given: Solve the system using Cramer's method

Regarding variables X And at.
Solution:
Let's find the determinant of the matrix, composed of the coefficients of the system Calculation of determinants. :

Let's apply Cramer's formulas and find the values ​​of the variables:
And .
Example 1:
Solve the system of equations:

regarding variables X And at.
Solution:


Let us replace the first column in this determinant with a column of coefficients from the right side of the system and find its value:

Let's do a similar thing, replacing the second column in the first determinant:

Applicable Cramer's formulas and find the values ​​of the variables:
And .
Answer:
Comment: This method can solve systems of higher dimensions.

Comment: If it turns out that , but cannot be divided by zero, then they say that the system does not have a unique solution. In this case, the system either has infinitely many solutions or has no solutions at all.

Example 2(infinite number of solutions):

Solve the system of equations:

regarding variables X And at.
Solution:
Let us find the determinant of the matrix, composed of the coefficients of the system:

Solving systems using the substitution method.

The first of the system's equations is an equality that is true for any values ​​of the variables (because 4 is always equal to 4). This means there is only one equation left. This is an equation for the relationship between variables.
We found that the solution to the system is any pair of values ​​of variables related to each other by the equality .
The general solution will be written as follows:
Particular solutions can be determined by choosing an arbitrary value of y and calculating x from this connection equality.

etc.
There are infinitely many such solutions.
Answer: common decision
Private solutions:

Example 3(no solutions, system is incompatible):

Solve the system of equations:

Solution:
Let us find the determinant of the matrix, composed of the coefficients of the system:

Cramer's formulas cannot be used. Let's solve this system using the substitution method

The second equation of the system is an equality that is not true for any values ​​of the variables (of course, since -15 is not equal to 2). If one of the equations of the system is not true for any values ​​of the variables, then the entire system has no solutions.
Answer: no solutions

With the same number of equations as the number of unknowns with the main determinant of the matrix, which is not equal to zero, the coefficients of the system (for such equations there is a solution and there is only one).

Cramer's theorem.

When the determinant of the matrix of a square system is non-zero, it means that the system is consistent and it has one solution and it can be found by Cramer's formulas:

where Δ - determinant of the system matrix,

Δ i is the determinant of the system matrix, in which instead of i The th column contains the column of right sides.

When the determinant of a system is zero, it means that the system can become cooperative or incompatible.

This method is usually used for small systems with extensive calculations and if it is necessary to determine one of the unknowns. The complexity of the method is that many determinants need to be calculated.

Description of the Cramer method.

There is a system of equations:

A system of 3 equations can be solved using the Cramer method, which was discussed above for a system of 2 equations.

We compose a determinant from the coefficients of the unknowns:

It will be system determinant. When D≠0, which means the system is consistent. Now let's create 3 additional determinants:

,,

We solve the system by Cramer's formulas:

Examples of solving systems of equations using Cramer's method.

Example 1.

Given system:

Let's solve it using Cramer's method.

First you need to calculate the determinant of the system matrix:

Because Δ≠0, which means that from Cramer’s theorem the system is consistent and it has one solution. We calculate additional determinants. The determinant Δ 1 is obtained from the determinant Δ by replacing its first column with a column of free coefficients. We get:

In the same way, we obtain the determinant of Δ 2 from the determinant of the system matrix by replacing the second column with a column of free coefficients:

Cramer's method or the so-called Cramer's rule is a method of searching for unknown quantities from systems of equations. It can be used only if the number of sought values ​​is equivalent to the number of algebraic equations in the system, that is, the main matrix formed from the system must be square and not contain zero rows, and also if its determinant must not be zero.

Theorem 1

Cramer's theorem If the main determinant $D$ of the main matrix, compiled on the basis of the coefficients of the equations, is not equal to zero, then the system of equations is consistent, and it has a unique solution. The solution to such a system is calculated through the so-called Cramer formulas for solving systems of linear equations: $x_i = \frac(D_i)(D)$

What is the Cramer method?

The essence of Cramer's method is as follows:

1. To find a solution to the system using Cramer's method, first of all we calculate the main determinant of the matrix $D$. When the calculated determinant of the main matrix, when calculated by Cramer's method, turns out to be equal to zero, then the system does not have a single solution or has an infinite number of solutions. In this case, to find a general or some basic answer for the system, it is recommended to use the Gaussian method.
2. Then you need to replace the outermost column of the main matrix with a column of free terms and calculate the determinant $D_1$.
3. Repeat the same for all columns, obtaining determinants from $D_1$ to $D_n$, where $n$ is the number of the rightmost column.
4. After all determinants $D_1$...$D_n$ have been found, the unknown variables can be calculated using the formula $x_i = \frac(D_i)(D)$.

Techniques for calculating the determinant of a matrix

To calculate the determinant of a matrix with a dimension greater than 2 by 2, you can use several methods:

• The rule of triangles, or Sarrus's rule, reminiscent of the same rule. The essence of the triangle method is that when calculating the determinant, the products of all numbers connected in the figure by the red line on the right are written with a plus sign, and all numbers connected in a similar way in the figure on the left are written with a minus sign. Both rules are suitable for matrices of size 3 x 3. In the case of the Sarrus rule, the matrix itself is first rewritten, and next to it its first and second columns are rewritten again. Diagonals are drawn through the matrix and these additional columns; matrix members lying on the main diagonal or parallel to it are written with a plus sign, and elements lying on or parallel to the secondary diagonal are written with a minus sign.

Figure 1. Triangle rule for calculating the determinant for Cramer's method

• Using a method known as the Gaussian method, this method is also sometimes called reducing the order of the determinant. In this case, the matrix is ​​transformed and reduced to triangular form, and then all the numbers on the main diagonal are multiplied. It should be remembered that when searching for a determinant in this way, you cannot multiply or divide rows or columns by numbers without taking them out as a multiplier or divisor. In the case of searching for a determinant, it is only possible to subtract and add rows and columns to each other, having previously multiplied the subtracted row by a non-zero factor. Also, whenever you rearrange the rows or columns of the matrix, you should remember the need to change the final sign of the matrix.
• When solving a SLAE with 4 unknowns using the Cramer method, it is best to use the Gauss method to search and find determinants or determine the determinant by searching for minors.

Solving systems of equations using Cramer's method

Let's apply Cramer's method for a system of 2 equations and two required quantities:

$\begin(cases) a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end(cases)$

Let's display it in expanded form for convenience:

$A = \begin(array)(cc|c) a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end(array)$

Let's find the determinant of the main matrix, also called the main determinant of the system:

$D = \begin(array)(|cc|) a_1 & a_2 \\ a_3 & a_4 \\ \end(array) = a_1 \cdot a_4 – a_3 \cdot a_2$

If the main determinant is not equal to zero, then to solve the slough using Cramer’s method it is necessary to calculate a couple more determinants from two matrices with the columns of the main matrix replaced by a row of free terms:

$D_1 = \begin(array)(|cc|) b_1 & a_2 \\ b_2 & a_4 \\ \end(array) = b_1 \cdot a_4 – b_2 \cdot a_4$

$D_2 = \begin(array)(|cc|) a_1 & b_1 \\ a_3 & b_2 \\ \end(array) = a_1 \cdot b_2 – a_3 \cdot b_1$

Now let's find the unknowns $x_1$ and $x_2$:

$x_1 = \frac (D_1)(D)$

$x_2 = \frac (D_2)(D)$

Example 1

Cramer's method for solving SLAEs with a main matrix of 3rd order (3 x 3) and three required ones.

Solve the system of equations:

$\begin(cases) 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 - x_3 = 10 \\ \end(cases)$

Let's calculate the main determinant of the matrix using the rule stated above under point number 1:

$D = \begin(array)(|ccc|) 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end(array) = 3 \cdot 4 \cdot ( -1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) - (- 1) \cdot 2 \cdot 3 = - 12 – 8 -12 -32 – 6 + 6 = - 64$

And now three other determinants:

$D_1 = \begin(array)(|ccc|) 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end(array) = 21 \cdot 4 \cdot 1 + (- 2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) - (-1) \cdot 2 \ cdot 21 = - 84 – 40 – 36 – 160 – 18 + 42 = - $296

$D_2 = \begin(array)(|ccc|) 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end(array) = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = - 27 + 120 + 84 – 72 + 63 – 60 = $108

$D_3 = \begin(array)(|ccc|) 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end(array) = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 - (-2) \cdot 3 \cdot 10 - (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = - $60

Let's find the required quantities:

$x_1 = \frac(D_1) (D) = \frac(- 296)(-64) = 4 \frac(5)(8)$

$x_2 = \frac(D_1) (D) = \frac(108) (-64) = - 1 \frac (11) (16)$

$x_3 = \frac(D_1) (D) = \frac(-60) (-64) = \frac (15) (16)$

Consider a system of 3 equations with three unknowns

Using 3rd order determinants, the solution to such a system can be written in the same form as for a system of two equations, i.e.

(2.4)

if 0. Here

It's there Cramer's rule solving a system of three linear equations in three unknowns.

Example 2.3. Solve a system of linear equations using Cramer's rule:

Solution . Finding the determinant of the main matrix of the system

Since 0, then to find a solution to the system we can apply Cramer’s rule, but first we calculate three more determinants:

Examination:

Therefore, the solution was found correctly. 

Cramer's rules obtained for linear systems of 2nd and 3rd order suggest that the same rules can be formulated for linear systems of any order. Really happens

Cramer's theorem. Quadratic system of linear equations with a nonzero determinant of the main matrix of the system (0) has one and only one solution and this solution is calculated using the formulas

(2.5)

Where  – determinant of the main matrix,  i – matrix determinant, obtained from the main one, replacingith column column of free terms.

Note that if =0, then Cramer’s rule does not apply. This means that the system either has no solutions at all or has infinitely many solutions.

Having formulated Cramer's theorem, the question naturally arises of calculating determinants of higher orders.

2.4. Determinants of nth order

Additional minor M ij element a ij is a determinant obtained from a given by deleting i th line and j th column. Algebraic complement A ij element a ij the minor of this element taken with the sign (–1) is called i + j, i.e. A ij = (–1) i + j M ij .

For example, let's find the minors and algebraic complements of the elements a 23 and a 31 qualifiers

We get



Using the concept of algebraic complement we can formulate determinant expansion theoremn-th order by row or column.

Theorem 2.1. Matrix determinantAis equal to the sum of the products of all elements of a certain row (or column) by their algebraic complements:

(2.6)

This theorem underlies one of the main methods for calculating determinants, the so-called. order reduction method. As a result of the expansion of the determinant n th order over any row or column, we get n determinants ( n–1)th order. To have fewer such determinants, it is advisable to select the row or column that has the most zeros. In practice, the expansion formula for the determinant is usually written as:

those. algebraic additions are written explicitly in terms of minors.

Examples 2.4. Calculate the determinants by first sorting them into some row or column. Typically, in such cases, select the column or row that has the most zeros. The selected row or column will be indicated by an arrow.



2.5. Basic properties of determinants

Expanding the determinant over any row or column, we get n determinants ( n–1)th order. Then each of these determinants ( n–1)th order can also be decomposed into a sum of determinants ( n–2)th order. Continuing this process, one can reach the 1st order determinants, i.e. to the elements of the matrix whose determinant is calculated. So, to calculate 2nd order determinants, you will have to calculate the sum of two terms, for 3rd order determinants - the sum of 6 terms, for 4th order determinants - 24 terms. The number of terms will increase sharply as the order of the determinant increases. This means that calculating determinants of very high orders becomes a rather labor-intensive task, beyond the capabilities of even a computer. However, determinants can be calculated in another way, using the properties of determinants.

Property 1 . The determinant will not change if the rows and columns in it are swapped, i.e. when transposing a matrix:

.

This property indicates the equality of the rows and columns of the determinant. In other words, any statement about the columns of a determinant is also true for its rows and vice versa.

Property 2 . The determinant changes sign when two rows (columns) are interchanged.

Consequence . If the determinant has two identical rows (columns), then it is equal to zero.

Property 3 . The common factor of all elements in any row (column) can be taken out of the determinant sign.

For example,

Consequence . If all elements of a certain row (column) of a determinant are equal to zero, then the determinant itself is equal to zero.

Property 4 . The determinant will not change if the elements of one row (column) are added to the elements of another row (column), multiplied by any number.

For example,

Property 5 . The determinant of the product of matrices is equal to the product of the determinants of matrices: