Temukan induksi medan magnet yang diciptakan oleh garis lurus

Ketika arus searah melewati rangkaian tertutup yang terletak dalam ruang hampa, untuk suatu titik yang terletak jauh dari rangkaian, induksi magnet akan berbentuk:

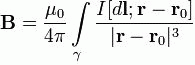
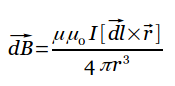
Jika jarum magnet didekatkan pada penghantar lurus yang berarus, maka jarum tersebut akan cenderung tegak lurus terhadap bidang yang melalui sumbu penghantar dan pusat putaran jarum (Gbr. 67).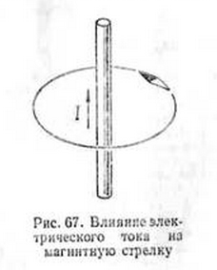

Hal ini menunjukkan bahwa jarum terkena gaya khusus yang disebut gaya magnet. Dengan kata lain, jika seorang kondektur lewat listrik, kemudian muncul medan magnet di sekitar konduktor.

Medan magnet dapat dianggap sebagai keadaan ruang khusus yang mengelilingi konduktor pembawa arus. Saat menghitung medan magnet, besaran yang disebut ketegangan Medan gaya (dilambangkan H). Induksi magnet B dan kuat medan magnet H dihubungkan dengan hubungan:

Satuan ukuran kuat medan magnet adalah ampere per meter (A/m).

Kekuatan medan magnet dalam media homogen, serta induksi magnet, bergantung pada besarnya arus, jumlah dan bentuk konduktor yang dilalui arus. Namun tidak seperti induksi magnet, kekuatan medan magnet tidak memperhitungkan pengaruh sifat magnet medium.

34. Perhitungan menggunakan hukum BS medan magnet pada sumbu kumparan melingkar berarus Analogi medan listrik diapol.

Kekuatan medan magnet adalah rasionya kekuatan mekanis, yang bekerja pada kutub positif magnet uji, dengan nilai massa magnet atau gaya mekanis yang bekerja pada kutub positif magnet uji dengan satuan massa pada suatu titik tertentu di medan. Intensitas dinyatakan dengan vektor H, memiliki arah vektor gaya mekanik F: .Elemen saat ini- besaran vektor yang sama dengan produk arus konduksi sepanjang konduktor linier dan segmen yang sangat kecil dari konduktor ini. . Catatan. Elemen saat ini memiliki arah yang bertepatan dengan arah segmen ini. Hukum Biot-Savart-Laplace - hukum fisika untuk menentukan vektor induksi medan magnet yang ditimbulkan oleh arus listrik searah.

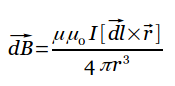
Konduktor melingkar yang membawa arus.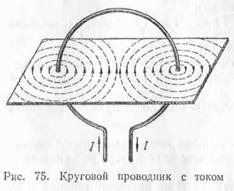

Mari kita ambil sebuah konduktor yang ditekuk membentuk lingkaran dalam bentuk kumparan dan mengalirkan arus melaluinya (Gbr. 75). Dari gambar tersebut terlihat bahwa garis-garis magnet melingkari penghantar berarus dan berbentuk lingkaran. Garis-garis magnet di satu sisi memasuki bidang konduktor melingkar, di sisi lain keluar. Arah medan arus melingkar dapat ditentukan dengan menggunakan "aturan gimlet". Gimlet harus diposisikan sepanjang sumbu arus melingkar yang tegak lurus terhadap pesawatnya. Jika sekarang Anda memutar pegangan gimlet searah dengan arus pada rangkaian, maka gerakan translasi gimlet akan menunjukkan arah medan magnet. Kuat medan magnet pada bagian tengah kumparan yang berarus ditentukan dengan rumus:

35. Fluks vektor induksi magnet (fluks magnet) dan makna geometrinya Teorema OG untuk medan magnet.

Fluks vektor induksi magnet (fluks magnet) yang melalui luas dS disebut skalar kuantitas fisik, setara dimana Bn=B cos a adalah proyeksi vektor B ke arah garis normal situs dS (a adalah sudut antara vektor n dan B), dS=dSn adalah vektor yang modulusnya sama dengan dS, dan arahnya bertepatan dengan arah n normal ke lokasi. Fluks vektor B dapat positif atau negatif tergantung pada tanda cos a (ditentukan oleh pilihan arah positif dari normal n). Aliran vektor B berhubungan dengan rangkaian yang dilalui arus. Dalam hal ini, arah positif dari normal ke kontur telah kita tentukan: ini dikaitkan dengan arus dengan aturan sekrup kanan. Jadi, fluks magnet yang diciptakan oleh rangkaian melalui permukaan yang dibatasi oleh dirinya sendiri selalu positif. Fluks vektor induksi magnet ФB melalui permukaan sembarang S Untuk lapangan seragam dan permukaan datar terletak tegak lurus terhadap vektor B, Bn=B=konstan dan Dari rumus ini ditentukan satuan fluks magnet Weber (Wb): 1 Wb - fluks magnet yang melewati permukaan datar dengan luas 1 m2 terletak tegak lurus terhadap medan magnet seragam, yang induksinya sama dengan 1 T (1 Wb=1 T×m2). Teorema Gauss untuk medan B: fluks vektor induksi magnet yang melalui setiap permukaan tertutup adalah nol: Teorema ini mencerminkan fakta bahwa tidak ada muatan magnetik, akibatnya garis-garis induksi magnet tidak memiliki awal atau akhir dan tertutup. Jadi, untuk aliran vektor B dan E melalui permukaan tertutup pada pusaran dan medan potensial, hasilnya berbeda. Sebagai contoh, mari kita hitung aliran vektor B melalui solenoida. Induksi magnet medan seragam di dalam solenoida dengan inti dengan permeabilitas magnet m, menurut, sama dengan Fluks magnet yang melalui satu putaran solenoida dengan luas S sama dengan dan total fluks magnet yang terikat pada semua putaran solenoida dan disebut hubungan fluks, . Momen magnet pada suatu rangkaian berarus. Rangkaian dengan arus dalam medan magnet. Pengalaman menunjukkan bahwa arus listrik saling berinteraksi, misalnya arus I tarik menarik dan arus tolak menolak. Interaksi arus terjadi melalui medan yang disebut magnet. Akibatnya, muatan (arus) yang bergerak mengubah sifat ruang di sekitarnya - menciptakan medan magnet di dalamnya. Bidang ini memanifestasikan dirinya dalam kenyataan bahwa gaya-gaya bekerja pada muatan (arus) yang bergerak di dalamnya. Mirip dengan penelitian Medan listrik Kami menggunakan muatan uji; untuk mempelajari medan magnet, kami akan menggunakan arus uji yang bersirkulasi dalam rangkaian tertutup datar dengan dimensi yang sangat kecil. Kita akan menyebut rangkaian seperti itu sebagai rangkaian percobaan. Orientasinya dalam ruang ditandai dengan arah normal n(vektor) ke kontur, dipulihkan sesuai dengan aturan gimlet kanan: kita memutar pegangan gimlet kanan ke arah arus di sirkuit, lalu arah gerak translasinya akan memberikan arah n(vektor) normal (lihat Gambar 1). Dengan menempatkan rangkaian uji dalam medan magnet, kita menemukan bahwa medan tersebut cenderung memutar rangkaian (normal) ke arah tertentu. 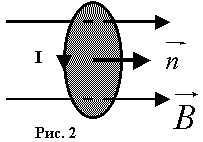Torsi yang bekerja pada rangkaian bergantung pada sifat medan magnet pada suatu titik tertentu dan sifat rangkaian. Ternyata nilai torsi maksimum sebanding dengan IS yaitu. Mmax ~ IS, dimana I adalah arus pada rangkaian, S adalah luas rangkaian yang berarus (Gbr. 1). Besaran vektor (1) disebut momen magnet rangkaian, yang dalam SI diukur dalam A×m2. Sirkuit uji dengan pm berbeda yang ditempatkan pada titik tertentu dalam medan magnet akan dikenakan torsi maksimum M yang berbeda, namun rasio Mmax/pm akan sama untuk semua sirkuit; ini akan menjadi karakteristik gaya medan magnet, yaitu disebut induksi magnet B = Mmax /pm Induksi magnet adalah suatu vektor yang arahnya berimpit dengan arah garis normal suatu rangkaian berarus, yang terbentuk bebas dalam medan magnet luar (lihat Gambar 2). dapat direpresentasikan menggunakan garis gaya, (lihat Gambar 2), serta medan vektor sehingga B analog dengan E. Induksi magnetik dalam SI diukur dalam teslas: 1 T = 1 Nm/1 A×m2. Tesla sama dengan induksi magnet medan seragam, dimana torsi maksimum sebesar 1 Nm bekerja pada rangkaian datar dengan arus yang mempunyai momen magnet 1 A m2. Suatu rangkaian pembawa arus yang ditempatkan dalam medan magnet dengan induksi dikenai torsi yang besarnya M =. Pekerjaan menggerakkan konduktor dan rangkaian pembawa arus dalam medan magnet. Usaha yang dilakukan oleh suatu penghantar terhadap arus ketika bergerak secara numerik sama dengan hasil kali arus dan fluks magnet yang dilintasi oleh penghantar tersebut. Mari kita perhatikan rangkaian pembawa arus yang dibentuk oleh kabel tetap dan jumper bergerak dengan panjang l yang meluncur di sepanjang kabel tersebut (Gbr. 2.17). Rangkaian ini terletak pada medan magnet luar seragam B, tegak lurus terhadap bidang rangkaian. Dengan arah arus I yang ditunjukkan pada gambar, vektor B searah dengan n. 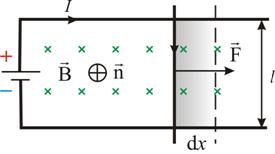Elemen arus I (kawat bergerak) dengan panjang l dikenai gaya Ampere yang arahnya ke kanan: Biarkan penghantar l bergerak sejajar dengan dirinya sendiri sejauh tertentu. Dalam hal ini, usaha yang dilakukan adalah: Jadi: Rumusnya tetap berlaku jika sebuah konduktor berbentuk apa pun bergerak pada sudut mana pun terhadap garis vektor induksi magnet. Usaha yang dilakukan ketika suatu rangkaian tertutup yang berarus bergerak dalam medan magnet sama dengan hasil kali besar arus dan perubahan fluks magnet yang berhubungan dengan rangkaian tersebut. Perhatikan rangkaian persegi panjang dengan arus 1-2-3-4-1 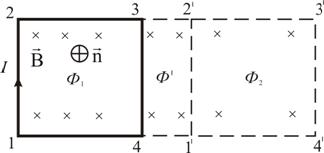(Gbr. 2.18). Medan magnet diarahkan menjauhi kita tegak lurus terhadap bidang kontur. Oleh karena itu, fluks magnet yang menembus rangkaian diarahkan sepanjang n normal ke rangkaian. Beras. 2.18 Mari kita pindahkan rangkaian ini sejajar dengan dirinya ke posisi baru 1"-2"-3"-4"-1". Medan magnet dalam kasus umum bisa tidak seragam dan rangkaian baru akan ditembus oleh fluks magnet .Area 4-3-2"-1"-4 yang terletak di antara sirkuit lama dan sirkuit baru ditembus oleh aliran. Pekerjaan penuh dengan menggerakkan rangkaian dalam medan magnet sama dengan jumlah aljabar usaha yang dilakukan ketika menggerakkan keempat sisi rangkaian: , dimana, sama dengan nol, karena sisi-sisi ini tidak melewati fluks magnet ketika bergerak (garis besar area nol). Kawat 1–2 memotong aliran, tetapi bergerak melawan gaya medan magnet. Kemudian pekerjaan umum dengan gerakan kontur: atau di sini adalah perubahan fluks magnet yang digabungkan ke rangkaian.

B - induksi magnet
μ0 - konstanta magnet
Saya - kekuatan saat ini
r - jarak ke konduktor

Induksi medan magnet pada pusat arus melingkar (putaran)

B - induksi magnet
μ - permeabilitas magnetik relatif
μ0 - konstanta magnet
Saya - kekuatan saat ini
R - radius

Kekuatan medan magnet disebut besaran vektor yang mencirikan medan magnet dan didefinisikan sebagai berikut:

Kekuatan medan magnet: kawat lurus tak terbatas

Saya - kekuatan saat ini
r - jarak ke konduktor

Kekuatan medan magnet di pusat kumparan

H - kekuatan medan magnet

Saya - kekuatan saat ini
R - radius

Hukum Biot-Savart-Laplace.

Hukum Biot-Savart-Laplace- Medan magnet dari setiap arus dapat dihitung sebagai jumlah vektor dari medan yang diciptakan oleh masing-masing bagian arus.

Perumusan

Biarkan arus searah mengalir sepanjang kontur γ yang terletak dalam ruang hampa - titik di mana medan dicari, maka induksi medan magnet pada titik ini dinyatakan dengan integral (dalam sistem SI)

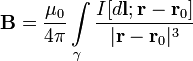
Arahnya tegak lurus dan, yaitu tegak lurus terhadap bidang tempatnya berada, dan bertepatan dengan garis singgung garis induksi magnet. Arah ini dapat dicari dengan aturan mencari garis induksi magnet (aturan sekrup sebelah kanan): arah putaran kepala sekrup memberikan arah jika gerakan translasi gimlet sesuai dengan arah arus dalam elemen. . Besarnya vektor ditentukan oleh ekspresi (dalam sistem SI)

Potensi vektor diberikan oleh integral (dalam SI)

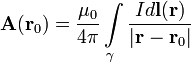
Konsep kinetik molekuler tentang struktur materi dalam berbagai keadaan agregasi.

Sebuah metode statistik untuk menggambarkan keadaan dan perilaku sistem multipartikel.

Distribusi molekul gas ideal menurut keadaan:

Benda-benda di sekitar kita (padat, cair, gas) dianggap oleh indera kita sebagai benda padat. Namun benda tersebut tidak padat, melainkan terdiri dari partikel-partikel kecil yang tidak terlihat dengan mata telanjang, letaknya tidak berdekatan satu sama lain, melainkan pada jarak tertentu. Partikel materi terkecil ini disebut molekul (kecil dari kata Latin untuk “massa”).

Democritus (abad ke-5 SM) menyebut partikel terkecil penyusun seluruh benda di dunia sebagai atom (tidak dapat dibagi-bagi). Menurut Democritus, atom mempunyai ukuran yang berbeda, berat, bentuk, dll.

1) Semua zat terdiri dari partikel kecil – molekul. Molekul adalah partikel terkecil suatu zat yang dapat menampung seluruhnya Sifat kimia. Semua molekul yang terbentuk zat ini, sama persis. Molekul terdiri dari atom. Atom adalah partikel terkecil unsur kimia(105 buah - 94 alami dan 11 buatan).

2) Gaya tarik-menarik dan tolak-menolak bekerja secara simultan antar molekul-molekul suatu benda.

3) Molekul-molekul pembentuk benda berada dalam keadaan gerak acak terus menerus (osilasi).

Semakin tinggi suhu tubuh, semakin cepat molekul bergerak. Suhu adalah ukuran rata-rata energi kinetik molekul tubuh. Kecepatan pergerakan molekul-molekul suatu benda, yang menentukan energi kinetik, menentukan keadaan termal suatu benda dan jumlah energi internalnya. Pergerakan molekul yang kacau disebut termal.

Pemisahan molekul menjadi atom disebut disosiasi. Disosiasi terjadi di bawah pengaruh 1) suhu tinggi, 2) reaksi kimia, 3) iradiasi.

Termodinamika didasarkan pada dua metode mempelajari partikel: termodinamika dan statis.

Perilaku sejumlah besar molekul yang membentuk makrobodi dipelajari dengan metode statistik, yang didasarkan pada fakta bahwa sifat-sifat makrobodi ditentukan oleh sifat-sifat molekul, karakteristik pergerakannya (kecepatan, energi, momentum). , dll.) dan interaksi. Misalnya, suhu dapat dinyatakan dalam energi kinetik rata-rata gerak molekul. Metode statistik memberikan gambaran tentang mekanisme proses termal, menganggapnya seolah-olah dari dalam benda makro; metode ini secara signifikan melengkapi metode termodinamika. Hukum dasar termodinamika juga mempunyai arti statistik.

Dalam gas yang berada dalam keadaan setimbang, distribusi kecepatan molekul tertentu yang stasioner (tidak berubah seiring waktu) akan terbentuk, yang mematuhi hukum statistik yang terdefinisi dengan baik. Hukum ini secara teoritis diturunkan oleh Maxwell.

Ketika menurunkan hukum ini, Maxwell berasumsi bahwa gas terdiri dari sangat banyak jumlah besar N molekul identik dalam keadaan gerak termal acak pada suhu yang sama. Diasumsikan juga bahwa ladang luar tidak bereaksi terhadap gas.

Hukum Maxwell dijelaskan oleh fungsi tertentu f(v), yang disebut fungsi distribusi kecepatan molekul. Ada tiga bentuk penulisan distribusi Maxwell.

Hukum kedua Newton untuk benda titik yang bergerak melingkar.

Mempertimbangkan ( ) dan () torsi tubuh

Ungkapan ini analog dengan hukum kedua Newton untuk gerak rotasi, yang kemudian diikuti dengan percepatan sudut padat ketika berputar pada sumbu tetap, itu berbanding lurus dengan torsi dan berbanding terbalik dengan momen inersia relatif terhadap sumbu ini. Dari ungkapan ini dapat disimpulkan bahwa momen inersia U adalah ukuran inersianya dalam gerak rotasi mengelilingi sumbu tetap. Dalam kasus gerak translasi, ukuran inersia, seperti diketahui, adalah massa benda.

Berikan contoh dan tunjukkan gaya-gaya yang menyebabkan percepatan sentripetal.

Rotasi planet, dimana gravitasi berperan sebagai gaya sentripetal. Tidak ada gaya sentrifugal di sana. Gaya sentrifugal merupakan gaya fiktif yang diperkenalkan untuk memudahkan perhitungan, sehingga lebih mudah untuk melakukan perhitungan dalam sistem non-inersia.

Fluks medan magnet.

Fluks magnet (fluks garis induksi magnet) melalui kontur secara numerik sama dengan hasil kali besar vektor induksi magnet dengan luas yang dibatasi oleh kontur dan kosinus sudut antara arah vektor induksi magnet dan garis normal permukaan yang dibatasi oleh kontur tersebut.

Rumus kerja gaya Ampere pada gerak penghantar lurus dengan DC dalam medan magnet seragam.

Jadi, usaha yang dilakukan oleh gaya Ampere dapat dinyatakan dalam arus pada konduktor yang dipindahkan dan perubahan fluks magnet melalui rangkaian di mana konduktor tersebut dihubungkan:

Induktansi lingkaran.

Induktansi- fisik kuantitas secara numerik sama ggl yang diinduksi sendiri, yang terjadi pada rangkaian ketika arus berubah sebesar 1 Ampere dalam 1 detik.
Induktansi juga dapat dihitung menggunakan rumus:

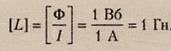di mana adalah fluks magnet yang melalui rangkaian, I adalah kuat arus dalam rangkaian.

Satuan SI untuk induktansi:

Energi medan magnet.

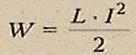Medan magnet mempunyai energi. Sama seperti kapasitor bermuatan yang mempunyai cadangan energi listrik, pada kumparan yang melalui lilitannya arus mengalir, terdapat cadangan energi magnet.

Penerapan interferensi cahaya dari sumber cahaya konvensional.

Interferensi cahaya pada film tipis. Kondisi interferensi maksimum dan minimum cahaya pada film dalam cahaya yang dipantulkan dan ditransmisikan.

Pinggir interferensi dengan ketebalan yang sama dan pinggiran interferensi dengan kemiringan yang sama.

1)Fenomena interferensi diamati pada lapisan tipis cairan yang tidak dapat bercampur (minyak tanah atau minyak pada permukaan air), dalam gelembung sabun, bensin, pada sayap kupu-kupu, dalam warna yang ternoda, dll.

2) 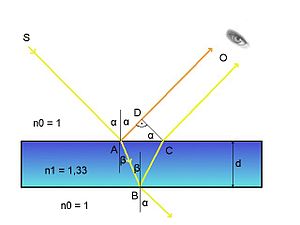interferensi terjadi ketika seberkas cahaya asli terbelah menjadi dua berkas saat melewatinya film pendek, misalnya, film yang diaplikasikan pada permukaan lensa lensa berlapis. Sinar cahaya yang melewati lapisan film tebal akan dipantulkan dua kali - dari permukaan dalam dan luarnya. Sinar pantul akan mempunyai beda fasa yang konstan sama dengan dua kali ketebalan film, sehingga menyebabkan sinar menjadi koheren dan berinterferensi. Padamnya sinar secara sempurna akan terjadi pada , dimana adalah panjang gelombang. Jika nm, maka ketebalan filmnya adalah 550:4 = 137,5 nm.

Sinar dari bagian spektrum yang berdekatan di kedua sisi nm tidak berinterferensi sepenuhnya dan hanya dilemahkan, menyebabkan film memperoleh warna. Dalam pendekatan optik geometris, ketika masuk akal untuk berbicara tentang perbedaan optik pada jalur sinar, untuk dua sinar

Kondisi maksimal;

Kondisi minimal

dimana k=0,1,2… dan merupakan panjang jalur optik masing-masing berkas pertama dan kedua.

3)Strip dengan kemiringan yang sama

Sangat penting kasus spesial interferensi cahaya yang dipantulkan oleh dua permukaan pelat bidang sejajar ketika titik pengamatan P berada di tak terhingga, yaitu. observasi dilakukan baik dengan mata yang ditampung hingga tak terhingga, atau pada layar yang terletak pada bidang fokus lensa pengumpul (Gbr. 8.8).

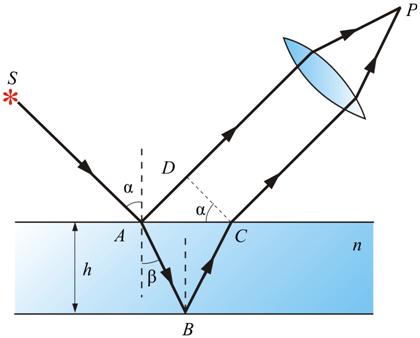
Dalam hal ini, kedua sinar yang datang dari S ke P dihasilkan oleh satu sinar datang dan, setelah dipantulkan dari permukaan depan dan belakang pelat, sejajar satu sama lain. Perbedaan jalur optik antara keduanya di titik P sama dengan pada garis DC:

Di sini n adalah indeks bias bahan pelat. Diasumsikan ada udara di atas pelat, mis. . Karena 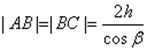, (h adalah tebal pelat, dan merupakan sudut datang dan bias pada permukaan atas; ), maka untuk selisih lintasan diperoleh

12.7 Perhitungan induksi medan magnet.

Hukum Biot-Savarre-Laplace dan prinsip superposisi memungkinkan penghitungan induksi medan magnet \(~\vec B\) yang diciptakan oleh sistem arbitrer arus listrik, pada titik sembarang dalam ruang. Untuk melakukan ini, semua arus perlu dibagi menjadi beberapa bagian yang sangat kecil \(~(I \Delta \vec l)_k\), tuliskan ekspresi vektor untuk induksi medan \(~(\Delta \vec B)_k\ ) dibuat oleh elemen-elemen ini ( menggunakan hukum Biot-Savarre-Laplace) dan menjumlahkan ekspresi yang dihasilkan (yang memungkinkan prinsip superposisi) untuk semua bagian arus

\(~\vec B = \sum_(k) ((\Delta \vec B)_k)\) . (1)

Mari kita lihat kembali bagian konduktor yang membawa arus (Gbr. 29). Ekspresi untuk elemen saat ini \(~I \Delta \vec l\) juga ditulis dalam bentuk \(~I \Delta \vec l = \vec j S \Delta l = \vec j \Delta V\) . Dalam kasus ketika arus listrik tidak linier, tetapi terdistribusi secara spasial (yaitu, arus tidak hanya mengalir sepanjang kabel tipis), ekspresi untuk elemen arus \(~I \Delta \vec l\) harus diganti dengan persamaan \(~\vec j \Delta V\) dan penjumlahannya harus dilakukan pada semua elemen volume yang berarus listrik mengalir.

Tentu saja, penjumlahan seperti itu seringkali merupakan masalah matematika yang rumit (bagaimanapun juga, Anda dapat menggunakan komputer untuk melakukannya), tetapi dari sudut pandang fisik, metode yang disajikan memberikan hasil yang lebih baik. solusi lengkap tugas.

Mari kita perhatikan beberapa contoh penghitungan induksi medan magnet menggunakan metode yang diuraikan di atas.

12.7.1 Medan magnet arus melingkar.

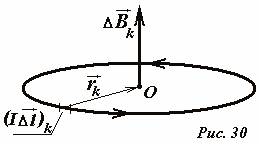
Biarkan arus listrik konstan SAYA mengalir sepanjang kontur lingkaran datar berjari-jari R. Mari kita cari induksi medan di pusat cincin di titik tersebut HAI(Gbr. 30). Mari kita secara mental membagi cincin menjadi beberapa bagian kecil yang dapat dianggap bujursangkar, dan menerapkan hukum Biot-Savarre-Laplace untuk menentukan induksi medan yang diciptakan oleh elemen ini di tengah cincin. Dalam hal ini, vektor elemen saat ini \(~(I \Delta \vec l)_k\) dan vektor \(~\vec r_k\) yang menghubungkan elemen ini dengan titik pengamatan (pusat cincin) adalah tegak lurus, oleh karena itu \(\dosa \alfa = 1\) . Vektor induksi medan yang diciptakan oleh bagian cincin yang dipilih diarahkan sepanjang sumbu cincin, dan modulusnya sama dengan

\(~\Delta B_k = \frac(\mu_0)(4 \pi) \frac((I \Delta l)_k)(R^2)\) . (1)

Untuk elemen cincin lainnya, situasinya sangat mirip - vektor induksi juga diarahkan sepanjang sumbu cincin, dan modulusnya ditentukan oleh rumus (1). Oleh karena itu, penjumlahan vektor-vektor ini dilakukan secara mendasar dan direduksi menjadi penjumlahan panjang bagian-bagian cincin.

\(~B = \sum_k \Delta B_k = \sum_k \frac(\mu_0)(4 \pi) \frac((I \Delta l)_k)(R^2) = \frac(\mu_0)(4 \ pi) \frac(I)(R^2) \sum_k (\Delta l)_k = \frac(\mu_0)(4 \pi) \frac(I)(R^2) 2 \pi R = \frac( \mu_0 I)(2 Kanan)\) . (2)

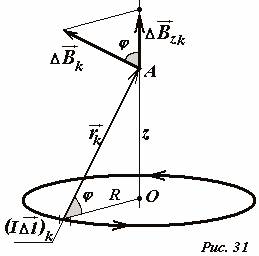
Mari kita rumitkan masalahnya - temukan induksi medan pada titik tersebut A, terletak pada sumbu cincin di kejauhan z dari pusatnya (Gbr. 31). Seperti sebelumnya, kita memilih bagian kecil dari cincin \(~(I \Delta \vec l)_k\) dan membuat vektor induksi dari bidang \(~(\Delta \vec B)_k\) yang dibuat oleh elemen ini pada titik yang dimaksud. Vektor ini tegak lurus terhadap vektor \(~\vec r\) yang menghubungkan area yang dipilih dengan titik pengamatan. Vektor \(~(I \Delta \vec l)_k\) dan \(~\vec r_k\) adalah, seperti sebelumnya, tegak lurus, oleh karena itu \(\sin \alpha = 1\) . Jadi cincin itu punya simetri aksial, maka vektor total induksi medan pada titik tersebut A harus diarahkan sepanjang sumbu cincin. Kesimpulan yang sama tentang arah vektor induksi total dapat dicapai jika kita memperhatikan bahwa setiap bagian cincin yang dipilih memiliki sisi simetris di sisi yang berlawanan, dan jumlah dua vektor simetris diarahkan sepanjang sumbu cincin. Jadi, untuk menentukan modulus vektor induksi total, perlu dijumlahkan proyeksi vektor-vektor tersebut ke sumbu cincin. Operasi ini tidak terlalu sulit jika kita memperhitungkan jarak dari semua titik ring ke titik pengamatan sama \(~r = r_k = \sqrt(R^2 + z^2)\) , dan sudutnya juga sama φ antara vektor \(~(\Delta \vec B)_k\) dan sumbu cincin. Mari kita tuliskan ekspresi modulus vektor induksi total yang diinginkan

\(~B = \sum_k \Delta B_(zk) = \sum_k \frac(\mu_0)(4 \pi) \frac((I \Delta l)_k)(r^2) \cos \varphi = \frac (\mu_0)(4 \pi) \frac(I \cos \varphi)(r^2) \sum_k (\Delta l)_k = \frac(\mu_0)(4 \pi) \frac(I \cos \ varphi)(r^2) 2 \pi R = \frac(\mu_0 I R)(2 r^2) \cos \varphi\) .

Dari gambar berikut bahwa \(~\cos \varphi = \frac(R)(r)\), dengan memperhitungkan persamaan jarak R, kita memperoleh ekspresi akhir untuk vektor induksi medan

\(~B = \frac(\mu_0 I R)(2 r^2) \cos \varphi = \frac(\mu_0 I R^2)(2 r^3) = \frac(\mu_0 I)(2) \ cdot \frac(R^2)((R^2 + z^2)^\frac(3)(2))\) . (3)

Seperti yang diharapkan, di tengah ring (di z= 0), rumus (3) berubah menjadi rumus (2) yang diperoleh sebelumnya.

Tugas untuk pekerjaan mandiri.

1. Gambarkan ketergantungan induksi medan (3) pada jarak ke pusat ring.
2. Bandingkan ketergantungan yang diperoleh (3) dengan ekspresi modulus kuat medan listrik yang diciptakan oleh cincin bermuatan seragam (§9.6). Jelaskan perbedaan mendasar antara ketergantungan ini.

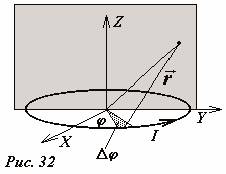
Dengan menggunakan metode umum yang dibahas di sini, dimungkinkan untuk menghitung induksi medan pada titik sembarang. Sistem yang dipertimbangkan mempunyai simetri aksial, sehingga cukup mencari sebaran medan pada bidang yang tegak lurus bidang cincin dan melalui pusatnya. Biarkan cincin itu tergeletak di pesawat xOy(Gbr. 32), dan bidang dihitung di bidang kamu Oz. Cincin harus dibagi menjadi beberapa bagian kecil yang terlihat dari tengah dengan sudut Δ φ dan jumlahkan bidang yang dibuat oleh bagian ini. Anda dapat menunjukkan ( Cobalah sendiri), bahwa komponen vektor induksi magnet dari medan yang ditimbulkan oleh satu elemen arus yang dipilih pada suatu titik dengan koordinat ( kamu,z) dihitung menggunakan rumus:

\(~\begin(matriks) r_k = \sqrt(x^2 + y^2 - 2xR \cos \varphi_k +1) ; \\ \Delta B_(yk) = -\frac(\mu_0)(4 \pi ) \frac(z \cos \varphi_k)(r^3_k) \Delta \varphi ; \\ \Delta B_(zk) = -\frac(\mu_0)(4 \pi) \frac(1 - y \cos \ varphi_k)(r^3_k) \Delta \varphi .\end(matriks)\) (4)

Penjumlahan yang diperlukan tidak dapat dilakukan secara analitis, karena ketika berpindah dari satu bagian ring ke bagian lain, jarak ke titik penjumlahan berubah. Oleh karena itu, cara “paling sederhana” untuk melakukan penjumlahan tersebut adalah dengan menggunakan komputer.

Jika nilai vektor induksi diketahui (atau setidaknya terdapat algoritma untuk menghitungnya) pada setiap titik, maka gambaran garis-garis medan magnet dapat dibuat. Jelas sekali bahwa algoritma untuk membangun garis gaya medan vektor tidak bergantung pada kandungan fisiknya, dan algoritma semacam itu telah kita bahas secara singkat ketika mempelajari elektrostatika.

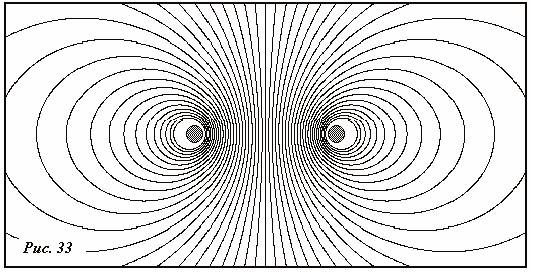
Pada Gambar. 33, pola garis medan dihitung dengan membagi cincin menjadi 20 bagian, ternyata cukup memadai, karena dengan 10 interval pembagian pun diperoleh pola yang hampir sama.

Mari kita perhatikan ekspresi induksi medan pada sumbu cincin pada jarak yang jauh lebih besar daripada jari-jari cincin z >> R. Dalam hal ini rumus (3) disederhanakan dan berbentuk

\(~B = \frac(\mu_0 I)(2) \cdot \frac(R^2)((R^2 + z^2)^\frac(3)(2)) \kira-kira \frac(\ mu_0 I)(2) \cdot \frac(R^2)(z^3) = \frac(\mu_0 I)(2 \pi) \cdot \frac(\pi R^2)(z^3) = \frac(\mu_0 p_m)(2 \pi z^3)\) , (5)

dimana \(I \pi R^2 = IS = p_m\) adalah hasil kali kuat arus dan luas rangkaian, yaitu momen magnet cincin. Rumusnya sama (kalau seperti biasa diganti μ 0 pada pembilangnya ε 0 pada penyebutnya) dengan ekspresi kuat medan listrik dipol pada sumbunya.

Kebetulan ini bukan suatu kebetulan; terlebih lagi, dapat ditunjukkan bahwa korespondensi tersebut berlaku untuk setiap titik di lapangan yang terletak pada jarak yang jauh dari ring. Faktanya, rangkaian kecil berarus adalah dipol magnet (dua elemen arus kecil yang identik dan berlawanan arah) - oleh karena itu medannya bertepatan dengan medan dipol listrik. Untuk menyoroti fakta ini lebih jelas, pada Gambar. Gambar 34 menunjukkan gambar garis-garis medan magnet cincin pada jarak yang jauh darinya ( bandingkan dengan gambar serupa untuk medan dipol listrik).

12.7.2 Medan magnet arus searah.

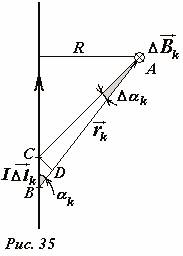
Mari kita hitung induksi medan magnet yang diciptakan oleh konduktor tak terbatas yang melaluinya arus listrik mengalir dengan gaya SAYA(Gbr. 35) Metode perhitungannya tetap sama: kita secara mental membagi konduktor menjadi beberapa bagian kecil \(~I \Delta \vec l_k\). Menurut hukum Biot-Savarre-Laplace pada titik sewenang-wenang A, terletak di kejauhan R dari sebuah konduktor, elemen arus sembarang menciptakan medan magnet, yang vektor induksinya \(~(\Delta \vec B)_k\) diarahkan tegak lurus terhadap bidang yang memuat konduktor dan titik yang dimaksud (pada Gambar 35 - tegak lurus terhadap bidang gambar), modulus vektor ini sama dengan

\(~\Delta B_k = \frac(\mu_0)(4 \pi) \frac(I \Delta l_k)(r^2_k) \sin \alpha_k\) , (1)

Di mana R k adalah jarak dari bagian konduktor yang dipilih ke titik pengamatan, α k adalah sudut antara konduktor dan arah dari elemen arus ke titik pengamatan.

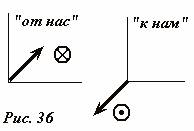
Mari kita sepakati perjanjian lain yang diterima secara umum. Seringkali Anda harus menggambar vektor yang tegak lurus terhadap bidang gambar. Dalam hal ini, vektor-vektor ini digambarkan dalam bentuk (Gbr. 36): lingkaran kecil dengan titik di tengahnya, jika vektor diarahkan “ke arah kita” (“tepi” vektor terlihat); lingkaran dengan garis bidik jika vektor diarahkan menjauhi kita (“bulu” vektor terlihat).

Vektor medan yang dibuat oleh semua bagian konduktor lainnya juga berarah, sehingga penjumlahan vektor dalam hal ini direduksi menjadi penjumlahan modulnya. Tetapi bahkan menghitung jumlah modul tidaklah mudah, karena jaraknya berbeda untuk setiap bagian konduktor R k dan α k berbeda. Meskipun demikian, penjumlahan seperti itu dapat dilakukan, hasilnya dinyatakan dengan rumus yang menentukan besarnya induksi medan magnet dari arus maju tak terhingga.

\(~B_k = \sum_k \Delta B_k = \sum_k \frac(\mu_0)(4 \pi) \frac(I \Delta l_k)(r^2_k) \sin \alpha_k = \frac(\mu_0 I)( 4 \pi) \sum_k (\frac(\Delta l_k)(r^2_k) \sin \alpha_k) = \frac(\mu_0 I)(2 \pi R)\) , (2)

perhitungan jumlah terakhir tidak diberikan di sini (yang sama dengan \(~\sum_k \frac(\Delta l_k)(r^2_k) \sin \alpha_k = \frac(2)(R)\)), untuk sekarang, percayalah pada keabsahan ekspresi yang dihasilkan, meskipun hanya karena memiliki makna fisik yang kaya. Pertama, rumus ini bertepatan dengan ekspresi kuat medan listrik yang diciptakan oleh garis lurus tak terhingga dari benang bermuatan seragam; kedua, ini sesuai dengan hasil eksperimen A.M. Ampere tentang studi interaksi arus paralel. Memang benar, jika suatu penghantar menimbulkan medan magnet yang induksinya berbanding terbalik dengan jarak ke penghantar, maka penghantar kedua dikenai gaya Ampere yang sebanding dengan induksi medan, yaitu berbanding terbalik dengan jarak antara para konduktor.

Sekarang mari kita turunkan rumus jumlah yang muncul pada persamaan (2). Hal ini paling sederhana diturunkan dengan menggunakan operasi integrasi, tetapi di sini kami akan memberikan penurunan geometriknya. Untuk memulainya, gunakan Gambar. 35 kita transformasikan setiap suku dari rumus ini \(~\frac(\Delta l_k)(r^2_k) \sin \alpha_k\) . Perhatikan bahwa hasil kali \(~\Delta l_k \sin \alpha_k\) sama dengan panjang segmen CD, tegak lurus terhadap vektor \(~\vec r_k\) - \(~\Delta l_k \sin \alpha_k = |CD|\) . Perbandingan panjang ruas tersebut dengan jaraknya R k untuk elemen arus yang panjangnya kecil sama dengan sudut kecil Δ α k, di mana bagian konduktor yang dipilih terlihat

\(~\frac(\Delta l_k)(r_k) \sin \alpha_k = \frac(|CD|)(r_k) = \Delta \alpha_k\) (3)

(lebih tepatnya perbandingan ini sama dengan garis singgung sudut, yang mana untuk sudut kecil sama dengan sudut itu sendiri, diukur dalam radian). Dari gambar yang sama dapat disimpulkan bahwa rasio \(~\frac(r_k)(\sin \alpha_k) = R\) sama dengan jarak dari titik pengamatan ke konduktor dan tidak bergantung pada pilihan bagian konduktor . Dengan mempertimbangkan hubungan dan rumus (2) ini, kita peroleh

\(~\frac(\Delta l_k)(r^2_k) \sin \alpha_k = \frac(\Delta \alpha_k)(r_k) = \frac(\Delta \alpha_k \sin \alpha_k)(R)\) .

Jadi, menghitung jumlah (2) dikurangi menjadi menghitung jumlah \(~\sum_k \Delta \alpha_k \sin \alpha_k\) , yang semua sudutnya kecil (oleh karena itu jumlah sukunya besar), misalkan sudutnya α k bervariasi dari nol hingga beberapa nilai pembatas α maks.

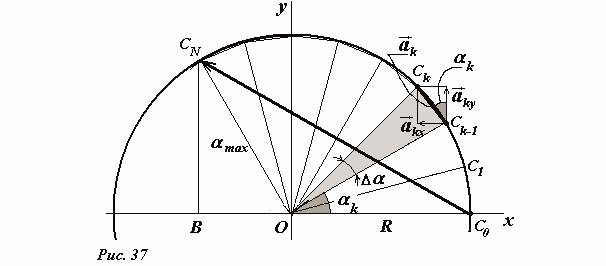
Untuk menghitung jumlah ini, kita akan menggunakan teknik buatan (kita akan menemukannya di masa depan). Mari kita ambil sebuah lingkaran (Gbr. 37) yang berjari-jari R dan memecahnya dengan titik-titik C 0 , C 1 , C 2 , …, C N untuk area kecil, ukuran sudut masing-masing sama dengan Δ α .

Tali busur yang dibentuk oleh titik-titik partisi akan dianggap sebagai vektor \(~\vec a_0 = \overrightarrow (C_0 C_1), \vec a_1 = \overrightarrow (C_1 C_2), \ldots, \vec a_k = \overrightarrow (C_k C_(k+ 1)), \ldots\) . Jumlah vektor-vektor ini jelas - ini adalah vektor \(~\vec A\) yang menghubungkan titik awal dan akhir partisi lingkaran:

\(~\sum_k \vec a_k = \overrightarrow (C_0 C_N) = \vec A\) . (4)

Sekarang, perhatian, jika persamaan vektor benar, maka ekspresi serupa juga berlaku untuk setiap proyeksi vektor-vektor ini. Mari kita perkenalkan sistem kartesius koordinat dengan titik asal di pusat lingkaran, sumbu Sapi yang melewati titik awal. Panjang vektor tertulis yang dibangun sama dengan \(~|\vec a_k| = R \Delta \alpha_k\) (lebih tepatnya, ini adalah panjang busur, tetapi untuk sudut kecil, panjang tali busur yang berkontraksi cenderung dengan panjang busur). Dari Gambar 37 dapat disimpulkan bahwa proyeksi vektor ini pada sumbu koordinat adalah sama,

\(~a_(kx) = -R \Delta \alpha_k \sin \alpha_k ; a_(ky) = R \Delta \alpha_k \cos \alpha_k\) .

Memproyeksikan persamaan (4) ke sumbu koordinat yang kita peroleh

\(~\begin(matriks) (\vec A)_x = (\overrightarrow (C_0 C_N))_x = -|C_0 B| = \sum_k a_(kx) = -\sum_k R \Delta \alpha_k \sin \alpha_k \\ (\vec A)_y = (\overrightarrow (C_0 C_N))_y = -|C_N B| = \sum_k a_(ky) = \sum_k R \Delta \alpha_k \cos \alpha_k \end(matriks) \) . (5)

Proyeksi vektor total \(~\vec A\) pada sumbu koordinat dapat ditemukan dengan mudah

\(~\begin(matriks) (\vec A)_x = (\overrightarrow (C_0 C_N))_x = -|C_0 B| = -(R + R \cos (\pi - \alpha_(max))) = R(1 - \cos \alpha_(max)) \\ (\vec A)_y = (\overrightarrow (C_0 C_N))_y = -|C_N B| = R \sin (\pi - \alpha_(max)) = R \sin \alpha_(max) \end(matriks) \) . (6)

Membandingkan ekspresi (5) dan (6) kita memperoleh rumus yang diperlukan

\(~\sum_k \sin \alpha_k \Delta \alpha_k = 1 - \cos \alpha_(max); \sum_k \cos \alpha_k \Delta \alpha_k = \sin \alpha_(max)\) . (7)

Mari kita tekankan sekali lagi bahwa penjumlahan dalam rumus-rumus ini dilakukan dalam batas perubahan sudut dari nol ke nilai batas. α maks.

Perlu diingat bahwa konduktor lurus tak terhingga terlihat dari titik mana pun di luarnya pada suatu sudut α maks = π , oleh karena itu jumlah yang dibutuhkan dinyatakan dengan rumus

\(~\jumlah_k \frac(\Delta l_k)(r^2_k) \sin \alpha_k = \sum_k \frac(\Delta \alpha_k \sin \alpha_k)(R) = \frac(1 - \cos \pi) (R) = \frac(2)(R)\) ,

Q.E.D.

Mari kita perkirakan panjang konduktor “tak terhingga” dalam hal ini - berapa kali panjang konduktor harus lebih besar dari jarak ke titik pengamatan agar kesalahan dalam menghitung induksi medan menggunakan rumus (2) diterapkan pada a konduktor dengan panjang terbatas akan diabaikan.

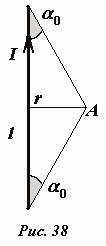
Misalkan panjang konduktor lurus adalah aku, dan induksi medan dihitung pada titik tersebut A, terletak di kejauhan R(kami percaya itu R << aku) dari pusat konduktor (Gbr. 38). Dengan menggunakan rumus yang diperoleh, seseorang dapat memperoleh ekspresi yang tepat untuk induksi medan pada titik yang dipertimbangkan \(~\bar(B) = \frac(\mu_0 I)(2 \pi r) \cos \alpha_0\) , di mana α 0 - sudut antara konduktor dan arah ke titik pengamatan dari ujung konduktor.

Jika kita menganggap konduktor itu panjangnya tak terhingga, maka induktansi medan harus dihitung menggunakan rumus (yang dalam hal ini harus dianggap sebagai perkiraan) \(~\tilde(B) = \frac(\mu_0 I)(2 \pi R)\) . Kesalahan relatif rumus ini sama dengan

\(~\varepsilon = \frac(\tilde(B) - \bar(B))(\bar(B)) = \frac(1)(\cos \alpha_0) - 1 = \frac(\sqrt(\ kiri (\frac(l)(2) \kanan)^2 + r^2))(\frac(l)(2)) - 1 = \sqrt(1 + 4 \frac(r^2)(l^ 2)) - 1 \kira-kira 2 \frac(r^2)(l^2)\) .

Kesalahan seperti itu akan terjadi jika perbandingan panjang konduktor dengan jarak ke titik pengamatan sama dengan \(~\frac(l)(r) = \frac(2)(\varepsilon)\). Jadi untuk kesalahan relatif ε = 1% rasio yang dibutuhkan adalah \(~\frac(l)(r) \kira-kira 15\). Jadi, dalam kasus yang dipertimbangkan, “tak terhingga” sama dengan 15.