eigenvalues ​​​​(संख्याएं) और eigenvectors। समाधान के उदाहरण। एक रैखिक ऑपरेटर के आइगेनवेक्टर और आइगेनवैल्यू

विकर्ण आव्यूहों की संरचना सबसे सरल होती है। सवाल उठता है कि क्या ऐसा आधार खोजना संभव है जिसमें रैखिक ऑपरेटर के मैट्रिक्स का विकर्ण रूप होगा। ऐसा आधार मौजूद है.
आइए हमें एक रैखिक स्थान R n और उसमें अभिनय करने वाला एक रैखिक संचालिका A दिया जाए; इस स्थिति में, ऑपरेटर A, R n को अपने में ले लेता है, अर्थात A:R n → R n ।

परिभाषा। एक गैर-शून्य वेक्टर को ऑपरेटर ए का आइजनवेक्टर कहा जाता है यदि ऑपरेटर ए एक कोलिनियर वेक्टर में अनुवाद करता है, अर्थात। संख्या λ को eigenvector के अनुरूप ऑपरेटर A का eigenvalue या eigenvalue कहा जाता है।
आइए हम eigenvalues ​​​​और eigenvectors के कुछ गुणों पर ध्यान दें।
1. eigenvectors का कोई भी रैखिक संयोजन समान eigenvalue λ के अनुरूप ऑपरेटर A समान eigenvalue वाला एक eigenvector है।
2. आइजेनवेक्टर ऑपरेटर A जोड़ीवार अलग-अलग eigenvalues ​​λ 1 , λ 2 , …, λ m के साथ रैखिक रूप से स्वतंत्र हैं।
3. यदि eigenvalues ​​​​λ 1 =λ 2 = λ m = λ, तो eigenvalue λ m से अधिक रैखिक रूप से स्वतंत्र eigenvectors से मेल नहीं खाता है।

तो, यदि n रैखिक रूप से स्वतंत्र eigenvectors हैं , विभिन्न eigenvalues ​​​​λ 1, λ 2, ..., λ n के अनुरूप, तो वे रैखिक रूप से स्वतंत्र हैं, इसलिए, उन्हें अंतरिक्ष R n के आधार के रूप में लिया जा सकता है। आइए हम इसके eigenvectors के आधार पर रैखिक ऑपरेटर A के मैट्रिक्स का रूप खोजें, जिसके लिए हम वैक्टर के आधार पर ऑपरेटर A के साथ कार्य करेंगे: तब .
इस प्रकार, इसके eigenvectors के आधार पर रैखिक ऑपरेटर A के मैट्रिक्स का एक विकर्ण रूप होता है, और ऑपरेटर A के eigenvalues ​​​​विकर्ण के साथ होते हैं।
क्या कोई अन्य आधार है जिसमें मैट्रिक्स का विकर्ण रूप होता है? इस प्रश्न का उत्तर निम्नलिखित प्रमेय द्वारा दिया गया है।

प्रमेय. आधार (i = 1..n) में एक रैखिक ऑपरेटर ए के मैट्रिक्स का एक विकर्ण रूप होता है यदि और केवल यदि आधार के सभी वैक्टर ऑपरेटर ए के आइजनवेक्टर होते हैं।

eigenvalues ​​​​और eigenvectors खोजने का नियम

. (*)

(1)
कहाँ - रैखिक ऑपरेटर मैट्रिक्स.

सिस्टम (1) का एक गैर-शून्य समाधान है यदि इसका निर्धारक डी शून्य के बराबर है

उदाहरण 12. रैखिक ऑपरेटर ए कानून के अनुसार आर 3 में कार्य करता है, जहां x 1, x 2, .., x n आधार में वेक्टर के निर्देशांक हैं , , . इस ऑपरेटर के eigenvalues ​​​​और eigenvectors खोजें।
समाधान। हम इस ऑपरेटर का मैट्रिक्स बनाते हैं:
.
हम eigenvectors के निर्देशांक निर्धारित करने के लिए एक प्रणाली बनाते हैं:

हम एक अभिलक्षणिक समीकरण बनाते हैं और उसे हल करते हैं:

.
λ 1,2 = -1, λ 3 = 3.
सिस्टम में λ = -1 प्रतिस्थापित करने पर, हमारे पास है:
या
क्योंकि , तो दो आश्रित चर और एक मुक्त चर हैं।
मान लीजिए कि x 1 एक स्वतंत्र अज्ञात है हम इस प्रणाली को किसी भी तरह से हल करते हैं और इस प्रणाली का सामान्य समाधान ढूंढते हैं: समाधान की मूल प्रणाली में एक समाधान होता है, क्योंकि n - r = 3 - 2 = 1.
eigenvalue λ = -1 के अनुरूप eigenvectors के सेट का रूप है:, जहां x 1 शून्य के अलावा कोई अन्य संख्या है। आइए इस सेट से एक वेक्टर चुनें, उदाहरण के लिए, x 1 = 1 रखते हुए: .
इसी प्रकार तर्क करते हुए, हम eigenvalue λ = 3 के अनुरूप eigenvector पाते हैं: .
अंतरिक्ष R 3 में, आधार में तीन रैखिक रूप से स्वतंत्र वैक्टर होते हैं, लेकिन हमें केवल दो रैखिक रूप से स्वतंत्र eigenvectors प्राप्त होते हैं, जिनसे R 3 में आधार की रचना नहीं की जा सकती है। नतीजतन, हम एक रैखिक ऑपरेटर के मैट्रिक्स ए को विकर्ण रूप में कम नहीं कर सकते हैं।

उदाहरण 13. एक मैट्रिक्स दिया गया .
1. सिद्ध कीजिए कि सदिश मैट्रिक्स A का एक eigenvector है। इस eigenvector के अनुरूप eigenvalue ज्ञात कीजिए।
2. एक आधार खोजें जिसमें मैट्रिक्स ए का विकर्ण रूप हो।
समाधान।
1. यदि , तो एक आइजनवेक्टर है

.
वेक्टर (1, 8, -1) एक आइजनवेक्टर है। आइगेनवैल्यू λ = -1.
मैट्रिक्स में eigenvectors से युक्त आधार में एक विकर्ण रूप होता है। उनमें से एक मशहूर है. आइए बाकी खोजें।
हम सिस्टम से eigenvectors की तलाश करते हैं:

विशेषता समीकरण: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
आइए eigenvalue λ = -3 के अनुरूप eigenvector ढूंढें:

इस प्रणाली के मैट्रिक्स की रैंक दो है और अज्ञात की संख्या के बराबर है, इसलिए इस प्रणाली का केवल शून्य समाधान x 1 = x 3 = 0 है। x 2 यहां शून्य के अलावा कुछ भी हो सकता है, उदाहरण के लिए, x 2 = 1. इस प्रकार, वेक्टर (0,1,0) λ = -3 के अनुरूप एक आइजनवेक्टर है। की जाँच करें:
.
यदि λ = 1, तो हमें सिस्टम प्राप्त होता है
मैट्रिक्स की रैंक दो है. हम अंतिम समीकरण को काट देते हैं।
माना x 3 एक स्वतंत्र अज्ञात है। तब x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
x 3 = 1 मानते हुए, हमारे पास (-3,-9,1) है - eigenvalue λ = 1 के अनुरूप एक eigenvector। जाँच करें:

.
चूँकि eigenvalues ​​​​वास्तविक और विशिष्ट हैं, उनके अनुरूप वेक्टर रैखिक रूप से स्वतंत्र हैं, इसलिए उन्हें R 3 में आधार के रूप में लिया जा सकता है। इस प्रकार, आधार में , , मैट्रिक्स ए का रूप है:
.
रैखिक ऑपरेटर A:R n → R n के प्रत्येक मैट्रिक्स को विकर्ण रूप में कम नहीं किया जा सकता है, क्योंकि कुछ रैखिक ऑपरेटरों के लिए n से कम रैखिक स्वतंत्र eigenvectors हो सकते हैं। हालाँकि, यदि मैट्रिक्स सममित है, तो बहुलता m के विशेषता समीकरण की जड़ बिल्कुल m रैखिक रूप से स्वतंत्र वैक्टर से मेल खाती है।

परिभाषा। एक सममित मैट्रिक्स एक वर्ग मैट्रिक्स है जिसमें मुख्य विकर्ण के बारे में सममित तत्व बराबर होते हैं, अर्थात।
टिप्पणियाँ। 1. सममित मैट्रिक्स के सभी eigenvalues ​​​​वास्तविक हैं।
2. जोड़ीवार अलग-अलग आइगेनवैल्यू के अनुरूप एक सममित मैट्रिक्स के आइजेनवेक्टर ऑर्थोगोनल हैं।
अध्ययन किए गए उपकरण के कई अनुप्रयोगों में से एक के रूप में, हम दूसरे क्रम के वक्र के प्रकार को निर्धारित करने की समस्या पर विचार करते हैं।

एक वर्ग मैट्रिक्स का एक आइजनवेक्टर वह होता है, जिसे किसी दिए गए मैट्रिक्स से गुणा करने पर एक संरेख वेक्टर प्राप्त होता है। सरल शब्दों में, जब एक मैट्रिक्स को एक आइजनवेक्टर से गुणा किया जाता है, तो बाद वाला वही रहता है, लेकिन एक निश्चित संख्या से गुणा किया जाता है।

परिभाषा

एक आइजनवेक्टर एक गैर-शून्य वेक्टर V है, जिसे वर्ग मैट्रिक्स M से गुणा करने पर, कुछ संख्या λ बढ़ जाने पर वह स्वयं बन जाता है। बीजगणितीय संकेतन में यह इस प्रकार दिखता है:

एम × वी = λ × वी,

जहां λ मैट्रिक्स एम का eigenvalue है।

आइए एक संख्यात्मक उदाहरण देखें. रिकॉर्डिंग में आसानी के लिए, मैट्रिक्स में संख्याओं को अर्धविराम से अलग किया जाएगा। आइए हमारे पास एक मैट्रिक्स है:

• एम = 0; 4;
• 6; 10.

आइए इसे कॉलम वेक्टर से गुणा करें:

• वी = -2;

जब हम किसी मैट्रिक्स को कॉलम वेक्टर से गुणा करते हैं, तो हमें एक कॉलम वेक्टर भी मिलता है। सख्त गणितीय भाषा में, 2 × 2 मैट्रिक्स को कॉलम वेक्टर से गुणा करने का सूत्र इस तरह दिखेगा:

• एम × वी = एम11 × वी11 + एम12 × वी21;
• एम21 × वी11 + एम22 × वी21।

M11 का अर्थ है मैट्रिक्स M का तत्व, पहली पंक्ति और पहले कॉलम में स्थित तत्व, और M22 दूसरी पंक्ति और दूसरे कॉलम में स्थित तत्व है। हमारे मैट्रिक्स के लिए, ये तत्व M11 = 0, M12 = 4, M21 = 6, M22 10 हैं। एक कॉलम वेक्टर के लिए, ये मान V11 = -2, V21 = 1 हैं। इस सूत्र के अनुसार, हमें निम्नलिखित मिलता है एक वेक्टर द्वारा एक वर्ग मैट्रिक्स के उत्पाद का परिणाम:

• एम × वी = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

सुविधा के लिए, आइए कॉलम वेक्टर को एक पंक्ति में लिखें। इसलिए, हमने वर्ग मैट्रिक्स को वेक्टर (-2; 1) से गुणा किया, जिसके परिणामस्वरूप वेक्टर (4; -2) प्राप्त हुआ। जाहिर है, यह वही वेक्टर है जिसे λ = -2 से गुणा किया गया है। इस मामले में लैम्ब्डा मैट्रिक्स के eigenvalue को दर्शाता है।

मैट्रिक्स का एक आइजनवेक्टर एक कोलिनियर वेक्टर होता है, यानी एक ऐसी वस्तु जो मैट्रिक्स से गुणा करने पर अंतरिक्ष में अपनी स्थिति नहीं बदलती है। वेक्टर बीजगणित में संरेखता की अवधारणा ज्यामिति में समानता शब्द के समान है। एक ज्यामितीय व्याख्या में, संरेख सदिश विभिन्न लंबाई के समानांतर निर्देशित खंड होते हैं। यूक्लिड के समय से, हम जानते हैं कि एक रेखा के समानांतर अनंत संख्या में रेखाएँ होती हैं, इसलिए यह मान लेना तर्कसंगत है कि प्रत्येक मैट्रिक्स में अनंत संख्या में आइजनवेक्टर होते हैं।

पिछले उदाहरण से, यह देखा जा सकता है कि (-8; 4), और (16; -8), और (32, -16) दोनों आइजनवेक्टर हो सकते हैं। ये सभी eigenvalue λ = -2 के अनुरूप संरेख सदिश हैं। जब मूल मैट्रिक्स को इन वैक्टरों से गुणा किया जाता है, तब भी हमें परिणाम के रूप में एक वेक्टर मिलेगा, जो मूल से 2 गुना भिन्न होता है। इसीलिए, आइजनवेक्टर खोजने की समस्याओं को हल करते समय, केवल रैखिक रूप से स्वतंत्र वेक्टर वस्तुओं को ढूंढना आवश्यक है। अक्सर, n × n मैट्रिक्स के लिए, eigenvectors की n-वीं संख्या होती है। हमारा कैलकुलेटर दूसरे क्रम के वर्ग आव्यूहों के विश्लेषण के लिए डिज़ाइन किया गया है, इसलिए परिणाम के रूप में लगभग हमेशा दो eigenvectors मिलेंगे, सिवाय इसके कि जब वे मेल खाते हों।

उपरोक्त उदाहरण में, हम मूल मैट्रिक्स के आइजेनवेक्टर को पहले से जानते थे और लैम्ब्डा संख्या को दृष्टिगत रूप से निर्धारित करते थे। हालाँकि, व्यवहार में, सब कुछ दूसरे तरीके से होता है: शुरुआत में eigenvalues ​​​​और उसके बाद ही eigenvectors होते हैं।

समाधान एल्गोरिथ्म

आइए मूल मैट्रिक्स M को फिर से देखें और इसके दोनों eigenvectors को खोजने का प्रयास करें। तो मैट्रिक्स इस तरह दिखता है:

• एम = 0; 4;
• 6; 10.

सबसे पहले हमें eigenvalue λ निर्धारित करने की आवश्यकता है, जिसके लिए निम्नलिखित मैट्रिक्स के निर्धारक की गणना करने की आवश्यकता है:

• (0 - λ); 4;
• 6; (10 − λ).

यह मैट्रिक्स मुख्य विकर्ण पर तत्वों से अज्ञात λ घटाकर प्राप्त किया जाता है। निर्धारक मानक सूत्र का उपयोग करके निर्धारित किया जाता है:

• detA = M11 × M21 − M12 × M22
• detA = (0 - λ) × (10 - λ) - 24

चूँकि हमारा वेक्टर गैर-शून्य होना चाहिए, हम परिणामी समीकरण को रैखिक रूप से निर्भर के रूप में स्वीकार करते हैं और अपने निर्धारक detA को शून्य के बराबर करते हैं।

(0 - λ) × (10 - λ) - 24 = 0

आइए कोष्ठक खोलें और मैट्रिक्स का अभिलक्षणिक समीकरण प्राप्त करें:

λ 2 − 10λ − 24 = 0

यह एक मानक द्विघात समीकरण है जिसे विवेचक का उपयोग करके हल करने की आवश्यकता है।

डी = बी 2 - 4एसी = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196

विवेचक का मूल sqrt(D) = 14 है, इसलिए λ1 = -2, λ2 = 12। अब प्रत्येक लैम्ब्डा मान के लिए हमें आइजेनवेक्टर खोजने की आवश्यकता है। आइए हम λ = -2 के लिए सिस्टम गुणांक व्यक्त करें।

• एम - λ × ई = 2; 4;
• 6; 12.

इस सूत्र में, E पहचान मैट्रिक्स है। परिणामी मैट्रिक्स के आधार पर, हम रैखिक समीकरणों की एक प्रणाली बनाते हैं:

2x + 4y = 6x + 12y,

जहां x और y आइजेनवेक्टर तत्व हैं।

आइए बाईं ओर के सभी X और दाईं ओर के सभी Y को एकत्रित करें। जाहिर है - 4x = 8y. व्यंजक को -4 से विभाजित करें और x = -2y प्राप्त करें। अब हम अज्ञात के किसी भी मान को लेते हुए, मैट्रिक्स का पहला आइजनवेक्टर निर्धारित कर सकते हैं (रैखिक रूप से निर्भर आइजनवेक्टरों की अनंतता को याद रखें)। आइए y = 1 लें, फिर x = -2. इसलिए, पहला आइजनवेक्टर V1 = (-2; 1) जैसा दिखता है। लेख की शुरुआत पर लौटें. यह वह वेक्टर ऑब्जेक्ट था जिसे हमने आइजेनवेक्टर की अवधारणा को प्रदर्शित करने के लिए मैट्रिक्स को गुणा किया था।

आइए अब λ = 12 के लिए आइजनवेक्टर खोजें।

• एम - λ × ई = -12; 4
• 6; -2.

आइए रैखिक समीकरणों की वही प्रणाली बनाएं;

• -12x + 4y = 6x − 2y
• -18x = -6y
• 3x = y.

अब हम x = 1 लेते हैं, इसलिए y = 3. इस प्रकार, दूसरा eigenvector V2 = (1; 3) जैसा दिखता है। मूल मैट्रिक्स को किसी दिए गए वेक्टर से गुणा करने पर, परिणाम हमेशा वही वेक्टर होगा जिसे 12 से गुणा किया जाएगा। यहीं पर समाधान एल्गोरिदम समाप्त होता है। अब आप जानते हैं कि मैट्रिक्स के आइजेनवेक्टर को मैन्युअल रूप से कैसे निर्धारित किया जाए।

• निर्धारक;
• ट्रेस, अर्थात्, मुख्य विकर्ण पर तत्वों का योग;
• रैंक, यानी, रैखिक रूप से स्वतंत्र पंक्तियों/स्तंभों की अधिकतम संख्या।

प्रोग्राम उपरोक्त एल्गोरिथम के अनुसार संचालित होता है, समाधान प्रक्रिया को यथासंभव छोटा करता है। यह बताना महत्वपूर्ण है कि प्रोग्राम में लैम्ब्डा को "सी" अक्षर द्वारा निर्दिष्ट किया जाता है। आइए एक संख्यात्मक उदाहरण देखें.

प्रोग्राम कैसे काम करता है इसका उदाहरण

आइए निम्नलिखित मैट्रिक्स के लिए eigenvectors निर्धारित करने का प्रयास करें:

• एम = 5; 13;
• 4; 14.

आइए इन मानों को कैलकुलेटर की कोशिकाओं में दर्ज करें और निम्नलिखित रूप में उत्तर प्राप्त करें:

• मैट्रिक्स रैंक: 2;
• मैट्रिक्स निर्धारक: 18;
• मैट्रिक्स ट्रेस: ​​19;
• आइजनवेक्टर की गणना: c 2 − 19.00c + 18.00 (विशेषता समीकरण);
• आइजेनवेक्टर गणना: 18 (पहला लैम्ब्डा मान);
• आइजेनवेक्टर गणना: 1 (दूसरा लैम्ब्डा मान);
• वेक्टर 1 के लिए समीकरणों की प्रणाली: -13x1 + 13y1 = 4x1 − 4y1;
• वेक्टर 2 के लिए समीकरणों की प्रणाली: 4x1 + 13y1 = 4x1 + 13y1;
• ईजेनवेक्टर 1: (1; 1);
• आइजेनवेक्टर 2: (-3.25; 1).

इस प्रकार, हमें दो रैखिक रूप से स्वतंत्र eigenvectors प्राप्त हुए।

निष्कर्ष

रैखिक बीजगणित और विश्लेषणात्मक ज्यामिति किसी भी नए इंजीनियरिंग प्रमुख के लिए मानक विषय हैं। वैक्टर और मैट्रिक्स की बड़ी संख्या भयावह है, और ऐसी बोझिल गणनाओं में गलतियाँ करना आसान है। हमारा कार्यक्रम छात्रों को अपनी गणनाओं की जांच करने या ईजेनवेक्टर खोजने की समस्या को स्वचालित रूप से हल करने की अनुमति देगा। हमारे कैटलॉग में अन्य रैखिक बीजगणित कैलकुलेटर हैं; उन्हें अपने अध्ययन या कार्य में उपयोग करें।

www.साइटआपको खोजने की अनुमति देता है। साइट गणना करती है. कुछ ही सेकंड में सर्वर सही समाधान दे देगा। मैट्रिक्स के लिए विशेषता समीकरणसारणिक की गणना के लिए नियम का उपयोग करके पाया गया एक बीजगणितीय अभिव्यक्ति होगी मैट्रिक्स मैट्रिक्स, जबकि मुख्य विकर्ण के साथ विकर्ण तत्वों और चर के मूल्यों में अंतर होगा। गणना करते समय मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरण, प्रत्येक तत्व मैट्रिक्ससंगत अन्य तत्वों से गुणा किया जाएगा मैट्रिक्स. मोड में खोजें ऑनलाइनकेवल वर्ग के लिए संभव है मैट्रिक्स. ऑपरेशन खोजें मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरणतत्वों के गुणनफल के बीजगणितीय योग की गणना करना कम कर देता है मैट्रिक्सनिर्धारक को खोजने के परिणामस्वरूप मैट्रिक्स, केवल निर्धारण के उद्देश्य से मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरण. यह ऑपरेशन सिद्धांत में एक विशेष स्थान रखता है मैट्रिक्स, आपको जड़ों का उपयोग करके eigenvalues ​​​​और वैक्टर खोजने की अनुमति देता है। ढूँढने का कार्य मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरणगुणनकारी तत्वों से मिलकर बना है मैट्रिक्सइसके बाद एक निश्चित नियम के अनुसार इन उत्पादों का योग किया जाता है। www.साइटढूंढता है मैट्रिक्स के लिए विशेषता समीकरणमोड में दिया गया आयाम ऑनलाइन. गणना मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरणइसके आयाम को देखते हुए, यह संख्यात्मक या प्रतीकात्मक गुणांक के साथ एक बहुपद ढूंढना है, जो निर्धारक की गणना के नियम के अनुसार पाया जाता है मैट्रिक्स- संबंधित तत्वों के उत्पादों के योग के रूप में मैट्रिक्स, केवल निर्धारण के उद्देश्य से मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरण. एक द्विघात के लिए एक चर के संबंध में एक बहुपद ढूँढना मैट्रिक्स, परिभाषा के रूप में मैट्रिक्स के लिए विशेषता समीकरण, सिद्धांत में सामान्य मैट्रिक्स. बहुपद के मूल का अर्थ मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरणके लिए eigenvectors और eigenvalues ​​​​निर्धारित करने के लिए उपयोग किया जाता है मैट्रिक्स. इसके अलावा, यदि निर्धारक मैट्रिक्सतब शून्य के बराबर होगा मैट्रिक्स की विशेषता समीकरणविपरीत के विपरीत, अभी भी अस्तित्व में रहेगा मैट्रिक्स. गणना करने के लिए मैट्रिक्स के लिए विशेषता समीकरणया एक साथ कई खोजें मैट्रिक्स विशेषता समीकरण, आपको बहुत अधिक समय और प्रयास खर्च करने की आवश्यकता है, जबकि हमारा सर्वर कुछ ही सेकंड में इसे ढूंढ लेगा मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरण. इस मामले में, खोजने का उत्तर मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरणसही और पर्याप्त सटीकता के साथ होगा, भले ही खोजते समय संख्याएँ हों मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरणतर्कहीन होगा. स्थल पर www.साइटतत्वों में वर्ण प्रविष्टियों की अनुमति है मैट्रिक्स, वह है मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरणगणना करते समय सामान्य प्रतीकात्मक रूप में दर्शाया जा सकता है मैट्रिक्स की विशेषता समीकरण ऑनलाइन. खोजने की समस्या को हल करते समय प्राप्त उत्तर की जाँच करना उपयोगी होता है मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरणसाइट का उपयोग करना www.साइट. बहुपद की गणना का कार्य करते समय - मैट्रिक्स की विशेषता समीकरण, इस समस्या को हल करते समय आपको सावधान रहने और अत्यधिक ध्यान केंद्रित करने की आवश्यकता है। बदले में, हमारी साइट आपको विषय पर अपना निर्णय जांचने में मदद करेगी एक मैट्रिक्स का अभिलक्षणिक समीकरण ऑनलाइन. यदि आपके पास हल की गई समस्याओं की लंबी जांच के लिए समय नहीं है, तो www.साइटखोजने और गणना करते समय जाँच करने के लिए यह निश्चित रूप से एक सुविधाजनक उपकरण होगा मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरण.

सजातीय रैखिक समीकरणों की प्रणाली

सजातीय रैखिक समीकरणों की एक प्रणाली रूप की एक प्रणाली है

इस मामले में यह स्पष्ट है , क्योंकि इन निर्धारकों में से किसी एक स्तंभ के सभी तत्व शून्य के बराबर हैं।

चूँकि अज्ञात सूत्रों के अनुसार ज्ञात किये जाते हैं , तो उस स्थिति में जब Δ ≠ 0, सिस्टम में एक अद्वितीय शून्य समाधान होता है एक्स = य = जेड= 0. हालाँकि, कई समस्याओं में दिलचस्प सवाल यह है कि क्या एक सजातीय प्रणाली में शून्य के अलावा अन्य समाधान हैं।

प्रमेय.रैखिक सजातीय समीकरणों की एक प्रणाली के लिए एक गैर-शून्य समाधान होना आवश्यक और पर्याप्त है Δ ≠ 0.

इसलिए, यदि निर्धारक Δ ≠ 0 है, तो सिस्टम के पास एक अद्वितीय समाधान है। यदि Δ ≠ 0, तो रैखिक सजातीय समीकरणों की प्रणाली में अनंत संख्या में समाधान होते हैं।

उदाहरण।

मैट्रिक्स के आइजनवेक्टर और आइगेनवैल्यू

मान लीजिए कि एक वर्गाकार मैट्रिक्स दिया गया है , एक्स- कुछ मैट्रिक्स-कॉलम, जिसकी ऊंचाई मैट्रिक्स के क्रम से मेल खाती है ए. .

कई समस्याओं में हमें समीकरण पर विचार करना पड़ता है एक्स

जहां λ कुछ संख्या है. यह स्पष्ट है कि किसी भी λ के लिए इस समीकरण का शून्य समाधान है।

वह संख्या λ जिसके लिए इस समीकरण का गैर-शून्य समाधान होता है, कहलाती है eigenvalueमैट्रिक्स ए, ए एक्सऐसे के लिए λ कहा जाता है आइजन्वेक्टरमैट्रिक्स ए.

आइए मैट्रिक्स का eigenvector खोजें ए. क्योंकि इ∙एक्स = एक्स, तो मैट्रिक्स समीकरण को फिर से लिखा जा सकता है या . विस्तारित रूप में, इस समीकरण को रैखिक समीकरणों की एक प्रणाली के रूप में फिर से लिखा जा सकता है। वास्तव में .

और इसलिए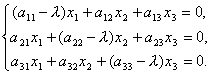

तो, हमें निर्देशांक निर्धारित करने के लिए सजातीय रैखिक समीकरणों की एक प्रणाली मिली एक्स 1, एक्स 2, एक्स 3वेक्टर एक्स. सिस्टम में गैर-शून्य समाधान होने के लिए, यह आवश्यक और पर्याप्त है कि सिस्टम का निर्धारक शून्य के बराबर हो, यानी।

यह λ के लिए तीसरी डिग्री का समीकरण है। यह कहा जाता है विशेषता समीकरणमैट्रिक्स एऔर λ के eigenvalues ​​​​को निर्धारित करने का कार्य करता है।

प्रत्येक eigenvalue λ एक eigenvector से मेल खाता है एक्स, जिनके निर्देशांक λ के संगत मान पर सिस्टम से निर्धारित होते हैं।

उदाहरण।

वेक्टर बीजगणित. वेक्टर की अवधारणा

भौतिकी की विभिन्न शाखाओं का अध्ययन करते समय, ऐसी मात्राएँ होती हैं जो पूरी तरह से उनके संख्यात्मक मानों को निर्दिष्ट करके निर्धारित की जाती हैं, उदाहरण के लिए, लंबाई, क्षेत्र, द्रव्यमान, तापमान, आदि। ऐसी मात्राएँ अदिश कहलाती हैं। हालाँकि, उनके अलावा, ऐसी मात्राएँ भी हैं, जिन्हें निर्धारित करने के लिए, संख्यात्मक मान के अलावा, अंतरिक्ष में उनकी दिशा जानना भी आवश्यक है, उदाहरण के लिए, शरीर पर लगने वाला बल, गति और त्वरण। जब कोई पिंड अंतरिक्ष में घूमता है, तो अंतरिक्ष में किसी दिए गए बिंदु पर चुंबकीय क्षेत्र की ताकत आदि। ऐसी मात्राएँ सदिश राशियाँ कहलाती हैं।

आइए एक सख्त परिभाषा पेश करें।

दिशात्मक खंडआइए एक खंड कहते हैं, जिसके सिरों के सापेक्ष यह ज्ञात होता है कि उनमें से कौन सा पहला है और कौन सा दूसरा है।

वेक्टरएक निश्चित लंबाई वाला निर्देशित खंड कहा जाता है, अर्थात। यह एक निश्चित लंबाई का एक खंड है, जिसमें इसे सीमित करने वाले बिंदुओं में से एक को शुरुआत के रूप में लिया जाता है, और दूसरे को अंत के रूप में लिया जाता है। अगर एवेक्टर की शुरुआत है, बीइसका अंत है, तो वेक्टर को प्रतीक द्वारा दर्शाया जाता है, इसके अलावा, वेक्टर को अक्सर एक अक्षर द्वारा दर्शाया जाता है। चित्र में, वेक्टर को एक खंड द्वारा और इसकी दिशा को एक तीर द्वारा दर्शाया गया है।

मापांकया लंबाईएक वेक्टर को निर्देशित खंड की लंबाई कहा जाता है जो इसे परिभाषित करता है। || द्वारा निरूपित या ||

तथाकथित शून्य वेक्टर, जिसका आरंभ और अंत मेल खाता है, को भी वेक्टर कहा जाएगा। इसे चिन्हित किया गया है. शून्य वेक्टर की कोई विशिष्ट दिशा नहीं होती है और इसका मापांक शून्य ||=0 होता है।

वेक्टर और कहलाते हैं समरेख, यदि वे एक ही रेखा पर या समानांतर रेखाओं पर स्थित हों। इसके अलावा, यदि सदिश और एक ही दिशा में हैं, तो हम विपरीत लिखेंगे।

एक ही तल के समांतर सीधी रेखाओं पर स्थित सदिश कहलाते हैं समतलीय.

दो वेक्टर कहलाते हैं बराबर, यदि वे संरेख हैं, उनकी दिशा समान है और लंबाई समान है। इस मामले में वे लिखते हैं.

सदिशों की समानता की परिभाषा से यह निष्कर्ष निकलता है कि एक सदिश को अंतरिक्ष में किसी भी बिंदु पर अपनी उत्पत्ति रखते हुए, स्वयं के समानांतर ले जाया जा सकता है।

उदाहरण के लिए.

वेक्टरों पर रैखिक संचालन

1. किसी सदिश को किसी संख्या से गुणा करना.

   एक सदिश और संख्या λ का गुणनफल एक नया सदिश है जैसे:

   एक सदिश और एक संख्या λ के गुणनफल को द्वारा दर्शाया जाता है।

   

   उदाहरण के लिए,एक वेक्टर है जो वेक्टर के समान दिशा में निर्देशित है और इसकी लंबाई वेक्टर की आधी है।

   प्रस्तुत ऑपरेशन में निम्नलिखित हैं गुण:

2. वेक्टर जोड़.

   मान लीजिए और दो मनमाना सदिश हैं। आइए एक मनमाना बिंदु लें हेऔर एक वेक्टर का निर्माण करें। उसके बाद बिंदु से एआइए वेक्टर को एक तरफ रख दें। पहले वेक्टर की शुरुआत को दूसरे वेक्टर के अंत से जोड़ने वाले वेक्टर को कहा जाता है जोड़इन सदिशों का और निरूपित किया जाता है .

   

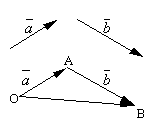
   सदिश योग की सूत्रबद्ध परिभाषा कहलाती है समांतर चतुर्भुज नियम, चूँकि सदिशों का समान योग निम्नानुसार प्राप्त किया जा सकता है। बिंदु से अलग रख दें हेवेक्टर और . आइए इन सदिशों पर एक समांतर चतुर्भुज बनाएं OABC. चूँकि सदिश, तो सदिश, जो शीर्ष से खींचे गए समांतर चतुर्भुज का विकर्ण है हे, स्पष्टतः सदिशों का योग होगा।

   

   निम्नलिखित की जाँच करना आसान है वेक्टर जोड़ के गुण.

3. वेक्टर अंतर.

   किसी दिए गए वेक्टर के संरेख, लंबाई में बराबर और विपरीत दिशा में निर्देशित वेक्टर को कहा जाता है विलोमएक सदिश के लिए सदिश और द्वारा निरूपित किया जाता है। विपरीत वेक्टर को वेक्टर को संख्या λ = -1: से गुणा करने के परिणाम के रूप में माना जा सकता है।

मैट्रिक्स A के साथ, यदि कोई संख्या l ऐसी है कि AX = lX है।

इस स्थिति में, संख्या l कहा जाता है eigenvalueऑपरेटर (मैट्रिक्स ए) वेक्टर एक्स के अनुरूप।

दूसरे शब्दों में, एक आइजनवेक्टर एक वेक्टर है, जो एक रैखिक ऑपरेटर की कार्रवाई के तहत, एक कोलीनियर वेक्टर में बदल जाता है, यानी। बस किसी संख्या से गुणा करें। इसके विपरीत, अनुचित वैक्टर को बदलना अधिक जटिल होता है।

आइए समीकरणों की एक प्रणाली के रूप में एक आइजनवेक्टर की परिभाषा लिखें:

आइए सभी शर्तों को बाईं ओर ले जाएँ:

बाद वाली प्रणाली को मैट्रिक्स रूप में इस प्रकार लिखा जा सकता है:

(ए - एलई)एक्स = ओ

परिणामी प्रणाली में हमेशा शून्य समाधान X = O होता है। ऐसी प्रणाली जिसमें सभी मुक्त पद शून्य के बराबर होते हैं, कहलाते हैं सजातीय. यदि ऐसी प्रणाली का मैट्रिक्स वर्गाकार है और इसका निर्धारक शून्य के बराबर नहीं है, तो क्रैमर के सूत्रों का उपयोग करके हमें हमेशा एक अद्वितीय समाधान मिलेगा - शून्य। यह साबित किया जा सकता है कि किसी सिस्टम में गैर-शून्य समाधान होते हैं यदि और केवल तभी जब इस मैट्रिक्स का निर्धारक शून्य के बराबर हो, यानी।

|ए - एलई| = = 0

अज्ञात एल वाले इस समीकरण को कहा जाता है विशेषता समीकरण (विशेषता बहुपद) मैट्रिक्स ए (रैखिक ऑपरेटर)।

यह सिद्ध किया जा सकता है कि एक रैखिक संकारक का अभिलक्षणिक बहुपद आधार की पसंद पर निर्भर नहीं करता है।

उदाहरण के लिए, आइए मैट्रिक्स A = द्वारा परिभाषित रैखिक ऑपरेटर के eigenvalues ​​​​और eigenvectors ढूंढें।

ऐसा करने के लिए, आइए एक अभिलक्षणिक समीकरण बनाएं |A - lE| = = (1 - एल) 2 - 36 = 1 - 2एल + एल 2 - 36 = एल 2 - 2एल - 35 = 0; डी = 4 + 140 = 144; eigenvalues ​​​​l 1 = (2 - 12)/2 = -5; एल 2 = (2 + 12)/2 = 7।

आइजनवेक्टर खोजने के लिए, हम समीकरणों की दो प्रणालियों को हल करते हैं

(ए + 5ई) एक्स = ओ

(ए - 7ई) एक्स = ओ

उनमें से पहले के लिए, विस्तारित मैट्रिक्स रूप लेता है

,

जहां से x 2 = c, x 1 + (2/3)c = 0; x 1 = - (2/3) s, अर्थात्। एक्स (1) = (- (2/3) एस; एस)।

उनमें से दूसरे के लिए, विस्तारित मैट्रिक्स रूप लेता है

,

जहाँ से x 2 = c 1, x 1 - (2/3)c 1 = 0; x 1 = (2/3)s 1, यानी। एक्स (2) = ((2/3)एस 1; एस 1)।

इस प्रकार, इस रैखिक ऑपरेटर के eigenvectors eigenvalue (-5) के साथ फॉर्म (-(2/3)с; с) के सभी वैक्टर हैं और फॉर्म के सभी वैक्टर ((2/3)с 1 ; с 1) के साथ हैं eigenvalue 7 .

यह सिद्ध किया जा सकता है कि ऑपरेटर ए का मैट्रिक्स इसके आइजेनवेक्टरों से युक्त आधार में विकर्ण है और इसका रूप है:

,

जहाँ l i इस मैट्रिक्स के eigenvalues ​​हैं।

इसका विपरीत भी सत्य है: यदि किसी आधार पर मैट्रिक्स A विकर्ण है, तो इस आधार के सभी वैक्टर इस मैट्रिक्स के eigenvectors होंगे।

यह भी सिद्ध किया जा सकता है कि यदि एक रैखिक ऑपरेटर के पास n जोड़ीवार अलग-अलग eigenvalues ​​हैं, तो संबंधित eigenvectors रैखिक रूप से स्वतंत्र हैं, और संबंधित आधार में इस ऑपरेटर के मैट्रिक्स का एक विकर्ण रूप है।

आइए इसे पिछले उदाहरण से स्पष्ट करें। आइए मनमाना गैर-शून्य मान c और c 1 लें, लेकिन ऐसे कि सदिश X (1) और X (2) रैखिक रूप से स्वतंत्र हों, अर्थात। एक आधार बनेगा. उदाहरण के लिए, मान लीजिए c = c 1 = 3, फिर X (1) = (-2; 3), X (2) = (2; 3)।

आइए हम इन वैक्टरों की रैखिक स्वतंत्रता को सत्यापित करें:

12 ≠ 0. इस नए आधार में, मैट्रिक्स A, A * = का रूप लेगा।

इसे सत्यापित करने के लिए, आइए सूत्र A * = C -1 AC का उपयोग करें। सबसे पहले, आइए C-1 खोजें।

सी -1 = ;

द्विघात आकार

द्विघात आकार n चरों के f(x 1, x 2, x n) को एक योग कहा जाता है, जिसका प्रत्येक पद या तो किसी एक चर का वर्ग होता है, या दो अलग-अलग चरों का गुणनफल होता है, जो एक निश्चित गुणांक के साथ लिया जाता है: f(x 1) , एक्स 2, एक्स एन) = (ए आईजे = ए जी)।

इन गुणांकों से बने मैट्रिक्स ए को कहा जाता है आव्यूहद्विघात रूप. यह हमेशा के लिए है सममितमैट्रिक्स (अर्थात् मुख्य विकर्ण के बारे में सममित मैट्रिक्स, a ij = a ji)।

मैट्रिक्स नोटेशन में, द्विघात रूप f(X) = X T AX है, जहां

वास्तव में

उदाहरण के लिए, आइए द्विघात रूप को मैट्रिक्स रूप में लिखें।

ऐसा करने के लिए, हमें द्विघात रूप का एक मैट्रिक्स मिलता है। इसके विकर्ण तत्व वर्ग चर के गुणांक के बराबर हैं, और शेष तत्व द्विघात रूप के संबंधित गुणांक के आधे के बराबर हैं। इसीलिए

मान लीजिए कि चर X का मैट्रिक्स-कॉलम मैट्रिक्स-कॉलम Y के गैर-अपक्षयी रैखिक परिवर्तन द्वारा प्राप्त किया जाता है, अर्थात। X = CY, जहां C nवें क्रम का एक गैर-एकवचन मैट्रिक्स है। फिर द्विघात रूप f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

इस प्रकार, एक गैर-अपक्षयी रैखिक परिवर्तन सी के साथ, द्विघात रूप का मैट्रिक्स रूप लेता है: ए * = सी टी एसी।

उदाहरण के लिए, आइए रैखिक परिवर्तन द्वारा द्विघात रूप f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 से प्राप्त द्विघात रूप f(y 1, y 2) खोजें।

द्विघात रूप कहा जाता है कैनन का(यह है विहित दृश्य), यदि इसके सभी गुणांक i ≠ j के लिए ij = 0 हैं, अर्थात।
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =।

इसका मैट्रिक्स विकर्ण है.

प्रमेय(प्रमाण यहां नहीं दिया गया है). किसी भी द्विघात रूप को गैर-अपक्षयी रैखिक परिवर्तन का उपयोग करके विहित रूप में कम किया जा सकता है।

उदाहरण के लिए, आइए हम द्विघात रूप को विहित रूप में कम करें
f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

ऐसा करने के लिए, पहले चर x 1 के साथ एक पूर्ण वर्ग का चयन करें:

f(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 = 2(x 1 + x 2) 2 - 5x 2 2 - x 2 x 3.

अब हम वेरिएबल x 2 के साथ एक पूर्ण वर्ग का चयन करते हैं:

f(x 1, x 2, x 3) = 2(x 1 + x 2) 2 - 5(x 2 2 + 2* x 2 *(1/10)x 3 + (1/100)x 3 2) + (5/100)x 3 2 =
= 2(x 1 + x 2) 2 - 5(x 2 - (1/10)x 3) 2 + (1/20)x 3 2।

फिर गैर-अपक्षयी रैखिक परिवर्तन y 1 = x 1 + x 2, y 2 = x 2 + (1/10)x 3 और y 3 = x 3 इस द्विघात रूप को विहित रूप f(y 1, y 2) में लाता है , y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2।

ध्यान दें कि द्विघात रूप का विहित रूप अस्पष्ट रूप से निर्धारित किया जाता है (एक ही द्विघात रूप को अलग-अलग तरीकों से विहित रूप में घटाया जा सकता है)। हालाँकि, विभिन्न तरीकों से प्राप्त विहित रूपों में कई सामान्य गुण होते हैं। विशेष रूप से, द्विघात रूप के सकारात्मक (नकारात्मक) गुणांक वाले पदों की संख्या फॉर्म को इस रूप में कम करने की विधि पर निर्भर नहीं करती है (उदाहरण के लिए, विचार किए गए उदाहरण में हमेशा दो नकारात्मक और एक सकारात्मक गुणांक होगा)। इस गुण को द्विघात रूपों की जड़ता का नियम कहा जाता है।

आइए हम उसी द्विघात रूप को एक अलग तरीके से विहित रूप में लाकर इसे सत्यापित करें। आइए वेरिएबल x 2 से परिवर्तन शुरू करें:

f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3(x 2 2 +
+ 2* x 2 ((1/6) x 3 - (2/3)x 1) + ((1/6) x 3 - (2/3)x 1) 2) + 3((1/6) x 3 - (2/3)x 1) 2 + 2x 1 2 =
= -3(x 2 + (1/6) x 3 - (2/3)x 1) 2 + 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 = एफ (y 1 , y 2 , y 3) = -3y 1 2 -
+3y 2 2 + 2y 3 2, जहां y 1 = - (2/3)x 1 + x 2 + (1/6) x 3, y 2 = (2/3)x 1 + (1/6) x 3 और y 3 = x 1 . यहां y 1 पर एक नकारात्मक गुणांक -3 है और y 2 और y 3 पर दो सकारात्मक गुणांक 3 और 2 हैं (और एक अन्य विधि का उपयोग करके हमें y 2 पर एक नकारात्मक गुणांक (-5) और दो सकारात्मक गुणांक प्राप्त हुए हैं: y 1 पर 2 और 1/20 y 3 पर)।

यह भी ध्यान दिया जाना चाहिए कि द्विघात रूप के मैट्रिक्स की रैंक को कहा जाता है द्विघात रूप की श्रेणी, विहित रूप के गैर-शून्य गुणांकों की संख्या के बराबर है और रैखिक परिवर्तनों के तहत नहीं बदलता है।

द्विघात रूप f(X) कहलाता है सकारात्मक (नकारात्मक) निश्चित, यदि चर के सभी मानों के लिए जो एक साथ शून्य के बराबर नहीं हैं, तो यह सकारात्मक है, अर्थात। f(X) > 0 (नकारात्मक, अर्थात)
एफ(एक्स)< 0).

उदाहरण के लिए, द्विघात रूप f 1 (X) = x 1 2 + x 2 2 सकारात्मक निश्चित है, क्योंकि वर्गों का योग है, और द्विघात रूप f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 ऋणात्मक निश्चित है, क्योंकि इसे f 2 (X) = -(x 1 - x 2) 2 के रूप में दर्शाया जा सकता है।

अधिकांश व्यावहारिक स्थितियों में, द्विघात रूप का निश्चित चिह्न स्थापित करना कुछ अधिक कठिन होता है, इसलिए इसके लिए हम निम्नलिखित प्रमेयों में से एक का उपयोग करते हैं (हम उन्हें बिना प्रमाण के तैयार करेंगे)।

प्रमेय. एक द्विघात रूप सकारात्मक (नकारात्मक) निश्चित है यदि और केवल तभी जब इसके मैट्रिक्स के सभी eigenvalues ​​​​सकारात्मक (नकारात्मक) हों।

प्रमेय(सिल्वेस्टर मानदंड)। एक द्विघात रूप सकारात्मक निश्चित होता है यदि और केवल तभी जब इस फॉर्म के मैट्रिक्स के सभी प्रमुख अवयस्क सकारात्मक हों।

मुख्य (कोना) लघु nवें क्रम के kवें क्रम के मैट्रिक्स A को मैट्रिक्स का निर्धारक कहा जाता है, जो मैट्रिक्स A () की पहली k पंक्तियों और स्तंभों से बना होता है।

ध्यान दें कि नकारात्मक निश्चित द्विघात रूपों के लिए मुख्य लघु के चिह्न वैकल्पिक होते हैं, और प्रथम-क्रम लघु ऋणात्मक होना चाहिए।

उदाहरण के लिए, आइए चिह्न निश्चितता के लिए द्विघात रूप f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 की जांच करें।

= (2 - एल)*
*(3 - एल) - 4 = (6 - 2एल - 3एल + एल 2) - 4 = एल 2 - 5एल + 2 = 0; डी = 25 - 8 = 17;
. अत: द्विघात रूप सकारात्मक निश्चित है।

विधि 2. मैट्रिक्स के पहले क्रम का मुख्य लघु A D 1 = a 11 = 2 > 0. दूसरे क्रम का मुख्य लघु D 2 = = 6 - 4 = 2 > 0. इसलिए, सिल्वेस्टर की कसौटी के अनुसार, द्विघात रूप है सकारात्मक रूप से निश्चित।

हम चिह्न निश्चितता के लिए एक और द्विघात रूप की जांच करते हैं, f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2।

विधि 1. आइए द्विघात रूप A = का एक मैट्रिक्स बनाएं। चारित्रिक समीकरण का स्वरूप होगा = (-2 - एल)*
*(-3 - एल) - 4 = (6 + 2एल + 3एल + एल 2) - 4 = एल 2 + 5एल + 2 = 0; डी = 25 - 8 = 17;
. अत: द्विघात रूप ऋणात्मक निश्चित है।

विधि 2. मैट्रिक्स के प्रथम क्रम का मुख्य लघु A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. नतीजतन, सिल्वेस्टर की कसौटी के अनुसार, द्विघात रूप नकारात्मक निश्चित है (मुख्य नाबालिगों के संकेत वैकल्पिक हैं, ऋण से शुरू होते हैं)।

और एक अन्य उदाहरण के रूप में, हम चिह्न-निर्धारित द्विघात रूप f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 की जांच करते हैं।

विधि 1. आइए द्विघात रूप A = का एक मैट्रिक्स बनाएं। चारित्रिक समीकरण का स्वरूप होगा = (2 - एल)*
*(-3 - एल) - 4 = (-6 - 2एल + 3एल + एल 2) - 4 = एल 2 + एल - 10 = 0; डी = 1 + 40 = 41;
.

इनमें से एक संख्या ऋणात्मक है और दूसरी सकारात्मक है। eigenvalues ​​​​के संकेत अलग-अलग हैं। नतीजतन, द्विघात रूप न तो नकारात्मक और न ही सकारात्मक रूप से निश्चित हो सकता है, यानी। यह द्विघात रूप चिह्न-निश्चित नहीं है (यह किसी भी चिह्न का मान ले सकता है)।

विधि 2. मैट्रिक्स के पहले क्रम का मुख्य लघु A D 1 = a 11 = 2 > 0. दूसरे क्रम का मुख्य लघु D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).