Nilai eigen (angka) dan vektor eigen Contoh solusi. Vektor eigen dan nilai eigen dari operator linier

Matriks diagonal mempunyai struktur yang paling sederhana. Timbul pertanyaan apakah mungkin menemukan basis yang matriks operator liniernya berbentuk diagonal. Dasar seperti itu memang ada.
Mari kita diberi ruang linier R n dan operator linier A yang bekerja di dalamnya; dalam hal ini, operator A mengambil R n ke dalam dirinya sendiri, yaitu A:R n → R n .

Definisi. Vektor bukan nol disebut vektor eigen dari operator A jika operator A diubah menjadi vektor kolinear, yaitu. Bilangan λ disebut nilai eigen atau nilai eigen dari operator A, yang bersesuaian dengan vektor eigen.
Mari kita perhatikan beberapa sifat nilai eigen dan vektor eigen.
1. Setiap kombinasi linier dari vektor eigen operator A yang bersesuaian dengan nilai eigen yang sama λ adalah vektor eigen dengan nilai eigen yang sama.
2. Vektor eigen operator A dengan nilai eigen berbeda berpasangan λ 1 , λ 2 , …, λ m bebas linier.
3. Jika nilai eigen λ 1 =λ 2 = λ m = λ, maka nilai eigen λ berhubungan dengan tidak lebih dari m vektor eigen bebas linier.

Jadi, jika terdapat n vektor eigen bebas linier , sesuai dengan nilai eigen yang berbeda λ 1, λ 2, ..., λ n, maka nilai-nilai tersebut bebas linier, oleh karena itu, nilai-nilai tersebut dapat diambil sebagai basis ruang R n. Mari kita cari bentuk matriks dari operator linier A berdasarkan vektor eigennya, yang mana kita akan bertindak dengan operator A berdasarkan vektor basis: Kemudian .
Jadi, matriks operator linier A berdasarkan vektor eigennya berbentuk diagonal, dan nilai eigen operator A berada di sepanjang diagonal.
Apakah ada basis lain yang matriksnya berbentuk diagonal? Jawaban atas pertanyaan ini diberikan oleh teorema berikut.

Dalil. Matriks operator linier A pada basis (i = 1..n) berbentuk diagonal jika dan hanya jika semua vektor basisnya merupakan vektor eigen dari operator A.

Aturan untuk mencari nilai eigen dan vektor eigen

. (*)

(1)
Di mana - matriks operator linier.

Sistem (1) mempunyai solusi bukan nol jika determinannya D sama dengan nol

Contoh 12. Operator linier A bekerja di R 3 menurut hukum, dimana x 1, x 2, .., x n adalah koordinat vektor di basis , , . Temukan nilai eigen dan vektor eigen dari operator ini.
Larutan. Kami membangun matriks operator ini:
.
Kami membuat sistem untuk menentukan koordinat vektor eigen:

Kami membuat persamaan karakteristik dan menyelesaikannya:

.
λ 1,2 = -1, λ 3 = 3.
Substitusikan λ = -1 ke dalam sistem, kita peroleh:
atau
Karena , maka ada dua variabel terikat dan satu variabel bebas.
Misalkan x 1 adalah bilangan tak diketahui bebas Kita selesaikan sistem ini dengan cara apa pun dan temukan solusi umum dari sistem ini: Sistem solusi fundamental terdiri dari satu solusi, karena n - r = 3 - 2 = 1.
Himpunan vektor eigen yang bersesuaian dengan nilai eigen λ = -1 berbentuk: , dengan x 1 adalah bilangan apa pun selain nol. Mari kita pilih satu vektor dari himpunan ini, misalnya dengan memasukkan x 1 = 1: .
Dengan alasan yang sama, kita menemukan vektor eigen yang sesuai dengan nilai eigen λ = 3: .
Dalam ruang R 3, basis terdiri dari tiga vektor bebas linier, tetapi kita hanya menerima dua vektor eigen bebas linier, yang darinya basis di R 3 tidak dapat dibuat. Akibatnya, kita tidak dapat mereduksi matriks A dari operator linier menjadi bentuk diagonal.

Contoh 13. Diberikan sebuah matriks .
1. Buktikan bahwa vektor adalah vektor eigen dari matriks A. Temukan nilai eigen yang sesuai dengan vektor eigen tersebut.
2. Temukan basis yang matriks A berbentuk diagonal.
Larutan.
1. Jika , maka merupakan vektor eigen

.
Vektor (1, 8, -1) merupakan vektor eigen. Nilai eigen λ = -1.
Matriks tersebut mempunyai bentuk diagonal dengan basis yang terdiri dari vektor-vektor eigen. Salah satunya terkenal. Mari kita temukan sisanya.
Kami mencari vektor eigen dari sistem:

Persamaan karakteristik: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Mari kita cari vektor eigen yang sesuai dengan nilai eigen λ = -3:

Pangkat matriks sistem ini adalah dua dan sama dengan banyaknya yang tidak diketahui, jadi sistem ini hanya mempunyai solusi nol x 1 = x 3 = 0. x 2 di sini bisa berupa apa pun selain nol, misalnya x 2 = 1. Jadi, vektor (0 ,1,0) adalah vektor eigen yang bersesuaian dengan λ = -3. Mari kita periksa:
.
Jika λ = 1, maka diperoleh sistemnya
Pangkat matriksnya adalah dua. Kami mencoret persamaan terakhir.
Misalkan x 3 adalah suatu bilangan tidak diketahui bebas. Maka x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Dengan asumsi x 3 = 1, kita mempunyai (-3,-9,1) - vektor eigen yang sesuai dengan nilai eigen λ = 1. Periksa:

.
Karena nilai eigennya nyata dan berbeda, maka vektor-vektor yang bersesuaian dengannya adalah bebas linier, sehingga dapat dijadikan basis dalam R 3 . Jadi, sebagai dasarnya , , matriks A berbentuk:
.
Tidak semua matriks operator linier A:R n → R n dapat direduksi menjadi bentuk diagonal, karena untuk beberapa operator linier mungkin terdapat kurang dari n vektor eigen bebas linier. Namun, jika matriksnya simetris, maka akar persamaan karakteristik multiplisitas m bersesuaian dengan tepat m vektor bebas linier.

Definisi. Matriks simetris adalah matriks persegi yang elemen-elemennya simetris terhadap diagonal utamanya adalah sama, yaitu .
Catatan. 1. Semua nilai eigen matriks simetris adalah nyata.
2. Vektor eigen suatu matriks simetris yang bersesuaian dengan nilai eigen berbeda berpasangan adalah ortogonal.
Sebagai salah satu dari banyak aplikasi peralatan yang dipelajari, kami mempertimbangkan masalah penentuan jenis kurva orde kedua.

Vektor eigen suatu matriks persegi adalah vektor yang jika dikalikan dengan matriks tertentu akan menghasilkan vektor yang kolinear. Dengan kata sederhana, ketika suatu matriks dikalikan dengan vektor eigen, vektor eigen tetap sama, tetapi dikalikan dengan bilangan tertentu.

Definisi

Vektor eigen adalah vektor bukan nol V, yang bila dikalikan dengan matriks persegi M, akan bertambah sejumlah λ. Dalam notasi aljabar terlihat seperti:

M × V = λ × V,

dimana λ adalah nilai eigen dari matriks M.

Mari kita lihat contoh numerik. Untuk memudahkan pencatatan, bilangan-bilangan pada matriks akan dipisahkan dengan titik koma. Mari kita punya matriks:

• M = 0; 4;
• 6; 10.

Mari kalikan dengan vektor kolom:

• V = -2;

Saat kita mengalikan matriks dengan vektor kolom, kita juga mendapatkan vektor kolom. Dalam bahasa matematika yang ketat, rumus mengalikan matriks 2 × 2 dengan vektor kolom akan terlihat seperti ini:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 berarti elemen matriks M yang terletak pada baris pertama dan kolom pertama, dan M22 berarti elemen yang terletak pada baris kedua dan kolom kedua. Untuk matriks kita, elemen-elemen tersebut sama dengan M11 = 0, M12 = 4, M21 = 6, M22 10. Untuk vektor kolom, nilainya sama dengan V11 = –2, V21 = 1. Menurut rumus ini, kita memperoleh hasil perkalian matriks persegi dengan vektor sebagai berikut:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Untuk memudahkan, mari kita tulis vektor kolom menjadi satu baris. Jadi, kita mengalikan matriks persegi dengan vektor (-2; 1), menghasilkan vektor (4; -2). Jelasnya, ini adalah vektor yang sama dikalikan dengan λ = -2. Lambda dalam hal ini menunjukkan nilai eigen dari matriks.

Vektor eigen suatu matriks adalah vektor kolinear, yaitu suatu benda yang tidak berubah posisinya dalam ruang jika dikalikan dengan suatu matriks. Konsep kolinearitas dalam aljabar vektor mirip dengan istilah paralelisme dalam geometri. Dalam interpretasi geometris, vektor-vektor collinear adalah segmen-segmen berarah paralel dengan panjang berbeda. Sejak zaman Euclid, kita mengetahui bahwa satu garis memiliki jumlah garis sejajar yang tak terhingga, sehingga masuk akal untuk mengasumsikan bahwa setiap matriks memiliki jumlah vektor eigen yang tak terhingga.

Dari contoh sebelumnya terlihat jelas bahwa vektor eigen dapat berupa (-8; 4), dan (16; -8), dan (32, -16). Ini semua adalah vektor kolinear yang sesuai dengan nilai eigen λ = -2. Saat mengalikan matriks asli dengan vektor-vektor ini, kita akan tetap mendapatkan vektor yang berbeda dari aslinya sebanyak 2 kali. Oleh karena itu, ketika menyelesaikan masalah pencarian vektor eigen, yang perlu dicari hanyalah objek vektor bebas linier. Seringkali, untuk matriks berukuran n × n, terdapat sejumlah n vektor eigen. Kalkulator kami dirancang untuk analisis matriks persegi orde kedua, sehingga hampir selalu hasilnya akan menemukan dua vektor eigen, kecuali jika keduanya bertepatan.

Pada contoh di atas, kita mengetahui vektor eigen matriks asli terlebih dahulu dan menentukan bilangan lambda dengan jelas. Namun, dalam praktiknya, yang terjadi sebaliknya: nilai eigen ditemukan terlebih dahulu, baru kemudian vektor eigen.

Algoritma solusi

Mari kita lihat kembali matriks asli M dan coba cari kedua vektor eigennya. Jadi matriksnya terlihat seperti:

• M = 0; 4;
• 6; 10.

Pertama kita perlu menentukan nilai eigen λ, yang memerlukan penghitungan determinan matriks berikut:

• (0 − λ); 4;
• 6; (10 −λ).

Matriks ini diperoleh dengan mengurangkan λ yang tidak diketahui dari elemen-elemen pada diagonal utama. Penentunya ditentukan dengan menggunakan rumus standar:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Karena vektor kita harus bukan nol, kita menerima persamaan yang dihasilkan sebagai persamaan bergantung linier dan menyamakan determinan detA kita dengan nol.

(0 − λ) × (10 − λ) − 24 = 0

Mari kita buka tanda kurung dan dapatkan persamaan karakteristik matriksnya:

λ 2 − 10λ − 24 = 0

Ini adalah persamaan kuadrat standar yang perlu diselesaikan dengan menggunakan diskriminan.

D = b 2 − 4ac = (-10) × 2 − 4 × (-1) × 24 = 100 + 96 = 196

Akar diskriminannya adalah akar kuadrat(D) = 14, maka λ1 = -2, λ2 = 12. Sekarang untuk setiap nilai lambda kita perlu mencari vektor eigennya. Mari kita nyatakan koefisien sistem untuk λ = -2.

• M − λ × E = 2; 4;
• 6; 12.

Dalam rumus ini, E adalah matriks identitas. Berdasarkan matriks yang dihasilkan, kami membuat sistem persamaan linier:

2x + 4y = 6x + 12y,

dimana x dan y adalah elemen vektor eigen.

Mari kita kumpulkan semua tanda X di sebelah kiri dan semua tanda Y di sebelah kanan. Jelasnya - 4x = 8y. Bagilah ekspresi tersebut dengan - 4 dan dapatkan x = –2y. Sekarang kita dapat menentukan vektor eigen pertama dari matriks tersebut, dengan mengambil nilai apa pun yang tidak diketahui (ingat tak terhingga dari vektor eigen yang bergantung linier). Misalkan y = 1, maka x = –2. Oleh karena itu, vektor eigen pertama terlihat seperti V1 = (–2; 1). Kembali ke awal artikel. Objek vektor inilah yang kami kalikan matriksnya untuk mendemonstrasikan konsep vektor eigen.

Sekarang mari kita cari vektor eigen untuk λ = 12.

• M - λ × E = -12; 4
• 6; -2.

Mari kita buat sistem persamaan linear yang sama;

• -12x + 4y = 6x − 2y
• -18x = -6 tahun
• 3x = kamu.

Sekarang kita ambil x = 1, maka y = 3. Jadi, vektor eigen kedua terlihat seperti V2 = (1; 3). Saat mengalikan matriks asli dengan vektor tertentu, hasilnya akan selalu berupa vektor yang sama dikalikan 12. Di sinilah algoritma penyelesaian berakhir. Sekarang Anda tahu cara menentukan vektor eigen suatu matriks secara manual.

• penentu;
• jejak, yaitu jumlah elemen-elemen pada diagonal utama;
• rangking, yaitu jumlah maksimum baris/kolom yang bebas linier.

Program ini beroperasi sesuai dengan algoritma di atas, mempersingkat proses solusi sebanyak mungkin. Penting untuk diperhatikan bahwa dalam program lambda ditandai dengan huruf “c”. Mari kita lihat contoh numerik.

Contoh cara kerja program

Mari kita coba menentukan vektor eigen untuk matriks berikut:

• M = 5; 13;
• 4; 14.

Mari masukkan nilai-nilai ini ke dalam sel kalkulator dan dapatkan jawabannya dalam bentuk berikut:

• Peringkat matriks: 2;
• Penentu matriks: 18;
• Jejak matriks: 19;
• Perhitungan vektor eigen: c 2 − 19.00c + 18.00 (persamaan karakteristik);
• Perhitungan vektor eigen: 18 (nilai lambda pertama);
• Perhitungan vektor eigen: 1 (nilai lambda kedua);
• Sistem persamaan vektor 1: -13x1 + 13y1 = 4x1 − 4y1;
• Sistem persamaan vektor 2: 4x1 + 13y1 = 4x1 + 13y1;
• Vektor eigen 1: (1; 1);
• Vektor eigen 2 : (-3.25; 1).

Jadi, kami memperoleh dua vektor eigen yang bebas linier.

Kesimpulan

Aljabar linier dan geometri analitik adalah mata pelajaran standar untuk setiap mahasiswa teknik baru. Banyaknya vektor dan matriks sangat menakutkan, dan mudah sekali terjadi kesalahan dalam perhitungan yang rumit tersebut. Program kami akan memungkinkan siswa untuk memeriksa perhitungan mereka atau secara otomatis memecahkan masalah pencarian vektor eigen. Ada kalkulator aljabar linier lainnya di katalog kami; gunakanlah dalam studi atau pekerjaan Anda.

www.situs memungkinkan Anda menemukan. Situs melakukan perhitungan. Dalam beberapa detik server akan memberikan solusi yang tepat. Persamaan karakteristik matriks akan menjadi ekspresi aljabar yang ditemukan menggunakan aturan untuk menghitung determinan matriks matriks, sedangkan sepanjang diagonal utama akan terdapat perbedaan nilai elemen diagonal dan variabelnya. Saat menghitung persamaan karakteristik untuk matriks online, setiap elemen matriks akan dikalikan dengan elemen lain yang bersesuaian matriks. Temukan dalam mode on line hanya mungkin untuk persegi matriks. Menemukan operasi persamaan karakteristik untuk matriks online direduksi menjadi menghitung jumlah aljabar hasil kali unsur-unsur matriks sebagai hasil menemukan determinannya matriks, hanya untuk tujuan menentukan persamaan karakteristik untuk matriks online. Operasi ini menempati tempat khusus dalam teori matriks, memungkinkan Anda menemukan nilai eigen dan vektor menggunakan akar. Tugas menemukan persamaan karakteristik untuk matriks online terdiri dari perkalian elemen matriks dilanjutkan dengan menjumlahkan hasil kali tersebut menurut aturan tertentu. www.situs menemukan persamaan karakteristik matriks dimensi tertentu dalam mode on line. Perhitungan persamaan karakteristik untuk matriks online mengingat dimensinya, ini adalah mencari polinomial dengan koefisien numerik atau simbolik, yang ditemukan menurut aturan untuk menghitung determinan matriks- sebagai jumlah produk dari elemen-elemen yang bersesuaian matriks, hanya untuk tujuan menentukan persamaan karakteristik untuk matriks online. Menemukan polinomial terhadap variabel untuk kuadrat matriks, sebagai definisi persamaan karakteristik matriks, umum dalam teori matriks. Arti dari akar-akar polinomial persamaan karakteristik untuk matriks online digunakan untuk menentukan vektor eigen dan nilai eigen untuk matriks. Apalagi jika determinannya matriks akan sama dengan nol, maka persamaan karakteristik matriks akan tetap ada, tidak seperti sebaliknya matriks. Untuk menghitung persamaan karakteristik matriks atau temukan beberapa sekaligus persamaan karakteristik matriks, Anda perlu menghabiskan banyak waktu dan tenaga, sementara server kami akan menemukannya dalam hitungan detik persamaan karakteristik matriks online. Dalam hal ini, jawabannya adalah temuan persamaan karakteristik untuk matriks online akan benar dan dengan akurasi yang cukup, bahkan jika angkanya ditemukan persamaan karakteristik untuk matriks online akan menjadi tidak rasional. Di tempat www.situs entri karakter diperbolehkan dalam elemen matriks, itu adalah persamaan karakteristik matriks online dapat direpresentasikan dalam bentuk simbolik umum saat menghitung persamaan karakteristik matriks online. Berguna untuk memeriksa jawaban yang diperoleh ketika memecahkan masalah penemuan persamaan karakteristik untuk matriks online menggunakan situs www.situs. Saat melakukan operasi penghitungan polinomial - persamaan karakteristik matriks, Anda harus berhati-hati dan sangat fokus saat menyelesaikan masalah ini. Pada gilirannya, situs kami akan membantu Anda memeriksa keputusan Anda mengenai topik tersebut persamaan karakteristik matriks online. Jika Anda tidak punya waktu untuk memeriksa masalah yang terpecahkan dalam waktu lama, maka www.situs tentu akan menjadi alat yang berguna untuk memeriksa saat mencari dan menghitung persamaan karakteristik untuk matriks online.

SISTEM PERSAMAAN LINEAR HOMOGEN

Sistem persamaan linier homogen adalah sistem yang bentuknya

Jelas sekali dalam kasus ini , Karena semua elemen salah satu kolom pada determinan ini sama dengan nol.

Karena yang tidak diketahui ditemukan menurut rumus , maka jika Δ ≠ 0, sistem mempunyai solusi nol yang unik X = kamu = z= 0. Namun, dalam banyak soal, pertanyaan yang menarik adalah apakah sistem homogen mempunyai solusi selain nol.

Dalil. Agar suatu sistem persamaan linier homogen memiliki solusi bukan nol, maka perlu dan cukup bahwa Δ ≠ 0.

Jadi, jika determinannya Δ ≠ 0, maka sistem tersebut mempunyai solusi unik. Jika Δ ≠ 0, maka sistem persamaan linier homogen mempunyai jumlah penyelesaian yang tak terhingga.

Contoh.

Vektor eigen dan nilai eigen suatu matriks

Biarkan matriks persegi diberikan , X– beberapa kolom matriks yang tingginya bertepatan dengan orde matriks A. .

Dalam banyak soal kita harus mempertimbangkan persamaannya X

dimana λ adalah bilangan tertentu. Jelas bahwa untuk setiap λ persamaan ini mempunyai solusi nol.

Bilangan λ yang persamaannya mempunyai penyelesaian bukan nol disebut nilai eigen matriks A, A X karena λ seperti itu disebut vektor eigen matriks A.

Mari kita cari vektor eigen matriks tersebut A. Karena E∙X = X, maka persamaan matriksnya dapat ditulis ulang menjadi atau . Dalam bentuk yang diperluas, persamaan ini dapat ditulis ulang sebagai sistem persamaan linier. Benar-benar .

Dan maka dari itu

Jadi, kita telah memperoleh sistem persamaan linier homogen untuk menentukan koordinat x 1, x 2, x 3 vektor X. Agar suatu sistem mempunyai solusi bukan nol, maka determinan sistem tersebut harus sama dengan nol, yaitu.

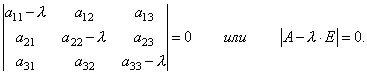
Ini adalah persamaan derajat ke-3 untuk λ. Ini disebut persamaan karakteristik matriks A dan berfungsi untuk menentukan nilai eigen dari λ.

Setiap nilai eigen λ berhubungan dengan vektor eigen X, yang koordinatnya ditentukan dari sistem pada nilai λ yang sesuai.

Contoh.

ALJABAR VEKTOR. KONSEP VEKTOR

Dalam mempelajari berbagai cabang ilmu fisika, ada besaran yang ditentukan sepenuhnya dengan menentukan nilai numeriknya, misalnya panjang, luas, massa, suhu, dll. Besaran seperti ini disebut skalar. Namun selain besaran juga ada besaran yang untuk menentukannya selain nilai numerik juga perlu diketahui arahnya dalam ruang, misalnya gaya yang bekerja pada benda, kecepatan dan percepatan benda. suatu benda ketika bergerak di ruang angkasa, kekuatan medan magnet pada suatu titik tertentu di ruang angkasa, dan sebagainya. Besaran seperti ini disebut besaran vektor.

Mari kita perkenalkan definisi yang ketat.

Segmen yang diarahkan Sebut saja suatu ruas yang ujung-ujungnya diketahui mana yang pertama dan mana yang kedua.

Vektor disebut segmen berarah yang mempunyai panjang tertentu, yaitu Ini adalah segmen dengan panjang tertentu, di mana salah satu titik yang membatasinya diambil sebagai awal, dan titik kedua sebagai akhir. Jika A– awal vektor, B adalah ujungnya, maka vektor dilambangkan dengan simbol; selain itu, vektor sering dilambangkan dengan satu huruf. Pada gambar, vektor ditunjukkan dengan segmen, dan arahnya ditunjukkan dengan panah.

Modul atau panjang Vektor disebut panjang segmen berarah yang mendefinisikannya. Dilambangkan dengan || atau ||.

Kami juga akan memasukkan apa yang disebut vektor nol, yang awal dan akhirnya bertepatan, sebagai vektor. Itu ditunjuk. Vektor nol tidak memiliki arah tertentu dan modulusnya nol ||=0.

Vektor disebut segaris, jika letaknya pada garis yang sama atau pada garis sejajar. Apalagi jika vektor-vektornya dan searah, kita tuliskan , berlawanan.

Vektor yang terletak pada garis lurus yang sejajar pada bidang yang sama disebut sebidang.

Kedua vektor tersebut disebut setara, jika keduanya segaris, searah, dan panjangnya sama. Dalam hal ini mereka menulis.

Dari definisi persamaan vektor dapat disimpulkan bahwa suatu vektor dapat dipindahkan sejajar dengan dirinya sendiri, menempatkan titik asal pada titik mana pun dalam ruang.

Misalnya.

OPERASI LINEAR PADA VEKTOR

1. Mengalikan vektor dengan angka.

   Hasil kali suatu vektor dan bilangan λ merupakan suatu vektor baru sehingga:

   Hasil kali vektor dan bilangan λ dilambangkan dengan .

   

   Misalnya, ada sebuah vektor yang arahnya sama dengan vektor tersebut dan panjangnya setengah dari vektor tersebut.

   Operasi yang diperkenalkan memiliki yang berikut ini properti:

2. Penambahan vektor.

   Misalkan dan menjadi dua vektor sembarang. Mari kita ambil sudut pandang yang sewenang-wenang HAI dan membuat vektor. Setelah itu dari intinya A mari kita kesampingkan vektornya. Vektor yang menghubungkan awal vektor pertama dengan akhir vektor kedua disebut jumlah dari vektor-vektor ini dan dilambangkan .

   

   Definisi penjumlahan vektor yang dirumuskan disebut aturan jajaran genjang, karena jumlah vektor yang sama dapat diperoleh sebagai berikut. Mari kita tunda dari intinya HAI vektor dan . Mari kita membuat jajar genjang pada vektor-vektor ini OABC. Karena vektor, maka vektor, yaitu diagonal jajar genjang yang ditarik dari titik sudutnya HAI, jelas merupakan jumlah dari vektor.

   

   Caranya mudah untuk memeriksa hal berikut ini sifat penjumlahan vektor.

3. Perbedaan vektor.

   Suatu vektor yang segaris terhadap suatu vektor tertentu, sama panjang dan berlawanan arah, disebut di depan vektor untuk suatu vektor dan dilambangkan dengan . Vektor yang berlawanan dapat dianggap sebagai hasil perkalian vektor dengan bilangan λ = –1: .

Dengan matriks A, jika terdapat bilangan l sehingga AX = lX.

Dalam hal ini, nomor l dipanggil nilai eigen operator (matriks A) yang bersesuaian dengan vektor X.

Dengan kata lain, vektor eigen adalah vektor yang, di bawah aksi operator linier, berubah menjadi vektor kolinear, yaitu. kalikan saja dengan angka tertentu. Sebaliknya, vektor tak wajar lebih rumit untuk diubah.

Mari kita tuliskan definisi vektor eigen dalam bentuk sistem persamaan:

Mari kita pindahkan semua suku ke sisi kiri:

Sistem yang terakhir dapat ditulis dalam bentuk matriks sebagai berikut:

(A - lE)X = O

Sistem yang dihasilkan selalu mempunyai solusi nol X = O. Sistem yang semua suku bebasnya sama dengan nol disebut homogen. Jika matriks sistem tersebut berbentuk persegi dan determinannya tidak sama dengan nol, maka dengan menggunakan rumus Cramer kita akan selalu mendapatkan solusi unik - nol. Dapat dibuktikan bahwa suatu sistem mempunyai solusi bukan nol jika dan hanya jika determinan matriks tersebut sama dengan nol, yaitu.

|A - le| = = 0

Persamaan dengan l yang tidak diketahui ini disebut persamaan karakteristik (polinomial karakteristik) matriks A (operator linier).

Dapat dibuktikan bahwa polinomial karakteristik suatu operator linier tidak bergantung pada pilihan basis.

Misalnya, cari nilai eigen dan vektor eigen dari operator linier yang ditentukan oleh matriks A = .

Untuk melakukannya, mari kita buat persamaan karakteristik |A - lE| = = (1 - l) 2 - 36 = 1 - 2l + l 2 - 36 = l 2 - 2l - 35 = 0; D = 4 + 140 = 144; nilai eigen l 1 = (2 - 12)/2 = -5; aku 2 = (2 + 12)/2 = 7.

Untuk mencari vektor eigen, kita menyelesaikan dua sistem persamaan

(A + 5E)X = O

(A - 7E)X = O

Untuk yang pertama, matriks yang diperluas mengambil bentuk

,

maka x 2 = c, x 1 + (2/3)c = 0; x 1 = -(2/3)s, mis. X (1) = (-(2/3)s; s).

Untuk yang kedua, matriks yang diperluas mengambil bentuk

,

dari mana x 2 = c 1, x 1 - (2/3)c 1 = 0; x 1 = (2/3)s 1, yaitu X (2) = ((2/3) s 1; s 1).

Jadi, vektor eigen dari operator linier ini adalah semua vektor berbentuk (-(2/3)с; с) dengan nilai eigen (-5) dan semua vektor berbentuk ((2/3)с 1 ; с 1) dengan nilai eigen 7 .

Dapat dibuktikan bahwa matriks operator A pada basis yang terdiri dari vektor-vektor eigennya berbentuk diagonal dan berbentuk:

,

dimana aku adalah nilai eigen dari matriks ini.

Kebalikannya juga benar: jika matriks A pada suatu basis berbentuk diagonal, maka semua vektor pada basis tersebut akan menjadi vektor eigen dari matriks tersebut.

Dapat juga dibuktikan bahwa jika suatu operator linier mempunyai n nilai eigen berbeda berpasangan, maka vektor eigen yang bersesuaian adalah bebas linier, dan matriks operator ini pada basis yang bersesuaian berbentuk diagonal.

Mari kita ilustrasikan hal ini dengan contoh sebelumnya. Mari kita ambil nilai sembarang bukan nol c dan c 1, tetapi sedemikian rupa sehingga vektor X (1) dan X (2) bebas linier, mis. akan membentuk suatu dasar. Misal c = c 1 = 3, maka X (1) = (-2; 3), X (2) = (2; 3).

Mari kita verifikasi independensi linier dari vektor-vektor ini:

12 ≠ 0. Pada basis baru ini, matriks A akan berbentuk A * = .

Untuk memverifikasinya, mari kita gunakan rumus A* = C -1 AC. Pertama, cari C -1.

C -1 = ;

Bentuk kuadrat

Bentuk kuadrat f(x 1, x 2, xn) dari n variabel disebut penjumlahan, yang setiap sukunya merupakan kuadrat salah satu variabel, atau hasil kali dua variabel berbeda, diambil dengan koefisien tertentu: f(x 1 , x 2, xn) = (a ij = aji).

Matriks A yang tersusun dari koefisien-koefisien ini disebut matriks bentuk kuadrat. Selalu simetris matriks (yaitu matriks yang simetris terhadap diagonal utama, a ij = a ji).

Dalam notasi matriks, bentuk kuadratnya adalah f(X) = X T AX, dimana

Memang

Misalnya kita menulis bentuk kuadrat dalam bentuk matriks.

Untuk melakukan ini, kita menemukan matriks berbentuk kuadrat. Elemen diagonalnya sama dengan koefisien variabel kuadrat, dan elemen sisanya sama dengan setengah koefisien bentuk kuadrat yang bersesuaian. Itu sebabnya

Misalkan kolom-matriks variabel X diperoleh dengan transformasi linier tak-degenerasi dari kolom-matriks Y, yaitu. X = CY, dimana C adalah matriks nonsingular orde ke-n. Maka bentuk kuadratnya f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Jadi, dengan transformasi linier tak berdegenerasi C, matriks berbentuk kuadrat berbentuk: A* = C T AC.

Misalnya, cari bentuk kuadrat f(y 1, y 2), yang diperoleh dari bentuk kuadrat f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 melalui transformasi linier.

Bentuk kuadrat disebut resmi(Memiliki pandangan kanonik), jika semua koefisiennya a ij = 0 untuk i ≠ j, yaitu
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 = .

Matriksnya berbentuk diagonal.

Dalil(bukti tidak diberikan di sini). Bentuk kuadrat apa pun dapat direduksi menjadi bentuk kanonik menggunakan transformasi linier tak merosot.

Misalnya, mari kita reduksi bentuk kuadrat menjadi bentuk kanonik
f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

Untuk melakukan ini, pertama-tama pilih persegi lengkap dengan variabel x 1:

f(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 = 2(x 1 + x 2) 2 - 5x 2 2 - x 2 x 3.

Sekarang kita pilih persegi lengkap dengan variabel x 2:

f(x 1, x 2, x 3) = 2(x 1 + x 2) 2 - 5(x 2 2 + 2* x 2 *(1/10)x 3 + (1/100)x 3 2) + (5/100)x 3 2 =
= 2(x 1 + x 2) 2 - 5(x 2 - (1/10)x 3) 2 + (1/20)x 3 2.

Kemudian transformasi linier tak berdegenerasi y 1 = x 1 + x 2, y 2 = x 2 + (1/10)x 3 dan y 3 = x 3 menjadikan bentuk kuadrat ini menjadi bentuk kanonik f(y 1, y 2 , kamu 3) = 2kamu 1 2 - 5kamu 2 2 + (1/20)kamu 3 2 .

Perhatikan bahwa bentuk kanonik dari bentuk kuadrat ditentukan secara ambigu (bentuk kuadrat yang sama dapat direduksi menjadi bentuk kanonik dengan cara yang berbeda). Namun, bentuk kanonik yang diperoleh dengan berbagai metode memiliki sejumlah sifat yang sama. Secara khusus, jumlah suku dengan koefisien positif (negatif) dari bentuk kuadrat tidak bergantung pada metode pengurangan bentuk menjadi bentuk ini (misalnya, dalam contoh yang dipertimbangkan akan selalu ada dua koefisien negatif dan satu positif). Sifat ini disebut hukum inersia bentuk kuadrat.

Mari kita verifikasi ini dengan membawa bentuk kuadrat yang sama ke bentuk kanoniknya dengan cara yang berbeda. Mari kita mulai transformasi dengan variabel x 2:

f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3(x 2 2 +
+ 2* x 2 ((1/6) x 3 - (2/3)x 1) + ((1/6) x 3 - (2/3)x 1) 2) + 3((1/6) x 3 - (2/3)x 1) 2 + 2x 1 2 =
= -3(x 2 + (1/6) x 3 - (2/3)x 1) 2 + 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 = f (kamu 1 , kamu 2 , kamu 3) = -3kamu 1 2 -
+3y 2 2 + 2y 3 2, dimana y 1 = - (2/3)x 1 + x 2 + (1/6) x 3, y 2 = (2/3)x 1 + (1/6) x 3 dan kamu 3 = x 1 . Di sini terdapat koefisien negatif -3 pada y 1 dan dua koefisien positif 3 dan 2 pada y 2 dan y 3 (dan dengan menggunakan metode lain kita mendapatkan koefisien negatif (-5) pada y 2 dan dua koefisien positif: 2 pada y 1 dan 1/20 pada y 3).

Perlu juga diperhatikan bahwa pangkat suatu matriks berbentuk kuadrat disebut peringkat bentuk kuadrat, sama dengan jumlah koefisien bukan nol dalam bentuk kanonik dan tidak berubah pada transformasi linier.

Bentuk kuadrat f(X) disebut secara positif (negatif) yakin, jika untuk semua nilai variabel yang tidak simultan sama dengan nol, bernilai positif, yaitu f(X) > 0 (negatif, mis.
f(x)< 0).

Misalnya bentuk kuadrat f 1 (X) = x 1 2 + x 2 2 adalah pasti positif, karena adalah jumlah kuadrat, dan bentuk kuadrat f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 adalah pasti negatif, karena menyatakannya dapat direpresentasikan sebagai f 2 (X) = -(x 1 - x 2) 2.

Dalam sebagian besar situasi praktis, agak lebih sulit untuk menetapkan tanda pasti suatu bentuk kuadrat, jadi untuk ini kami menggunakan salah satu teorema berikut (kami akan merumuskannya tanpa bukti).

Dalil. Suatu bentuk kuadrat pasti positif (negatif) jika dan hanya jika semua nilai eigen matriksnya positif (negatif).

Dalil(Kriteria Sylvester). Suatu bentuk kuadrat adalah pasti positif jika dan hanya jika semua minor utama dari matriks bentuk ini adalah positif.

Utama (sudut) minor Matriks A orde ke-k dari orde ke-n disebut determinan matriks, terdiri dari k baris dan kolom pertama matriks A().

Perhatikan bahwa untuk bentuk kuadrat pasti negatif, tanda minor utama bergantian, dan minor orde pertama harus negatif.

Sebagai contoh, mari kita periksa bentuk kuadrat f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 untuk mengetahui kepastian tanda.

= (2 - aku)*
*(3 - l) - 4 = (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 = 0; D = 25 - 8 = 17;
. Oleh karena itu, bentuk kuadratnya adalah pasti positif.

Cara 2. Minor utama matriks orde pertama A D 1 = a 11 = 2 > 0. Minor utama matriks orde kedua D 2 = = 6 - 4 = 2 > 0. Oleh karena itu, menurut kriteria Sylvester, bentuk kuadratnya adalah pasti positif.

Kita periksa bentuk kuadrat lain untuk kepastian tanda, f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Metode 1. Mari kita buat matriks berbentuk kuadrat A = . Persamaan karakteristiknya akan berbentuk = (-2 - aku)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Oleh karena itu, bentuk kuadratnya adalah pasti negatif.

Metode 2. Minor utama matriks orde pertama A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Oleh karena itu, menurut kriteria Sylvester, bentuk kuadratnya adalah pasti negatif (tanda-tanda minor utama bergantian, dimulai dengan minus).

Dan sebagai contoh lain, kita periksa bentuk kuadrat bertanda f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2.

Metode 1. Mari kita buat matriks berbentuk kuadrat A = . Persamaan karakteristiknya akan berbentuk = (2 - aku)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

Salah satu dari angka-angka ini negatif dan yang lainnya positif. Tanda nilai eigennya berbeda-beda. Oleh karena itu, bentuk kuadrat tidak dapat berdefinisi negatif maupun positif, yaitu. bentuk kuadrat ini tidak pasti tanda (dapat mengambil nilai tanda apa pun).

Cara 2. Minor utama matriks orde pertama A D 1 = a 11 = 2 > 0. Minor utama matriks orde kedua D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).