Това, което се нарича векторна диаграма на верига. Построяване на векторни диаграми на токове и напрежения. г) Векторни диаграми при наличие на трансформация
Разклонителните токове се намират веднага:
За да се определи общият ток, е необходимо да се изгради векторна диаграма (фиг. 23.1, b). Започваме конструкцията с вектора на напрежението, тъй като той е общ за всички клонове. От векторната диаграма имаме:
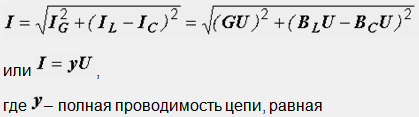
Разликата между индуктивната и капацитивната проводимост представлява общата реактивна проводимост на веригата B=B L -B C .
За да намерим средната мощност, консумирана от тази верига, трябва да вземем средното време от функцията. Напрежението в кондензатора изостава от тока. Поради фазовата разлика е полезно да се въведат фазори за описание на тези вериги. Обяснете предимствата на използването на векторното представяне.
В този и следващите Atoms ще обобщим закона на Ом, така че да можем да го използваме дори когато във веригата има кондензатори и индуктори. За да стигнем до там, първо ще представим много общ, картинен начин за представяне на синусоида с помощта на вектор.
Основната идея във фазовото представяне е, че сложен, променящ се във времето сигнал може да бъде представен като произведение на комплексно число и комплексен сигнал. Това може да бъде особено полезно, тъй като честотният фактор често е общ за всички компоненти на линейна комбинация от синусоиди.
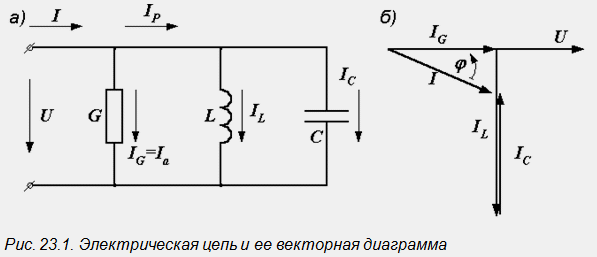
Векторите на тока в диаграмата образуват токов триъгълник. Неговият хоризонтален крак, представляващ проекцията на вектора на тока върху вектора на напрежението, се нарича активен компонент на тока и е равен на тока в активния елемент на веригата: I a =I g =GU (фиг. 23.2, а). Проекцията на вектора на тока върху посоката, перпендикулярна на напрежението, е реактивният компонент на тока. Той е равен на общия ток на реактивните елементи:
Ориз. 3: Фазорът може да се разглежда като вектор, въртящ се около началото в комплексната равнина. Функцията косинус е проекцията на вектор върху реалната ос. Това означава, че токът и напрежението ще достигнат връх едновременно. Казваме, че токът и напрежението са във фаза. Когато кондензаторът е свързан към AC напрежение, максималното напрежение е пропорционално на максималния ток, но максималното напрежение не възниква едновременно с максималния ток. Токът има максимална четвърт цикъл преди пикове на напрежението.

Разделяйки всички страни на текущия триъгълник с U, получаваме триъгълник на проводимост (фиг. 23.2, b), чиито страни са свързани със следните отношения:
2. Символен метод.
Преди това бяха получени следните формули:
Замествайки ги в уравнението на първия закон на Кирхоф, получаваме:
Г) Векторни диаграми при наличие на трансформация
Инженерите казват, че "токът води до напрежение с 90°." Ориз. 2: Токът достига четвърт вълна преди напрежението, когато кондензаторът е свързан към AC напрежение. Тъй като все още е напрежение, разделено на ток, неговата единица е ом. Кондензаторът влияе на тока, като има способността да го спира напълно, когато е напълно зареден.
Лицето за индуктора показва, че напрежението задвижва тока с 90º. . Разумно е да се приеме, че съпротивлението е пренебрежимо малко, защото на практика можем да направим съпротивлението на индуктора толкова малко, че да има малък ефект върху веригата. Графиката показва напрежението и тока като функция на времето. започва с максимално напрежение. Обърнете внимание, че токът започва от нула и след това се повишава до своя връх след напрежението, което го задвижва.
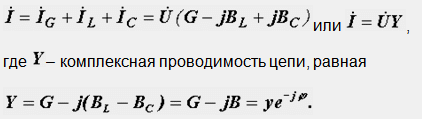
№24 Пасивна двуизводна мрежа във верига синусоидален ток. Еквивалентно съпротивление и проводимост.
На фиг. Фигура 24.1 показва пасивна двутерминална мрежа, състояща се от активни и реактивни елементи. Известни са ефективните стойности на напрежението U, тока I и фазовия ъгъл между тях φ.
След това токът става отрицателен, отново след напрежението. Следователно, когато се приложи синусоидално напрежение към индуктор, напрежението насочва тока през една четвърт цикъл или през ъгъл от 90º. Токът изостава от напрежението, тъй като индукторите се противопоставят на промяната в тока. Промяната в тока причинява ЕДС.
Напрежението през индуктора "провежда" ток поради закона на Ленц. Следователно, векторът, представляващ ток и напрежение, ще бъде даден като. Сравнете резонансните характеристики на вериги с по-високо и по-ниско съпротивление. Резонансът е склонността на една система да вибрира с по-голяма амплитуда при някои честоти, отколкото при други. Честотите, при които амплитудата на реакцията е относително максимална, са известни като резонансни честоти на системата.
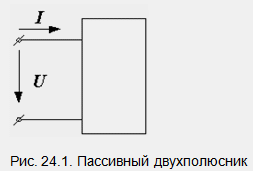
Нека да изградим векторна диаграма, използвайки тези стойности и, проектирайки вектора на напрежението върху текущия вектор и посоката, перпендикулярна на него, получаваме триъгълник на напрежението, образуван от страните U a, U p, U (фиг. 24.2 a).
Веригата се нарича последователна еквивалентна верига или последователна еквивалентна верига на пасивна двуизводна мрежа, а нейните параметри R, X и Z са еквивалентните съпротивления на двуизводната мрежа.
Това е и естествената честота, при която веригата ще трепти, ако не се управлява от източник на напрежение. Две криви за две различни вериги, които се различават само по количеството съпротивление в тях. Пикът е по-нисък и по-широк за веригата с по-високо съпротивление. По този начин веригите с по-високо съпротивление не резонират толкова силно и няма да бъдат толкова селективни, като например в радиоприемника.
Например за фаза А
въпреки това средна мощностне е просто напрежение във времето, какъвто е случаят с чисто резистивните вериги. Това означава, че φ = 0º и че напрежението и токът са във фаза, както се очаква за резистори. Фактът, че напрежението и токът на източника не са във фаза, влияе върху мощността, подадена към веригата. Може да се покаже, че средната мощност е равна.
![]()
Триъгълник, образуван от страни R, X, Z и подобен на триъгълник на напрежение, е триъгълник на съпротивление
Сега нека разложим текущия вектор на два компонента Ia - активен, насочен по протежение на вектора на напрежението, и реактивен Ip, перпендикулярен на него (фиг. 24.3, а). Такава векторна диаграма съответства на паралелна еквивалентна схема на двутерминална мрежа (фиг. 24.3, b). Неговите параметри G, B и Y се наричат еквивалентни проводимости. Представяме токовете в елементи G и B като активни и реактивни компоненти на общия ток: Ia=GU, Ip=BU. От триъгълника на тока (фиг. 24.3, а) се получава триъгълник на проводимост.
Ред на чертане на диаграми
Индукторът и кондензаторът имат вход и изход на енергия, но не разсейват енергия от веригата. По-скоро те прехвърлят енергия напред и назад един към друг, като резисторът разсейва точните количества, които източникът на напрежение осигурява на веригата. Това не включва значително електромагнитно излъчване от индуктора и кондензатора.
Обяснения за работа
Моделът е подобен на колелото на автомобил, движещ се по гофриран път, както се вижда на фигурата. Правилно разположените шипове на пътя са подобни на източника на напрежение, който задвижва колелото нагоре и надолу. Амортисьорът е подобен на амортизацията на съпротивлението и ограничава амплитудата на вибрациите. Енергията в една система тече напред-назад между кинетичната и потенциална енергия, съхраняван в пружина за кола. Амплитудата на движение на колелата е максимална, ако се ударят удари върху пътя резонансна честота.
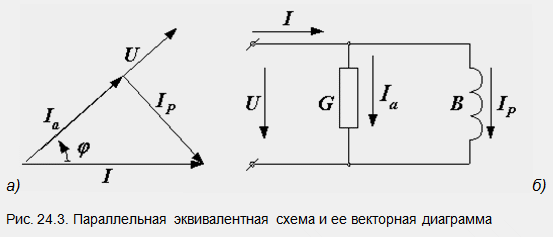
Нека получим условията за еквивалентност на дадените вериги.
За последователна верига U=IZ, за паралелна верига I=YU и тъй като токовете и напреженията в двете вериги са еднакви, тогава: Y=1/Z и Z=1/Y
тези. Във всяка електрическа верига общата проводимост е реципрочната на общото съпротивление.
Масата и пружината определят резонансната честота. Дължината на вектор представлява величина като тази. Колкото по-голяма е амплитудата на вълновата форма, толкова по-голяма е дължината на съответния вектор. Въпреки това, векторният ъгъл представлява фазовото изместване в градуси между въпросната форма на вълната и друга форма на вълната, действаща като "референтна" във времето. Обикновено, когато се изразява фазата на форма на вълната във верига, това се отнася до формата на вълната на захранващото напрежение. Не забравяйте, че фазата е винаги относително измерванемежду два режима на вибрация, а не като абсолютно свойство.
Формули за преход от серийна еквивалентна верига към паралелна:
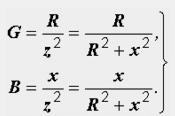
Формули за преход от паралелна еквивалентна верига към последователна:
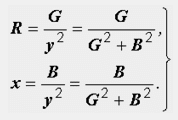
Моля, имайте предвид, че всяка от проводимостта G и B зависи от двете съпротивления - активно и реактивно. От своя страна всяко от съпротивленията се определя от двете проводимости. Съотношенията G = 1/R и B = 1/x са валидни само в специален случай, първото - за x = 0, второто - за R = 0.
Векторният ъгъл е фазата спрямо друга форма на вълната. Фазово отместване между вълни и векторен фазов ъгъл. Колкото по-голяма е разликата в градуса между два режима, толкова по-голяма е разликата в ъглите между съответните вектори. Тъй като е относително измерване като напрежението, фазовото изместване има смисъл само във връзка със стандартната форма на вълната.
Тази концепция за референтна точка не се различава много от концепцията за "заземяване" на верига в полза на референтно напрежение. От фазовата диаграма се проверява, че веригата е капацитивна, тъй като напрежението се забавя спрямо тока. Ако текущата нулева точка се вземе за начало, фазовата диаграма ще бъде показана на първата фигура. Ако той вземе източника на скритите времена, тогава фазовата диаграма ще бъде втората представена. Но и в двата случая фазовото изместване на текущото напрежение е същото, тъй като се налага от аргумента за натоварване. Приложената латентност и произтичащият ток са показани на фазовата диаграма на фигурата. Единствената обща променлива за всички елементи на пасивната верига е токът, протичащ през всички тях. Така определеното напрежение ще напредне под определен ъгъл, по-малък от 90° спрямо тока. Като вземем предвид всичко по-горе, ние конфигурираме шаблона на блендата на шаблона. Мотивите, дадени за неговото изграждане, са подобни на тези, дадени в предишен раздел. Токът ще бъде извън фаза под неизвестен ъгъл спрямо дихатацията, но тъй като това е индуктивна верига, тъй като се формира само от два резистора и една индуктивност, повредата ще се забави. Лицевата диаграма, съответстваща на веригата, е показана на придружаващата фигура. Следователно правилната конфигурация би била както в следната диаграма. Следователно ще бъде приложена верига, съответстваща на фазовата диаграма. Схематичната диаграма на веригата е показана на фигурата.
- Трябва да се отбележи, че и двете функции имат еднаква честота.
- Произходът на времената може да бъде променен.
Трябва да се отбележи, че активните и реактивните компоненти на напрежението и тока не съществуват физически и не могат да бъдат измерени. Те се отнасят само за съответните еквивалентни еквивалентни схеми и се намират чрез изчисление. Освен това, проектирайки например вектора на тока при различни напрежения, ще получим различни компоненти за него.
№25 Закон на Ом в символна форма за произволна верига.
Построяване на векторна диаграма на токовете
В този случай максималната стойност трябва да бъде разделена на корена от. Ъгълът представлява фазата. Скоростта на въртене ω е свързана с честотата на сигнала. В много случаи напреженията и токовете на вериги с променлив токса фазори един с друг. Във фазовите диаграми това се представя от ъгъла между векторите. В следващия пример има два сигнала на 90° във фаза, а отляво на двата вектора се виждат на 90 градуса един спрямо друг.
Те ще бъдат представени във фазовата диаграма, както следва. Подобно на комплексните числа, векторите могат да бъдат представени в биномна или полярна форма. В някои случаи ни е удобно да ги изразим, а в други случаи ще бъде по-лесно да обясним различна форма.
Нека моментните стойности на напрежението и тока на клемите на произволна пасивна двутерминална мрежа се определят от изразите, комплексите ефективни стойностикоито съответно са равни:
и тяхното съотношение определя комплексното съпротивление на двутерминалната мрежа:
Реципрочната стойност на комплексното съпротивление е комплексната проводимост:
В) Предназначение на векторните диаграми
Да предположим, че имаме следния израз за напрежение. Горният израз може да бъде представен като вектор, показващ максималното напрежение и ъгъла на изместване. В полярна форма предишното напрежение е представено от следващия вектор. Графично го виждаме по следния начин.
Като конвенция сигналите трябва да се изразяват с помощта на функцията косинус и с положителна стойностза извършване на фазов анализ. Ако не са изразени по този начин, трябва да ги конвертираме. Това е обяснено подробно в следващия раздел. Сигналът от предишния пример може да бъде изразен чрез неговите правоъгълни компоненти, като напр.
Съпротивленията z, R, x и проводимостта y, G и B, включени в последните два израза, не са нищо повече от еквивалентни параметри на двутерминална мрежа.
№26 За изчисляването на вериги със синусоидален ток.
Както следва от представения теоретичен материал и дадените примери, при анализа на вериги със синусоидален ток широко се използват векторни диаграми и комплексни числа. Самите векторни диаграми често служат за илюстриране на резултатите от теоретични изследвания и решаване на проблеми. Те помагат да се разбере по-добре същността на изучаваните процеси и да се визуализират връзките и връзките на напреженията и токовете на различни областис параметри на веригата.
Знания и умения за постигане
Графично имаме следната диаграма. Осигурете подходящи методологични и оперативни познания за изучаване на най-често срещаните електрически и индустриално оборудванесъс специално внимание на електромагнитните проблеми, което позволява на студентите да придобият критерии за избор и оптимизиране на работата. относно настройката на работната скорост.
Обща информация Препратки към законите на електромагнетизма и основните свойства на проводимите, диелектричните и феромагнитните материали, използвани в строителството електрически машини. в сравнение с диспергирани потоци Еквивалент електрическа схема, загуба на желязо, насищане на магнитната сърцевина Синусоида, фазова диаграма Работа на товара, номинална мощност и изход Промяна на напрежението с товари Празно и късо съединение, определяне на характерни параметри.
В много случаи векторните диаграми, предварително конструирани съгласно описаните по-горе правила без никакви изчисления, са основа за извличане от тях на специфична техника за решаване на даден проблем. Също така е възможно да се свърже векторна диаграма със сложни оси, да се изразят вектори с помощта на комплексни числа и допълнително да се изчисли в символна форма. Няма фундаментална разлика между метода на векторната диаграма и символния метод. Както видяхме по-рано, зад аналитичните операции с комплексни числа се крият определени геометрични операции с вектори.
Формули за изчисления
Паралелна работа, определение идеални условия. Трифазен трансформатор, магнитни вериги, вид на свързване на първични и вторична намоткапринадлежащи към групата. Симетрична и балансирана синусоидална работа. Анализ на ефективността на вакуума в различни случаи на първични и вторични връзки. Хармоници на тока и потока.
Определяне на хомополярен импеданс. Външни характеристики на трансформатор на омичен, индуктивен и капацитивен товар, промяна на напрежението от вакуум към товар, диаграма на Капа. Анализ на паралелна работа на трансформатори с различни коефициенти на трансформация.
Трябва също да се помни, че векторите и комплексните числа не носят никакво физическо съдържание. Това са чисто математически абстракции, необходими за анализ.
Символният метод се основава на законите на Ом и Кирхоф, които са записани в символна форма по същия начин, както в постоянните вериги. Следователно всички описани по-горе методи за изчисляване на вериги с постоянен ток, произтичащи от тези закони, са приложими и за изчисляване на вериги със синусоидален ток в символна форма.
№27 Явлението резонанс в електрически вериги.
Резонансът е режим, при който във верига, съдържаща индуктивност и капацитет, токът е във фаза с напрежението. Входното съпротивление и проводимост са нула: x = I m Z = 0 и B = I m Y = 0. Веригата е чисто активна: Z = R; няма фазово изместване (φ=0).
Напреженията в индуктивността и капацитета в този режим са равни по големина и, като са в противофаза, се компенсират взаимно. Цялото напрежение, приложено към веригата, пада върху нейното активно съпротивление (фиг. 27.1, а).
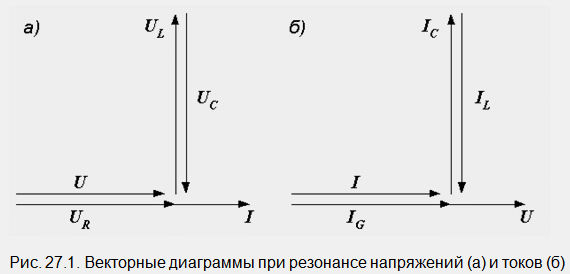
Напреженията на индуктивността и капацитета могат значително да надвишават напреженията на входа на веригата. Тяхното съотношение, наречено качествен фактор на веригата Q, се определя от стойностите на индуктивното (или капацитивното) и активното съпротивление:
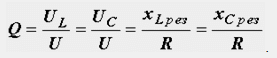
Качественият фактор показва колко пъти напрежението върху индуктивността и капацитета при резонанс надвишава напрежението, приложено към веригата. В радио вериги може да достигне няколкостотин единици.
От условието по-горе следва, че резонанс може да се постигне чрез промяна на който и да е от параметрите - честота, индуктивност, капацитет. В този случай реактивното съпротивление и импедансът на веригата се променят и в резултат на това токът, напрежението на елементите и фазовото изместване се променят. Без да анализираме формулите, ние показваме графични зависимости на някои от тези количества от капацитета (фиг. 27.2). Капацитетът C 0, при който възниква резонанс, може да се определи от формулата: C 0 =1/(ω 2 L).
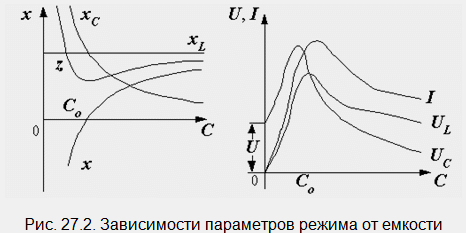
Подобно разсъждение може да се извърши за верига, състояща се от R, L и C, свързани паралелно. Векторна диаграманеговият резонансен режим е показан на фиг. 27.1, б. Нека сега разгледаме по-сложна верига с два успоредни клона, съдържащи активно и реактивно съпротивление (фиг. 27.3, а).
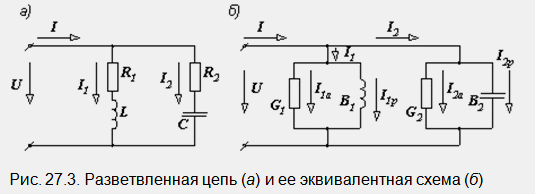
За него условието за резонанс е равенството на неговата реактивна проводимост на нула: ImY = 0. Това равенство означава, че трябва да приравним въображаемата част на комплексния израз Y на нула.
Определяме комплексната проводимост на веригата. Тя е равна на сумата от комплексните проводимости на клоните:
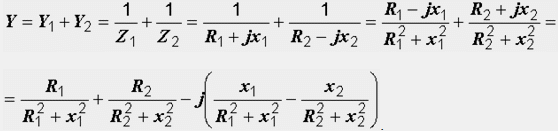
Приравнявайки израза в скоби към нула, получаваме:
Лявата и дясната част на последния израз не са нищо повече от реактивната проводимост на първия и втория клон на B1 и B2. Замяната на диаграмата на фиг. 27.3 и еквивалентен (фиг. 27.3, b), чиито параметри се изчисляват с помощта на формулите и използвайки условието за резонанс (B = B1 – B2 = 0), отново стигаме до крайния израз.
Диаграмата на фиг. 27.3, b съответства на векторната диаграма, показана на фиг. 27.4
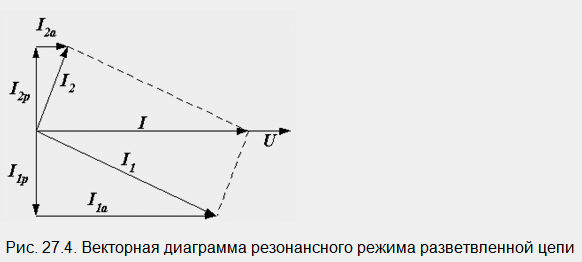
Резонансът в разклонена верига се нарича токов резонанс. Реактивните компоненти на токовете на паралелни клонове са противоположни по фаза, равни по големина и взаимно се компенсират, а сумата от активните компоненти на токовете на клона дава общия ток.
№28 Енергия и мощност във верига със синусоидален ток.
Нека на някакъв участък от веригата, чието напрежение на клемите е равно на u, токов удар азЗа времето dt се пренася електрическият заряд dq = idt. Енергията, изразходвана от източника, е равна на dw = udq = uidt, а развитата мощност p = dw/dt = ui. Тази величина се нарича моментна мощност и определя скоростта и посоката на движение на енергията в разглежданата област. Ако енергията навлиза във веригата и се натрупва в нея, функцията w(t) нараства и моментната мощност е положителна като производна на нарастващата функция. Волтаж uи ток азв тези моменти от време имат същите знаци. Процесът на натрупване на енергия във веригата се наблюдава например при зареждане на кондензатор. В онези моменти, когато uИ азимат различни знаци моментна мощносте отрицателна, функцията w(t), която определя енергията, влизаща във веригата, намалява, тъй като само намаляваща функция има отрицателна производна. Загубата на енергия в електрическа верига означава нейното връщане към източника. Тази ситуация възниква, когато кондензаторът е разреден.
Енергията, постъпваща във веригата, може да не се върне към източника, а необратимо се преобразува в топлина или механична работа. Количеството на тази енергия се определя от закона на Джаул-Ленц и за време, равно на периода на синусоидалния ток, е равно на:
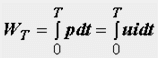
Тази стойност, свързана с времето T, определя средната стойност на моментната мощност за периода и се нарича активна мощност:
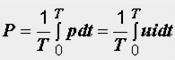
Физическа активна мощност е енергията, отделена под формата на топлина или механична работа за единица време.
Нека токът и напрежението на входа на произволна пасивна двуполюсна мрежа се описват с изразите:
Замествайки ги във формулата по-рано и интегрирайки, получаваме:
P=UIcos(φ)
Използвайки връзките между страните в триъгълниците на напрежения и токове, съпротивления и проводимости, можете да напишете верига от формули за изчисляване активна мощност:
Нека сега разгледаме енергийните процеси, протичащи в отделните елементи.
В активното съпротивление напрежението и токът са във фаза (φ = 0); във всеки момент знаците им са еднакви, моментната мощност е положителна, т.е. постоянно получава електрическа енергия, като се преобразува в топлинна или механична енергия. Активната мощност е равна на:
В реактивните елементи ъгълът на фазово изместване е 90 °. В индуктивност, при изоставащ ток, той е положителен, в капацитет, при изпреварващ ток, той е отрицателен. Като заместим φ = +- 90° в израза за напрежението на входа на веригата, получаваме u = Um sin (ωt+-90°) = +-Um cos(ωt). При това напрежение моментната мощност осцилира с двойна честота, променяйки се по синусоидален закон:
тези. променя знака два пъти за половин период. Заместването на този израз води до резултата: P = 0. Равенството на нулева активна мощност означава, че в реактивните елементи не се извършва необратимо преобразуване на електромагнитната енергия в топлинна и механична енергия.
Може да се покаже, че в индуктивността през първата четвърт от периода, когато токът нараства от нула до Im, енергията W M =(LI 2 m)/2 се натрупва в магнитното поле на индуктивността. През следващото тримесечие, когато токът намалее до нула, тази енергия от магнитно полесе връща във външната верига.
В кондензатор е подобно: през една четвърт от периода, когато напрежението върху плочите на кондензатора нараства от нула до Um, кондензаторът се зарежда, енергията се натрупва в неговото електрическо поле: W e = (CU 2 m)/2 . През следващата четвърт от периода кондензаторът се разрежда, напрежението му намалява до нула и енергията, натрупана в електрическото поле, се връща във веригата. Енергията, която електрическото поле на кондензатора и магнитното поле на намотката обменят с веригата, ще се нарича обменна енергия.
За енергията на магнитното поле W M и електрическото поле W E могат да бъдат записани следните формули:
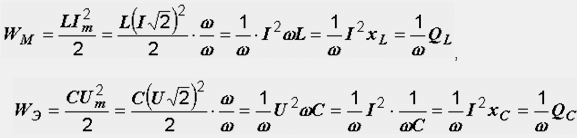
Величините Q L =I 2 X L и Q C =I 2 X C, имащи размерността на мощността, се наричат съответно реактивна мощност на индуктивност и реактивна мощност на капацитет. Те нямат нищо общо с работата, извършена от променлив ток, а са величини, пропорционални на енергията на магнитното и електрическото поле: Q L =ωW M, Q C =ωW E.
Във верига, съдържаща както индуктивност, така и капацитет, възникват енергийни флуктуации по такъв начин, че в онези моменти от време, когато магнитното поле на индуктивността натрупва енергия, електрическото поле на кондензатора освобождава енергия и обратно. Тоест, когато енергията на магнитното поле е положителна, енергията на електрическото поле е отрицателна. Общата енергия на електрическото и магнитното поле за четвърт период е равна на:
където Q е реактивната мощност на веригата, тя е пропорционална на общата енергия на електрическото и магнитното поле и може да се определи чрез реактивното съпротивление:
При резонанс, когато X L = X C , реактивните мощности Q L и Q C и енергиите W M и W E, натрупани в магнитното и електрическото поле, са равни. В този случай обменът на енергия между индуктивност и капацитет се извършва без участието на източник.
За да изчислите реактивната мощност, можете да напишете верига от формули:
При анализиране на електрически вериги често се използва триъгълник на мощността, който може да се получи чрез умножаване на страните на триъгълника на съпротивлението по квадрата на тока (фиг. 28.1). За него са валидни следните отношения:
Буквата S до хипотенузата на триъгълника показва пълна мощност. Може да се изчисли по една от следните формули:
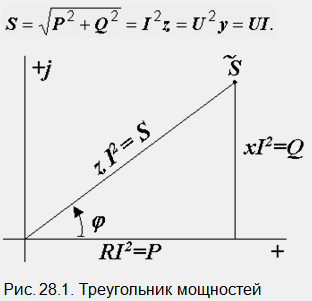
Общата мощност се определя от електрическата енергия, която се генерира от генератора и се подава към веригата. Характеризира размерите на електрическите машини и устройства. Стойността на напрежението определя нивото на изолацията - нейната дебелина и разстоянието между тоководещите честоти, а токът - напречното сечение на проводника, условията на охлаждане на машината.
Когато cosφ = 1, общата мощност е равна на най-високата стойност на активната мощност, която може да се получи при дадено напрежение и ток.
Единиците за измерване на мощността с една и съща размерност се наричат по различен начин. Единицата за активна мощност е ват (W), реактивната мощност е волт-ампер реактивен (var), привидната мощност е волт-ампер (VA).
Комплексната мощност се определя от произведението на комплекса на напрежението и комплекса на спрегнатия ток:
№29 Феноменът на взаимната индукция.
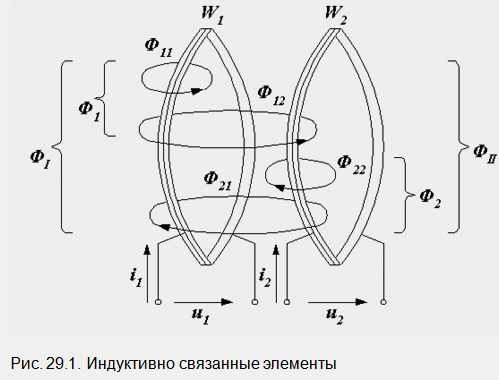
Нека има две намотки, навити под формата на тънки пръстени. Активното им съпротивление е нула, броят на навивките е W1 и W2. Намотките са разположени достатъчно близо една до друга, така че магнитното поле на всяка от тях да покрива част от съседната. Схематична картина на магнитните потоци, създадени от токове i 1 и i 2, е показана на фиг. 29.1. Всеки поток е изобразен като една силова линия, обозначена с буквата Ф с два индекса. Първият показва номера на намотката, чийто ток го създава (произхода на магнитния поток), вторият показва номера на намотката, обхваната от този поток (обекта на неговото въздействие). Нека разгледаме магнитните потоци на първата намотка. Токът създава поток Ф 1, наречен поток на самоиндукция. Неговата част F 11 покрива само първата намотка, а W E покрива и навивките на втората. Общо те са равни на F 1. Освен това завъртанията на първата намотка са обхванати от потока Ф 21, наречен взаимен индукционен поток и съставляващ част от потока Ф 2, създаден от тока на втората намотка i 2. Общият магнитен поток Ф I, преминаващ през първата намотка, се състои от потоци на самоиндукция Ф 1 и взаимна индукция Ф 21. Сумата се приема за алгебрична Ф I = Ф 1 + - Ф 21, тъй като тези потоци могат да бъдат насочени еднакво или противоположно един на друг. Изображение на фиг. 29.1 съответства на втория случай.
където ψ 1 =W 1 Ф 1 – самопоток на първата намотка (самоиндукция на потока); ψ 21 =W 1 Ф 21 – потокосцепление на взаимна индукция.
Всяка от тези връзки на потока е пропорционална на тока, който я създава: ψ 1 =L 1 i 1 и ψ 21 =Mi 2. Следователно ψ I =L 1 i 1 +-Mi 2. Когато магнитният поток се промени в бобината, се индуцира ЕДС на електромагнитна индукция и на нейните клеми се появява напрежение:
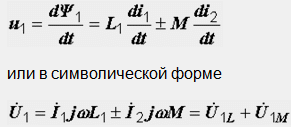
Подобно уравнение може да се напише за втората намотка.
Първият член от дясната страна на последното уравнение U 1L представлява напрежението, причинено от тока на самата намотка (напрежение на самоиндукция), а второто U 1M е напрежението, индуцирано на клемите на първата намотка от промяната магнитно поле на втората намотка (взаимно индукционно напрежение). Тези напрежения имат идентични знацикогато магнитните потоци са в една и съща посока и различни, когато са в противоположна посока.
За да се реши проблемът с естеството на връзката на намотките и посоката на техните магнитни потоци, се въвежда концепцията за едноименни скоби, маркирайки ги на диаграмата със същите икони. Маркирането се извършва въз основа на следната дефиниция.
Скоби със същото име между две намотки са тези скоби, когато при еднакви посоки на тока спрямо тези скоби магнитните потоци на самоиндукция и взаимна индукция във всяка намотка се сумират.
С други думи, ако имаме две намотки, които имат маркирани началото и края на намотката, и ако токовете в тях протичат по един и същи начин, например от началото до края и в двете намотки, тогава и двата магнитни потока във всяка от те ще бъдат съответно насочени.
Наличието на магнитна връзка между намотките се обозначава в диаграмите с двустранна дъгообразна стрелка, до която е поставена буквата i 1.
№30 Серийно свързване на индуктивно свързани елементи.
Нека две намотки със съпротивления R1 и R2, индуктивности L1 и L2 и взаимна индуктивност M са свързани последователно (фиг. 30.1).
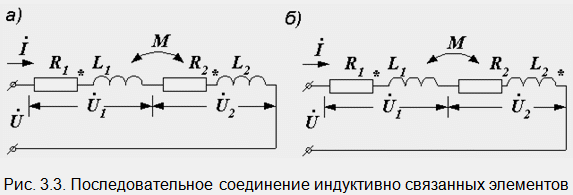
Възможни са два вида на връзката им - съгласна и контра. Ако приемем, че началото на намотките е отбелязано със звездички, тогава, когато е свързано съответно, началото на втората е свързано с края на първата (фиг. 30.1, а). Токовете в двете бобини са насочени еднакво спрямо едноименните клеми: от началото до края. Когато намотките са свързани в противоположни посоки, краят на втория е свързан с края на първия (фиг. 30.1, b).
Напрежението на всяка от намотките съдържа три компонента: спад на напрежението върху активното съпротивление, напрежение на самоиндукция и напрежение на взаимна индукция:
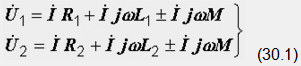
Последните имат едни и същи знаци, когато са включени съгласни и различни, когато са включени контра. Напрежението на входа на веригата е равно на сумата от тези две напрежения:
![]()
Получаваме входния комплексен импеданс на веригата от съвместно разглеждане на последните три уравнения:
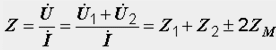
където Z1 и Z2 са комплексните съпротивления на намотките, а Z M е комплексното съпротивление на взаимната индукция:
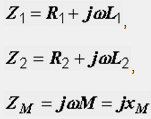
От формулата по-горе следват формули, които определят общата индуктивност на веригата и общото индуктивно съпротивление:
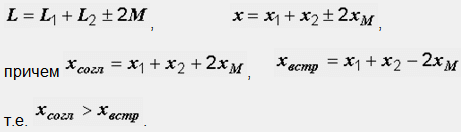
Може да се определи полученото индуктивно съпротивление на всяка бобина. За първия е равен на X 1 +-X M. И тук при включване на съгласни е по-голямо, отколкото при контра. Физически това се обяснява с факта, че в първия случай магнитният поток около всяка намотка е по-голям, отколкото във втория; например за първата намотка F Iag = F 1 + F 21 и F Iin = F 1 - F 21. В резултат на това ЕМП на електромагнитната индукция, която осигурява индуктивно съпротивление на тока, е по-голяма при превключване на съгласни, отколкото при превключване на брояч.
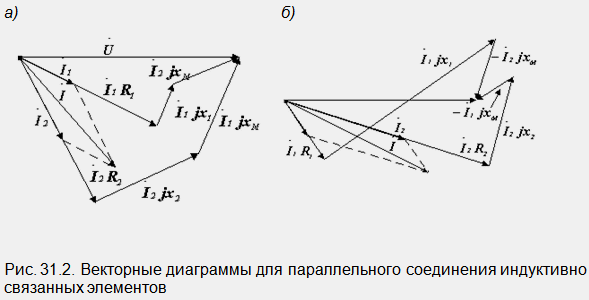
На фиг. Фигура 30.1 показва векторни диаграми, конструирани с помощта на уравнения (30.1) и (30.2).
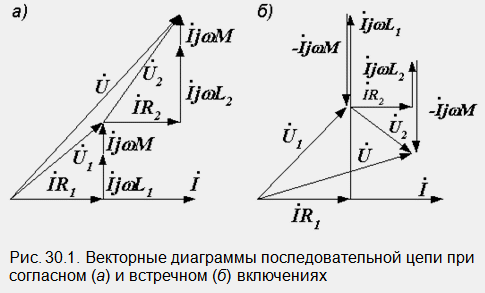
Когато са свързани в противоположни посоки, е възможен така нареченият "капацитивен" ефект, когато една от намотките има напрежение на клемите, което изостава във фаза с тока (напрежение на фиг. 30.1, b). Това се случва, когато индуктивността на бобината е по-малка от взаимната индуктивност. В този случай получената индуктивност на въпросната намотка (като се вземе предвид взаимната индукция) е отрицателна: L2-M<0. Для всей цепи такой эффект невозможен. Ее индуктивность всегда положительна, и цепь носит активно-индуктивный характер.
№31 Паралелно свързване на индуктивно свързани елементи.
противоположно. Нека две индуктивно свързани бобини с параметри R1, R2, L1, L2 и M са свързани паралелно (фиг. 3.5). Ще разгледаме и двата вида връзки едновременно. Съгласна връзка се получава чрез свързване на скоби със същото име към същия възел, брояч
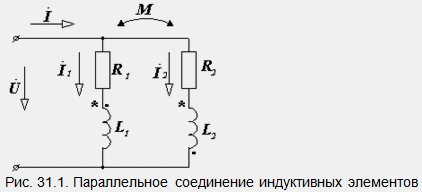
точки. Нека запишем уравненията на Кирхоф за разглежданата верига и решавайки ги, получаваме изрази, които определят токовете: Първият случай е отбелязан на диаграмата със звездички, вторият
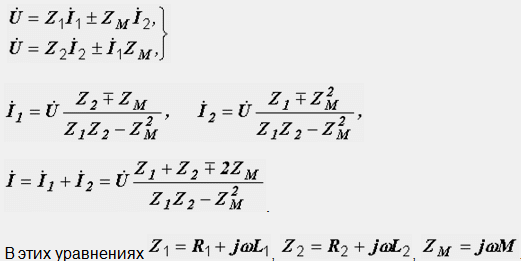
Входният комплексен импеданс на веригата е равен на съотношението на напрежението към тока на нейните клеми:
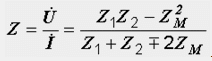
При липса на магнитно свързване между намотките, приемайки Z M = 0, получаваме добре известната формула за определяне на общото съпротивление на два паралелни клона:
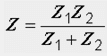
Във всички горни изрази, за термини с двоен знак, горният знак се отнася за съгласната връзка, долният знак за брояч.
На фиг. Фигура 31.2 показва векторни диаграми на разглежданата верига с връзки на съгласна (а) и контра (б) намотка. При конструирането векторите I 1 jX 1 и I 1 jX M са начертани перпендикулярно на тока I 1, а векторите I 2 jX 2 и I 2 jX M са перпендикулярни на тока I 2. При консонантна връзка взаимните индукционни напрежения водят съответните токове, а при противотокова връзка изостават от тях.
№32 Маркиране на клеми на индуктивно свързани намотки.
Ако маркировката се извършва по време на производствения процес на намотките, тогава скобите със същото име могат да бъдат обозначени чрез проследяване на посоките на навиване. За две бобини това е много лесно да се направи (фиг. 32.1, а).
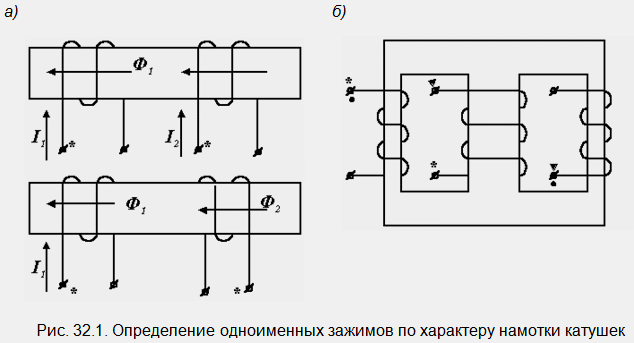
Процедираме по следния начин. Маркираме една от скобите на първата намотка с някакъв символ, например звездичка. Да приемем, че това е началото на навиването. Нека насочим тока в него от началото до края и с помощта на правилото на дясната ръка определим посоката на магнитния поток: с дясната ръка покриваме намотката така, че четири пръста да показват посоката на тока в нейните завои, след това огънатият палец ще покаже посоката на магнитния поток. Във втората намотка насочваме тока така, че неговият магнитен поток да има същата посока. Клемата, от която тече ток в бобината, също е началото. Отбелязваме го и със звездичка.
По-сложен случай е показан на фиг. 32.1, б. Оказва се, че е невъзможно да се уточнят скоби със същото име за всичките три намотки наведнъж. Трябва да ги разгледате по двойки и да действате, както току-що беше описано. В същото време, когато разглеждаме отделно двойка намотки, не обръщаме внимание на магнитната сърцевина с третата намотка.
В случай, че посоката на навиване на намотките е неизвестна и е невъзможно да се установи без разрушаване на намотката, те прибягват до помощта на електрически измервателни уреди.
Един възможен начин е следният. И двете намотки се сглобяват последователно във веригите, показани на фиг. 3.8 и свързан към източник на синусоидално напрежение със същата величина.
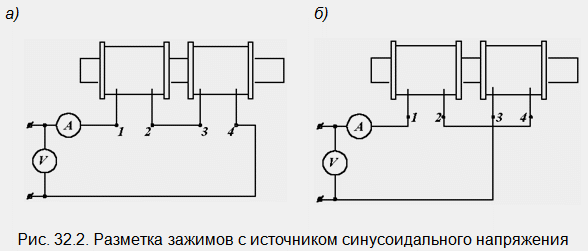
Очевидно е, че в единия случай се получава съгласна връзка, в другия - контра връзка. Видът на връзката се определя от показанията на амперметъра. Нека си припомним, че когато бобините са свързани по съгласен начин, тяхното общо съпротивление е по-голямо и следователно при една и съща стойност на входното напрежение токът е по-малък, отколкото при противоположния. И след като определихме вида на връзката, можем лесно да направим маркировките: при последователна серийна връзка намотките се свързват една с друга с противоположни скоби (началото на втората до края на първата). Ако на фиг. 33.2, при същите показания на волтметъра, амперметърът показва 1,5 A в лявата верига и 1,1 A в дясната, след това отляво имаме противоположна връзка, отдясно съгласна и следователно първата и четвъртата, както и като втората и третата са едноименните терминали.
Нека покажем друг начин за маркиране. Свързваме първата намотка чрез ключ към източник на постоянно напрежение, например към батерия; Свързваме галванометър (или волтметър) на магнитоелектрическата система към клемите на втората намотка (фиг. 32.3, а).
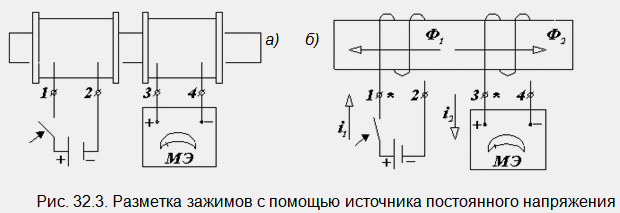
Маркираме скобата на първата намотка, свързана към положителния полюс на източника, по някакъв начин, например, като прикрепим етикет към нея. След това затваряме ключа. Ако стрелката на устройството е хвърлена върху скалата, окачваме същия етикет върху скобата на втората намотка, която е свързана към положителния извод на устройството (скоба 3). Ако стрелката се отклонява наляво, извън скалата, тогава скоба 4 е същата като скоба 1.
За да обосновем теоретично метода, ще проведем този експеримент с бобини, чиито посоки на навиване и скоби със същото име са известни (фиг. 32.3, b).
Когато ключът е затворен, в първата намотка се появява ток i 1 с нарастваща величина, който създава магнитен поток Ф 1, също нарастващ по величина. Последният индуцира електромагнитна индукция ЕДС във втората намотка. Създаденият от него ток i 2 възбужда магнитния поток Ф 2, чиято посока е противоположна на посоката на Ф 1, тъй като според принципа на Ленц той трябва да противодейства на неговото увеличаване. И магнитен поток от тази посока се създава от ток, чиято посока е показана на диаграмата. Напомняме ви, че посоките на тока в бобината и магнитния поток, който създава, са свързани с правилото на дясната ръка. Ток i 2 в разглежданата верига протича през галванометъра от положителния му извод към отрицателния. С тази посока на тока през устройството иглата му се хвърля върху скалата.
Резултатът от горните разсъждения е следното практическо правило: ако по време на експеримента, когато ключът е затворен, стрелката на устройството на магнитоелектрическата система се отклони към скалата, тогава клемите, свързани към плюса на батерията и плюса на устройствата са със същото име.
№33 Сложна схема с взаимна индуктивност.
Нека е дадена двуверижна верига, съдържаща индуктивно свързани елементи (фиг. 3.10). За да го изчислите, е необходимо да съставите три (според броя на неизвестните токове) уравнения според законите на Кирхоф. Първото уравнение, за горния възел, не създава затруднения: I1+I2-I3=0
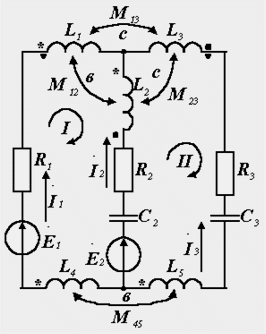
Ориз. 33.1. Сложна схема с взаимна индуктивност
Ще напишем още две уравнения съгласно втория закон на Кирхоф за контури, обозначени със заоблени стрелки I и II, показващи посоката на преминаване на контура при писане на уравненията. Но първо трябва да определите вида на връзката на намотките. За всяка двойка от тях скобите със същото име са маркирани със собствени икони. Да приемем, че това е началото на намотките. Първата и втората намотка, чиито клеми са маркирани със звездички, са свързани в противоположни посоки, тъй като в първата токът тече от началото към края, а във втората от края към началото. За памет, до стрелката M 12, нека поставим буквата b (включване на брояч). За втората и третата намотка началото на намотките е отбелязано с точки. И в двете намотки токът тече еднакво спрямо тези клеми - от началото до края, което означава, че намотките се включват съответно; Поставете буквата c до стрелката (включване на съгласни). Правим същото с останалите намотки.
Пишем уравнението за първата верига:
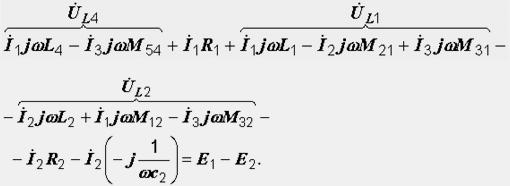
Нека дадем някои обяснения. Напрежението на клемите на намотка, индуктивно свързана с друга намотка, е сумата от напрежението на самоиндукция (IjωL) и напрежението на взаимна индукция (IjωM). Когато са включени съгласно, тези напрежения имат еднакви знаци, когато са включени противоположно, те имат различни знаци. За по-добро възприемане индексите на буквата М са поставени така, че да обозначават намотката, която създава магнитното поле (първи индекс) и намотката, в която се индуцира ЕДС (втори индекс). Например, обозначението M 32 показва, че определяме влиянието на третата намотка върху втората. Нека разгледаме компонентите на напрежението на елемента L 2. В уравнение (3.4) те са комбинирани от фигурната скоба U L2. Първият член -I2jωL е напрежението на самоиндукция. Пише се с минус, тъй като когато обикаляме веригата, вървим по този елемент срещу течението. Вторият член I1jωM 12 е напрежението, индуцирано на клемите на втората намотка от магнитния поток, създаден от тока на първата намотка. Неговият знак (плюс) поради превключването на брояча е противоположен на знака на напрежението на самоиндукция. Напрежението, което се индуцира във втората намотка от третата (I3jωM 32) има същия знак (минус) като напрежението на самоиндукция, тъй като втората и третата намотка са свързани съответно.
Ето уравнението, написано за втората верига:
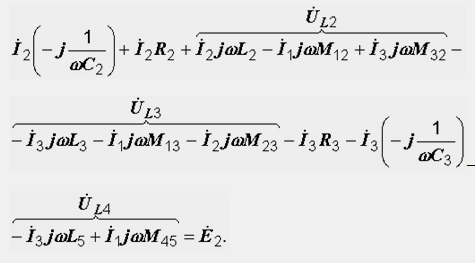
№34 Еквивалентна замяна на индуктивни съединители.
Възможно е да се избегне създаването на толкова сложни уравнения, както в предишния подраздел. За да направите това, трябва да извършите така нареченото разединяване на електрическата верига, като замените веригата с индуктивно свързани елементи с еквивалентна верига без индуктивни връзки. Това се прави съгласно следното правило: ако два елемента L 1 и L 2, имащи взаимна индуктивност, са свързани към възел на електрическа верига чрез клеми със същото име, тогава при преминаване към еквивалентната верига към тях се добавя –M елементи, а третият клон, простиращ се от възела, е включен M (фиг. 34.1, а).
Ако естеството на връзката на намотките се промени, т.е. те са свързани към възела чрез противоположни клеми, след което в еквивалентната схема знакът пред M се променя на противоположния (фиг. 34.1, b).
За да се докажат горните твърдения, е необходимо във всяка двойка вериги произволно да се посочат посоките на токовете (еднакви за същия клон) и да се запишат изразите за напреженията U ab, U bc и U ca. И за двете схеми те се оказват еднакви, което потвърждава тяхната еквивалентност.
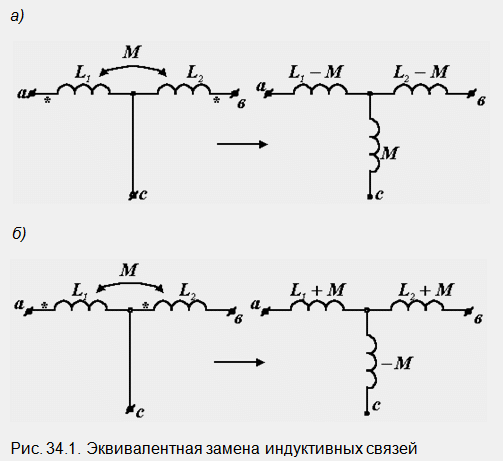
№35 Трансформатор без стоманена сърцевина.
Най-простият трансформатор е комбинация от две намотки, поставени върху обща магнитна верига (фиг. 35.1, а).
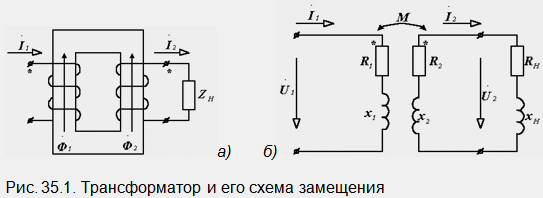
Захранващото напрежение се подава към първичната му намотка, а товарът е свързан към вторичната намотка. Изводите на едноименните намотки са техните горни изводи. Токът на първичната намотка I1 създава магнитен поток F1 в магнитната верига, което от своя страна предизвиква появата на ток I2 във вторичната намотка. Създаденият от него магнитен поток F2, в съответствие с принципа на Ленц, пречи на потока F1, т.е. насочен към него. Посоката на тока I2, съответстващ на потока F2, показан на диаграмата, се определя от правилото на дясната ръка.
Ще разгледаме трансформатор, който няма феромагнитна сърцевина. Такива трансформатори се използват при високи честоти и в специални електрически измервателни уреди. Намотките с феромагнитни сърцевини имат нелинейни характеристики и не се разглеждат тук.
Електрическата еквивалентна схема на трансформатора е показана на фиг. 35.1, б. Диаграмата показва: R1, X1, R2, X2 и - съпротивлението на първичната и вторичната намотка на трансформатора, R H и X H - съпротивлението на натоварване. Нека въведем означенията: R22=R2+R H и X22=X2+X H – общо активно и реактивно съпротивление на вторичната верига на трансформатора, Z1=R1+jX1, Z2=R2+jX2, Z H =R H +jX H, Z22 =R22+jX22 – комплексно съпротивление на съответните сечения.
Нека запишем уравненията на втория закон на Кирхоф за първичната и вторичната верига на трансформатора, като вземем предвид, че неговите намотки имат насрещна връзка:
Означавайки I1jX M =E 2M, второто уравнение на системата (35.1) може да бъде написано, както следва:
E 2M =I 2 Z 2 +I 2 Z =
Физически, E 2M е емф, която се индуцира във вторичната намотка от променливото магнитно поле на първичната намотка. Като се има предвид това, уравнението може да се прочете по следния начин: ЕМП, индуцирана във вторичната намотка на трансформатора, е равна на сумата от падовете на напрежението върху всички елементи на неговата вторична верига. Като заместим I 2 Z H =U 2, получаваме: U 2 =E 2M -I 2 Z 2. Значението на последното уравнение е следното: напрежението на вторичните изводи на трансформатора е по-малко от ЕДС, индуцирана във вторичната намотка с количеството на спада на напрежението върху нейното съпротивление.
На фиг. Фигура 35.2 показва векторна диаграма на трансформатор. Започваме изграждането му с вторичния ток I2. Фокусирайки се върху неговата посока, рисуваме вектори на напрежението върху всички елементи на вторичната верига. Тяхната сума е равна на ЕДС E 2M. Тъй като формулата, която определя неговата стойност, съдържа коефициент j, който завърта вектора с една четвърт оборот, ние провеждаме тока под ъгъл от 90° към E 2M в посоката на изоставането. След като определихме посоката на I1, конструираме векторите I1R1 и I1jX1, които в сумата с I2jX M дават U1.
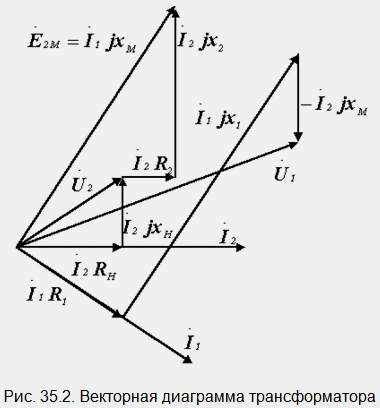
За анализ на работата на трансформатор се използват различни еквивалентни схеми. Нека разгледаме някои от тях.
Чрез свързване на двата долни извода на трансформатора (режимът му на работа няма да се промени) и разединяване на индуктивните връзки стигаме до Т-образна еквивалентна схема (фиг. 35.3).
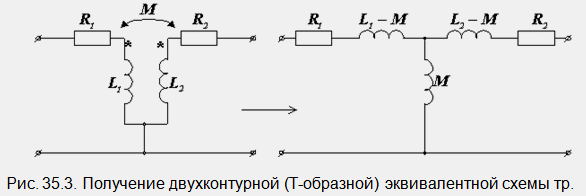
От второто уравнение на системата изразяваме тока I2 и го заместваме в първото уравнение на същата система:
Последният израз съответства на диаграмата, показана на фиг. 35.3. Съпротивлението Z BH, свързано последователно с Z1, се нарича вложено (от вторичната верига на трансформатора към първичната).
Както следва от формулата, тя е равна на:
Неговите активни и реактивни компоненти са съответно равни:

Появата на активно съпротивление в първи контур, въведено от първи контур, физически означава следното. Енергията, подадена към трансформатора, се консумира не само от съпротивлението R1, но и от съпротивленията на вторичната верига R2 и RH, където се предава чрез променливо магнитно поле между намотките.
Поради минуса във въведената формула за съпротивление, общото съпротивление на цялата верига, равно на сумата от X1 и X BH, се оказва по-малко от индуктивното съпротивление на първичната намотка.
Това съвпада добре с казаното по-рано. Когато намотките на трансформатора са свързани в противоположни посоки, потокът F2, насочен срещу потока F1, намалява последния, което води до намаляване на общото индуктивно съпротивление.
№36 Трифазна система.
Многофазна система е набор, състоящ се от “n” отделни еднакви електрически вериги или електрически вериги, работните параметри в които (e, u, i) са изместени във времето с равни сегменти Δt=T/n или във фаза Δωt=2π/ n=360°/n.
Отделните части на системата се наричат фази. Терминът "фаза" в електротехниката има две значения: първото - като момент във времето за синусоидална функция на тока или напрежението, второто - като част от многофазна система. В технологията са използвани 2, 3, 6 и повече фазови системи. В електроенергетиката най-разпространената трифазна система има редица предимства пред системите с различен брой фази.
Трифазна система се състои от три електрически вериги или електрически вериги (фази), параметрите на режима (u,i) в които са изместени във времето с Δωt=2π/3=360°/3=120°. Отделните фази на трифазна система съгласно GOST са обозначени (наименувани) с главни латински букви A, B, C (основно обозначение) или цифри 1, 2, 3 (допустимо обозначение) или главни латински букви R, S , T (международно обозначение).
Няма значение коя от трите фази с коя буква A, B или C се нарича, важен е редът, в който те следват една след друга във времето. Директният ред на фазите се нарича A→B→C→A, при който параметрите на режима (u, i) във фаза B изостават от подобни параметри във фаза A със 120°, а във фаза C те изпреварват със 120°. °. При обратен ред на фазите A→C→B→A, параметрите на режима във фаза C изостават от подобни параметри във фаза A с 120°, а във фаза B те изпреварват със 120°.
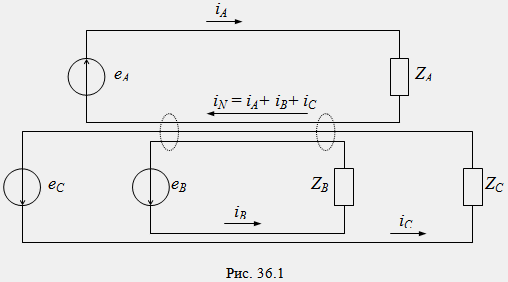
Ако отделните фази на една система работят изолирано и независимо една от друга, тогава системата се нарича несвързана. Нека разгледаме работата на най-простата несвързана трифазна система (фиг. 36.1). Моментните стойности на фазовата ЕМП на генератора се изместват във времето с 120 ° в реда на фази A→B→C→A:
e A =E m sinωt ↔ E A =Ee j0°
e B =E m sin(ωt-120°) ↔ E B =Ee -j120°
e C =E m sin(ωt-240°)=E m sin(ωt+120°) ↔ E C =Ee j120°
Графичните диаграми на тези функции са показани на фиг. 36.2, а векторните - на фиг. 36.3.
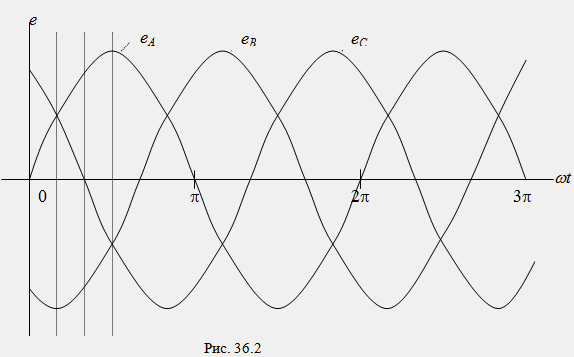
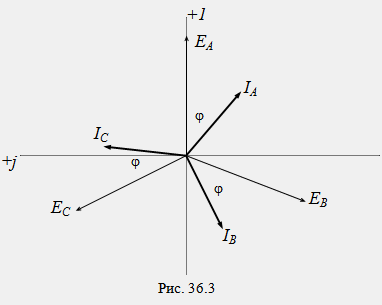
Основното свойство на всяка променлива функция (e, u, i) в симетрична трифазна система е, че сумата от техните моментни стойности по всяко време е нула, например e A + e B + e C = 0 Нека намерим тази сума за различни моменти от време:
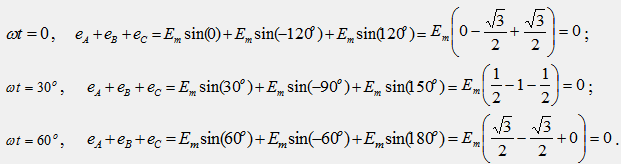
Ако натоварването на отделните фази е равно помежду си, т.е. Z A =Z B =Z C =Ze jφ , тогава фазови токовеще бъдат еднакви по големина и изместени във фаза спрямо тяхната ЕМП (напрежение) със същия ъгъл φ, а помежду си, подобно на ЕМП, ще бъдат изместени във фаза със 120°. Следователно фазовите токове i A, i B, i C образуват симетрична трифазна система и за тях ще бъдат валидни предварително получените заключения: i A + i B + i C = 0; I A + I B + I C = 0.
Преобразуваме несвързана трифазна система в свързана, като комбинираме три връщащи задвижвания в едно общо задвижване. Съгласно първия закон на Кирхоф общият ток i N = i A + i B + i C = 0 трябва да протича в общия проводник. Това означава, че изобщо няма нужда от обратен проводник, което води до значителни икономии на проводници при предаване на енергия от трифазен генератор към приемника.
Предимства (предимства) на трифазна система:
1) Прехвърлянето на енергия от генератора към потребителите с помощта на трифазен ток е икономически по-изгодно, отколкото с всеки друг брой фази. Например, в сравнение с двупроводна система, икономията на проводници се постига наполовина (3 проводника вместо 6), а загубите на енергия в линейните проводници съответно намаляват.
2) Трифазната система прави технически лесно получаването на кръгово въртящо се поле, което е в основата на работата на всички трифазни машини (генератори и двигатели).
3) Елементите на трифазна система (генератори, трансформатори, двигатели) са прости по дизайн, надеждни при работа, имат добри характеристики на тегло и размери, сравнително евтини и издръжливи.
4) На изхода трифазни генераториИма две нива на изходно напрежение - линейно и фазово, различаващи се с √3 пъти (Ul / Uph = √3), което ви позволява да свържете приемници с различни номинални напрежения към такъв генератор.
Поради своите предимства трифазната система се използва в електроенергетиката за производство, пренос, разпределение и потребление на електрическа енергия.
Трифазната система и нейните основни компоненти - генератор, трансформатор, електропреносна линия, двигател - са разработени през 1889 г. от инженер Доливо-Доброволски (Siemens и Schuckert). Създаването на тази система беше важно събитие в историята на развитието на теоретичната и приложна електротехника.
№37 Методи за свързване на намотки на трифазни генератори.
В намотките на трифазен генератор се индуцират синусоидални ЕМП, изместени във фаза с 120 °:
e A =E m sinωt ↔ E A =E f e j0°
e B =E m sin(ωt-120°) ↔ E B =E f e -j120°
e C =E m sin(ωt-240°)=E m sin(ωt+120°) ↔ E C =E f e j120°
Фазовите намотки на генератора могат да бъдат свързани една към друга според две различни вериги: звезда (y) и триъгълник (Δ).
Когато са свързани в звезда, краищата на фазовите намотки (фази) на генератора са свързани към обща точка N, която се нарича нула или неутрална, а началото на намотките служат като линейни клеми на генератора A, B , C (фиг. 37.1).
Векторната диаграма на напрежението на трифазен генератор, когато неговите фазови намотки са свързани в звезда, е показана на фиг. 37.2 а, б.
В трифазен генератор се разграничават фазови и линейни напрежения. Фазовите напрежения се наричат напрежения между началото и края на фазовите намотки или между един от линейните клеми A, B, C и нулевия извод N. Фазовите напрежения са равни на фазовата EMF: U A = E A, U B = E B, U C = E C (индексът N се понижава при фазови напрежения, тъй като φ N = 0). Линейни напрежения се наричат напрежения между две линейни клеми A, B, C. Линейните напрежения са равни на векторната разлика на две фазови напрежения: U AB =U A - U B; U BC = U B - U C; U CA = U C - U A.
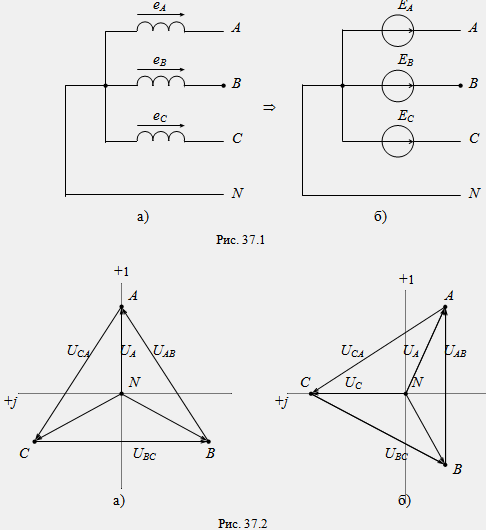
При изчисляване на трифазни вериги по комплексния метод фазовите и линейните напрежения на генератора се представят в сложна форма, докато един от системните вектори се приема като начален и се комбинира с реалната ос, а останалите вектори получават начални фази според техните ъгли на изместване спрямо началния вектор. На фиг. 37.2а показва вариант за представяне на напреженията на трифазен генератор в сложна форма, когато фазовото напрежение на фаза А се приема като начален вектор.В този случай фазовите напрежения на генератора в сложна форма ще приемат формата : U A =U f e j0°, U B =U f e -j120°, U C =U f e j120°, линейни напрежения: U AB =U l e j30°, U BC =U l e -j90°, U CA =U l e j150° .
На фиг. Фигура 37.2 b показва друга опция за представяне на напреженията на трифазен генератор в сложна форма, когато линейното напрежение U AB се приема като начален вектор. В този случай фазовите напрежения на генератора в сложна форма ще бъдат под формата: U A =U f e -j30°, U B =U f e -j150°, U C =U f e j90°, линейни напрежения: U AB =U l e j0 °, U BC =U l e -j120° , U CA =U l e j120° .
От геометрията получаваме връзката между модулите на линейните и фазовите напрежения: U L = 2U Ф cos 30° =2UФ √(3)/2 =√(3) UФ.
Намотките на трифазен генератор теоретично могат да бъдат свързани според триъгълна верига. В такава схема краят на всяка предишна фаза е свързан с началото на следващата, а точките на свързване служат като линейни клеми на генератора (фиг. 37.3).
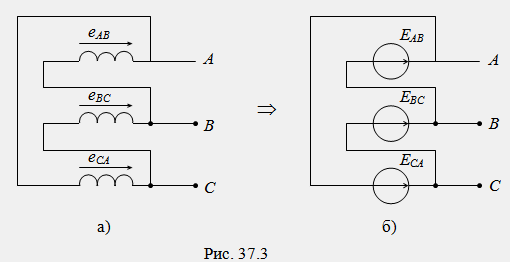
Когато фазите са свързани в триъгълник, в неговата верига действа сумата от фазовия ЕМП: ∑e = e AB + e BC + e CA. В реалните трифазни генератори е технически невъзможно да се гарантира, че общата EMF е равна на нула. Тъй като собственото съпротивление на намотките на генератора е малко, дори незначителен общ ЕМП ∑e > 0 може да предизвика изравнителен ток в триъгълната верига, съизмерим с номиналния ток на генератора, което би довело до допълнителни загуби на енергия и намаляване на ефективността на генератора. Поради тази причина намотките на трифазните генератори не трябва да се свързват в триъгълник.
Номиналното напрежение в трифазна система се нарича мрежово напрежение. Номиналното напрежение обикновено се изразява в киловолти (kV). Използваната в практиката скала на номиналните трифазни напрежения е: 0,4; 1.1; 3,5; 6.3; 10,5; 22; 35; 63; 110; 220; 330; 500; 750. На потребителско ниво номиналното трифазно напрежение може да се посочи като съотношението U L ⁄U F, например: U L /U F = 380 ⁄ 220 V.
№
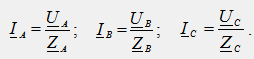
I N =I A +I B +I C
I A +I B +I C =0
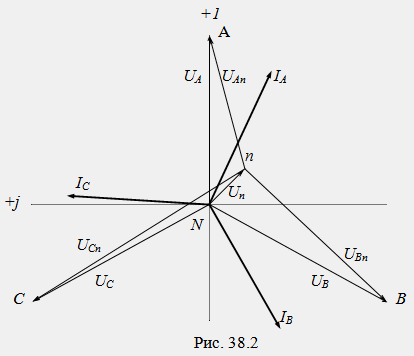
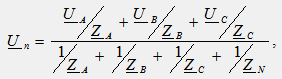
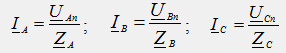
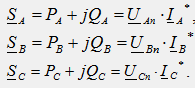
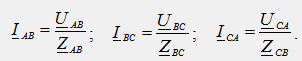
№38 Методи за свързване на фазите на трифазни приемници.
Трифазните приемници на ток могат да бъдат свързани към генератора с помощта на две вериги - звезда (y) и триъгълник (Δ). Както е известно, на изхода на трифазен генератор се получават две напрежения (линейно и фазово), различаващи се с фактор Ul/Uph = √3 пъти. От друга страна, всеки енергиен приемник е проектиран да работи при определено напрежение, което се нарича номинално напрежение. Диаграмата на фазово свързване на приемника трябва да гарантира, че неговите фази са свързани към номиналното фазово напрежение. По този начин изборът на диаграма на фазово свързване за трифазен приемник зависи от съотношението на номиналните напрежения на приемника и генератора (мрежата).
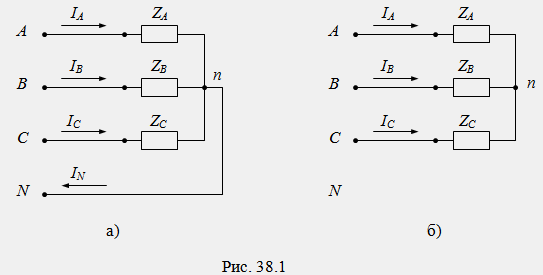
Звездата се използва, ако номиналното напрежение на приемника съответства (равно на) фазовото напрежение на генератора. Когато са свързани в звезда, краищата на фазите на приемника се комбинират в една точка "n", наречена нула или неутрална, а началото на фазите е свързано към линейните клеми на трифазния генератор A, B, C с линейни проводници. Ако нулевата точка на приемника "n" е свързана с нулевата точка на генератора "N" чрез неутрален проводник, тогава веригата се нарича звезда с неутрален проводник (фиг. 38.1а). С отсъствие неутрален проводникверигата се нарича звезда без неутрален проводник (фиг. 38.1b).
Токове, протичащи в линейни проводници в посока от генератора към приемника, се наричат линейни.
Токове, протичащи във фазите на приемника в посока от началото до края, се наричат фазови токове. Във веригата звезда фазите на приемника са свързани последователно с линейните проводници и през тях протичат еднакви токове (I A, I B, IC). Следователно за звездна верига понятията за линейни и фазови токове са идентични: I L = I F.
Токът, протичащ в неутралния проводник от приемника към генератора, се нарича нулев или неутрален (I N).

Напреженията между началото и края на фазите на приемника се наричат фазови (U An, U Bn, U Cn), а напреженията между началото на фазите се наричат линейни (U AB, U BC, U CA). Линейните напрежения на приемника и генератора са идентично равни.
В звездна верига с неутрален проводник (фиг. 38.1a) фазовото напрежение на генератора се подава директно към всяка фаза на приемника (U AN = U An = U A, U BN = U Bn = U B, U CN = U Cn = U C), всяка от фазите в този случай работи независимо една от друга, а линейните (фазови) токове се определят съгласно закона на Ом:
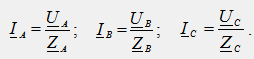
Токът в нулевия проводник, в съответствие с първия закон на Кирхоф, е равен на геометричната сума на линейните (фазови) токове:
I N =I A +I B +I C
При симетричен товар Z A =Z B =Z C токът в неутралния проводник е I N =0 и следователно няма нужда от него. Симетричните трифазни приемници (например трифазни електродвигатели) са свързани по звездна верига без неутрален проводник.
При асиметрично натоварване относителната величина на тока в нулевия проводник зависи от естеството и степента на асиметрия на фазовите токове. По правило трифазните приемници са проектирани възможно най-близо до симетрични, така че токът в нулевия проводник в реални условия е значително по-малък от линейните (фазови) токове.
в звездна верига без неутрален проводник (фиг. 38.1b), за всяко фазово натоварване трябва да бъде изпълнено условието на първия закон на Кирхоф:
I A +I B +I C =0
От уравнението следва, че промяната в един от токовете води до промяна в другите два тока, т.е. отделните фази работят в режим, зависим един от друг. При асиметрично натоварване потенциалът на нулевата точка на приемника Un става не равен на нула, той се „измества“ в комплексната равнина от нулева позиция, докато фазовите напрежения на приемника (U An, U Bn, U Cn ) не са равни на съответните фазови напрежения на генератора (U A, U B, U C), възниква така нареченото несъответствие на фазовите напрежения на приемника (фиг. 38.2).

Изчисляването на токове и напрежения в звездна верига без неутрален проводник се извършва в следната последователност.
Напрежението (потенциал) на неутралната точка на приемника се определя по метода на два възела:
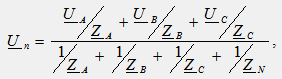
където Z N е комплексното съпротивление на нулевия проводник, при липса на Z N =∞.
Фазовите напрежения на приемника се определят като потенциални разлики на съответните точки:
U An =U A -U n, U Bn =U B -U n, U Cn =U C -U n.
Фазовите токове на приемника се определят от закона на Ом:
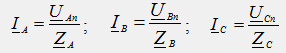
Комплексни фазови мощности на приемника:
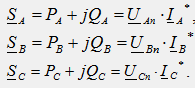
Режимът на работа на приемника с дисбаланс на фазовото напрежение е ненормален и може да доведе до неговата повреда. Поради тази причина асиметричен трифазен товар не трябва да се свързва в звездна верига без неутрален проводник (например товар за осветление).
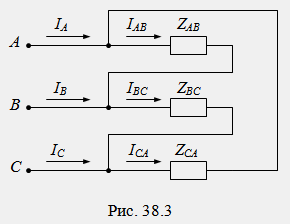
Веригата триъгълник се използва, ако номиналното фазово напрежение на приемника съвпада (равно е) с мрежовото напрежение на генератора. При свързване в триъгълник краят на всяка фаза се свързва с началото на следващата, а точките на свързване (върховете на триъгълника) се свързват към линейните клеми на трифазния генератор A, B, C с линейни проводници (фиг. 38.3).
Токове, протичащи във фазите на приемника в посока от началото към края им, се наричат фаза (I AB, I BC, I CA). Токове, протичащи в линейни проводници в посока от генератора към приемника, се наричат линейни (I A, I B, IC).

В триъгълна верига фазовото и линейното напрежение на приемника са еднакви (U AB, U BC, U CA). При тази схема линейното напрежение на генератора се подава директно към всяка фаза на приемника, докато отделните фази работят независимо една от друга. Фазовите токове се определят от закона на Ом:
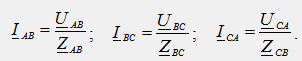
Линейните токове се определят от уравненията на първия закон на Кирхоф за върховете на триъгълника; те са равни на геометричната разлика на фазовите токове:
I A =I AB -I CA ; I B =I BC -I AB ; I C =I CA -I BC.
При симетричен режим фазовият и линейният ток са симетрични, а отношението на техните модули е IЛ/IF = √3.
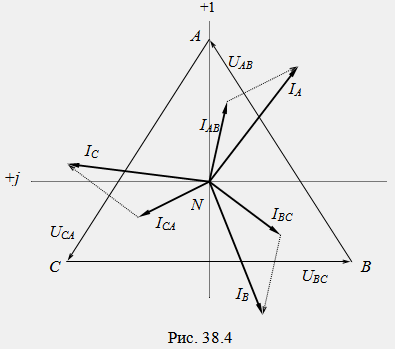
При асиметрично натоварване връзката между линейните и фазовите токове се определя от уравненията на първия закон на Кирхоф. На фиг. Фигура 38.4 показва векторна диаграма на токове и напрежения за произволна трифазна верига, когато фазите са свързани в триъгълник.

№39 Изчисляване на сложни трифазни вериги.
Сложна трифазна верига, като например взаимосвързана енергийна система, може да съдържа голям брой трифазни генератори, електропроводи и трифазни енергийни приемници. Схемата на такава верига е типичен пример сложна веригапроменлив ток. Стационарното състояние в такава верига може да се опише чрез система от алгебрични уравнения със сложни коефициенти, съставени с помощта на един от методите за изчисляване на сложни вериги (метод на законите на Кирхоф, метод на токове на веригата, метод на възлови потенциали). Най-рационалният метод за изчисляване на такива трифазни вериги е методът на възловите потенциали, при който уравненията се изготвят и решават в матрична форма.
В по-прости случаи е възможно да се използват всякакви методи за изчисление, които позволяват получаване на икономично решение на проблема. На фиг. Фигура 39.1 показва диаграма на паралелно свързване на няколко трифазни приемника с различни схеми на фазово свързване към един генератор. В представената диаграма изчисляването на фазовите и линейните токове на всеки от приемниците може да се извърши поотделно и независимо един от друг, а линейните токове на източника се определят като геометрични суми от токовете на всички приемници, например IA = I A1 + I A2 + I A3.
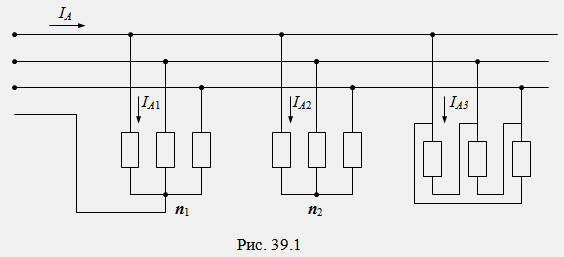
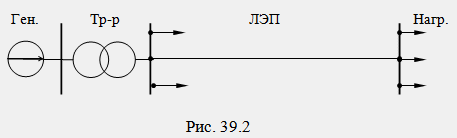
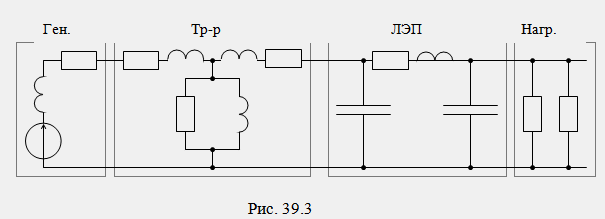
Както е известно, интегрираната трифазна система за захранване работи в режим, близък до симетричния. В симетричен режим токовете и напреженията на съседните фази се различават само в ъгъла на изместване с ±120º. Изчисляването на токове и напрежения в стационарен симетричен режим се извършва само за една от фазите, например за фаза А, докато трифазните вериги са представени от еднофазни еквивалентни вериги. На фиг. Фигура 39.2 показва символична диаграма на пренос на енергия от трифазен генератор към отдалечени приемници, а на фиг. 39.3 – изчислена монофазна схема за същата верига. В изчислителната диаграма Фиг. 39.3 всяка връзка за предаване на енергия съответства на своята стандартна еквивалентна схема.
В резултат на изчисленията се определят токове и напрежения във всички елементи на веригата за фаза A, например I A =Ie jα. Подобни токове и напрежения във фаза B се определят чрез умножаване на съответните стойности на фаза A с фактора на въртене e -j120°, а за фаза C с фактора e j120°.
№40 Мощност на трифазна верига и методи за нейното измерване.
Активната и реактивната мощност на трифазна верига, както за всяка сложна верига, са равни на сумите от съответните мощности на отделните фази:
където I A, U A, I B, U B, I C, U C са фазовите стойности на токовете и напреженията.
В симетричен режим мощностите на отделните фази са равни и мощността на цялата верига може да се получи чрез умножаване на фазовите мощности по броя на фазите:
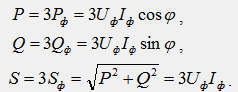
В получените изрази заменяме фазовите величини с линейни. За звездната диаграма следните съотношения са правилни: Uph/Ul/√3, I f =I l, тогава получаваме:
За триъгълната диаграма са правилни съотношенията: Uф=Uл; Ако = Iл / √3, тогава получаваме:
Следователно, независимо от схемата на свързване (звезда или триъгълник) за симетрична трифазна верига, формулите за мощност имат същата форма:
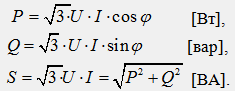
В дадените формули за мощностите на трифазна верига се подразбират линейни стойности на величините U и I, но индексите не се използват в техните обозначения.
Активната мощност в електрическа верига се измерва с устройство, наречено ватметър, чиито показания се определят по формулата:
където U w, I w са векторите на напрежението и тока, подавани към намотките на устройството.
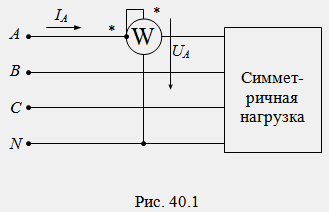
За измерване на активната мощност на цялата трифазна верига, в зависимост от схемата на свързване на фазите на натоварване и нейния характер, различни схемивключване на измервателни уреди.
За измерване на активната мощност на симетрична трифазна верига се използва схема с един ватметър, който е свързан към една от фазите и измерва активната мощност само на тази фаза (фиг. 40.1). Активната мощност на цялата верига се получава чрез умножаване на показанията на ватметъра по броя на фазите: P=3W=3U f I f cos(φ). Единичната верига на ватметър може да се използва само за ориентирана оценка на мощността и не е приложима за прецизни и търговски измервания.
За измерване на активна мощност в четирипроводник трифазни вериги(при наличие на неутрален проводник) се използва верига с три устройства (фиг. 40.2), в която активната мощност на всяка фаза се измерва отделно и мощността на цялата верига се определя като сума от показанията от три ватметра:
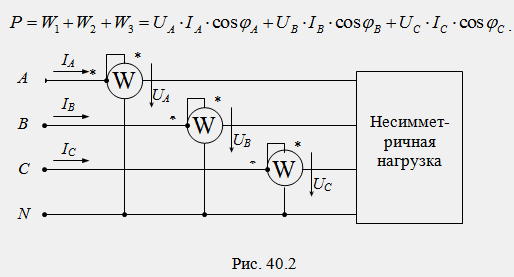
За измерване на активната мощност в трипроводни трифазни вериги (при липса на неутрален проводник) се използва верига с две устройства (фиг. 40.3).
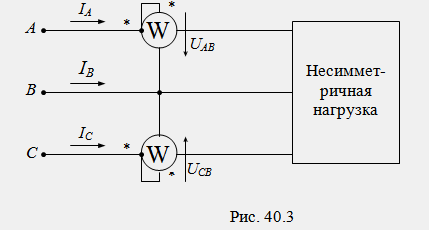
При липса на неутрален проводник линейните (фазови) токове са свързани помежду си чрез уравнението на първия закон на Кирхоф: I A + I B + I C = 0. Сумата от показанията на два ватметъра е равна на:
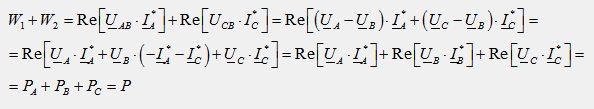
По този начин сумата от показанията на два ватметъра е равна на активната трифазна мощност, докато показанието на всяко устройство поотделно зависи не само от размера на товара, но и от неговия характер.
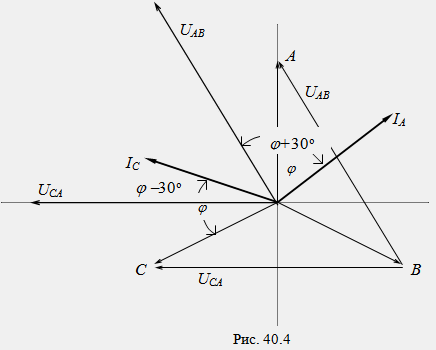
На фиг. Фигура 40.4 показва векторна диаграма на токове и напрежения за симетричен товар. От диаграмата следва, че показанията на отделните ватметри могат да бъдат определени по формулите:
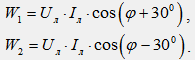
Анализът на получените изрази ни позволява да направим следните изводи. При активно натоварване (φ = 0) показанията на ватметъра са равни (W1 = W2).
При активно-индуктивен товар (0 ≤ φ ≤ 90°), отчитането на първия ватметър е по-малко от втория (W1< W2), а при φ>60° показанието на първия ватметър става отрицателно (W1<0).
При активно-капацитивен товар (0 ≥ φ≥ -90°), показанието на втория ватметър е по-малко от първия (W1 е по-голямо от W2), а при φ (по-малко от) -60°, показанието на вторият ватметър става отрицателен.
№41 Въртящо се магнитно поле.
Едно от най-важните предимства на трифазната система е възможността с нейна помощ да се получи кръгово въртящо се магнитно поле, което е в основата на работата на трифазни машини (генератори и двигатели).
За да се получи кръгово въртящо се магнитно поле, е необходимо и достатъчно да бъдат изпълнени две условия. Условие едно: необходимо е да се разположат 3p еднакви намотки (p = 1, 2, 3,….) в пространството, така че осите им да са разположени в една равнина и взаимно изместени под равни ъгли ∆α = 360°/3p. Условие второ: през бобините е необходимо да преминават променливи токове, еднакви по амплитуда и изместени във времето с ∆t=T/3 или ∆ωt = 360°/3=120° (симетричен трифазен ток). При спазване на посочените условия в пространството около намотките ще се създаде кръгово въртящо се магнитно поле с постоянна амплитуда на индукция B max по оста й и с постоянна ъглова скорост на въртене ωп.
На фиг. Фигура 41.1 показва пространственото разположение на три (p = 1) еднакви намотки под равни ъгли от 120° според първото условие.
През бобините протича симетричен трифазен ток в посока от началото им (A, B, C) към краищата им (X, Y, Z):
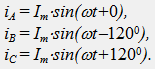
Магнитното поле, създадено от всяка отделна намотка, е пропорционално на тока на намотката (B = k*i), следователно магнитните полета на отделните намотки в координатния център образуват симетрична трифазна система B(t):
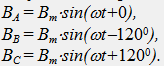
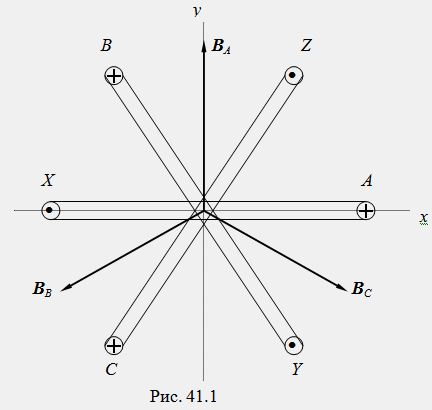
Положителните посоки на магнитните полета на всяка бобина (вектори B A, B B, B C) в пространството се определят от правилото на десния винт според приетите положителни посоки на токовете на бобината (фиг. 41.1).
Полученият вектор B на индукция на магнитно поле за всеки момент от времето може да бъде намерен чрез пространствено събиране на векторите B A, B B, B C на отделните намотки. Нека определим стойността на резултантния вектор на индукция на магнитното поле B за няколко момента от време ωt = 0°; 30°; 60°. Пространственото добавяне на вектори ще извършим графично (фиг. 41.2a, b, c). Резултатите от изчислението са обобщени в отделна таблица:
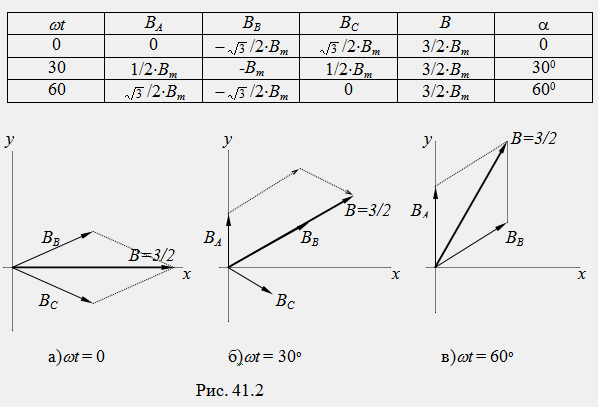
Анализът на таблицата показва, че резултантният вектор на индукция на магнитно поле B(t,x,y) има постоянна амплитуда (B max =3/2B m) и се върти равномерно в пространството в положителна посока в посоката от намотка A към намотка B с ъглова скорост ωп, равна на ъгловата честота на тока ω. В общия случай ъгловата скорост на въртене на магнитното поле също зависи от броя на намотките:
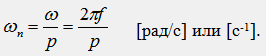
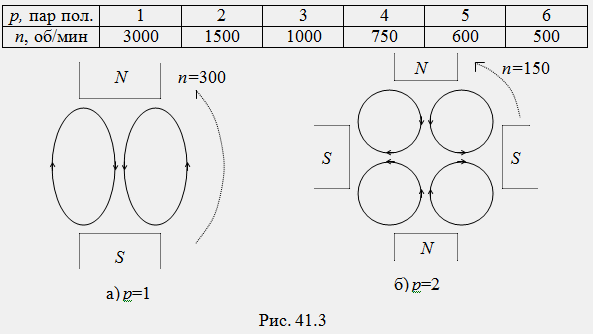
В технологията, за да се характеризира въртенето на магнитно поле, се използва понятието честота на въртене: n=60f/p [rpm]
Тъй като числото p се променя, пространственият модел на магнитното поле се променя: когато p=1, магнитното поле има два полюса (или една двойка полюси), когато p=2 има четири полюса (или 2 двойки полюси) и т.н. . (фиг. 41.3). По тази причина числото p = 1, 2, 3,... се нарича брой двойки полюси на магнитното поле.
Честотата на въртене на магнитното поле може да се променя плавно чрез промяна на честотата на захранващия ток f и стъпаловидно чрез промяна на броя на двойките полюси p. В индустриални условия и двата метода за регулиране на честотата на въртене на полето са технически и икономически неефективни. При постоянна честота на промишления ток f=50 Hz, скалата на синхронните честоти на въртене на магнитното поле като функция от броя на двойките полюси е както следва:
За да промените посоката на въртене на магнитното поле, достатъчно е да промените реда на фазите на захранващия ток или просто да размените всеки две фази на източника една с друга.
№42 Теоретични основи на метода на симетричните компоненти.
Методът на симетричните компоненти се използва за изчисляване на трифазни вериги в асиметрични режими. Асиметричните режими в електроенергийната система възникват от различни видове къси съединения. Изчисляването на токовете на късо съединение е важен инженерен проблем в електроенергетиката, който се решава по метода на симетричните компоненти.
Математически всяка асиметрична трифазна система от векторни величини (напрежения, токове и т.н.) може да бъде представена като сума (заместена със сума) от три симетрични трифазни системи, а именно: а) системи с директна последователност с директен ред на фазите A→B→C→ A; б) системи с обратна последователност с обратен фазов ред A→C→B→A; в) системи с нулева последователност, които се състоят от три еднакви вектора, които са във фаза. Индивидуалните симетрични системи от вектори, на които се разлага една асиметрична система, се наричат симетрични компоненти. Векторите на симетричните компоненти са индексирани с числа: 1 - за положителната редица, 2 - за отрицателната редица и 0 - за нулевата редица.
На фиг. 42.1 показва симетричните компоненти на някои асиметрични трифазни напрежения U A, U B, U C.
В метода на симетричните компоненти за опростяване на формата на записване на уравненията се използва коефициентът a=e j120° (коефициент на въртене), умножен по който векторът се завърта на ъгъл 120°, без да се променя модулът му. Свойства на фактора на ротация: a 2 =e j240° =e -j120°, a 3 =1, a 4 =a, 1+a+a 2 =0.
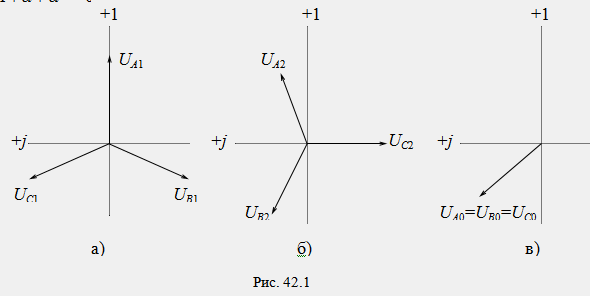
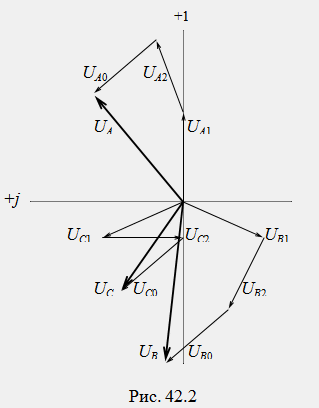
Векторите на оригиналната асиметрична система се определят от принципа на суперпозицията като геометрични суми на съответните вектори на симетрични компоненти:
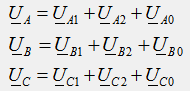
Геометричното добавяне на вектори на симетрични компоненти съгласно тези уравнения е показано на фиг. 42.2.
Използвайки фактора на ротация „a“ и „a 2“, ние изразяваме всички членове от дясната страна на уравненията чрез симетричните компоненти на фаза A:
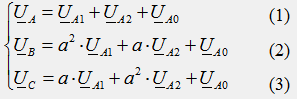
Нека умножим всички членове на уравнение (2) по “a” и всички членове на уравнение (3) по “a 2”, съберем и трите уравнения член по член и получим:
От полученото уравнение следва формула за изолиране на симетричния компонент на директната последователност от асиметрична система от вектори:
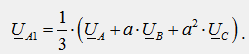
Нека умножим всички членове на уравнение (2) по “a 2” и всички членове на уравнение (3) по “a”, съберем и трите уравнения член по член и получим:
От полученото уравнение следва формула за изолиране на симетричния компонент на обратната последователност от асиметрична система от вектори:
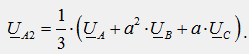
Нека съберем и трите уравнения (1), (2) и (3) член по член и ще получим:
От полученото уравнение следва формула за изолиране на симетричния компонент на нулевата последователност от асиметрична векторна система:
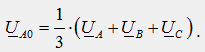
Получените формули се използват на практика за разлагане на асиметрични трифазни векторни системи на симетрични компоненти.
№43 Изчисляване на симетричен трифазен режим на натоварване при несиметрично напрежение.
Нека към симетричен трифазен приемник, например електродвигател, се приложи система с асиметрично напрежение U A, U B, U C. За да получим общи принципи, въвеждаме неутрален проводник със съпротивление Z N във веригата. Схемата на веригата ще приеме формата (фиг. 43.1):
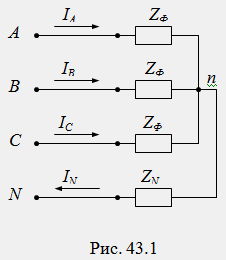
Нека разложим асиметричната система от напрежения U A, U B, U C на симетрични компоненти на директните, отрицателните и нулевите последователности:
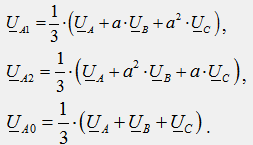
Нека приложим метода на суперпозиция към изчисляването на веригата и да изчислим токовете отделно за всеки симетричен компонент на напрежението. Тъй като за всеки от симетричните компоненти трифазната верига генератор-приемник е напълно симетрична, изчислението на режима може да се извърши само за една фаза А; съответно трифазната верига трябва да бъде заменена с три еднофазни вериги отделно за всяка компонент (фиг. 43.2a, b, c). В симетричен режим за положителни и отрицателни последователности токът в неутралния проводник е нула и следователно напрежението U nN = 0. Това означава, че съпротивлението в нулевия проводник Z N не влияе на фазовите токове и не трябва да се включва във вериги за тези последователности (фиг. 43.2 a, b). Токовете на нулева последователност във всички фази са еднакви и могат да бъдат затворени само през неутралния проводник: I N = I A0 + I B0 + I C0 = 3I A0. Съгласно втория закон на Кирхоф за нулевата последователност (фиг. 43.1), получаваме:
U A0 = I A0 Z 0 + I N Z N = I A0 (Z 0 + 3Z N)
Съгласно полученото уравнение еквивалентната схема за нулевата последователност ще приеме формата (фиг. 43.2 c), в която тройно неутралното съпротивление 3Z N е включено последователно с фазовото съпротивление Z 0 .
В схемите за отделни симетрични компоненти (фиг. 43.2 a, b, c) са посочени Z 1, Z 2, Z 0 - комплексните съпротивления на фазата на приемника за токове съответно на постоянна, отрицателна и нулева последователност. За приемници с въртящо се магнитно поле тези съпротивления са значително различни.
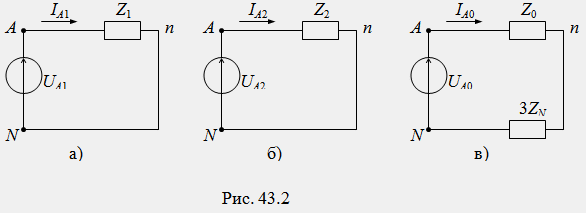
Съгласно закона на Ом във всяка от веригите на фиг. 43.2a, b, c се изчисляват токовете на постоянна, отрицателна и нулева последователност:
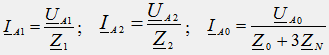
Действителните токове в оригиналната верига (фиг. 43.1) се определят с помощта на метода на суперпозиция, като векторни суми на токове с права, отрицателна и нулева последователност:
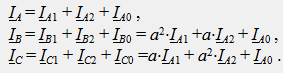
Комплексните фазови съпротивления на статични трифазни приемници (осветителни товари, нагревателни устройства и др.) Не зависят от вида на последователността, за такива приемници Z 1 = Z 2 = Z 0 . Токовете на такива приемници могат да бъдат изчислени с помощта на конвенционални методи. За трифазни приемници, в които има въртящо се магнитно поле (електродвигатели, генератори), фазовите съпротивления за токове от различни последователности се различават значително (Z 1 > Z 0 > Z 2). Изчисляването на токовете на такива приемници при асиметрично напрежение трябва да се извършва изключително по метода на симетричните компоненти.
Разглежда се за случая с работещ неутрален проводник. Векторни диаграми на напрежения и токове са дадени на фигури 15 и 16; Фигура 17 показва комбинирана диаграма на токове и напрежения
1. Построени са осите на комплексната равнина: реални величини (+1) - хоризонтално, имагинерни величини (j) - вертикално.
2. Въз основа на стойностите на модулите за ток и напрежение и размера на полетата на листа, разпределени за конструиране на диаграми, се избират скалите на тока mI и напрежението mU. При използване на формат А4 (размери 210x297 mm) с най-големите модули (вижте таблица 8) ток 54 A и напрежение 433 V се приемат следните скали: mI = 5 A/cm, mU = 50 V/cm.
3. Като се вземат предвид приетите скали mI и mU, дължината на всеки вектор се определя, ако диаграмата е конструирана с помощта на експоненциалната форма на нейното обозначение; при използване на алгебричната форма се намират дължините на проекциите на вектори върху осите на реални и имагинерни величини, т.е. дължините на реалните и въображаемите части на комплекса.
Например за фаза А:
Дължина на вектора на тока / f.A / = 34,8 A / 5 A/cm = 6,96 cm; дължината на реалната му част
I f.A = 30 A/ 5 A/cm = 6 cm,
дължината на въображаемата му част
I f.A = -17,8 A/5 A/cm = - 3,56 cm;
Дължина на вектора на напрежение / A товар / = 348 V / 50 V/cm = 6,96 cm; дължината на реалната му част
U Натоварване = 340,5 V/ 50 V/cm = 6,8 cm;
дължината на въображаемата му част
U Anagr. = 37,75 V/ 50 V/cm = 0,76 cm.
Резултатите от определянето на дължините на векторите, техните реални и въображаеми части са отразени в таблица 9.
Таблица 9 - Дължини на векторите на тока и напрежението, техните реални и въображаеми части за случай на непокътнат неутрален проводник.
| величина | Мащаб, 1/см | Дължина на вектора, cm | Дължина на реалната част, cm | Дължина на въображаемата част, cm | |
| Мрежови фазови напрежения | U A | 50 V/cm | 7,6 | 7,6 | |
| UВ | 7,6 | - 3,8 | - 6,56 | ||
| UС | 7,6 | - 3,8 | 6,56 | ||
| Фазови напрежения на товара | U Anagr. | 50 V/cm | 6,96 | 6,8 | 0,76 |
| UV натоварване | 7,4 | - 4,59 | - 5,8 | ||
| UС отопление | 8,66 | -4,59 | 7,32 | ||
| U0 | 1,08 | 0,79 | - 0,76 |
Продължение на таблица 9
| Фазови токове на натоварване | Ако | 5 A/см | 6,96 | 6.0 | - 3,56 |
| аз f.b | 7,4 | 1,87 | - 7,14 | ||
| I f.S | 3,13 | 0,1 | 3,12 | ||
| аз 0 | 10,8 | 7,9 | - 7,6 |
4. Построяване на векторна диаграма на напрежението.
4.1 В комплексната равнина са построени векторите на фазовото напрежение на захранващата мрежа A, B, C; свързвайки краищата им, получаваме векторите линейни напрежения AB, BC, SA. След това се конструират векторите на фазовото напрежение на товара A товар, B товар, C товар. За да ги конструирате, можете да използвате и двете форми на запис на комплекси от токове и напрежения.
Точка 0, където ще бъдат техните начала, е неутрален товар. В тази точка е краят на вектора на напрежението на неутралното изместване 0, началото му се намира в точка 0. Този вектор може да бъде конструиран и с помощта на данните в таблица 9.
5. Построяване на векторна диаграма на токовете.
5.1 Конструкцията на векторите на фазовия ток f.A, f.B, f.C е подобна на конструкцията на векторите на фазовото напрежение.
5.2 Чрез добавяне на векторите на фазовия ток се намира векторът на тока в нулевия проводник 0; неговата дължина и дължините на неговите проекции върху оста трябва да съвпадат с тези, посочени в таблица 8.
По подобен начин се изграждат векторни диаграми на токове и напрежения за случай на счупен неутрален проводник.
Необходимо е да се анализират резултатите от изчислението и изграждането на векторни диаграми и да се направят изводи за влиянието на асиметрията на товара върху величината на неговите фазови напрежения и върху неутралното напрежение; Специално вниманиее необходимо да се обърне внимание на последствията от прекъсване на нулевия проводник на мрежата по време на асиметрично натоварване.
Забележка. Допуска се комбиниране на диаграми на ток и напрежение, при условие че са изпълнени в различни цветове.
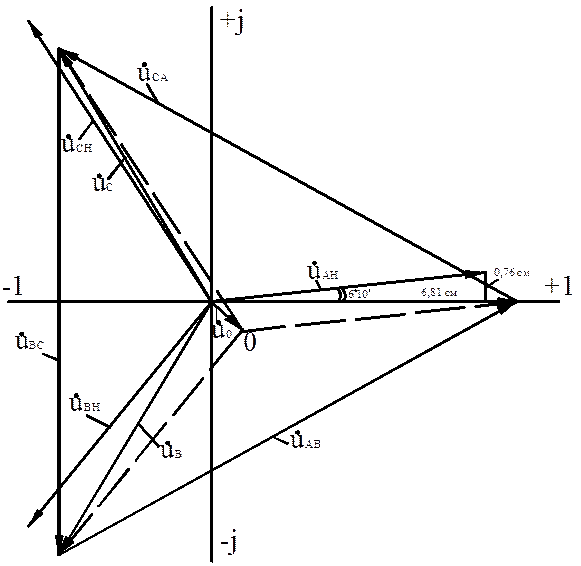
Фигура 15. Векторна диаграма на напрежението
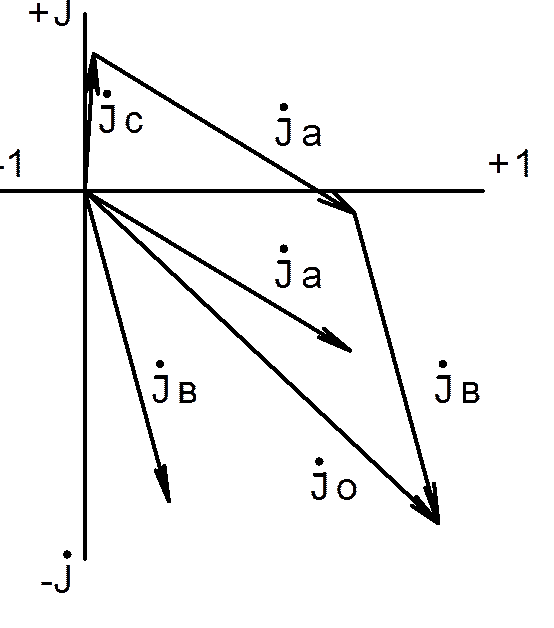
Фигура 16. Векторна диаграма на токовете.

Фигура 17. Комбинирана векторна диаграма на напрежения и токове.