How to build a vector diagram. Building vector diagrams

Problem 6.1. In the circuit shown in Fig. 6.1, the voltages across the active resistance were measured U R and on coil terminals U K, and also the angle φ between voltage Ū K and current Ī .

The measurements gave the following results: U R = 100 V, U K = 120 V, φ =75º.

It is required to determine the value of the input voltage U .

We build a vector diagram of a given circuit (Fig. 6.2).

Since the circuit is unbranched, we start the construction with the current vector Ī . Draw a vector along it Ū R and add the vector to it Ū K , leading current per angle φ . Sum of vectors Ū R and Ū K gives the input voltage vector Ū , the length of which determines the value of the input voltage, we find by the cosine theorem:

Problem 6.2. In the circuit in Fig. 6.3 resonance.

Find the current value I 3 if U = 80 V, I 2 = 4 A, R = 25 Ohm.

The problem is easily solved using a vector diagram. Since the resonance in the circuit, the voltage and current at the input of the circuit are in phase, the vectors Ū And Ī 1 are directed in one direction (Fig. 6.4). The voltage in the first section lags behind the current Ī 1 at 90º. Vector Ū 1 is directed perpendicularly down. Vector Ū 2 draw from the end of the vector Ū 1 to end of vector Ū - so that the equality is fulfilled: Ū 1 + Ū 2 = Ū . Current Ī 2 is in phase with voltage Ū 2 , and Ī 3 lags behind it by 90º. In sum, they give current Ī 1 .

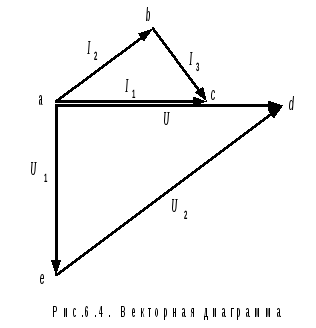
According to Ohm's law for the second branch:

From a triangle ade :

From the similarity of triangles abc And ade follows:

We calculate:

Problem 6.3. To coil with parameters R And L capacitance connected in parallel C (Figure 6.5, a). It is known that the resonance in the circuit and the values ​​​​of two currents are given: I To= 5 A and I \u003d 3 A. What is the capacitance of the capacitor if the value of the supply voltage U = 220 V, and its frequency f = 50 Hz?

The vector diagram quickly leads to the result (Fig. 6.5, b).

Current Ī to undervoltage Ū at some angle, current Ī c leads the voltage by 90º. The sum of these two currents gives the total current: Ī = Ī to + Ī With. Since there is resonance in the circuit, the total current vector is directed along the voltage vector.

The current diagram is a right triangle, from which it follows:

Capacitance

and the capacitance of the capacitor

CONCLUSION

Vector diagram gives full information about the electrical circuit. You can even say that it is one of the ways to represent an electrical circuit - its configuration allows you to determine the structure of the circuit. And if it is built on a scale, it gives the numerical values ​​​​of voltages and currents on all elements of the circuit, and also allows you to find the values ​​​​of all resistances.

CONTROL QUESTIONS

1. What is a vector? How are current and voltage vectors indicated in an electrical circuit?

2. What rules of vector addition do you know?

3. How are the current and voltage vectors directed relative to each other in active resistance, inductance and capacitance?

4. What laws of the electrical circuit are used in the construction of vector diagrams?

5. From which vector is it advisable to start building a vector diagram?

6. In what sequence should vectors be plotted when plotting a diagram?

CONTROL TASKS

In the diagram given by the teacher, designate voltages and currents in all sections and build a vector diagram.

REFERENCES

1. Theoretical foundations of electrical engineering: in 3 volumes. Textbook for universities. Volume 1. - 4th ed. / K.S. Demirchyan, L.R. Neiman, N.V. Korovin, V.L. Chechurin. - St. Petersburg: Peter, 2004, - 463 p.: ill.

REFERENCES

1. Theoretical foundations of electrical engineering: in 3 volumes. Textbook for universities. Volume 1. - 4th ed. / K.S. Demargyan, L.R. Neiman, N.V. Korovin, V.L. Chechurin. - St. Petersburg: Peter, 2004, - 463 p.: ill.

2. Matyushchenko V.S. Theoretical foundations of electrical engineering. Linear electrical circuits of direct and single-phase sinusoidal currents: textbook. allowance / V.S. Matyushchenko. - Khabarovsk. - Khabarovsk: Publishing House of the Far East State University of Transportation, 2002. - 112 p.

3. Matyushchenko V.S. Calculation of complex electrical circuits of direct and sinusoidal currents: textbook. allowance / V.S. Matyushchenko. - Khabarovsk: Publishing House of the Far East State University of Transportation, 2004. - 69 p.

Task 3

The current vector is built first, then the voltage vectors.

Task 4
Build a high-quality vector diagram.
The construction is carried out using the properties of the elements.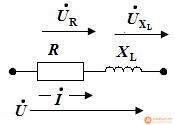

Task 5
Build a quality vector diagram for the circuit, provided that XL>XC.
The construction is carried out using the properties of the elements.

Task

IN serial circuit determine instrument readings, compile and calculate the power balance, determine the power factor, build a topographic vector diagram.

R1 = 10 ohm
R2 = 20 ohm
C = 31.8uF
L = 0.127 H
f = 50 Hz

1). Let us determine the total complex resistances of reactive elements

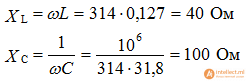
2). Let's translate the source voltage into algebraic form

3). Determine the equivalent resistance of the circuit

The circuit has an active-capacitive character

4). Determine the current in the circuit

5). The ammeter will show effective value current

6). Determine the voltmeter reading, the effective value of the voltage across the capacitor

7). Determine the power of the source and receivers

Receiver Power

It can be seen from the calculations that the balance converges with an error of less than a percent.

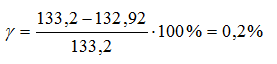
8). Determine the power factor

9) building a topographic vector diagram
Determine the voltage on the circuit elements

Current scale selection 2 cm - 1 A; voltage 2cm - 50 V
The rule for constructing a vector diagram, with the sequential inclusion of elements:
build the current vector
build stress vectors
add the stress vectors according to the parallelogram rule.

Basically, vector diagrams are built on the complex plane and

are of two types:- vector diagrams of currents and voltages;

- vector topographic stress diagrams.

All vector diagrams plotted to scale for both currents and voltages. The coordinate axes are denoted on the complex plane +1 And +j. The diagramming technique depends on the electrical circuit connection scheme. If the circuit elements R, L, C are connected in series, then the "reference" in the diagram is the current vector, as common to all elements. Next, voltage vectors are built taking into account the phase shift between the current and voltages on the elements (see diagram A). The geometric sum of the voltage vectors must be equal to the voltage vector applied to the electrical circuit.

Diagram A Diagram B

If the circuit elements R, L, C are connected in parallel, then the "reference" in the diagram is the voltage vector, as common to all elements. Next, current vectors are constructed taking into account the phase shift between voltage and currents in the branches of the circuit (see diagram B). The geometric sum of the current vectors in the branches must be equal to the total current in the electric circuit.

Topographic stress diagram is a diagram of the complex potentials of the points of an electrical circuit, laid out in a certain order. The potential of one of the points is taken equal to zero, and then two construction options are possible: the first is that the potentials of the remaining points are calculated relative to this potential; the second - from this point, the voltage modules on the elements with the corresponding phase shift angles are plotted. The order of constructing a topographic diagram is visible on simple example(see Diagram B and Diagram B).

Diagram B Diagram B

IN electrical circuits with a mixed connection of elements, a topographic stress diagram is usually built in several stages. In this case, diagrams are first constructed for individual circuit branches, which implies the presence of a vector current diagram for the entire circuit, and then combined into a common topographic diagram.

End of work -