İntegraller, parçalara göre bir entegrasyon yöntemidir. Kesin integral. Çözüm örnekleri
Belirli bir X aralığında türevlenebilen bir F(x) fonksiyonuna denir. fonksiyon için ters türev f(x) veya herhangi bir x ∈X için eşitlik geçerliyse f(x)'in bir integrali:
F "(x) = f(x).(8.1)
Belirli bir işlev için tüm ters türevleri bulmaya onun adı verilir. entegrasyon. Fonksiyonun belirsiz integrali Belirli bir X aralığında f(x) f(x) fonksiyonu için tüm ters türevlerin kümesidir; atama -
Eğer F(x), f(x) fonksiyonu için bir ters türev ise, o zaman ∫ f(x)dx = F(x) + C, (8.2)
burada C keyfi bir sabittir.
İntegral tablosu
Doğrudan tanımdan, belirsiz integralin ana özelliklerini ve tablo integrallerinin listesini elde ederiz:
1) d∫f(x)dx=f(x)
2)∫df(x)=f(x)+C
3) ∫af(x)dx=a∫f(x)dx (a=sabit)
4) ∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx
Tablo integrallerinin listesi
1. ∫x m dx = x m+1 /(m + 1) +C; (m ≠ -1)
3.∫a x dx = a x / ln a + C (a>0, a ≠1)
4.∫e x dx = e x + C
5.∫sin x dx = cosx + C
6.∫cos x dx = - sin x + C
7. = yay x + C
8.=arksin x + C
10.=-ctg x + C
Değişken ikamesi
Birçok işlevi entegre etmek için bir değişkeni değiştirme yöntemi kullanılır veya ikameler, integralleri bir tablo formuna getirmeye izin verir.
f(z) fonksiyonu [α,β] üzerinde sürekliyse, z =g(x) fonksiyonunun sürekli bir türevi vardır ve α ≤ g(x) ≤ β'dır, o zaman
∫ f(g(x)) g " (x) dx = ∫f(z)dz, (8.3)
ayrıca sağ taraftaki integral alındıktan sonra z=g(x) yerine yazılmalıdır.
Bunu kanıtlamak için orijinal integrali şu şekilde yazmak yeterlidir:
∫ f(g(x)) g " (x) dx = ∫ f(g(x)) dg(x).
Örneğin:
Parçalara göre entegrasyon yöntemi
u = f(x) ve v = g(x) sürekli olan fonksiyonlar olsun. Daha sonra eserlere göre;
d(uv))= udv + vdu veya udv = d(uv) - vdu.
d(uv) ifadesi için, ters türev açıkça uv olacaktır, bu nedenle formül gerçekleşir:
∫ udv = uv - ∫ vdu (8.4.)
Bu formül kuralı ifade eder Parçalara göre entegrasyon. udv=uv"dx ifadesinin entegrasyonunu vdu=vu"dx ifadesinin entegrasyonuna getirir.
Örneğin, ∫xcosx dx'i bulmak gerekiyor. u = x, dv = cosxdx olsun, yani du=dx, v=sinx. Daha sonra
∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.
Parçalara göre entegrasyon kuralı, değişken değişikliğinden daha sınırlı bir kapsama sahiptir. Ancak bütün integral sınıfları vardır, örneğin,
∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax ve diğerleri, tam olarak parçalara göre entegrasyon kullanılarak hesaplanır.
Kesin integral
Belirli bir integral kavramı aşağıdaki gibi tanıtılmaktadır. Bir f(x) fonksiyonu bir aralıkta tanımlansın. [a,b] segmentini ikiye ayıralım N noktalara göre parçalar a= x 0< x 1 <...< x n = b. Из каждого интервала (x i-1 ,
x i) возьмем произвольную точку ξ i и составим сумму f(ξ i)
Δx i где
Δ x ben \u003d x ben - x ben-1. f(ξ i)Δ x i formunun toplamına denir integral toplamλ = maxΔx i → 0'daki limiti, eğer varsa ve sonlu ise, denir kesin integral f(x) fonksiyonları Aönce B ve şu şekilde gösterilir:
F(ξi)Δxi (8.5).
Bu durumda f(x) fonksiyonuna denir bir segment üzerinde entegre edilebilir, a ve b sayıları çağrılır integralin alt ve üst limiti.
Belirli bir integral için aşağıdaki özellikler geçerlidir:
4), (k = sabit, k∈R);
5)![]()
6)![]()
7) f(ξ)(b-a) (ξ∈).
Son özellik denir ortalama değer teoremi.
f(x) üzerinde sürekli olsun. O halde bu doğru parçasında belirsiz bir integral vardır.
∫f(x)dx = F(x) + C
ve gerçekleşir Newton-Leibniz formülü, belirli integrali belirsiz olana bağlayan:
F(b) - F(a). (8.6)
Geometrik yorum: belirli integral, y=f(x) eğrisi, x = a ve x = b düz çizgileri ve eksen parçası tarafından yukarıdan sınırlanan eğrisel bir yamuğun alanıdır. Öküz.
uygun olmayan integraller
Sonsuz limitli integraller ve süreksiz (sınırsız) fonksiyonların integrallerine denir. uygunsuz. Birinci türden uygun olmayan integraller - bunlar, aşağıdaki gibi tanımlanan sonsuz bir aralıktaki integrallerdir:
![]() (8.7)
(8.7)
Bu limit varsa ve sonlu ise, buna denir. f(x)'in yakınsak uygun olmayan integrali[а,+ ∞) aralığında ve f(x) işlevi çağrılır sonsuz bir aralıkta integrallenebilir[a,+ ∞). Aksi takdirde, integral olduğu söylenir mevcut değil veya farklılaşıyor.
(-∞,b] ve (-∞, + ∞) aralıklarındaki uygunsuz integraller benzer şekilde tanımlanır:
Sınırsız bir fonksiyonun integral kavramını tanımlayalım. f(x) tüm değerler için sürekli ise X f(x)'in sonsuz süreksizliğe sahip olduğu c noktası hariç segment , o zaman ikinci türden uygunsuz integral f(x) a'dan b'ye kadar toplamı denir:
![]()
eğer bu sınırlar varsa ve sonluysa. tanım:
İntegral hesaplama örnekleri
Örnek 3.30.∫dx/(x+2) hesaplayın.
Çözüm. t = x+2, sonra dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| +C.
Örnek 3.31. ∫ tgxdx'i bulun.
Çözüm.∫tgxdx = ∫sinx/cosxdx = - ∫dcosx/cosx. t=cosx olsun, o zaman ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.
Örnek3.32 . ∫dx/sinx'i bulunÇözüm.
Örnek3.33. Bulmak .
Çözüm. = .
Örnek3.34 . ∫arctgxdx'i bulun.
Çözüm. Parçalara göre entegre ediyoruz. u=arctgx, dv=dx'i belirtin. O halde du = dx/(x 2 +1), v=x, buradan ∫yaygxdx = xyaygx - ∫ xdx/(x 2 +1) = xyaygx + 1/2 ln(x 2 +1) +C; Çünkü
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.
Örnek3.35 . ∫lnxdx'i hesaplayın.
Çözüm. Parçalara göre entegrasyon formülünü uygulayarak şunu elde ederiz:
u=lnx, dv=dx, du=1/x dx, v=x. O halde ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.
Örnek3.36 . ∫e x sinxdx'i hesaplayın.
Çözüm. u = e x , dv = sinxdx, sonra du = e x dx, v =∫sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx'i belirtin. ∫e x cosxdx integrali ayrıca şu kısımlarda da integrallenebilir: u = e x , dv = cosxdx, du=e x dx, v=sinx. Sahibiz:
∫ e x cosxdx = e x sinx - ∫ e x sinxdx. ∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx bağıntısını elde ettik, dolayısıyla 2∫e x sinx dx = - e x cosx + e x sinx + C.
Örnek 3.37. J = ∫cos(lnx)dx/x'i hesaplayın.
Çözüm. dx/x = dlnx olduğundan, J= ∫cos(lnx)d(lnx). lnx'i t ile değiştirerek, J = ∫ costdt = sint + C = sin(lnx) + C tablosuna ulaşırız.
Örnek 3.38 . J = hesaplayın.
Çözüm.= d(lnx) olduğunu hesaba katarak, lnx = t ikamesini yaparız. O zaman J = ![]() .
.
Örnek 3.39
. J = integralini hesaplayın ![]() .
.
Çözüm. Sahibiz: ![]() . Bu nedenle =
. Bu nedenle =
=
=. sqrt(tan(x/2)) olarak girilir.
Ve sonuç penceresinde sağ üst köşedeki Adımları göster'e tıklarsanız, ayrıntılı bir çözüm elde edersiniz.
Parçalara göre entegrasyon nedir? Bu tür bir entegrasyonda ustalaşmak için önce çarpımın türevini hatırlayalım:
$((\left(f\cdot g \sağ))^(\prime ))=(f)"\cdot g+f\cdot (g)"$
Soru şu: Peki, integrallerin bununla ne ilgisi var? Şimdi bu denklemin iki tarafını da entegre edelim. Öyleyse yazalım:
$\int(((\left(f\cdot g \sağ))^(\prime ))\text(d)x=)\int((f)"\cdot g\,\text(d)x+\int(f\cdot (g)"\,\text(d)x))$
Ama bir inmenin ilkelliği nedir? Bu sadece vuruşun içindeki işlevin kendisidir. Öyleyse yazalım:
$f\cdot g=\int((f)"\cdot g\,\text(d)x+\int(f\cdot (g)"\,\text(d)x))$
Bu denklemde, terimi ifade etmeyi öneriyorum. Sahibiz:
$\int((f)"\cdot g\,\text(d)x=f\cdot g-\int(f\cdot (g)"\,\text(d)x))$
işte bu parçalara göre entegrasyon formülü. Yani esasen türevi ve fonksiyonu değiştiriyoruz. Başlangıçta vuruşun integralini bir şeyle çarpmış olsaydık, o zaman yeni bir şeyin integralini vuruşla çarpardık. Tüm kural bu. İlk bakışta, bu formül karmaşık ve anlamsız görünebilir, ancak aslında hesaplamaları büyük ölçüde basitleştirebilir. Görelim.
İntegral hesaplama örnekleri
Görev 1. Hesaplayın:
\[\int(\ln x\,\text(d)x)\]\[\]
Logaritmanın önüne 1 ekleyerek ifadeyi yeniden yazalım:
\[\int(\ln x\,\text(d)x)=\int(1\cdot \ln x\,\text(d)x)\]
Bunu yapmaya hakkımız var çünkü ne sayı ne de fonksiyon değişmeyecek. Şimdi bu ifadeyi formülde yazdıklarımızla karşılaştıralım. $(f)"$'nin rolü 1'dir, dolayısıyla şunu yazıyoruz:
$\begin(align)& (f)"=1\Rightarrow f=x \\& g=\ln x\Rightarrow (g)"=\frac(1)(x) \\\end(align)$
Tüm bu işlevler tablolardadır. Artık ifademizde yer alan tüm elemanları yazdığımıza göre, bu integrali kısmi entegrasyon formülüne göre yeniden yazacağız:
\[\begin(align)& \int(1\cdot \ln x\,\text(d)x)=x\ln x-\int(x\cdot \frac(1)(x)\text(d)x)=x\ln x-\int(\text(d)x)= \\& =x\ln x-x+C=x\left(\ln x-1 \right)+C \\\end(align)\ ]
İşte bu, integral bulundu.
Görev 2. Hesaplayın:
$\int(x((\text(e))^(-x))\,\text(d)x=\int(x\cdot ((e)^(-x))\,\text(d)x))$
Şimdi ters türevi bulmamız gereken türev olarak $x$ alırsak, $((x)^(2))$ elde ederiz ve son ifade $((x)^(2))((\text(e))^(-x))$ içerecektir.
Açıkçası, görev basitleştirilmemiş, bu yüzden integral işareti altındaki faktörleri değiştireceğiz:
$\int(x\cdot ((\text(e))^(-x))\,\text(d)x)=\int(((\text(e))^(-x))\cdot x\,\text(d)x)$
Şimdi notasyonu tanıtalım:
$(f)"=((\text(e))^(-x))\Rightarrow f=\int(((\text(e))^(-x))\,\text(d)x)=-((\text(e))^(-x))$
$((\text(e))^(-x))$'yi ayırt edin:
$((\left(((\text(e))^(-x)) \sağ))^(\prime ))=((\text(e))^(-x))\cdot ((\left(-x \sağ))^(\prime ))=-((\text(e))^(-x))$
Başka bir deyişle, önce "eksi" eklenir ve ardından her iki taraf da entegre edilir:
\[\begin(hizala)& ((\left(((\text(e))^(-x)) \right))^(\prime ))=-((\text(e))^(-x))\Rightarrow ((\text(e))^(-x))=-((\left(((\text(e))^(-x)) \sağ))^(\prime )) \\& \int(((\text(e))^(-x))\,\text( d) x)=-\int(((\left(((\text(e))^(-x)) \sağ))^(\prime ))\text(d)x)=-((\text(e))^(-x))+C \\\end(hizala)\]
Şimdi $g$ işleviyle ilgilenelim:
$g=x\Sağ ok (g)"=1$
İntegrali ele alıyoruz:
$\begin(align)& \int(((\text(e))^(-x))\cdot x\,\text(d)x)=x\cdot \left(-((\text(e))^(-x)) \right)-\int(\left(-((\text(e))^(-x)) \right)\cdot 1\cdot \text(d)x)= \\& =-x((\text(e))^ (-x ))+\int(((\text(e))^(-x))\,\text(d)x)=-x((\text(e))^(-x))-((\text(e))^(-x))+C=-((\text(e))^(-x))\left(x+1 \right)+C \\\end(align)$
Böylece ikinci entegrasyonu parça parça gerçekleştirmiş olduk.
Görev 3. Hesaplayın:
$\int(x\cos 3x\,\text(d)x)$
Bu durumda $(f)"$ için ne almalı ve $g$ için ne almalı? $x$ bir türev görevi görürse, entegrasyon sırasında $\frac(((x)^(2)))(2)$ görünecektir ve ilk çarpan hiçbir yerde kaybolmayacaktır - $\frac(((x)^(2)))(2)\cdot \cos 3x$ olacaktır. Bu nedenle, faktörleri yeniden değiştireceğiz:
$\begin(align)& \int(x\cos 3x\,\text(d)x)=\int(\cos 3x\cdot x\,\text(d)x) \\& (f)"=\cos 3x\Rightarrow f=\int(\cos 3x\,\text(d)x)=\frac(\sin 3x)(3) \\& g=x\Rightarrow (g)"= 1 \\ \end(hizala)$
Orijinal ifademizi yeniden yazıyoruz ve parçalara göre entegrasyon formülüne göre genişletiyoruz:
\[\begin(align)& \int(\cos 3x\cdot x\ \text(d)x)=\frac(\sin 3x)(3)\cdot x-\int(\frac(\sin 3x)(3)\text(d)x)= \\& =\frac(x\sin 3x)(3)-\frac(1)(3)\int(\sin 3x\,\text(d) x)=\frac(x\sin 3x)(3)+\frac(\cos 3x)(9)+C \\\end(hizala)\]
Her şey, üçüncü görev çözüldü.
Son olarak tekrar bakalım parçalara göre entegrasyon formülü. Faktörlerden hangisinin türev, hangisinin gerçek fonksiyon olacağını nasıl seçeriz? Burada tek bir kriter vardır: Farklılaştıracağımız öğe ya "güzel" bir ifade vermeli ve bu ifade küçülmeli ya da farklılaşma sırasında tamamen kaybolmalıdır. Bu ders bitti.
Aşağıdaki formül denir parça formülü ile entegrasyon belirsiz bir integralde:
Parçalara göre entegrasyon formülünü uygulamak için, integralin iki faktöre bölünmesi gerekir. Bunlardan biri ile gösterilir sen, ve geri kalanı ikinci faktörü ifade eder ve ile gösterilir dv. Sonra türev alarak buluruz du ve entegrasyon - fonksiyon v. için aynı zamanda sen dv- entegrenin kolayca entegre edilebilecek kısmı.
Parçalara göre entegrasyon yöntemini kullanmak ne zaman avantajlıdır? Sonra ne zaman entegre içerir :
1) - logaritmik fonksiyonlar ve ayrıca ters trigonometrik fonksiyonlar ("yay" ön ekiyle), daha sonra, parçalarla uzun bir entegrasyon deneyimine dayanarak, bu fonksiyonlar şu şekilde gösterilir: sen;
2) , , - sinüs, kosinüs ve üs ile çarpılan P(X) x'te isteğe bağlı bir polinomdur, o zaman bu fonksiyonlar şu şekilde gösterilir: dv ve polinom - aracılığıyla sen;
3) , , , , bu durumda kısmi integral iki kez uygulanır.
İntegrasyon yönteminin değerini parçalara göre birinci durum örneğini kullanarak açıklayalım. İntegral işareti altındaki ifade logaritmik bir fonksiyon içersin (bu örnek 1 olacak). Parçalara göre entegrasyon kullanılarak, böyle bir integral, yalnızca cebirsel işlevlerin (çoğunlukla bir polinom), yani logaritmik veya ters trigonometrik bir işlev içermeyen integralinin hesaplanmasına indirgenir. Dersin başında verilen parçalara göre integral alma formülünün uygulanması
ilk terimde (integral olmadan) bir logaritmik fonksiyon ve ikinci terimde (integral işareti altında) - logaritma içermeyen bir fonksiyon elde ederiz. Bir cebirsel fonksiyonun integrali, altında tek başına veya cebirsel bir çarpanla birlikte logaritmik veya ters trigonometrik bir fonksiyonun bulunduğu bir integralden çok daha basittir.
Böylece yardım ile parçalara göre entegrasyon formülleri entegrasyon hemen yapılmaz: belirli bir integrali bulmak, başka bir integrali bulmaya indirgenir. Parçalara göre entegrasyon formülünün anlamı, uygulanmasının bir sonucu olarak, yeni integralin tablo şeklinde çıkması veya en azından orijinalinden daha basit hale gelmesidir.
Parçalara göre entegrasyon yöntemi, iki işlevin ürününü farklılaştırmak için formülün kullanımına dayanır:
şeklinde yazılabilir.
dersin en başında verildi.
Fonksiyonu entegre ederek bulurken v bunun için sonsuz bir ters türevli fonksiyonlar kümesi elde edilir. Parçalara göre entegrasyon formülünü uygulamak için bunlardan herhangi birini ve dolayısıyla keyfi bir sabite karşılık gelen olanı alabilirsiniz. İLE sıfıra eşittir. Bu nedenle, işlevi bulurken v keyfi sabit İLE girilmemelidir.
Parçalara göre entegrasyon yönteminin çok özel bir uygulaması vardır: İntegral işareti altındaki fonksiyonların derecesini düşürmek gerektiğinde ters türevleri bulmak için özyinelemeli formüller türetmek için kullanılabilir. Sinüs ve kosinüs gibi ikiden büyük bir güce sahip fonksiyonlar ve bunların çarpımı için tablo integralleri olmadığında derece indirgeme gereklidir. Özyinelemeli bir formül, bir dizinin bir sonraki üyesini önceki üye cinsinden bulmak için kullanılan bir formüldür. Belirtilen durumlarda, hedefe, derecenin art arda düşürülmesiyle ulaşılır. İntegrand, sinüs üzeri x'in dördüncü kuvveti ise, o zaman parçalara göre integral alarak sinüsün üçüncü kuvvetine göre integrali için bir formül bulabilirsiniz, vb. Bu dersin son paragrafı açıklanan soruna ayrılmıştır.
Parçalara göre entegrasyonu birlikte uygulama
Örnek 1. Parçalara göre integral alarak belirsiz integrali bulun:
Çözüm. İntegrand'da, zaten bildiğimiz gibi makul bir şekilde şu şekilde gösterilebilen logaritma: sen. Sanıyoruz ki , .
Şunu buluruz (teorik referansın açıklamasında daha önce bahsedildiği gibi, hemen birinci terimde (integral olmadan) bir logaritmik fonksiyon ve ikinci terimde (integral işareti altında) logaritmayı içermeyen bir fonksiyon elde ederiz:

Ve yine logaritma...
Örnek 2 Belirsiz integrali bulun:
Çözüm. İzin vermek , .
Logaritma karede bulunur. Bu, karmaşık bir fonksiyon olarak ayırt edilmesi gerektiği anlamına gelir. Bulduk
,
.

İkinci integrali parça parça buluyoruz ve daha önce bahsedilen avantajı elde ediyoruz (ilk terimde (integral olmadan) logaritmik bir fonksiyon ve ikinci terimde (integral işareti altında) - logaritma içermeyen bir fonksiyon).


Orijinal integrali buluyoruz:

Örnek 3
Çözüm. Ark teğeti, logaritma gibi en iyi şu şekilde gösterilir: sen. Öyleyse izin ver .
Daha sonra ,
.
Parçalara göre entegrasyon formülünü uygulayarak şunu elde ederiz:
![]()
İkinci integral, değişken yönteminin değiştirilmesiyle bulunur.


değişkene dönüş X, alırız
![]() .
.
Orijinal integrali buluyoruz:
![]() .
.
Örnek 4. Parçalara göre integral alarak belirsiz integrali bulun:
Çözüm. Üs daha iyi şu şekilde gösterilir: dv. İntegrandı iki faktöre ayırdık. varsayarsak
Örnek 5. Parçalara Göre İntegral Kullanarak Belirsiz İntegrali Bulun:
![]() .
.
Çözüm. İzin vermek , . Daha sonra , .
Parçalara göre entegrasyon formülünü (1) kullanarak şunu buluruz:

Örnek 6 Parçalara göre integral alarak belirsiz integrali bulun:
Çözüm. Üs gibi sinüs de rahatlıkla şu şekilde gösterilebilir: dv. İzin vermek , .
Parçalara göre entegrasyon formülünü kullanarak şunu buluruz:
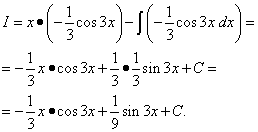
Parçalara göre entegrasyonu tekrar birlikte uygulamak
Örnek 10 Parçalara göre integral alarak belirsiz integrali bulun:
![]() .
.
Çözüm. Tüm benzer durumlarda olduğu gibi, kosinüs uygun şekilde şu şekilde gösterilir: dv. , .
Daha sonra ![]() ,
.
,
.
Parçalara göre entegrasyon formülünü kullanarak şunu elde ederiz:
İkinci terime kısmi integral de uyguluyoruz. , .
Bu gösterimleri uygulayarak, belirtilen terimi entegre ediyoruz:

Şimdi gerekli integrali buluyoruz:

Parçalara göre entegrasyon yöntemiyle çözülebilen integraller arasında, teorik bölümde belirtilen üç gruptan hiçbirine dahil olmayanlar vardır ve bunlar için pratikten şu şekilde göstermenin daha iyi olduğu bilinmektedir: sen ve ne yoluyla dv. Bu nedenle, bu durumlarda, "Kısmen entegrasyon yönteminin özü" paragrafında da verilen uygunluk değerlendirmesini kullanmak gerekir: sen integrand'ın öyle bir kısmı alınmalıdır ki, farklılaşma sırasında çok daha karmaşık hale gelmez, ancak dv- entegrenin kolayca entegre edilebilecek kısmı. Bu dersin son örneği, böyle bir integralin çözümüdür.
Ters türev ve belirsiz integral kavramı. Ters türevlerin toplanmasına ilişkin teorem. Belirsiz integralin özellikleri. İntegral tablosu.
F(x) işlevi bu aralıkta sürekliyse ve eşitlik aralığın her iç noktasında doğruysa, F(x) işlevi belirli bir aralıkta f(x) işlevinin ters türevi olarak adlandırılır: F’(x) = f(x)
teorem 1. Bir F(x) fonksiyonunun bir aralıkta F(x) ters türevi varsa, o zaman F(x)+C formunun tüm fonksiyonları aynı aralıkta onun için ters türev olacaktır. Tersine, y = f(x) fonksiyonu için herhangi bir ters türev Ф(x), Ф(x) = F(x)+C olarak temsil edilebilir, burada F(x) ters türevlerden biridir ve C keyfi bir sabittir.
Kanıt:
Ters türevin tanımı gereği, elimizde F'(x) = f(x) var. Sabitin türevinin sıfıra eşit olduğunu düşünürsek,
(F(x)+C)' = F'(x)+C' = F'(x) = f(x). Bu, F(x)+C'nin y = f(x) için bir terstürev olduğu anlamına gelir.Şimdi bir y = f(x) fonksiyonu belirli bir aralıkta tanımlanmışsa ve F(x) onun terstürevlerinden biriyse, o zaman Ф(x)'in şu şekilde temsil edilebileceğini gösterelim:
Aslında, bir ters türevin tanımı gereği, elimizde
F'(x) = F(x)+C ve F'(x) = f(x).
Ancak aralıkta eşit türevlere sahip iki fonksiyon birbirinden yalnızca sabit bir terim kadar farklıdır. Dolayısıyla, kanıtlanması gereken Ф(x) = F(x) + C.
Tanım.
Belirli bir aralıktaki bir y = f(x) fonksiyonu için tüm ters türevlerin kümesine bu fonksiyonun belirsiz integrali denir ve ∫f(x)dx = F(x)+C ile gösterilir.
f(x) fonksiyonuna integral denir ve f(x)*dx ürününe integral denir.
Sık sık şöyle söylenir: "belirsiz integrali al" veya "belirsiz integrali hesapla", bununla şu anlama gelir: integral için tüm ters türevlerin kümesini bul,
belirsiz integralin özellikleri
1. (f(x)dx) = f(x)
2. ∫f′(x)dx = f(x) + c
3. ∫a ⋅ f(x)dx = a∫f(x)dx, a ≠ 0
4. ∫(f1(x) + f2(x)dx = ∫f1(x)dx + ∫f2(x)dx
İntegral tablosu
Belirsiz integralde yerine koyma ve kısımlara göre integral alma.
İkame entegrasyon yöntemi yeni bir entegrasyon değişkeni (yani, bir ikame) tanıtmaktır. Bu durumda, verilen integral, tablo şeklinde olan veya ona indirgenebilen ("başarılı" bir ikame durumunda) yeni bir integrale indirgenir. İkamelerin seçilmesi için genel bir yöntem yoktur.
∫f(x)dx integralini hesaplamak istensin. φ(t)'nin sürekli türevi olan bir fonksiyon olduğu bir x =φ(t) ikamesi yapalım. Daha sonra dx \u003d φ "(t) dt ve belirsiz integrali entegre etme formülünün değişmezlik özelliğine dayanarak, ∫f (x) dx \u003d ∫ f (φ (t)) * φ '(t) dt yerine koyarak entegrasyon formülünü elde ederiz. yeni entegrasyon değişkeni t x'e geri döner.
Parçalara göre entegrasyon yöntemi
u=u(х) ve ν=v(х) sürekli türevli fonksiyonlar olsun. O zaman d(uv)=u dv+v du.
Bu eşitliği entegre ederek ∫d(uv) = ∫udv + ∫vdu elde ederiz veya
∫udv =uv - ∫vdu
Ortaya çıkan formül, parçalara göre entegrasyon formülü olarak adlandırılır. ∫udv integralinin hesaplanmasını, orijinalinden çok daha basit olabilecek ∫vdu integralinin hesaplanmasına indirgemeyi mümkün kılar.
Parçalara göre entegrasyon- İntegrandlardan biri kolayca integre edilebilirken diğeri türevlenebilir olduğunda, belirli ve belirsiz integralleri çözmek için kullanılan bir yöntem. Hem belirsiz hem de belirli integralleri bulmak için oldukça yaygın bir yöntem. Kullanmanız gerektiğinde ana işaret, doğrudan entegre edilemeyen iki işlevin bir ürününden oluşan bir işlevdir.
formül
Bu yöntemi başarılı bir şekilde kullanmak için, formülleri sökmek ve öğrenmek gerekir.
Belirsiz integralde parçalara göre entegrasyon formülü şöyledir:
$$ \int udv = uv - \int vdu $$
Belirli bir integralde parçalara göre entegrasyon formülü şöyledir:
$$ \int \limits_(a)^(b) udv = uv \bigg |_(a)^(b) - \int \limits_(a)^(b) vdu $$
Çözüm örnekleri
Testlerde genellikle öğretmenler tarafından sunulan bölümlere göre entegrasyon çözümlerinin uygulamalı örneklerini ele alalım. İntegral simgesinin altında iki işlevin ürünü olduğuna dikkat edin. Bu da bu yöntemin çözüme uygun olduğunun bir göstergesidir.
| örnek 1 |
| $ \int xe^xdx $ integralini bulun |
| Çözüm |
|
İntegrand'ın biri türev alındığında anında birliğe dönüşen ve diğerinin kolayca entegre edilen iki fonksiyondan oluştuğunu görüyoruz. İntegrali çözmek için, parçalara göre entegrasyon yöntemini kullanırız. $ u = x \rightarrow du=dx $ ve $ dv = e^x dx \rightarrow v=e^x $ olsun Bulunan değerleri ilk entegrasyon formülünde yerine koyuyoruz ve şunu elde ediyoruz: $$ \int xe^x dx = xe^x - \int e^x dx = xe^x - e^x + C $$ Sorununuzu çözemezseniz, bize gönderin. Ayrıntılı bir çözüm sunacağız. Hesaplamanın ilerleyişine kendinizi alıştırabilecek ve bilgi toplayabileceksiniz. Bu, öğretmenden zamanında bir kredi almanıza yardımcı olacaktır! |
| Cevap |
|
$$ \int xe^x dx = xe^x - e^x + C $$ |
| Örnek 4 |
| $ \int \limits_0 ^1 (x+5) 3^x dx $ integralini hesapla |
| Çözüm |
|
Daha önce çözülmüş örneklere benzeterek, hangi fonksiyonun sorunsuz bir şekilde entegre edileceğini, hangilerinin farklılaştırılacağını bulacağız. $ (x + 5) $'ı ayırt ederseniz, bu ifadenin otomatik olarak bizim için "elde" olacak birliğe dönüştürüleceğini lütfen unutmayın. Bunu bir şair olarak yapalım: $$ u=x+5 \rightarrow du=dx, dv=3^x dx \rightarrow v=\frac(3^x)(ln3) $$ Artık tüm bilinmeyen fonksiyonlar bulundu ve belirli integral için ikinci kısımlara göre entegrasyon formülüne konulabilir. $$ \int \limits_0 ^1 (x+5) 3^x dx = (x+5) \frac(3^x)(\ln 3) \bigg |_0 ^1 - \int \limits_0 ^1 \frac(3^x dx)(\ln 3) = $$ $$ = \frac(18)(\ln 3) - \frac(5)(\ln 3) - \frac(3^x)(\ln^2 3)\bigg| _0 ^1 = \frac(13)(\ln 3) - \frac(3)(\ln^2 3)+\frac(1)(\ln^2 3) = \frac(13)(\ln 3)-\frac(4)(\ln^2 3) $$ |
| Cevap |
| $$ \int\limits_0 ^1 (x+5)3^x dx = \frac(13)(\ln 3)-\frac(4)(\ln^2 3) $$ |




