Özdeğerler (sayılar) ve özvektörler Çözüm örnekleri. Doğrusal bir operatörün özvektörleri ve özdeğerleri

Köşegen tipi matrisler en basit şekilde düzenlenir. Doğrusal bir operatörün matrisinin köşegen bir forma sahip olacağı bir taban bulmanın mümkün olup olmadığı sorusu ortaya çıkar. Böyle bir temel mevcuttur.
Bir R n doğrusal uzayı ve ona etki eden bir doğrusal operatör A verilsin; bu durumda A operatörü R n'yi kendi içine alır, yani A:R n → R n .

Tanım. Sıfır olmayan bir vektöre A operatörünün özvektörü denir, eğer A operatörü ona eşdoğrusal bir vektöre çevrilirse, yani . λ sayısı, özvektöre karşılık gelen A operatörünün özdeğeri veya özdeğeri olarak adlandırılır.
Özdeğerlerin ve özvektörlerin bazı özelliklerini not ediyoruz.
1. Özvektörlerin herhangi bir doğrusal kombinasyonu aynı özdeğer λ'ya karşılık gelen A operatörünün aynı özdeğere sahip bir özvektör olduğu.
2. özvektörler ikili olarak farklı özdeğerlere sahip A operatörü λ 1 , λ 2 , …, λ m doğrusal olarak bağımsızdır.
3. Özdeğerler λ 1 =λ 2 = λ m = λ ise, o zaman özdeğer λ m'den fazla lineer bağımsız özvektöre karşılık gelmez.

Yani, eğer n lineer bağımsız özvektör varsa farklı özdeğerlere karşılık gelen λ 1 , λ 2 , …, λ n , daha sonra doğrusal olarak bağımsızdırlar, bu nedenle, R n uzayının temeli olarak alınabilirler. A operatörüyle temel vektörler üzerinde hareket ettiğimiz, özvektörleri temelinde doğrusal operatör A'nın matrisinin biçimini bulalım: Daha sonra .
Böylece, lineer operatör A'nın özvektörleri temelindeki matrisi köşegen bir forma sahiptir ve A operatörünün özdeğerleri köşegen üzerindedir.
Matrisin köşegen bir forma sahip olduğu başka bir taban var mı? Bu sorunun cevabı aşağıdaki teorem ile verilmektedir.

teorem. (i = 1..n) tabanındaki bir lineer operatör A'nın matrisi, ancak ve ancak tabandaki tüm vektörlerin A operatörünün özvektörleri olması durumunda köşegen bir forma sahiptir.

Özdeğerleri ve özvektörleri bulma kuralı

. (*)

(1)
Nerede doğrusal operatörün matrisidir.

Sistem (1), determinantı D sıfıra eşitse, sıfır olmayan bir çözüme sahiptir

Örnek 12. Doğrusal operatör A, yasaya göre R3'te hareket eder, burada x 1 , x 2 , .., x n temelde vektörün koordinatlarıdır. , , . Bu operatörün özdeğerlerini ve özvektörlerini bulun.
Çözüm. Bu operatörün matrisini oluşturuyoruz:
.
Özvektörlerin koordinatlarını belirlemek için bir sistem oluşturuyoruz:

Karakteristik denklemi oluşturuyoruz ve çözüyoruz:

.
λ 1,2 = -1, λ 3 = 3.
λ = -1'i sisteme koyarsak, şunu elde ederiz:
veya
Çünkü , o zaman iki bağımlı değişken ve bir serbest değişken vardır.
x 1 bir serbest bilinmeyen olsun, o zaman Bu sistemi herhangi bir şekilde çözeriz ve bu sistemin genel çözümünü buluruz: n - r = 3 - 2 = 1 olduğundan, temel çözüm sistemi tek çözümden oluşur.
λ = -1 özdeğerine karşılık gelen özvektörler kümesi şu biçime sahiptir: burada x 1, sıfırdan başka herhangi bir sayıdır. Örneğin, x 1 = 1 ayarlayarak bu kümeden bir vektör seçelim: .
Benzer şekilde tartışarak, özdeğer λ = 3'e karşılık gelen özvektörü buluruz: .
R3 uzayında temel, lineer olarak bağımsız üç vektörden oluşur, fakat biz sadece iki lineer olarak bağımsız özvektör elde ettik, bunlardan R3'teki baz oluşturulamaz. Sonuç olarak, doğrusal bir operatörün A matrisi köşegen bir forma indirgenemez.

Örnek 13 Verilen bir matris .
1. Vektörün olduğunu kanıtlayın A matrisinin bir özvektörüdür. Bu özvektöre karşılık gelen özdeğeri bulun.
2. A matrisinin köşegen bir forma sahip olduğu bir taban bulun.
Çözüm.
1. Eğer , o zaman bir özvektördür

.
Vektör (1, 8, -1) bir özvektördür. Özdeğer λ = -1.
Matris, özvektörlerden oluşan tabanda köşegen bir forma sahiptir. Bunlardan biri ünlü. Gerisini bulalım.
Sistemden özvektörleri arıyoruz:

Karakteristik denklem: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
λ = -3 özdeğerine karşılık gelen özvektörü bulun:

Bu sistemin matrisinin rankı ikiye ve bilinmeyenlerin sayısına eşittir, dolayısıyla bu sistemin yalnızca x 1 = x 3 = 0 sıfır çözümü vardır. x 2 burada sıfırdan başka herhangi bir şey olabilir, örneğin x 2 = 1. Böylece, (0,1,0) vektörü, λ = -3'e karşılık gelen bir özvektördür. Hadi kontrol edelim:
.
λ = 1 ise, sistemi elde ederiz
Matrisin rankı ikidir. Son denklemin üzerini çizin.
Serbest bilinmeyen x 3 olsun. Sonra x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
x 3 = 1 varsayarsak, (-3,-9,1) - özdeğer λ = 1'e karşılık gelen bir özvektörümüz var. Kontrol edin:

.
Özdeğerler gerçek ve farklı olduğundan, bunlara karşılık gelen vektörler doğrusal olarak bağımsızdır, bu nedenle R3'te temel alınabilirler. Böylece temelde , , A matrisi şu şekildedir:
.
A:R n → Rn doğrusal operatörünün her matrisi köşegen bir forma indirgenemez, çünkü bazı doğrusal operatörler için n'den daha az doğrusal olarak bağımsız özvektör olabilir. Bununla birlikte, matris simetrik ise, o zaman tam olarak m doğrusal olarak bağımsız vektörler, m çokluğunun karakteristik denkleminin köküne karşılık gelir.

Tanım. Simetrik bir matris, ana köşegene göre simetrik olan elemanların eşit olduğu, yani .
Notlar. 1. Simetrik bir matrisin tüm özdeğerleri gerçektir.
2. İkili farklı özdeğerlere karşılık gelen simetrik bir matrisin özvektörleri ortogonaldir.
Çalışılan aparatın sayısız uygulamalarından biri olarak, ikinci dereceden bir eğrinin biçimini belirleme problemini ele alıyoruz.

Bir kare matrisin özvektörü, belirli bir matrisle çarpıldığında doğrusal bir vektörle sonuçlanan bir özvektördür. Basit bir deyişle, bir matris bir özvektör ile çarpıldığında, ikincisi aynı kalır, ancak bir sayı ile çarpılır.

Tanım

Bir özvektör, bir kare matris M ile çarpıldığında kendisi haline gelen ve λ sayısı kadar artan sıfır olmayan bir V vektörüdür. Cebirsel gösterimde bu şöyle görünür:

M × V = λ × V,

burada λ, M matrisinin bir özdeğeridir.

Sayısal bir örnek ele alalım. Yazma kolaylığı için, matristeki sayılar noktalı virgülle ayrılacaktır. Diyelim ki bir matrisimiz var:

• M = 0; 4;
• 6; 10.

Bunu bir sütun vektörü ile çarpalım:

• V = -2;

Bir matrisi bir sütun vektörü ile çarptığımızda, ayrıca bir sütun vektörü elde ederiz. Katı matematik dilinde, 2 × 2'lik bir matrisi bir sütun vektörü ile çarpma formülü şöyle görünür:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

M11, M matrisinin birinci satır ve birinci sütunda yer alan elemanını, M22 ise ikinci satır ve ikinci sütunda yer alan elemanı ifade eder. Matrisimiz için bu elemanlar M11 = 0, M12 = 4, M21 = 6, M22 10'dur. Bir sütun vektörü için bu değerler V11 = -2, V21 = 1'dir. Bu formüle göre bir kare matrisin bir vektörle çarpımının aşağıdaki sonucunu elde ederiz:

• M × D = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Kolaylık sağlamak için sütun vektörünü bir satıra yazıyoruz. Böylece, kare matrisi vektörle (-2; 1) çarparak (4; -2) vektörünü elde ettik. Açıkçası, bu, λ = -2 ile çarpılan aynı vektördür. Lambda bu durumda matrisin bir özdeğerini belirtir.

Bir matrisin özvektörü, doğrusal bir vektördür, yani bir matrisle çarpıldığında uzaydaki konumunu değiştirmeyen bir nesnedir. Vektör cebirindeki eşdoğrusallık kavramı, geometrideki paralellik terimine benzer. Geometrik yorumlamada, eşdoğrusal vektörler, farklı uzunluklarda paralel yönlendirilmiş doğru parçalarıdır. Öklid zamanından beri, tek bir çizginin kendisine paralel sonsuz sayıda çizgiye sahip olduğunu biliyoruz, bu nedenle her matrisin sonsuz sayıda özvektöre sahip olduğunu varsaymak mantıklıdır.

Önceki örnekten, hem (-8; 4) hem de (16; -8) ve (32, -16)'nın özvektör olabileceği görülebilir. Tüm bunlar, λ = -2 özdeğerine karşılık gelen doğrusal vektörlerdir. Orijinal matrisi bu vektörlerle çarptığımızda, sonuç olarak orijinalden 2 kat farklı olan bir vektör elde edeceğiz. Bu nedenle, bir özvektör bulma problemlerini çözerken, sadece doğrusal olarak bağımsız vektör nesneleri bulmak gerekir. Çoğu zaman, bir n × n matris için, n'inci sayıda özvektör vardır. Hesaplayıcımız, ikinci dereceden kare matrislerin analizi için tasarlanmıştır, bu nedenle, çakıştıkları durumlar dışında neredeyse her zaman sonuç olarak iki özvektör bulunur.

Yukarıdaki örnekte, orijinal matrisin özvektörünü önceden biliyorduk ve lambda sayısını görsel olarak belirledik. Bununla birlikte, pratikte her şey tam tersi olur: başlangıçta özdeğerler ve ancak o zaman özvektörler vardır.

Çözüm algoritması

Orijinal M matrisine tekrar bakalım ve özvektörlerinin ikisini de bulmaya çalışalım. Böylece matris şöyle görünür:

• M = 0; 4;
• 6; 10.

Başlamak için, aşağıdaki matrisin determinantını hesaplamamız gereken özdeğer λ'yı belirlememiz gerekir:

• (0 - λ); 4;
• 6; (10 - λ).

Bu matris, bilinmeyen λ'nın ana köşegen üzerindeki elemanlardan çıkarılmasıyla elde edilir. Determinant, standart formülle belirlenir:

• detA = M11 × M21 - M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Vektörümüzün sıfır olmaması gerektiğinden, ortaya çıkan denklemi lineer bağımlı olarak alır ve determinant detA'mızı sıfıra eşitleriz.

(0 − λ) × (10 − λ) − 24 = 0

Parantezleri açalım ve matrisin karakteristik denklemini elde edelim:

λ 2 - 10λ - 24 = 0

Bu, diskriminant cinsinden çözülmesi gereken standart bir ikinci dereceden denklemdir.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

Diskriminantın kökü sqrt(D) = 14, dolayısıyla λ1 = -2, λ2 = 12. Şimdi her lambda değeri için bir özvektör bulmamız gerekiyor. λ = -2 için sistemin katsayılarını ifade edelim.

• M - λ × E = 2; 4;
• 6; 12.

Bu formülde, E birim matristir. Elde edilen matrise dayanarak, bir doğrusal denklem sistemi oluşturuyoruz:

2x + 4y = 6x + 12y

burada x ve y özvektörün elemanlarıdır.

Soldaki tüm X'leri ve sağdaki tüm Y'leri toplayalım. Açıkçası - 4x = 8y. İfadeyi - 4'e bölün ve x = -2y elde edin. Şimdi, bilinmeyenlerin herhangi bir değerini alarak matrisin ilk özvektörünü belirleyebiliriz (doğrusal olarak bağımlı özvektörlerin sonsuzluğunu hatırlayın). y = 1, sonra x = -2 alalım. Bu nedenle, ilk özvektör V1 = (–2; 1) gibi görünür. Makalenin başına dönün. Bir özvektör kavramını göstermek için matrisi çarptığımız şey bu vektör nesnesiydi.

Şimdi λ = 12 için özvektörü bulalım.

• M - λ × E = -12; 4
• 6; -2.

Aynı lineer denklem sistemini oluşturalım;

• -12x + 4y = 6x - 2y
• -18x = -6y
• 3x=y

Şimdi x = 1, dolayısıyla y = 3 alalım. Böylece, ikinci özvektör V2 = (1; 3) gibi görünür. Orijinal matrisi bu vektörle çarparken, sonuç her zaman aynı vektörün 12 ile çarpılması olacaktır. Bu, çözüm algoritmasını tamamlar. Artık bir matrisin özvektörünü manuel olarak nasıl tanımlayacağınızı biliyorsunuz.

• belirleyici;
• iz, yani ana köşegen üzerindeki elemanların toplamı;
• sıra, yani doğrusal olarak bağımsız satırların/sütunların maksimum sayısı.

Program yukarıdaki algoritmaya göre çalışarak çözüm sürecini en aza indirir. Programda lambda'nın "c" harfi ile gösterildiğine dikkat çekmek önemlidir. Sayısal bir örneğe bakalım.

Program örneği

Aşağıdaki matris için özvektörleri tanımlamaya çalışalım:

• M=5; 13;
• 4; 14.

Bu değerleri hesap makinesinin hücrelerine girelim ve aşağıdaki formda cevabı alalım:

• Matris sıralaması: 2;
• Matris belirleyici: 18;
• Matris izi: 19;
• Özvektör hesabı: c 2 − 19.00c + 18.00 (karakteristik denklem);
• Özvektör hesabı: 18 (ilk lambda değeri);
• Özvektör hesabı: 1 (ikinci lambda değeri);
• 1 vektörünün denklem sistemi: -13x1 + 13y1 = 4x1 - 4y1;
• Vektör 2 denklem sistemi: 4x1 + 13y1 = 4x1 + 13y1;
• Özvektör 1: (1; 1);
• Özvektör 2: (-3.25; 1).

Böylece, doğrusal olarak bağımsız iki özvektör elde ettik.

Çözüm

Doğrusal cebir ve analitik geometri, mühendislikteki herhangi bir birinci sınıf öğrencisi için standart konulardır. Çok sayıda vektör ve matris ürkütücüdür ve bu tür hantal hesaplamalarda hata yapmak kolaydır. Programımız, öğrencilerin hesaplamalarını kontrol etmelerini veya bir özvektör bulma problemini otomatik olarak çözmelerini sağlayacaktır. Kataloğumuzda başka doğrusal cebir hesaplayıcıları da var, bunları çalışmanızda veya işinizde kullanın.

www.site bulmanızı sağlar. Hesaplamayı site yapar. Birkaç saniye içinde sunucu doğru çözümü verecektir. Matris için karakteristik denklem determinantı hesaplama kuralı tarafından bulunan cebirsel bir ifade olacaktır. matrisler matrisler, ana diyagonalde ise diyagonal elemanların ve değişkenin değerlerinde farklılıklar olacaktır. Hesaplarken çevrimiçi matris için karakteristik denklem, her öğe matrisler karşılık gelen diğer öğelerle çarpılacak matrisler. modunda bul çevrimiçi sadece kare için mümkün matrisler. İşlem bul çevrimiçi matris için karakteristik denklem elemanların çarpımının cebirsel toplamını hesaplamak için azaltır matrisler determinantı bulmanın bir sonucu olarak matrisler, yalnızca belirlemek amacıyla çevrimiçi matris için karakteristik denklem. Bu işlem teoride özel bir yere sahiptir. matrisler, kökleri kullanarak özdeğerleri ve vektörleri bulmanızı sağlar. Görev bulma çevrimiçi matris için karakteristik denklem elemanları çoğaltmaktır matrisler belirli bir kurala göre bu ürünlerin müteakip toplamı ile. www.site bulur matris için karakteristik denklem modunda verilen boyut çevrimiçi. hesaplama çevrimiçi matris için karakteristik denklem belirli bir boyut için bu, determinantı hesaplama kuralı tarafından bulunan sayısal veya sembolik katsayılara sahip bir polinom bulmaktır. matrisler- karşılık gelen elemanların çarpımlarının toplamı olarak matrisler, yalnızca belirlemek amacıyla çevrimiçi matris için karakteristik denklem. Bir kare için bir değişkene göre bir polinom bulma matrisler tanım olarak matris için karakteristik denklem, teoride yaygın matrisler. Polinomun köklerinin değeri çevrimiçi matris için karakteristik denklem için özvektörleri ve özdeğerleri tanımlamak için kullanılır matrisler. Ancak belirleyici ise matrisler sıfır olacak, o zaman matris karakteristik denklemi tersinin aksine hala var olacak matrisler. hesaplamak için matris için karakteristik denklem veya aynı anda birkaç tane arayın matrisler karakteristik denklemler, sunucumuz bulurken çok zaman ve çaba harcamanız gerekiyor çevrimiçi matris için karakteristik denklem. Bu durumda, bularak cevap çevrimiçi matris için karakteristik denklem bulurken rakamlar doğru ve yeterli doğrulukta olacaktır. çevrimiçi matris için karakteristik denklem irrasyonel olacaktır. Sitede www.site elemanlarda karakter girişlerine izin verilir matrisler, yani çevrimiçi matris için karakteristik denklem hesaplanırken genel bir sembolik biçimde temsil edilebilir. karakteristik denklem matrisi çevrimiçi. bulma problemini çözerken elde edilen cevabı kontrol etmekte fayda vardır. çevrimiçi matris için karakteristik denklem siteyi kullanmak www.site. Bir polinom hesaplama işlemini gerçekleştirirken - matrisin karakteristik denklemi, bu sorunu çözmek için dikkatli ve son derece konsantre olmak gerekir. Buna karşılık, sitemiz konuyla ilgili kararınızı kontrol etmenize yardımcı olacaktır. karakteristik denklem matrisi çevrimiçi. Çözülmüş problemlerin uzun kontrolleri için zamanınız yoksa, o zaman www.site bulurken ve hesaplarken kontrol etmek için kesinlikle uygun bir araç olacaktır. çevrimiçi matris için karakteristik denklem.

HOMOJEN DOĞRUSAL DENKLEMLER SİSTEMİ

Bir homojen doğrusal denklem sistemi, bir form sistemidir.

Açıktır ki, bu durumda , Çünkü Bu belirleyicilerdeki sütunlardan birinin tüm elemanları sıfıra eşittir.

Bilinmeyenler formüllerle bulunduğundan , o zaman Δ ≠ 0 olduğu durumda, sistemin benzersiz bir sıfır çözümü vardır X = y = z= 0. Ancak birçok problemde homojen bir sistemin sıfırdan farklı çözümlerinin olup olmadığı sorusu ilgi çekicidir.

teorem. Bir doğrusal homojen denklem sisteminin sıfır olmayan bir çözüme sahip olması için Δ ≠ 0 olması gerekli ve yeterlidir.

Dolayısıyla, determinant Δ ≠ 0 ise, o zaman sistemin tek bir çözümü vardır. Δ ≠ 0 ise, lineer homojen denklemler sisteminin sonsuz sayıda çözümü vardır.

Örnekler.

Özvektörler ve Matris Özdeğerleri

Bir kare matris verilsin , X yüksekliği matrisin düzeniyle çakışan bir matris sütunudur A. .

Birçok problemde, denklemi dikkate almak gerekir. X

burada λ bir sayıdır. Herhangi bir λ için bu denklemin sıfır çözümü olduğu açıktır.

Bu denklemin sıfır olmayan çözümü olan λ sayısına denir. özdeğer matrisler A, A X böyle bir λ için denir kendi vektörü matrisler A.

Matrisin özvektörünü bulalım A. Çünkü E∙X=X, o zaman matris denklemi şu şekilde yeniden yazılabilir: veya . Genişletilmiş formda, bu denklem bir doğrusal denklem sistemi olarak yeniden yazılabilir. Gerçekten .

Ve bu nedenle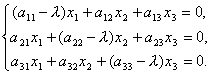

Böylece, koordinatları belirlemek için bir homojen doğrusal denklem sistemimiz var. x 1, x2, x 3 vektör X. Sistemin sıfır olmayan çözümlere sahip olması için sistemin determinantının sıfıra eşit olması gerekli ve yeterlidir.

Bu, λ'ya göre 3. dereceden bir denklemdir. denir karakteristik denklem matrisler A ve λ özdeğerlerini belirlemeye yarar.

Her özdeğer λ bir özvektöre karşılık gelir X, koordinatları sistemden ilgili λ değerinde belirlenir.

Örnekler.

VEKTÖR CEBİR. VEKTÖR KONSEPTİ

Fiziğin çeşitli dallarını incelerken, örneğin uzunluk, alan, kütle, sıcaklık vb. sayısal değerleri ayarlanarak tamamen belirlenen nicelikler vardır. Bu tür değerlere skaler denir. Bununla birlikte, bunlara ek olarak, sayısal değere ek olarak, örneğin, vücuda etki eden kuvvet, uzayda hareket ederken vücudun hızı ve ivmesi, uzayda belirli bir noktadaki manyetik alan kuvveti gibi uzaydaki yönlerinin de bilinmesi gereken nicelikler de vardır. Bu niceliklere vektör nicelikleri denir.

Kesin bir tanım getirelim.

yönlü segment Uçlarına göre hangisinin birinci hangisinin ikinci olduğu bilinen bir doğru parçası diyelim.

Vektör belirli bir uzunluğa sahip, yani yönlendirilmiş bir segment denir. Bu, onu sınırlayan noktalardan birinin başlangıç ​​​​ve ikincisinin bitiş olarak alındığı belirli bir uzunlukta bir segmenttir. Eğer A vektörün başlangıcıdır, B sonu ise, vektör sembolle gösterilir, ayrıca vektör genellikle tek bir harfle gösterilir. Şekilde, vektör bir parça ile ve yönü bir okla gösterilmiştir.

modül veya uzunluk vektör, onu tanımlayan yönlendirilmiş segmentin uzunluğu olarak adlandırılır. || ile gösterilir veya ||.

Başlangıcı ve sonu çakışan sözde sıfır vektörü de vektör olarak anılacaktır. İşaretlendi. Sıfır vektörünün belirli bir yönü yoktur ve modülü sıfır ||=0'a eşittir.

Vektörler ve denir doğrusal aynı hat üzerinde veya paralel hatlar üzerinde bulunuyorlarsa. Bu durumda, eğer ve vektörleri eşit yönlü ise, tersini yazacağız.

Aynı düzleme paralel doğrular üzerinde bulunan vektörlere ne ad verilir? aynı düzlemde.

İki vektör ve denir eşit eşdoğrusal iseler, aynı yöne sahiptirler ve uzunlukları eşittir. Bu durumda yazın.

Vektörlerin eşitliği tanımından, bir vektörün orijini uzayda herhangi bir noktaya yerleştirilerek kendisine paralel hareket ettirilebileceği sonucu çıkar.

Örneğin.

VEKTÖRLER ÜZERİNDE DOĞRUSAL İŞLEMLER

1. Bir vektörü bir sayı ile çarpmak.

   Bir vektörün λ sayısı ile çarpımı, aşağıdaki gibi yeni bir vektördür:

   Bir vektörün ve bir sayının çarpımı λ ile gösterilir.

   

   Örneğin, vektörle aynı yönü gösteren ve vektörün yarısı kadar uzunluğa sahip bir vektördür.

   Girilen işlem aşağıdakilere sahiptir özellikler:

2. Vektörlerin eklenmesi.

   Izin verin ve iki keyfi vektör olsun. Keyfi bir nokta alın Ö ve bir vektör oluşturun. Bundan sonra noktadan A vektörü bir kenara bırakın. Birinci vektörün başlangıcı ile ikinci vektörün sonunu birleştiren vektöre ne ad verilir? toplam bu vektörlerin ve gösterilir .

   

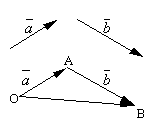
   Vektör toplamanın formüle edilmiş tanımına denir. paralelkenar kuralı, çünkü aynı vektör toplamı aşağıdaki gibi elde edilebilir. Noktadan bir kenara koyun Ö vektörler ve . Bu vektörler üzerinde bir paralelkenar oluşturun OABC. Vektörler olduğundan, tepe noktasından çizilen paralelkenarın köşegeni olan vektör Ö, açıkça vektörlerin toplamı olacaktır.

   

   Aşağıdakileri kontrol etmek kolaydır vektör toplama özellikleri.

3. Vektörlerin farkı.

   Belirli bir vektöre eşdoğrusal olan, uzunluğu eşit ve zıt yönlü bir vektöre ne ad verilir? zıt bir vektör için vektör ve ile gösterilir. Zıt vektör, λ = –1 sayısı ile vektör çarpımının sonucu olarak düşünülebilir: .

A matrisi ile, AX = lX olacak şekilde bir l sayısı varsa.

Bu durumda, l sayısı denir özdeğer X vektörüne karşılık gelen operatör (matris A).

Başka bir deyişle, bir özvektör, doğrusal bir operatörün etkisi altında eşdoğrusal bir vektöre dönüşen bir vektördür, yani. sadece bir sayı ile çarpın. Tersine, uygunsuz vektörlerin dönüştürülmesi daha zordur.

Özvektörün tanımını bir denklem sistemi olarak yazıyoruz:

Tüm terimleri sol tarafa taşıyalım:

Son sistem matris formunda aşağıdaki gibi yazılabilir:

(A - lE)X \u003d O

Ortaya çıkan sistemin her zaman sıfır çözümü vardır X = O. Tüm serbest terimlerin sıfıra eşit olduğu bu tür sistemlere denir. homojen. Böyle bir sistemin matrisi kare ise ve determinantı sıfıra eşit değilse, o zaman Cramer'in formüllerine göre her zaman benzersiz bir çözüm - sıfır elde edeceğiz. Sistemin sıfır olmayan çözümlere sahip olduğu ancak ve ancak bu matrisin determinantının sıfıra eşit olması durumunda kanıtlanabilir, yani.

|A - lE| = = 0

Bilinmeyen l ile bu denklem denir karakteristik denklem (karakteristik polinom) A matrisi (doğrusal operatör).

Doğrusal bir operatörün karakteristik polinomunun taban seçimine bağlı olmadığı kanıtlanabilir.

Örneğin A = matrisinin verdiği lineer operatörün özdeğerlerini ve özvektörlerini bulalım.

Bunu yapmak için |А - lЕ| karakteristik denklemini oluşturuyoruz. = \u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; özdeğerler l 1 = (2 - 12)/2 = -5; 2 \u003d (2 + 12) / 2 \u003d 7.

Özvektörleri bulmak için iki denklem sistemini çözeriz

(A + 5E) X = Ö

(A - 7E) X = O

Bunlardan ilki için, genişletilmiş matris şu şekli alacaktır:

,

bu nedenle x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, yani X (1) \u003d (- (2/3) s; s).

İkincisi için, genişletilmiş matris şu şekli alacaktır:

,

bu nedenle x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, yani X (2) \u003d ((2/3) s 1; s 1).

Böylece, bu lineer operatörün özvektörleri özdeğeri (-5) olan (-(2/3)c; c) şeklindeki tüm vektörler ve özdeğeri 7 olan ((2/3)c 1 ; c 1) şeklindeki tüm vektörlerdir.

Özvektörlerinden oluşan temelde A operatörünün matrisinin köşegen olduğu ve şu şekilde olduğu kanıtlanabilir:

,

burada l ben bu matrisin özdeğerleridir.

Tersi de doğrudur: eğer A matrisi bazı bazlarda köşegen ise, bu bazın tüm vektörleri bu matrisin özvektörleri olacaktır.

Ayrıca, bir lineer operatörün n ikili farklı özdeğere sahip olması durumunda, karşılık gelen özvektörlerin lineer olarak bağımsız olduğu ve bu operatörün ilgili temelde matrisinin köşegen bir forma sahip olduğu da kanıtlanabilir.

Bunu bir önceki örnekle açıklayalım. Keyfi sıfır olmayan değerler alalım c ve c 1 , ancak X (1) ve X (2) vektörleri doğrusal olarak bağımsız olacak şekilde, yani. bir temel oluşturacaktı. Örneğin, c \u003d c 1 \u003d 3, ardından X (1) \u003d (-2; 3), X (2) \u003d (2; 3) olsun.

Bu vektörlerin doğrusal bağımsızlığını doğrulayalım:

12 ≠ 0. Bu yeni temelde, A matrisi A * = şeklini alacaktır.

Bunu doğrulamak için A * = C -1 AC formülünü kullanıyoruz. Önce C -1'i bulalım.

C-1 = ;

İkinci dereceden formlar

ikinci dereceden biçim n değişkenden f (x 1, x 2, x n), her terimi değişkenlerden birinin karesi veya belirli bir katsayı ile alınan iki farklı değişkenin çarpımı olan toplam olarak adlandırılır: f (x 1, x 2, x n) = (bir ij = bir ji).

Bu katsayılardan oluşan A matrisine denir. matris ikinci dereceden biçim. Her zaman simetrik matris (yani, ana köşegene göre simetrik bir matris, a ij = a ji).

Matris notasyonunda, ikinci dereceden form f(X) = X T AX şeklindedir; burada

Aslında

Örneğin ikinci dereceden formu matris formunda yazalım.

Bunu yapmak için, ikinci dereceden bir formun matrisini buluruz. Köşegen elemanları, değişkenlerin karelerindeki katsayılara eşittir ve geri kalan elemanlar, ikinci dereceden formun karşılık gelen katsayılarının yarısına eşittir. Bu yüzden

X değişkenlerinin matris sütunu, Y matris sütununun dejenere olmayan doğrusal dönüşümüyle elde edilsin, yani X = CY, burada C, n mertebesinde dejenere olmayan bir matristir. O halde ikinci dereceden f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y formu.

Böylece, dejenere olmayan bir doğrusal dönüşüm C altında, ikinci dereceden formun matrisi şu formu alır: A * = C T AC.

Örneğin f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 ikinci dereceden formundan doğrusal dönüşümle elde edilen ikinci dereceden f(y 1, y 2) formunu bulalım.

İkinci dereceden forma denir kanonik(Sahiptir kanonik görünüm) i ≠ j için tüm katsayıları a ij = 0 ise, yani
f(x 1, x 2, x n) = bir 11 x 1 2 + bir 22 x 2 2 + bir nn x n 2 =.

Matrisi köşegendir.

teorem(kanıt burada verilmemiştir). Herhangi bir ikinci dereceden form, dejenere olmayan bir doğrusal dönüşüm kullanılarak kanonik bir forma indirgenebilir.

Örneğin, ikinci dereceden formu kanonik forma indirgeyelim.
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

Bunu yapmak için önce x 1 değişkeni için tam kareyi seçin:

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2) 2 - 5x 2 2 - x 2 x 3.

Şimdi x 2 değişkeni için tam kareyi seçiyoruz:

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2) + (5/100) x 3 2 \u003d
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

Daha sonra dejenere olmayan bir doğrusal dönüşüm y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 ve y 3 \u003d x 3, bu ikinci dereceden formu f (y 1, y 2, y 3) \u003d 2y 1 2 - 5y 2 2 + (1/20) y kanonik formuna indirger 3 2.

İkinci dereceden bir formun kanonik formunun belirsiz bir şekilde tanımlandığına dikkat edin (aynı ikinci dereceden form, farklı şekillerde kanonik forma indirgenebilir). Bununla birlikte, çeşitli yöntemlerle elde edilen kanonik formların bir takım ortak özellikleri vardır. Özellikle, ikinci dereceden bir formun pozitif (negatif) katsayılarına sahip terimlerin sayısı, formun bu forma nasıl indirgendiğine bağlı değildir (örneğin, ele alınan örnekte her zaman iki negatif ve bir pozitif katsayı olacaktır). Bu özelliğe ikinci dereceden formların eylemsizlik yasası denir.

Aynı ikinci dereceden formu kanonik forma farklı bir şekilde indirgeyerek bunu doğrulayalım. Dönüşüme x 2 değişkeni ile başlayalım:

f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d -3 (x 2 2 +
+ 2* x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \u003d f (y 1, y 2, y 3) \u003d -3y 1 2 -
+ 3y 2 2 + 2y 3 2, burada y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6) x 3 ve y 3 \u003d x 1. Burada, y1'de negatif bir katsayı -3 ve y2 ve y3'te iki pozitif katsayı 3 ve 2 (ve başka bir yöntem kullanarak, y2'de negatif bir katsayı (-5) ve iki pozitif katsayı elde ettik: y1'de 2 ve y3'te 1/20).

Ayrıca, ikinci dereceden bir formdaki bir matrisin sırasının, adı verilen not edilmelidir. ikinci dereceden formun sıralaması, kanonik formun sıfır olmayan katsayılarının sayısına eşittir ve doğrusal dönüşümler altında değişmez.

İkinci dereceden forma f(X) denir olumlu (olumsuz) kesin, aynı anda sıfıra eşit olmayan değişkenlerin tüm değerleri için pozitif ise, yani. f(X) > 0 (negatif, yani
f(X)< 0).

Örneğin, f 1 (X) \u003d x 1 2 + x 2 2 ikinci dereceden form pozitif tanımlıdır, çünkü karelerin toplamıdır ve f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 ikinci dereceden form negatif tanımlıdır, çünkü f 2 (X) \u003d - (x 1 - x 2) 2 olarak temsil edilebileceğini temsil eder.

Çoğu pratik durumda, ikinci dereceden bir formun işaret kesinliğini oluşturmak biraz daha zordur, bu nedenle bunun için aşağıdaki teoremlerden biri kullanılır (bunları kanıt olmadan formüle ederiz).

teorem. İkinci dereceden bir form, ancak ve ancak matrisinin tüm özdeğerleri pozitif (negatif) ise pozitif (negatif) kesindir.

teorem(Sylvester'ın kriteri). İkinci dereceden bir form, ancak ve ancak bu formun matrisinin tüm asal minörleri pozitifse pozitif tanımlıdır.

majör (köşe) minör n'inci mertebeden A matrisinin k'inci mertebesine, A matrisinin () ilk k satırından ve sütunundan oluşan matrisin determinantı denir.

Negatif-belirli ikinci dereceden formlar için, asıl minörlerin işaretlerinin dönüşümlü olduğunu ve birinci dereceden minörün negatif olması gerektiğini unutmayın.

Örneğin, işaret kesinliği için ikinci dereceden f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 formunu inceliyoruz.

= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D = 25 - 8 = 17;
. Bu nedenle, ikinci dereceden biçim pozitif tanımlıdır.

Yöntem 2. Matrisin birinci mertebesinin ana minörü A D 1 = a 11 = 2 > 0. İkinci mertebenin ana minörü D 2 = = 6 - 4 = 2 > 0. Dolayısıyla Sylvester kriterine göre ikinci dereceden form pozitif tanımlıdır.

İşaret kesinliği için başka bir ikinci dereceden formu inceliyoruz, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Yöntem 1. A = ikinci dereceden bir matris oluşturalım. Karakteristik denklem şu şekle sahip olacaktır: = (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l2) - 4 = l2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Bu nedenle, ikinci dereceden biçim negatif tanımlıdır.

Yöntem 2. A D 1 = a 11 = matrisinin birinci mertebesinin ana minörü
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Bu nedenle, Sylvester kriterine göre, ikinci dereceden biçim negatif tanımlıdır (ana minörlerin işaretleri eksiden başlayarak değişir).

Ve başka bir örnek olarak, işaret kesinliği için ikinci dereceden f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 formunu inceliyoruz.

Yöntem 1. A = ikinci dereceden bir matris oluşturalım. Karakteristik denklem şu şekle sahip olacaktır: = (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l2) - 4 = l2 + l - 10 = 0; D = 1 + 40 = 41;
.

Bu sayılardan biri negatif, diğeri pozitiftir. Özdeğerlerin işaretleri farklıdır. Bu nedenle, ikinci dereceden bir form, negatif veya pozitif tanımlı olamaz, yani bu ikinci dereceden biçim işaret tanımlı değildir (herhangi bir işaretin değerini alabilir).

Yöntem 2. Matrisin birinci mertebesinin ana minörü A D 1 = a 11 = 2 > 0. İkinci mertebenin ana minörü D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).