Собствени стойности (числа) и собствени вектори.
Примери за решения

Бъди себе си

От двете уравнения следва, че .

Да го поставим тогава: .

Като резултат: – втори собствен вектор.

Нека повторим важните моменти от решението:

– получената система със сигурност има общо решение (уравненията са линейно зависими);

– избираме „y“ по такъв начин, че да е цяло число и първата координата „x“ да е цяло число, положителна и възможно най-малка.

– проверяваме дали конкретното решение удовлетворява всяко уравнение на системата.

Отговор .

Имаше достатъчно междинни „контролни точки“, така че проверката на равенството по принцип не е необходима.

В различни източници на информация координатите на собствените вектори често се записват не в колони, а в редове, например: (и, честно казано, аз самият съм свикнал да ги записвам на редове). Този вариант е приемлив, но в светлината на темата линейни трансформациитехнически по-удобен за използване колонни вектори.

Може би решението ви се стори много дълго, но това е само защото коментирах първия пример много подробно.

Пример 2

Матрици

Да тренираме сами! Примерен пример за финална задача в края на урока.

Понякога трябва да изпълните допълнителна задача, а именно:

напишете разлагането на каноничната матрица

Какво е?

Ако собствените вектори на матрицата образуват база, то може да се представи като:

Където е матрица, съставена от координати на собствени вектори, – диагоналматрица със съответните собствени стойности.

Това матрично разлагане се нарича канониченили диагонал.

Нека да разгледаме матрицата на първия пример. Неговите собствени вектори линейно независими(неколинеарни) и образуват основа. Нека създадем матрица на техните координати:

На главен диагоналматрици в съответния редсобствените стойности са разположени, а останалите елементи са равни на нула:
– Още веднъж подчертавам важността на реда: „две” съответства на 1-ви вектор и следователно се намира в 1-ва колона, „три” – на 2-ри вектор.

Използвайки обичайния алгоритъм за намиране обратна матрицаили Метод на Гаус-Джорданнамираме . Не, това не е печатна грешка! - пред вас е рядко събитие, като слънчево затъмнение, когато обратната страна съвпадна с оригиналната матрица.

Остава да напишем каноничното разлагане на матрицата:

Системата може да бъде решена чрез елементарни трансформации и в следващите примери ще прибегнем до този метод. Но тук „училищният“ метод работи много по-бързо. От 3-то уравнение изразяваме: – заместваме във второто уравнение:

Тъй като първата координата е нула, получаваме система, от всяко уравнение на която следва, че .

И отново обърнете внимание на задължителното наличие на линейна зависимост. Ако се получи само тривиално решение , тогава или собствената стойност е намерена неправилно, или системата е компилирана/решена с грешка.

Компактните координати дават стойността

Собствен вектор:

И още веднъж проверяваме дали решението е намерено удовлетворява всяко уравнение на системата. В следващите параграфи и в следващите задачи препоръчвам да вземете това желание като задължително правило.

2) За собствената стойност, използвайки същия принцип, получаваме следната система:

От второто уравнение на системата изразяваме: – заместваме в третото уравнение:

Тъй като координатата "дзета" е равна на нула, получаваме система от всяко уравнение, от която следва линейна зависимост.

Позволявам

Проверка дали решението удовлетворява всяко уравнение на системата.

Така собственият вектор е: .

3) И накрая, системата съответства на собствената стойност:

Второто уравнение изглежда най-просто, така че нека го изразим и заместим в 1-во и 3-то уравнения:

Всичко е наред - появи се линейна връзка, която заместваме в израза:

В резултат на това „x“ и „y“ бяха изразени чрез „z“: . На практика не е необходимо да се постигат точно такива отношения, в някои случаи е по-удобно да се изразяват и двете чрез или и чрез . Или дори „влак“ - например „X“ през „I“ и „I“ през „Z“

Да го поставим тогава:

Проверяваме дали решението е намерено удовлетворява всяко уравнение на системата и записва третия собствен вектор

Отговор: собствени вектори:

Геометрично тези вектори определят три различни пространствени посоки ("До там и обратно"), според която линейна трансформациятрансформира ненулеви вектори (собствени вектори) в колинеарни вектори.

Ако условието изисква намиране на каноничното разлагане, тогава това е възможно тук, защото различни собствени стойности съответстват на различни линейно независими собствени вектори. Изработване на матрица от техните координати, диагонална матрица от релевантнисобствени стойности и намерете обратна матрица .

Ако по условие трябва да пишете линейна трансформационна матрица в основата на собствените вектори, тогава даваме отговора във формата . Разлика има и то значителна!Тъй като тази матрица е "de" матрицата.

Задача с по-прости изчисления, която можете да решите сами:

Пример 5

Намерете собствени вектори на линейна трансформация, дадена от матрица

Когато намирате свои собствени числа, опитайте се да не стигнете до полином от 3-та степен. В допълнение, вашите системни решения може да се различават от моите решения - тук няма сигурност; и векторите, които намирате, могат да се различават от примерните вектори до пропорционалността на съответните им координати. Например и. По-естетично е да представите отговора във формуляра, но е добре, ако се спрете на втория вариант. Има обаче разумни ограничения за всичко; версията вече не изглежда много добре.

Приблизителна окончателна извадка на заданието в края на урока.

Как да решим проблема в случай на множество собствени стойности?

Общият алгоритъм остава същият, но има свои собствени характеристики и е препоръчително да запазите някои части от решението в по-строг академичен стил:

Пример 6

Намерете собствени стойности и собствени вектори

Решение

Разбира се, нека изписваме страхотната първа колона с главни букви:

И след факторизиране на квадратния трином:

В резултат на това се получават собствени стойности, две от които са кратни.

Нека намерим собствените вектори:

1) Нека се справим със самотен войник по „опростена“ схема:

От последните две уравнения ясно се вижда равенството, което очевидно трябва да бъде заменено в 1-вото уравнение на системата:

Няма да намерите по-добра комбинация:
Собствен вектор:

2-3) Сега премахваме няколко часови. В този случай може да се окаже или две или еднасобствен вектор. Независимо от множествеността на корените, заместваме стойността в детерминантата което ни води до следващия хомогенна система от линейни уравнения:

Собствените вектори са точно вектори
фундаментална система от решения

Всъщност през целия урок ние не правихме нищо, освен да намерим векторите на фундаменталната система. Просто засега този термин не беше особено необходим. Между другото, тези умни студенти, които са пропуснали темата в камуфлажни костюми хомогенни уравнения, ще бъде принуден да го изпуши сега.

Единственото действие беше премахването на допълнителните линии. Резултатът е матрица едно по три с формална „стъпка“ в средата.
– основна променлива, – свободни променливи. Следователно има две свободни променливи има и два вектора на фундаменталната система.

Нека изразим основната променлива чрез свободни променливи: . Нулевият множител пред „X“ му позволява да приема абсолютно всякакви стойности (което е ясно видимо от системата от уравнения).

В контекста на този проблем е по-удобно да напишете общото решение не в ред, а в колона:

Двойката съответства на собствен вектор:
Двойката съответства на собствен вектор:

Забележка : опитните читатели могат да избират тези вектори устно - просто като анализират системата , но тук са необходими известни знания: има три променливи, ранг на системната матрица- едно, което означава фундаментална система за вземане на решениясе състои от 3 – 1 = 2 вектора. Намерените вектори обаче са ясно видими и без това знание, чисто на интуитивно ниво. В този случай третият вектор ще бъде написан още по-красиво: . Предупреждавам ви обаче, че в друг пример обикновеният избор може да не е възможен, поради което клаузата е предназначена за хора с опит. В допълнение, защо не вземете, да речем, като трети вектор? В края на краищата неговите координати също удовлетворяват всяко уравнение на системата и векторите линейно независими. Тази опция по принцип е подходяща, но „крива“, тъй като „другият“ вектор е линейна комбинация от вектори на основната система.

Отговор: собствени стойности: , собствени вектори:

Подобен пример за независимо решение:

Пример 7

Намерете собствени стойности и собствени вектори

Приблизителна проба на окончателния дизайн в края на урока.

Трябва да се отбележи, че както в 6-ия, така и в 7-ия пример се получава тройка от линейно независими собствени вектори и следователно оригиналната матрица е представима в каноничното разлагане. Но такива малини не се случват във всички случаи:

Пример 8

Решение: Нека създадем и решим характеристичното уравнение:

Нека разширим детерминантата в първата колона:

Извършваме допълнителни опростявания според разглеждания метод, като избягваме полинома от трета степен:

– собствени стойности.

Нека намерим собствените вектори:

1) Няма трудности с корена:

Не се изненадвайте, в допълнение към комплекта има и променливи в употреба - тук няма разлика.

От 3-то уравнение го изразяваме и го заместваме в 1-во и 2-ро уравнения:

От двете уравнения следва:

Нека тогава:

2-3) За множество стойности получаваме системата .

Нека напишем матрицата на системата и, използвайки елементарни трансформации, я привеждаме в поетапна форма:

Диагоналните матрици имат най-проста структура. Възниква въпросът дали е възможно да се намери базис, в който матрицата на линейния оператор да има диагонална форма. Такава база съществува.
Нека ни е дадено линейно пространство R n и действащ в него линеен оператор A; в този случай оператор A приема R n в себе си, тоест A:R n → R n .

Определение. Ненулев вектор се нарича собствен вектор на оператора A, ако операторът A се транслира в колинеарен вектор, т.е. Числото λ се нарича собствена стойност или собствена стойност на оператора A, съответстващ на собствения вектор.
Нека да отбележим някои свойства на собствените стойности и собствените вектори.
1. Всяка линейна комбинация от собствени вектори оператор A, съответстващ на същата собствена стойност λ, е собствен вектор със същата собствена стойност.
2. Собствени вектори оператор A с по двойки различни собствени стойности λ 1 , λ 2 , …, λ m са линейно независими.
3. Ако собствените стойности λ 1 =λ 2 = λ m = λ, тогава собствената стойност λ съответства на не повече от m линейно независими собствени вектора.

Така че, ако има n линейно независими собствени вектора , съответстващи на различни собствени стойности λ 1, λ 2, ..., λ n, тогава те са линейно независими, следователно могат да бъдат взети като основа на пространството R n. Нека намерим формата на матрицата на линейния оператор A в базиса на неговите собствени вектори, за които ще действаме с оператора A върху базисните вектори: Тогава .
По този начин матрицата на линейния оператор A в основата на неговите собствени вектори има диагонална форма, а собствените стойности на оператора A са по диагонала.
Има ли друга основа, в която матрицата има диагонална форма? Отговорът на този въпрос се дава от следната теорема.

Теорема. Матрицата на линеен оператор A в базиса (i = 1..n) има диагонална форма тогава и само ако всички вектори на базиса са собствени вектори на оператора A.

Правило за намиране на собствени стойности и собствени вектори

. (*)

(1)
Където - линейна операторна матрица.

Система (1) има ненулево решение, ако нейната детерминанта D е равна на нула

Пример 12. Линейният оператор A действа в R 3 по закона, където x 1, x 2, .., x n са координатите на вектора в основата , , . Намерете собствените стойности и собствените вектори на този оператор.
Решение. Изграждаме матрицата на този оператор:
.
Създаваме система за определяне на координатите на собствените вектори:

Съставяме характеристично уравнение и го решаваме:

.
λ 1,2 = -1, λ 3 = 3.
Замествайки λ = -1 в системата, имаме:
или
защото , тогава има две зависими променливи и една свободна променлива.
Тогава нека x 1 е свободно неизвестно Решаваме тази система по произволен начин и намираме общото решение на тази система: Фундаменталната система от решения се състои от едно решение, тъй като n - r = 3 - 2 = 1.
Множеството от собствени вектори, съответстващи на собствената стойност λ = -1, има формата: , където x 1 е всяко число, различно от нула. Нека изберем един вектор от този набор, например, като поставим x 1 = 1: .
Разсъждавайки по подобен начин, намираме собствения вектор, съответстващ на собствената стойност λ = 3: .
В пространството R 3 базисът се състои от три линейно независими вектора, но получихме само два линейно независими собствени вектора, от които не може да бъде съставен базисът в R 3. Следователно не можем да редуцираме матрицата A на линеен оператор до диагонална форма.

Пример 13. Дадена е матрица .
1. Докажете, че векторът е собствен вектор на матрица A. Намерете собствената стойност, съответстваща на този собствен вектор.
2. Намерете базис, в който матрицата A има диагонална форма.
Решение.
1. Ако , тогава е собствен вектор

.
Вектор (1, 8, -1) е собствен вектор. Собствена стойност λ = -1.
Матрицата има диагонална форма в основа, състояща се от собствени вектори. Един от тях е известен. Нека намерим останалите.
Търсим собствени вектори от системата:

Характеристично уравнение: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Нека намерим собствения вектор, съответстващ на собствената стойност λ = -3:

Рангът на матрицата на тази система е две и е равен на броя на неизвестните, така че тази система има само нулево решение x 1 = x 3 = 0. x 2 тук може да бъде нещо различно от нула, например x 2 = 1. Така векторът (0 ,1,0) е собствен вектор, съответстващ на λ = -3. Да проверим:
.
Ако λ = 1, тогава получаваме системата
Рангът на матрицата е две. Задраскваме последното уравнение.
Нека x 3 е свободно неизвестно. Тогава x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Ако приемем, че x 3 = 1, имаме (-3,-9,1) - собствен вектор, съответстващ на собствената стойност λ = 1. Проверете:

.
Тъй като собствените стойности са реални и различни, векторите, съответстващи на тях, са линейно независими, така че те могат да бъдат взети като основа в R 3 . По този начин в основата , , матрица А има формата:
.
Не всяка матрица на линеен оператор A:R n → R n може да бъде редуцирана до диагонална форма, тъй като за някои линейни оператори може да има по-малко от n линейни независими собствени вектора. Въпреки това, ако матрицата е симетрична, тогава коренът на характеристичното уравнение на множествеността m съответства на точно m линейно независими вектора.

Определение. Симетричната матрица е квадратна матрица, в която елементите, симетрични спрямо главния диагонал, са равни, т.е. в която .
Бележки. 1. Всички собствени стойности на симетрична матрица са реални.
2. Собствените вектори на симетрична матрица, съответстваща на различни по двойки собствени стойности, са ортогонални.
Като едно от многото приложения на изследваната апаратура, ние разглеждаме проблема за определяне на вида на крива от втори ред.

Определение 9.3.вектор х Наречен собствен векторматрици А, ако има такъв номер λ, че е в сила равенството: А х= λ х, тоест резултатът от прилагането на х линейна трансформация, зададена от матрицата А, е умножението на този вектор по числото λ . Самото число λ Наречен собствена стойностматрици А.

Заместване във формули (9.3) x` j = λx j,получаваме система от уравнения за определяне на координатите на собствения вектор:

. (9.5)

Тази линейна хомогенна система ще има нетривиално решение само ако нейният основен детерминант е 0 (правило на Крамър). Като напишете това условие във формата:

получаваме уравнение за определяне на собствените стойности λ , Наречен характеристично уравнение. Накратко може да се представи по следния начин:

| A - λE | = 0, (9.6)

тъй като лявата му страна съдържа детерминантата на матрицата A-λE. Относителен полином λ | A - λE| Наречен характерен полиномматрици А.

Свойства на характеристичния полином:

1) Характеристичният полином на линейна трансформация не зависи от избора на базис. Доказателство. (виж (9.4)), но следователно, . По този начин не зависи от избора на основа. Това означава, че | A-λE| не се променя при преминаване към нова основа.

2) Ако матрицата Алинейната трансформация е симетричен(тези. и ij =a ji), тогава всички корени на характеристичното уравнение (9.6) са реални числа.

Свойства на собствените стойности и собствените вектори:

1) Ако изберете базис от собствените вектори x 1, x 2, x 3 , съответстващи на собствените стойности λ 1, λ 2, λ 3матрици А, тогава в тази база линейната трансформация A има матрица с диагонална форма:

(9.7) Доказателството за това свойство следва от дефиницията на собствените вектори.

2) Ако собствените стойности на трансформацията Аса различни, тогава съответните им собствени вектори са линейно независими.

3) Ако характеристичният полином на матрицата Аима три различни корена, тогава в някакъв базис матрицата Аима диагонален вид.

Нека намерим собствените стойности и собствените вектори на матрицата. Нека създадем характеристично уравнение: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Нека намерим координатите на собствените вектори, съответстващи на всяка намерена стойност λ. От (9.5) следва, че ако х (1) ={x 1, x 2, x 3) – съответен собствен вектор λ 1 =-2, тогава

- кооперативна, но несигурна система. Неговото решение може да бъде записано във формата х (1) ={а,0,-а), където a е произволно число. По-специално, ако изискваме | х (1) |=1, х (1) =

Заместване в системата (9.5) λ 2 =3, получаваме система за определяне на координатите на втория собствен вектор - х (2) ={y 1, y 2, y 3}:

, където х (2) ={b,-b,b) или при условие | х (2) |=1, х (2) =

За λ 3 = 6 намерете собствения вектор х (3) ={z 1, z 2, z 3}:

, х (3) ={° С,2c,c) или в нормализирана версия

x (3) = Може да се забележи, че х (1) х (2) = аб–аб= 0, х (1) х (3) = ac-ac= 0, х (2) х (3) = пр.н.е- 2пр.н.е= 0. Следователно собствените вектори на тази матрица са по двойки ортогонални.

Лекция 10.

Квадратни форми и връзката им със симетрични матрици. Свойства на собствените вектори и собствените стойности на симетрична матрица. Намаляване на квадратна форма до канонична форма.

Определение 10.1.Квадратна формареални променливи x 1, x 2,…, x nсе нарича полином от втора степен в тези променливи, който не съдържа свободен член и членове от първа степен.

Примери за квадратни форми:

(н = 2),

(н = 3). (10.1)

Нека си припомним дефиницията на симетрична матрица, дадена в миналата лекция:

Определение 10.2.Квадратната матрица се нарича симетричен, ако , т.е. ако елементите на матрицата, които са симетрични спрямо главния диагонал, са равни.

Свойства на собствените стойности и собствените вектори на симетрична матрица:

1) Всички собствени стойности на симетрична матрица са реални.

Доказателство (за н = 2).

Нека матрицата Аима формата: . Нека създадем характеристично уравнение:

(10.2) Нека намерим дискриминанта:

Следователно уравнението има само реални корени.

2) Собствените вектори на симетрична матрица са ортогонални.

Доказателство (за н= 2).

Координатите на собствените вектори и трябва да удовлетворяват уравненията.

Собствен вектор на квадратна матрица е този, който, когато се умножи по дадена матрица, води до колинеарен вектор. С прости думи, когато една матрица се умножи по собствен вектор, последният остава същият, но умножен по определено число.

Определение

Собственият вектор е ненулев вектор V, който, когато се умножи по квадратна матрица M, сам се увеличава с някакво число λ. В алгебрична нотация изглежда така:

M × V = λ × V,

където λ е собствената стойност на матрицата M.

Нека да разгледаме числен пример. За по-лесно записване числата в матрицата ще бъдат разделени с точка и запетая. Нека имаме матрица:

• М = 0; 4;
• 6; 10.

Нека го умножим по колонен вектор:

• V = -2;

Когато умножим една матрица по вектор колона, ние също получаваме вектор колона. На строг математически език формулата за умножаване на матрица 2 × 2 по вектор на колона ще изглежда така:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 означава елемента на матрицата M, разположен в първия ред и първата колона, а M22 означава елемента, разположен във втория ред и втората колона. За нашата матрица тези елементи са равни на M11 = 0, M12 = 4, M21 = 6, M22 10. За колонен вектор тези стойности са равни на V11 = –2, V21 = 1. Според тази формула, получаваме следния резултат от произведението на квадратна матрица с вектор:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

За удобство нека напишем вектора на колоната в ред. И така, умножихме квадратната матрица по вектора (-2; 1), което доведе до вектора (4; -2). Очевидно това е същият вектор, умножен по λ = -2. Ламбда в този случай означава собствената стойност на матрицата.

Собствен вектор на матрица е колинеарен вектор, тоест обект, който не променя позицията си в пространството, когато се умножи по матрица. Концепцията за колинеарност във векторната алгебра е подобна на термина паралелизъм в геометрията. В геометрична интерпретация колинеарните вектори са успоредно насочени сегменти с различни дължини. От времето на Евклид знаем, че една права има безкраен брой успоредни прави, така че е логично да приемем, че всяка матрица има безкраен брой собствени вектори.

От предишния пример става ясно, че собствените вектори могат да бъдат (-8; 4), и (16; -8), и (32, -16). Всички те са колинеарни вектори, съответстващи на собствената стойност λ = -2. Когато умножим оригиналната матрица по тези вектори, пак ще получим вектор, който се различава от оригинала 2 пъти. Ето защо при решаването на задачи за намиране на собствен вектор е необходимо да се намират само линейно независими векторни обекти. Най-често за n × n матрица има n на брой собствени вектори. Нашият калкулатор е предназначен за анализ на квадратни матрици от втори ред, така че почти винаги резултатът ще намери два собствени вектора, с изключение на случаите, когато те съвпадат.

В примера по-горе знаехме собствения вектор на оригиналната матрица предварително и ясно определихме ламбда числото. На практика обаче всичко се случва обратното: първо се намират собствените стойности и едва след това собствените вектори.

Алгоритъм за решение

Нека погледнем оригиналната матрица M отново и се опитаме да намерим и двата й собствени вектора. Така че матрицата изглежда така:

• М = 0; 4;
• 6; 10.

Първо трябва да определим собствената стойност λ, което изисква изчисляване на детерминантата на следната матрица:

• (0 − λ); 4;
• 6; (10 − λ).

Тази матрица се получава чрез изваждане на неизвестното λ от елементите на главния диагонал. Детерминантата се определя по стандартната формула:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Тъй като нашият вектор трябва да е различен от нула, ние приемаме полученото уравнение като линейно зависимо и приравняваме нашата детерминанта detA към нула.

(0 − λ) × (10 − λ) − 24 = 0

Нека отворим скобите и да получим характеристичното уравнение на матрицата:

λ 2 − 10λ − 24 = 0

Това е стандартно квадратно уравнение, което трябва да се реши с помощта на дискриминант.

D = b 2 − 4ac = (-10) × 2 − 4 × (-1) × 24 = 100 + 96 = 196

Коренът на дискриминанта е sqrt(D) = 14, следователно λ1 = -2, λ2 = 12. Сега за всяка ламбда стойност трябва да намерим собствения вектор. Нека изразим коефициентите на системата за λ = -2.

• M − λ × E = 2; 4;
• 6; 12.

В тази формула E е матрицата на идентичност. Въз основа на получената матрица създаваме система от линейни уравнения:

2x + 4y = 6x + 12y,

където x и y са елементите на собствения вектор.

Нека съберем всички X отляво и всички Y отдясно. Очевидно - 4x = 8y. Разделете израза на - 4 и получете x = –2y. Сега можем да определим първия собствен вектор на матрицата, като вземем всякакви стойности на неизвестните (помнете безкрайността на линейно зависимите собствени вектори). Да вземем y = 1, тогава x = –2. Следователно първият собствен вектор изглежда като V1 = (–2; 1). Върнете се в началото на статията. Това беше този векторен обект, по който умножихме матрицата, за да демонстрираме концепцията за собствен вектор.

Сега нека намерим собствения вектор за λ = 12.

• M - λ × E = -12; 4
• 6; -2.

Нека създадем същата система от линейни уравнения;

• -12x + 4y = 6x − 2y
• -18x = -6y
• 3x = y.

Сега приемаме x = 1, следователно y = 3. Така вторият собствен вектор изглежда като V2 = (1; 3). При умножаване на оригиналната матрица по даден вектор, резултатът винаги ще бъде един и същ вектор, умножен по 12. Това е мястото, където алгоритъмът за решение завършва. Сега знаете как да определите ръчно собствения вектор на матрица.

• определител;
• следа, тоест сумата от елементите на главния диагонал;
• ранг, тоест максималният брой линейно независими редове/колони.

Програмата работи по горния алгоритъм, съкращавайки максимално процеса на решаване. Важно е да се отбележи, че в програмата ламбда се обозначава с буквата “c”. Нека да разгледаме числен пример.

Пример как работи програмата

Нека се опитаме да определим собствените вектори за следната матрица:

• М = 5; 13;
• 4; 14.

Нека въведем тези стойности в клетките на калкулатора и да получим отговора в следната форма:

• Ранг на матрицата: 2;
• Матрична детерминанта: 18;
• Следа на матрицата: 19;
• Изчисляване на собствения вектор: c 2 − 19.00c + 18.00 (характеристично уравнение);
• Изчисление на собствения вектор: 18 (първа ламбда стойност);
• Изчисление на собствения вектор: 1 (втора ламбда стойност);
• Система от уравнения за вектор 1: -13x1 + 13y1 = 4x1 − 4y1;
• Система от уравнения за вектор 2: 4x1 + 13y1 = 4x1 + 13y1;
• Собствен вектор 1: (1; 1);
• Собствен вектор 2: (-3,25; 1).

Така получихме два линейно независими собствени вектора.

Заключение

Линейната алгебра и аналитичната геометрия са стандартни предмети за всеки първокурсник по инженерство. Големият брой вектори и матрици е ужасяващ и е лесно да се направят грешки в такива тромави изчисления. Нашата програма ще позволи на учениците да проверят своите изчисления или автоматично да решат задачата за намиране на собствен вектор. В нашия каталог има и други калкулатори за линейна алгебра; използвайте ги в обучението или работата си.

"Първата част излага разпоредбите, които са минимално необходими за разбиране на хемометрията, а втората част съдържа фактите, които трябва да знаете за по-задълбочено разбиране на методите на многовариантния анализ. Презентацията е илюстрирана с примери, направени в работната книга на Excel Matrix.xls, който придружава този документ.

Връзките към примери се поставят в текста като Excel обекти. Тези примери са абстрактни и по никакъв начин не са свързани с проблемите на аналитичната химия. Примери от реалния живот за използване на матрична алгебра в хемометрията се обсъждат в други текстове, обхващащи различни хемометрични приложения.

Повечето измервания, направени в аналитичната химия, не са директни, а непряк. Това означава, че в експеримента вместо стойността на желания аналит С (концентрация) се получава друга стойност х(сигнал), свързан, но не равен на C, т.е. х(C) ≠ C. Като правило видът на зависимостта х(C) е неизвестен, но за щастие в аналитичната химия повечето измервания са пропорционални. Това означава, че с увеличаване на концентрацията на С в апъти, сигналът X ще се увеличи със същото количество, т.е. х(аВ) = a x(° С). В допълнение, сигналите също са адитивни, така че сигналът от проба, в която присъстват две вещества с концентрации C 1 и C 2, ще бъде равен на сумата от сигналите от всеки компонент, т.е. х(C 1 + C 2) = х(C 1)+ х(C 2). Пропорционалността и адитивността заедно дават линейност. Могат да се дадат много примери, за да се илюстрира принципът на линейността, но е достатъчно да се споменат двата най-ярки примера - хроматографията и спектроскопията. Втората особеност, присъща на експеримента в аналитичната химия е многоканален. Модерното аналитично оборудване измерва едновременно сигнали за много канали. Например, интензитетът на светлинното предаване се измерва за няколко дължини на вълната наведнъж, т.е. диапазон. Следователно в експеримента се занимаваме с много сигнали х 1 , х 2 ,...., х n, характеризираща съвкупността от концентрации C 1 , C 2 , ..., C m на веществата, присъстващи в изследваната система.

Ориз. 1 Спектри

И така, аналитичният експеримент се характеризира с линейност и многоизмерност. Следователно е удобно експерименталните данни да се разглеждат като вектори и матрици и да се манипулират с помощта на апарата на матричната алгебра. Плодотворността на този подход е илюстрирана от примера, показан в , който представя три спектъра, взети при 200 дължини на вълната от 4000 до 4796 cm-1. Първо ( х 1) и второ ( х 2) спектрите са получени за стандартни проби, в които са известни концентрациите на две вещества А и В: в първата проба [A] = 0,5, [B] = 0,1, а във втората проба [A] = 0,2, [ B] = 0,6. Какво може да се каже за нова, неизвестна проба, чийто спектър е посочен х 3 ?

Нека разгледаме три експериментални спектъра х 1 , х 2 и х 3 като три вектора с размерност 200. Използвайки линейна алгебра, човек може лесно да покаже това х 3 = 0.1 х 1 +0.3 х 2, така че третата проба очевидно съдържа само вещества А и В в концентрации [A] = 0,5×0,1 + 0,2×0,3 = 0,11 и [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Основна информация

1.1 Матрици

Матрицанаречена например правоъгълна таблица с числа

Ориз. 2 Матрица

Матриците се означават с главни удебелени букви ( А), а техните елементи - със съответните малки букви с индекси, т.е. а ij. Първият индекс номерира редовете, а вторият – колоните. В хемометриката е обичайно максималната стойност на индекса да се обозначава със същата буква като самия индекс, но с главни букви. Следователно матрицата Аможе да се запише и като ( а ij , аз = 1,..., аз; й = 1,..., Дж). За примерната матрица аз = 4, Дж= 3 и а 23 = −7.5.

Двойка числа азИ Джсе нарича размерност на матрицата и се означава като аз× Дж. Пример за матрица в хемометрията е набор от спектри, получени за азмостри за Дждължини на вълните.

1.2. Най-простите операции с матрици

Матриците могат да бъдат умножете по числа. В този случай всеки елемент се умножава по това число. Например -

Ориз. 3 Умножение на матрица по число

Две матрици с едно и също измерение могат да бъдат елемент по елемент гънкаИ извадете. Например,

Ориз. 4 Събиране на матрици

В резултат на умножение с число и събиране се получава матрица със същата размерност.

Нулевата матрица е матрица, състояща се от нули. Обозначава се О. Очевидно е, че А+О = А, А−А = Ои 0 А = О.

Матрицата може да бъде транспонирам. По време на тази операция матрицата се обръща, т.е. редовете и колоните се разменят. Транспонирането се обозначава с буква, А“ или индекс А T. По този начин, ако А = {а ij , аз = 1,..., аз; й = 1,...,Дж), Че А t = ( а джи , й = 1,...,Дж; i = 1,..., аз). Например

Ориз. 5 Транспониране на матрица

Очевидно е, че ( А t) t = А, (А+б) T = А t+ б T.

1.3. Матрично умножение

Матриците могат да бъдат умножават се, но само ако имат съответните размери. Защо това е така ще стане ясно от определението. Матричен продукт А, измерение аз× К, и матрици б, измерение К× Дж, се нарича матрица ° С, измерение аз× Дж, чиито елементи са числа

Така за продукта ABнеобходимо е броят на колоните в лявата матрица Абеше равен на броя на редовете в дясната матрица б. Пример за матричен продукт -

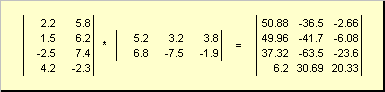
Фиг.6 Произведение на матрици

Правилото за матрично умножение може да се формулира по следния начин. За намиране на матричен елемент ° С, стоящ на кръстовището аз-ти ред и йта колона ( ° С ij) трябва да се умножава елемент по елемент аз-ти ред на първата матрица АНа йта колона на втората матрица би съберете всички резултати. Така че в показания пример елемент от третия ред и втората колона се получава като сбор от продуктите по елементи на третия ред Аи втора колона б

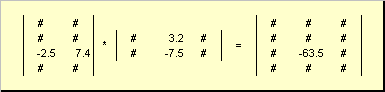
Фиг.7 Елемент от произведението на матрици

Продуктът на матриците зависи от реда, т.е. AB ≠ Б.А., поне поради размери. Казват, че е некомутативен. Продуктът на матриците обаче е асоциативен. Означава, че ABC = (AB)° С = А(пр.н.е.). Освен това е и разпределителен, т.е. А(б+° С) = AB+A.C.. Очевидно е, че А.О. = О.

1.4. Квадратни матрици

Ако броят на колоните на матрицата е равен на броя на нейните редове ( аз = J=N), тогава такава матрица се нарича квадратна. В този раздел ще разгледаме само такива матрици. Сред тези матрици могат да се разграничат матрици със специални свойства.

Нежененматрица (обозначена аз,и понякога д) е матрица, в която всички елементи са равни на нула, с изключение на диагоналните, които са равни на 1, т.е.

очевидно ИИ = И.А. = А.

Матрицата се нарича диагонал, ако всички негови елементи с изключение на диагоналните ( а ii) са равни на нула. Например

Ориз. 8 Диагонална матрица

Матрица Анаречен върхът триъгълна, ако всички негови елементи, лежащи под диагонала, са равни на нула, т.е. а ij= 0, при аз>й. Например

Ориз. 9 Горна триъгълна матрица

Долната триъгълна матрица се дефинира по подобен начин.

Матрица АНаречен симетричен, Ако А t = А. С други думи а ij = а джи. Например

Ориз. 10 Симетрична матрица

Матрица АНаречен ортогонален, Ако

А T А = А.А. t = аз.

Матрицата се нарича нормалноАко

1.5. Следа и определител

Следващияквадратна матрица А(означено с Tr( А) или Sp( А)) е сумата от неговите диагонални елементи,

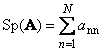
Например,

Ориз. 11 Матрична следа

Очевидно е, че

Sp(α А) = α Sp( А) И

Sp( А+б) = Sp( А)+ Sp( б).

Може да се покаже, че

Sp( А) = Sp( А t), Sp( аз) = н,

а също и това

Sp( AB) = Sp( Б.А.).

Друга важна характеристика на квадратната матрица е нейната детерминант(означен като det( А)). Определянето на детерминанта в общия случай е доста трудно, така че ще започнем с най-простия вариант - матрицата Аразмер (2×2). Тогава

За матрица (3×3) детерминантата ще бъде равна на

В случай на матрицата ( н× н) детерминантата се изчислява като сумата 1·2·3· ... · н= н! термини, всеки от които е равен

Индекси к 1 , к 2 ,..., к Нсе дефинират като всички възможни подредени пермутации rчислата в множеството (1, 2, ..., н). Изчисляването на детерминанта на матрица е сложна процедура, която на практика се извършва с помощта на специални програми. Например,

Ориз. 12 Матрична детерминанта

Нека отбележим само очевидните свойства:

det( аз) = 1, det( А) = det( А T),

det( AB) = det( А)дет( б).

1.6. Вектори

Ако матрицата се състои само от една колона ( Дж= 1), тогава се извиква такъв обект вектор. По-точно вектор колона. Например

Могат да се разглеждат и матрици, състоящи се от един ред, например

Този обект също е вектор, но редов вектор. Когато анализираме данни, е важно да разберем с кои вектори имаме работа - колони или редове. Така че спектърът, взет за една проба, може да се разглежда като ред вектор. Тогава наборът от спектрални интензитети при определена дължина на вълната за всички проби трябва да се третира като колонен вектор.

Размерността на вектора е броят на неговите елементи.

Ясно е, че всеки колонен вектор може да бъде превърнат във вектор на ред чрез транспониране, т.е.

В случаите, когато формата на вектора не е конкретно определена, а просто се казва, че е вектор, тогава те означават колонен вектор. Ние също ще се придържаме към това правило. Векторът се обозначава с малка, изправена, удебелена буква. Нулев вектор е вектор, чиито всички елементи са нула. Обозначава се 0 .

1.7. Най-простите операции с вектори

Векторите могат да се добавят и умножават по числа по същия начин като матриците. Например,

Ориз. 13 Операции с вектори

Два вектора хИ гса наречени колинеарен, ако има число α такова, че

1.8. Продукти от вектори

Два вектора с едно и също измерение нможе да се умножи. Нека има два вектора х = (х 1 , х 2 ,...,х N)t и г = (г 1 , г 2 ,...,г N) t . Ръководейки се от правилото за умножение ред по колона, можем да съставим две произведения от тях: х T гИ xy T. Първа работа

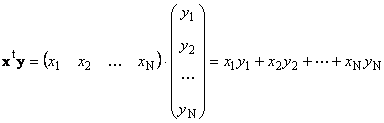
Наречен скаларенили вътрешни. Резултатът му е число. Означава се също с ( х,г)= х T г. Например,

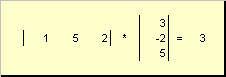
Ориз. 14 Вътрешно (скаларно) произведение

Второ парче

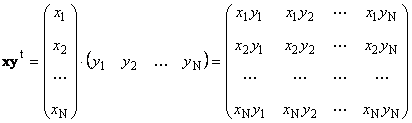
Наречен външен. Неговият резултат е матрица на измерение ( н× н). Например,

Ориз. 15 Външна работа

Наричат ​​се вектори, чието скаларно произведение е нула ортогонален.

1.9. Векторна норма

Скаларното произведение на вектор със себе си се нарича скаларен квадрат. Тази стойност

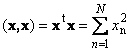
определя квадрат дължинавектор х. За да посочите дължина (наричана още норматавектор) се използва обозначението

Например,

Ориз. 16 Векторна норма

Вектор на единична дължина (|| х|| = 1) се нарича нормализиран. Ненулев вектор ( х ≠ 0 ) може да се нормализира, като се раздели на дължина, т.е. х = ||х|| (х/||х||) = ||х|| д. Тук д = х/||х|| - нормализиран вектор.

Векторите се наричат ​​ортонормални, ако всички те са нормализирани и ортогонални по двойки.

1.10. Ъгъл между векторите

Скаларното произведение определя и ъгълφ между два вектора хИ г

Ако векторите са ортогонални, тогава cosφ = 0 и φ = π/2, а ако са колинеарни, тогава cosφ = 1 и φ = 0.

1.11. Векторно представяне на матрица

Всяка матрица Аразмер аз× Джможе да се представи като набор от вектори

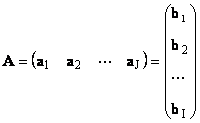
Тук всеки вектор а йе йта колона и вектора на реда b азе азред на матрицата А

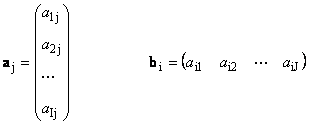
1.12. Линейно зависими вектори

Вектори с едно и също измерение ( н) могат да се добавят и умножават по число, точно като матриците. Резултатът ще бъде вектор със същото измерение. Нека има няколко вектора с еднаква размерност х 1 , х 2 ,...,х K и същия брой числа α α 1 , α 2 ,...,α К. вектор

г= α 1 х 1 + α 2 х 2 +...+ α К х К

Наречен линейна комбинациявектори х к .

Ако има такива ненулеви числа α к ≠ 0, к = 1,..., К, Какво г = 0 , тогава такъв набор от вектори х кНаречен линейно зависими. В противен случай се казва, че векторите са линейно независими. Например вектори х 1 = (2, 2)t и х 2 = (−1, −1) t са линейно зависими, т.к х 1 +2х 2 = 0

1.13. Ранг на матрицата

Помислете за набор от Квектори х 1 , х 2 ,...,х Кразмери н. Рангът на тази система от вектори е максималният брой линейно независими вектори. Например в комплекта

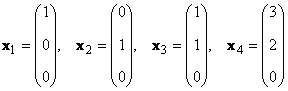
има само два линейно независими вектора, например х 1 и х 2, така че рангът му е 2.

Очевидно, ако има повече вектори в набор от тяхното измерение ( К>н), тогава те задължително са линейно зависими.

Ранг на матрицата(означено с ранг( А)) е рангът на системата от вектори, от които се състои. Въпреки че всяка матрица може да бъде представена по два начина (вектори в колона или ред), това не влияе на стойността на ранга, т.к.

1.14. обратна матрица

Квадратна матрица Асе нарича неизроден, ако има уникален обратенматрица А-1, определени от условията

А.А. −1 = А −1 А = аз.

Обратната матрица не съществува за всички матрици. Необходимо и достатъчно условие за неизраждане е

det( А) ≠ 0 или ранг( А) = н.

Обръщането на матрицата е сложна процедура, за която има специални програми. Например,

Ориз. 17 Инверсия на матрицата

Нека представим формулите за най-простия случай - матрица 2×2

Ако матрици АИ бтогава са неизродени

(AB) −1 = б −1 А −1 .

1.15. Псевдообратна матрица

Ако матрицата Ае сингулярен и обратната матрица не съществува, тогава в някои случаи можете да използвате псевдообратноматрица, която се определя като такава матрица А+ това

А.А. + А = А.

Псевдообратната матрица не е единствената и нейната форма зависи от метода на конструиране. Например за правоъгълна матрица можете да използвате метода на Мур-Пенроуз.

Ако броят на колоните е по-малък от броя на редовете, тогава

А + =(А T А) −1 А T

Например,

Ориз. 17а Псевдоинверсия на матрица

Ако броят на колоните е по-голям от броя на редовете, тогава

А + =А T( А.А. T) −1

1.16. Умножение на вектор по матрица

вектор хможе да се умножи по матрица Аподходящ размер. В този случай векторът на колоната се умножава отдясно брадва, а векторният ред е отляво х T А. Ако векторното измерение Дж, и размерността на матрицата аз× Джтогава резултатът ще бъде вектор на измерение аз. Например,

Ориз. 18 Умножение на вектор по матрица

Ако матрицата А- квадрат ( аз× аз), след това векторът г = брадваима същото измерение като х. Очевидно е, че

А(α 1 х 1 + α 2 х 2) = α 1 брадва 1 + α 2 брадва 2 .

Следователно матриците могат да се разглеждат като линейни трансформации на вектори. В частност Ix = х, вол = 0 .

2. Допълнителна информация

2.1. Системи линейни уравнения

Позволявам А- размер на матрицата аз× Дж, А b- размерен вектор Дж. Помислете за уравнението

брадва = b

спрямо вектора х, размери аз. По същество това е система от азлинейни уравнения с Джнеизвестен х 1 ,...,х Дж. Решение съществува тогава и само ако

ранг ( А) = ранг ( б) = Р,

Където бе разширена матрица от измерения аз×( J+1), състоящ се от матрица А, допълнена с колона b, б = (А b). В противен случай уравненията са непоследователни.

Ако Р = аз = Дж, тогава решението е уникално

х = А −1 b.

Ако Р < аз, тогава има много различни решения, които могат да бъдат изразени чрез линейна комбинация Дж−Рвектори. Система от еднородни уравнения брадва = 0 с квадратна матрица А (н× н) има нетривиално решение ( х ≠ 0 ) ако и само ако det( А) = 0. Ако Р= ранг( А)<н, тогава има н−Рлинейно независими решения.

2.2. Билинейни и квадратични форми

Ако Ае квадратна матрица и хИ г- вектор на съответната размерност, след това скаларното произведение на формата х T даНаречен билинеенформа, определена от матрица А. При х = гизразяване х T брадваНаречен квадратнаформа.

2.3. Положително определени матрици

Квадратна матрица АНаречен положително определено, ако за всеки ненулев вектор х ≠ 0 ,

х T брадва > 0.

По подобен начин се определя отрицателен (х T брадва < 0), неотрицателни (х T брадва≥ 0) и отрицателен (х T брадва≤ 0) определени матрици.

2.4. Разлагане на Холецки

Ако симетричната матрица Ае положително определена, тогава има уникална триъгълна матрица Uс положителни елементи, за които

А = U T U.

Например,

Ориз. 19 Разлагане на Холецки

2.5. Полярно разлагане

Позволявам Ае неособена квадратна матрица с размерност н× н. След това има уникален поляренпроизводителност

А = С.Р.

Където Се неотрицателна симетрична матрица и Ре ортогонална матрица. Матрици СИ Рможе да се дефинира изрично:

С 2 = А.А. t или С = (А.А. t) ½ и Р = С −1 А = (А.А. t) −½ А.

Например,

Ориз. 20 Полярно разлагане

Ако матрицата Ае изродено, тогава разлагането не е уникално - а именно: Свсе още сама, но Рможе би много. Полярното разлагане представлява матрицата Акато комбинация от компресия/удължаване Си се обърнете Р.

2.6. Собствени вектори и собствени стойности

Позволявам Ае квадратна матрица. вектор vНаречен собствен векторматрици А, Ако

Av = λ v,

където се нарича числото λ собствена стойностматрици А. По този начин трансформацията, която матрицата извършва Анад вектора v, се свежда до просто разтягане или компресия с коефициент λ. Собственият вектор се определя до умножение с константа α ≠ 0, т.е. Ако vе собствен вектор, тогава α v- също собствен вектор.

2.7. Собствени стойности

В матрицата А, измерение ( н× н) не може да бъде повече от нсобствени стойности. Те задоволяват характеристично уравнение

det( А − λ аз) = 0,

което е алгебрично уравнение н-та поръчка. По-специално, за матрица 2 × 2 характеристичното уравнение има формата

Например,

Ориз. 21 собствени стойности

Набор от собствени стойности λ 1 ,..., λ нматрици АНаречен спектър А.

Спектърът има различни свойства. В частност

det( А) = λ 1 ×...×λ н,Sp( А) = λ 1 +...+λ н.

Собствените стойности на произволна матрица могат да бъдат комплексни числа, но ако матрицата е симетрична ( А t = А), тогава неговите собствени стойности са реални.

2.8. Собствени вектори

В матрицата А, измерение ( н× н) не може да бъде повече от нсобствени вектори, всеки от които съответства на собствената си стойност. За определяне на собствения вектор v нтрябва да се реши система от еднородни уравнения

(А − λ н аз)v н = 0 .

Има нетривиално решение, тъй като det( А −λ н аз) = 0.

Например,

Ориз. 22 Собствени вектора

Собствените вектори на симетрична матрица са ортогонални.