Elektrisches Feld einer gleichmäßig geladenen Ebene. Anwendung des Gaußschen Theorems zur Berechnung des Feldes einer unendlichen, gleichmäßig geladenen Ebene

Zuvor haben wir das gezeigt elektrisches Feld, erzeugt durch eine unendliche, gleichmäßig geladene Platte, ist homogen, das heißt, die Feldstärke ist an allen Punkten gleich, und der Intensitätsvektor ist senkrecht zur Ebene gerichtet und sein Modul ist gleich E o = σ/(2ε o). Die Kraftlinienschar eines solchen Feldes besteht aus einer Reihe paralleler Linien senkrecht zur Platte. In Abb. 275, 276 zeigt auch eine grafische Darstellung der Projektion des Feldstärkevektors Ez pro Achse Z senkrecht zur Platte (wir werden den Ursprung dieser Achse auf der Platte platzieren). Es ist klar, dass das Potenzial dieses Feldes nur von der Koordinate abhängt z, das heißt, die Äquipotentialflächen sind in diesem Fall Ebenen parallel zur geladenen Platte.



Reis. 275



Reis. 276
Mit der traditionellen Wahl des Nullpotentialniveaus φ(z → ∞), das Potential eines beliebigen Punktes ist gleich der Arbeit, eine positive Einheitsladung von einem gegebenen Punkt ins Unendliche zu bewegen. Da der Spannungsmodul konstant ist, ist diese Arbeit (und damit das Potenzial) gleich unendlich! Folglich ist die angegebene Wahl des Nullpotentialniveaus in diesem Fall ungeeignet.
Daher sollten Sie die Willkür bei der Wahl des Nullniveaus ausnutzen. Es reicht aus, einen beliebigen Punkt mit Koordinaten auszuwählen z = z o und weisen Sie ihm einen beliebigen potentiellen Wert zu φ(z o) = φ o(Abb. 277).

Reis. 277
Berechnen Sie nun den potenziellen Wert an einem beliebigen Punkt φ(z), können Sie den Zusammenhang zwischen Feldstärke und Potenzial nutzen

Bedenkt man, dass in diesem Fall die Feldstärke konstant ist (bei z > 0) wird dieser Ausdruck in der Form geschrieben

Daraus folgt die gewünschte Abhängigkeit des Potentials von der Koordinate (bei z > 0)

Insbesondere können Sie einen beliebigen Wert des Potentials der Platte selbst einstellen, also auf einstellen z = z o = 0, φ = φ o. Dann wird der Wert des Potentials an einem beliebigen Punkt durch die Funktion bestimmt

Der Graph davon ist in Abbildung 278 dargestellt.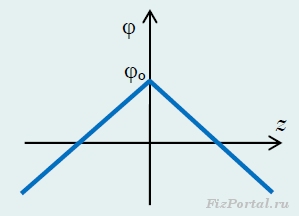

Reis. 278
Dass das Potential relativ zur Unendlichkeit unendlich groß ausfiel, liegt auf der Hand – schließlich hat eine unendliche Platte auch eine unendlich große Ladung. Wie wir bereits betont haben, handelt es sich bei einem solchen System um eine Idealisierung – unendliche Platten existieren nicht. In Wirklichkeit haben alle Körper endliche Abmessungen, sodass für sie die traditionelle Wahl des Nullpotentials möglich ist, obwohl in diesem Fall die Feldverteilung sehr komplex sein kann. Im Rahmen der betrachteten Idealisierung ist es bequemer, die von uns verwendete Wahl des Nullniveaus zu verwenden.

Finden wir die Verteilung des Feldpotentials, das von zwei identischen, gleichmäßig geladenen parallelen Platten erzeugt wird, deren Ladungen gleich groß und im Vorzeichen 1 entgegengesetzt sind (Abb. 279).

Reis. 279
Bezeichnen wir die Oberflächenladungsdichte auf einer Platte +σ , und auf der anderen Seite −σ . Abstand zwischen den Platten H Wir gehen davon aus, dass es deutlich kleiner ist als die Größe der Platten. Lassen Sie uns ein Koordinatensystem einführen, eine Achse z der senkrecht zu den Platten steht, wird der Koordinatenursprung in der Mitte zwischen den Platten platziert. Offensichtlich hängen bei unendlich großen Platten alle Feldeigenschaften (Stärke und Potential) nur von der Koordinate ab z. Um die Feldstärke an verschiedenen Punkten im Raum zu berechnen, verwenden wir den resultierenden Ausdruck für die Feldstärke, die durch eine unendliche, gleichmäßig geladene Platte erzeugt wird, und das Superpositionsprinzip.
Jede gleichmäßig geladene Platte erzeugt ein gleichmäßiges Feld, dessen Modul gleich ist E o = σ/(2ε o), und die Richtungen sind in Abbildung 280, 281 angegeben.



Reis. 280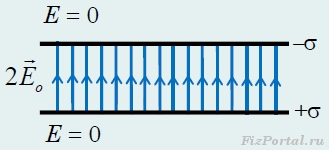

Reis. 281
Addiert man die Feldstärken nach dem Superpositionsprinzip, erhält man die Feldstärke im Raum zwischen den Platten E = 2E o = σ/ε o die doppelte Feldstärke einer Platte (hier sind die Felder der einzelnen Platten parallel), und es gibt kein Feld außerhalb der Platten (hier sind die Felder der einzelnen Platten entgegengesetzt).
Streng genommen ist das Feld für Platten endlicher Größe nicht gleichmäßig; die Feldlinien der Platten endlicher Größe sind in Abbildung 282 dargestellt.



Reis. 282
Die stärksten Abweichungen von der Homogenität werden in der Nähe der Plattenränder beobachtet (häufig werden diese Abweichungen als „Abweichungen“ bezeichnet). Kanteneffekte). Im Bereich neben der Plattenmitte kann das Feld jedoch mit hoher Genauigkeit als homogen angesehen werden, d. h. in diesem Bereich können Randeffekte vernachlässigt werden. Beachten Sie, dass die Fehler in dieser Näherung umso kleiner sind, je kleiner das Verhältnis des Abstands zwischen den Platten zu ihrer Größe ist.
Um die Verteilung des Feldpotentials eindeutig zu bestimmen, ist es notwendig, den Pegel des Nullpotentials zu wählen. Wir gehen davon aus, dass das Potential in der Ebene in der Mitte zwischen den Platten gleich Null ist, das heißt, wir setzen φ = 0 bei z = 0.
Trotz der Willkür bei der Wahl des Nullpotentialniveaus kann unsere Wahl auf der Grundlage der Symmetrie des Systems logisch begründet werden. Tatsächlich wiederholt sich das betrachtete Ladungssystem in Spiegelung relativ zur Ebene z = 0 und ein gleichzeitiger Wechsel der Vorzeichen der Ladungen. Daher ist es wünschenswert, dass die Potentialverteilung die gleiche Symmetrie aufweist: Sie wird bei Spiegelreflexion mit gleichzeitigem Vorzeichenwechsel aller Feldfunktionen wiederhergestellt. Die von uns gewählte Methode zur Auswahl des Nullpotentials erfüllt diese Symmetrie.



Reis. 283
Bezeichnen wir das Potential einer positiv geladenen Platte +φo, dann ist das Potential der negativ geladenen Platte gleich φ o. Diese Potenziale können anhand des ermittelten Werts der Feldstärke zwischen den Platten und des Zusammenhangs zwischen der Stärke und der Potenzialdifferenz leicht ermittelt werden elektrisches Feld. Die Gleichung dieser Verbindung hat in diesem Fall die Form +φo − φ o = Eh. Aus dieser Beziehung ermitteln wir die Werte der Plattenpotentiale φ o = σh/(2ε o). Wenn man bedenkt, dass das Feld zwischen den Platten gleichmäßig ist (daher ändert sich das Potential linear) und es außerhalb der Platten kein Feld gibt (daher ist das Potential hier konstant), ergibt sich die Abhängigkeit des Potentials von der Koordinate z sieht aus wie (Abb. 284)

Reis. 284

 Aufgaben für selbstständiges Arbeiten.
 1. Führen Sie in allen betrachteten Beispielen den umgekehrten Vorgang durch: Verwenden Sie die gefundene Potenzialverteilung mithilfe der Formel E x = −Δφ/Δx Berechnen Sie die Stärken der betrachteten Felder.
 2. Leiten Sie Formel (6) streng her.
 3. Erklären Sie qualitativ das folgende „Paradoxon“. Im Bereich eines Flachkondensators ist das „Unendlichkeits“-Potential mehrdeutig definiert: bei Bewegung in positiver Richtung der Achse Z Das Potenzial der „Unendlichkeit“ erwies sich als gleich −φo; bei Bewegung in negativer Achsrichtung Z − +φo, wenn man sich entlang der Achsen bewegt X oder Y− ist gleich Null. Was ist also das Potenzial von „Unendlichkeit“ in einem realen System aus zwei Platten endlicher Größe?

1 Ein solches System heißt Flachkondensator, wir werden diese Geräte später genauer untersuchen.

Nehmen wir an, die Ladung ist positiv. Die Ebene wird mit einer konstanten Oberflächendichte aufgeladen. Aus der Symmetrie folgt, dass die Intensität an jedem Punkt des Feldes eine Richtung senkrecht zur Ebene hat (Abb. 2.10). Es ist offensichtlich, dass an Punkten, die relativ zur Ebene symmetrisch sind, die Feldstärke gleich groß und entgegengesetzt gerichtet ist.

Wählen wir einen Bereich auf der geladenen Ebene aus. Lassen Sie uns diesen Bereich mit einer geschlossenen Fläche umgeben. Als geschlossene Fläche stellen wir uns eine zylindrische Fläche mit Erzeugenden senkrecht zur Ebene und Größenbasen vor, die symmetrisch zur Ebene angeordnet sind. Wenden wir den Satz von Gauß auf diese Fläche an . Es findet keine Strömung durch die Seite der Oberfläche statt, da sie an jedem Punkt Null ist. Für Basen dasselbe wie . Daher ist der Gesamtfluss durch die Oberfläche gleich. Im Inneren der Oberfläche befindet sich eine Ladung. Nach dem Satz von Gauß muss folgende Bedingung erfüllt sein: , Wo . (3)

Das erhaltene Ergebnis hängt nicht von der Länge des Zylinders ab, d. h. In jedem Abstand von der Ebene ist die Feldstärke gleich groß. Das Bild der Spannungslinien sieht wie in Abb. 2.11. Bei einer negativ geladenen Ebene ändern sich die Richtungen der Vektoren in die entgegengesetzte Richtung. Wenn die Ebene endliche Abmessungen hat, ist das erhaltene Ergebnis nur für Punkte gültig, deren Abstand vom Rand der Platte den Abstand von der Platte selbst deutlich übersteigt (Abb. 2.12).