At the center of a metal hollow sphere whose radius is

Rice. 1.93
b)
A)
f! = ,ф2 = th-.
Since the balls are connected by a conductor, then phx = (p2 = ph. Therefore, Df
= k And d2 =
g f ft "
Surface charge densities of the balls, respectively
are equal:
_f_ _f
,2 4l/gDia2 4nkr"
4 kR
Since R g, then a2 Or, i.e., the surface charge density on a small ball, the curvature of which is large (at the tip), is significantly greater than the surface charge density on a large ball, the curvature of which is small.
Problem 4
A small ball is connected by a wire to a grounded electrometer (see Fig. 1.87). By touching the ball to various points of the conductor, bounded by cylindrical and conical surfaces, the same deflection of the electrometer needle is observed at any position of the ball. Then the connecting wire is removed and it is observed that the deflection of the electrometer needle, to the rod of which the ball is brought, is not the same and depends on which point on the surface of the conductor (internal or external) was previously touched by the ball. Why?
Solution. An electrometer measures the potential difference between a given body and the ground. Since the surface of the conductor is equipotential, in the first case the arrow deviates by the same angle at any position of the ball.
In the second case, the deflection of the needle is determined by the potential of the ball relative to the ground at the moment when it is brought into contact with the electrometer. This potential depends on the charge of the ball, its size and the location of surrounding objects. At the moment the ball comes into contact with the conductor, its potential becomes equal to the potential of the conductor, but its charge will depend on which part of the surface is touched. If they touch the inner conical surface conductor, then the charge of the ball is zero, since the entire charge of the conductor is distributed over its outer surface. If the ball touches the outer surface of the conductor, then the charge of the ball will be different from zero.
As the ball moves, its potential continuously changes, as the position of the ball relative to surrounding objects changes. Various meanings The potential of the ball at the moment of its contact with the electrometer rod is determined only by the difference in the values ​​of the charge of the ball, since the location of surrounding objects relative to it at this moment is unchanged.
The maximum charge will be at the top of the conical surface (point).
Problem 5 An uncharged metal ball of radius r is surrounded by a concentric conducting sphere of radius R. The sphere is charged to potential φ0 (relative to the ground). What will the potential of the outer sphere be equal to if the uncharged ball is grounded (Fig. 1.94)?

Solution. Before grounding, the charge q of the outer sphere creates a potential on its surface
φ0 = kj^. After grounding on the internal
the ball will be induced with a charge q1 (see Fig. 1.94), which can be found from the condition that the potential of the grounded ball is zero.
According to the principle of superposition of fields Fig. 1.94 the potential of the ball is:
0.
Hence, the potential on the outer sphere after grounding the ball is created by charges q and
R-g
R
Fo-? The positive charge +d0 is uniformly distributed over a thin wire ring of radius R. In the center of the ring there is a point charge -d, the mass of which is m. This charge is given an initial velocity uQ along the axis of the ring. Determine the nature of the motion of the charge, depending on the initial speed, assuming that it moves along the axis of the ring. The ring is motionless.
Solution. The total energy of the charge at the initial moment is equal to
2
mv0
amount kinetic energy-and potential energy in
electrostatic field of the ring -Ф0д, where Ф0 = k-^ is the potential in the center of the ring:
2

At W > O the charge goes to infinity. Moreover, its speed is infinite long distance will be equal to zero if W = 0. If W > 0, the speed of the charge at an infinitely large distance from the ring is equal to:

If W 2
mv0 ,qq0 and Mo

A solitary metal ball of radius A = 10 cm is surrounded by a dielectric (є = 2). The dielectric forms a spherical layer with radii = 10 cm and D2 = 20 cm. Find the potential
ball if its charge q = 10-18 C.
Solution. The dielectric surrounding the ball becomes polarized under the action of the ball's field. As a result, on inner surface In the dielectric, a polarization charge -q appears, the sign of which is opposite to the sign of the ball charge q, and on the outer surface of the dielectric there is a polarization charge q, identical in sign to the charge q. Consequently, the potential of the ball, according to the principle of superposition, is equal to the sum of the potentials of the fields formed by charges q, -q" and q":
Since the polarization charge (see problem 7 in § 1.16) is equal to:
._g(e ~ 1)
That
Exercise 3
Point charges q1 = 2 10~8 C and q2 = 10~8 C are located in kerosene (є = 2.1) at a distance rx = 0.04 m from each other. How much work must be done to bring the charges closer to a distance r2 = 0.02 m?
The field is formed by point charges q1 = -2 10~9 C and q2 = 10-9 C, located at a distance BC - 8 cm (Fig. 1.95). Point D lies on the perpendicular
line drawn to segment BC through its
the middle of M, with MD = BC/2. Find-i
those jobs Coulomb forces when changing - V 1?
charge q = 2 10-8 C from point D % i m І2
to point M. Fig. 1.95 A speck of dust with a mass m = 10-11 g is suspended in a uniform electric field between horizontally located differently charged plates, the distance between which is d = 5 mm. A speck of dust is illuminated ultraviolet light and as a result loses charge. In this case, the equilibrium of the dust particle is disturbed. How much charge did the dust particle lose if initially a voltage u = 154 V was applied to the plates, and then, in order to restore the equilibrium of the dust particle, it was necessary to increase the voltage by U2 = 8 V?
Two balls have the same electric charges q = = 20 nC. The balls are connected with thin wire. What charge will pass through the wire if the balls are metal and their radii are respectively = 15 cm and R2 = 5 cm? The distance between the balls is much greater than their radii.
N identical spherical drops of mercury are charged in the same way to the same potential fg. What is the potential f of a large drop of mercury resulting from the merger of these drops?
Two namesake point charge q1 and q2 with masses m1 and mn2 move towards each other. At the moment of time when the distance between the charges is equal to r1, they have velocities v1 and v2. To what minimum distance r2 will the charges approach each other?
Two small similarly charged balls are fixed in a vacuum at a distance significantly greater than their linear dimensions. If you release the first ball, then when the distance r between the balls is reached, its speed is v1 = 3 m/s; if you let go of the second one, then
Under the same conditions, its speed turns out to be equal to v2 = 4 m/s. Find the speed of the balls when they move apart by a distance r, if both balls are released at the same time.
At some point in time, two electrons had equal velocities v1 = v2 = v and were in vacuum at a distance L from each other. In this case, the velocities and v2 formed equal sharp corners and with a straight line connecting the electrons. Which minimum distance will the electrons pass relative to each other?
A particle of mass m, having a charge q and a speed vQ, approaches a charged, loose ring from a large distance, moving along its axis. Ring radius R, charge Q, mass M. What speed will the particle have at the moment when it passes through the center of the ring?
A small metal ball with a mass m - 1 g, which is given a charge q = 10~7 C, is thrown from afar with a speed v = 1 m/s in the direction of a metal sphere having a charge Q = 3 10~7 C. At what minimum radius of the sphere will the ball reach its surface?
Two homogeneous electric fields with horizontally and vertically directed intensities act simultaneously in space, the modules of which are equal to Er = 4,102 V/m and Ev = 3,102 V/m, respectively. In the direction of the force line of the resulting electric field, an electron flies in, the speed of which changes by a factor of 2 along the path L = 2.7 mm. Determine the speed of the electron at the end of this path.
Three identical charge, each of which is equal to q = -2 10-8 C, are located at the vertices of an equilateral triangle with side a = 10 cm. How much work A must be done to move one of them to the middle of the opposite side?
Point charges qx = -1.7 10_8Cl2 = 2 10-8 C are located from the point charge q0 = 3 10-8 C at a distance of 1X = 2 cm and 12 = 5 cm, respectively. How much work A must be done to swap the places of charges qx and d2?
Three conducting concentric spheres have radii R, 2R, 3R respectively. The middle sphere has a charge of +q. There is a hole made in it through which the outer and inner spheres are connected with a thin wire. Determine the charge qj of the outer sphere after connection.
Two conducting spheres are charged so that the inner one has a potential q>p and the outer one φ2. What potential will the inner sphere have if both spheres are connected by a conductor?
A metal ball with a radius = 2 cm carries a charge = 4 10-8 C. The ball is surrounded by a concentric conducting shell of radius R2 = 5 cm, the charge of which is q2 = -4 10~8 C. Determine the field potential φ at a distance L = 4 cm from the center of the ball.
A metal ball with radius R1 = 1 cm carries a charge q1 = 2 10-8 C. The ball is surrounded by a concentric conducting shell of radius R2 = 5 cm. The shell contains a charge q2 = -4 10-8 C. Find the change in the ball potential Af if the shell is grounded.
Four identical charged small balls, charges q and masses m, are located at the vertices of a square with side a. Which maximum speed will the balls reach if they are released?
A point charge +q moves from infinity to a metal plate. Determine the energy of interaction between the charge and the plate, as well as the speed of the charge at the moment when it is at a distance d from the plate. Being at an infinitely large distance from the plate, the charge had a speed equal to zero.
Four identical point charges q are located along a straight line at a distance I from each other. How much work must be done to place them at the vertices of a regular tetrahedron with an edge equal to Z?

Subject. Solving problems on the topic "Electrostatics. Electric field in a vacuum."

Consider electric field stationary charges;

Introduce the main characteristics of the electrostatic field: intensity and potential; find out the physical meaning of these quantities;

Show, using several examples, methods for solving problems for calculating the main characteristics of the electric field.

Progress of the lesson

During the lesson, it is necessary to consider a number of qualitative problems and then solve several calculation problems as their complexity increases.

When solving problems about the interaction of charges, it is necessary to make a drawing, indicating on it all the forces acting on the charge.

If the charge is stationary, write down the equilibrium conditions.

If the charge is moving, write down the equation of motion.

When solving problems about the work of electric field forces on charges, one should write down equations that take into account the conservation and transformation of energy during the interaction of charged bodies. It should be noted that solving problems in electrostatics requires knowledge not only of the laws of the electric field, but also the laws of mechanics.

Qualitative tasks

1. There is a positively charged ball. How can you use this ball, without reducing its charge, to electrify two other balls - one positively, the other negatively?

2. Why are conductors used in electrostatic experiments made hollow?

3. Two completely identical elderberry balls are suspended on thin silk threads: one is charged, and the other is uncharged. How to determine which ball is charged if no other devices or materials are given?

4. There is a hollow conducting uncharged sphere, inside of which a positively charged ball is placed.

a) Indicate where electric fields will exist.

b) Will charges appear on the sphere?

c) Will the field change inside and outside the sphere if you move the ball; what if the ball is left motionless and a charged body is brought outside to the sphere?

5. If you charge conductor A, then induced charges arise on conductor B, but if you charge conductor B, then induced charges do not arise on conductor A. In what case is this observed?

6. What is the field strength at the center of a uniformly charged wire ring shaped like a circle? At the center of a uniformly charged spherical surface?

7. In what case, when two similarly charged bodies approach each other, does the repulsive force between them decrease to zero?

8. Will the electric field strength between two oppositely charged planes change if the distance between them is doubled?

9. Two intersecting planes are uniformly charged with a negative charge. A radioactive source is placed at a certain point between the planes. Draw an approximate view of the trajectories of positively and negatively charged particles emitted by the source. What are these curves?

10. How can you change the potential of a conductor without touching it or changing its charge?

11. Compare the work on moving a charge in the electrostatic field of a positive point charge from point A to B and from A to C (Fig. 1) and justify your answer.

12. If metal balls having different diameters are given equal negative charges, will current flow in the wire that connects the balls after they are charged?

13. There are two conductors, one of them has less charge, but the potential is higher than the other. How will electric charges move when conductors touch?

14. Can an electrostatic field exist in a vacuum, the intensity vector of which has the same direction throughout the entire volume, and perpendicular to this direction changes its value according to a linear law (Fig. 2)?

Examples of solving calculation problems

Task 1. Along a thin wire ring of radius R charge is evenly distributed q. Find the electric field strength and potential at an arbitrary point lying on a perpendicular restored to the plane of the ring, at the center of the ring.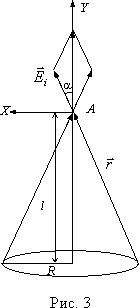

Solution:

To solve the problem, we will use the superposition principle for electric fields. Let us mentally divide the ring into sections whose linear dimensions are much less than the distance from this section to the point A, in which the potential and electric field strength are calculated.

We will assume that the ring has a positive charge. Let us denote by l distance from the center of the ring to the point A, and through r- distance from the selected area to the point A(Fig. 3). Field potential at a point A, created by one small section of the ring with the number i will be equal to , where is the charge of this section.

Potential at a point A, created by a charged ring, according to the superposition principle for electric fields, will be equal to

Finally we get:

The field strength created by the charge of the section with number i, will be equal

where is the radius vector defining the position of the point A relative to the area with number i. Let us select another section lying at the other end of the diameter of the ring drawn through the section with number i. The field strength vector created by this section will be the same in magnitude, but different in direction. In this case, both vectors make the same angle with the axis X, coinciding with the axis of the ring. If we project these vectors onto the axes X And Y, then the resulting projection onto the axis X will be equal to zero. These arguments are valid for any two sections lying at opposite ends of the diameter. This means that the resulting vector of tension at the point A will be directed along the axis Y. The magnitude of the vector can be found by adding the projections onto the axis Y tension vectors created by all sections of the ring.

From geometric considerations it is clear that . Then the modulus of the tension vector at a point separated by a distance l from the center of the ring, will be equal

If the point A is very far from the ring, that is l >> R, the expression for the field strength will have the following form:

that is, the field strength will be equal to the field strength of the point charge.

If l= 0, then E= 0, the field strength at the center of a uniformly charged ring is zero.

Answer:

Task 2. Particle of mass m, having a charge q, moves along the axis of the charged ring, approaching it. Which lowest speed v must the particle be at a very large distance from the ring in order to fly through it? Ring weight M, its radius R, and the charge is Q. The ring is not secured.

Solution:

To fly through the ring, it is enough to reach its center at a speed equal speed rings. Let us use the law of conservation of momentum for the charge-ring system. In the initial state, the ring is motionless; in the final state, the ring and the charge move as one with speed , therefore,

The forces acting on the charge-ring system are potential, therefore the law of conservation of energy must be satisfied. At the initial moment, the distance between the charge and the ring, according to the conditions of the problem, is very large, therefore the potential energy of their interaction is zero. When the charge is at the center of the ring, the potential interaction energy will be equal to

where is the potential at the center of the ring, equal to (see problem 1).

Then the law of conservation of energy will be written as follows:

(2)

Solving (1) and (2) together, we obtain

Answer:

Task 3. On distance R there is a point charge from the center of an uncharged metal ball q. Determine the potential of the ball.

Solution:

The metal ball is a conductor. The ball is in the electric field of a charge q. Under the influence of this field, the charges are redistributed along the conductor so that the potential of all points on the ball is the same. Therefore, to solve the problem it is enough to find the potential of one point on the ball.

The easiest way to find the field potential is at the center of the ball. It is equal to the sum of the potentials created at this point by the charge q and charges induced on the surface of the ball. The surface of the ball can be divided into elementary sections, the linear dimensions of which are much smaller than the radius of the ball. Then the potential at the center of the ball is determined by the expression

where is the potential created by one elementary section:

here is the charge of the selected area, r- radius of the ball. Since the ball is not charged, then the potential of the ball will be equal to

Answer:

Task 4. In the middle flat capacitor, charged to voltage U, there is a small metal ball of radius r. What charge will appear on the ball if it is connected by a conductor to one of the plates? Neglect the redistribution of charge along the capacitor plates under the influence of the ball.

Solution:

The potentials of the capacitor plates are equal in magnitude and opposite in sign (Fig. 4), that is

When a ball is connected to one of the plates, charges will move to the ball until the potentials of the plate and ball become the same. Ball potential, where is the charge transferred to the ball. Hence,

Answer:

Task 5. A charged ball is suspended on an inextensible insulating thread of length l. The mass of the ball is m, its charge is equal q. At the same height as the suspension point ABOUT on distance 2l a charge is attached to it -q. Find the minimum speed v 0 that the ball must have at the bottom point so that, moving in a circle, it reaches the top point. Neglect the dimensions of the ball.

Solution:

At the top point, the ball is acted upon by gravity and the Coulomb force (there is no elastic force from the thread, since the thread is inextensible (Fig. 5)). The equation of motion of the ball will be written as follows

Let's project this equation onto vertical axis X. The ball moves along a circle of radius l, so along the axis X the normal acceleration of the ball will be directed, which means

(3)

For geometric reasons

After substitution r 2 and in (3) we get

(4)

For the ball to reach the top point, it is necessary that

(5)

The forces acting on the ball are potential, therefore, the conservation law must be satisfied mechanical energy. In the initial position the ball is at the bottom point, in the final position it is at the top. We will count the potential energy of the ball in the Earth's gravity field from the lower position of the ball. Potential energies the electrical interaction of the balls in the initial and final positions are the same. Therefore, the law of conservation of mechanical energy will be written as follows:

(6)

From the joint solution of (4) and (6) taking into account (5) it follows:

Answer:

Task 6. One of the plates of a flat capacitor with an area S suspended on a spring, and the other plate is fixedly fixed (Fig. 6). The distance between the plates at the initial moment of time is equal to d 0. The capacitor was briefly connected to the battery, and it was charged to voltage U. What should the spring stiffness be so that the plates do not touch as a result of their mutual attraction after charging? The displacement of the capacitor plates during charging can be neglected.

Solution:

When charging a capacitor to voltage U charges will appear on its plates +q And -q. The amount of charge will be equal to

Since the distance between the plates of the capacitor is small compared to the size of the plates, the field strength inside the capacitor will be equal to the sum of the field strengths of two infinite plates. The electric field inside the capacitor is uniform. The field strength in this case is related to the potential difference between the capacitor plates by the relation U = E 0 d 0. According to the principle of field superposition, the electric field strength between the plates of the capacitor is equal to the sum of the field strengths created by each plate separately. The charges of the plates are equal in magnitude, therefore, the field strength of one charged plate will be equal to

The upper charged plate is in a uniform electric field of the lower plate, and will be acted upon constant force, directed downwards (Fig. 7), here is the intensity of the electric field created by the lower plate. From the side of the spring, an elastic force will act on the plate, depending on the displacement of the plate and equal in magnitude

Under the action of applied forces, the upper plate will perform harmonic oscillations around a certain equilibrium position. The equilibrium position can be determined from the condition that the resultant of all forces acting on the plate is equal to zero.

Where m- mass of the plate.

The amplitude of oscillations will be equal to the distance l between the equilibrium position of the plate and its initial position. The plates will not touch provided that

The elastic force acting on the plate in the equilibrium position will be equal to

(8)

where is the stretch of the spring when the capacitor is uncharged. It can be determined from the equilibrium condition of the upper plate in the absence of an electric field:

Substituting (8) and (9) into (7), we get

This way the plates will not touch unless

Considering that

Answer:

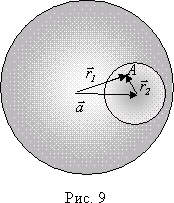
Task 7. Inside a sphere charged uniformly with bulk density, there is a spherical cavity. The center of the cavity is displaced relative to the center of the ball by a distance characterized by a vector (Fig. 8). Find the field strength inside the cavity.

Solution:

If there was no cavity inside the ball, the field strength could be easily calculated using Gauss's theorem. Therefore, you can do this: mentally place a positive and negative density charge inside the cavity and - respectively. This will not change the resulting field, but now the field strength of a ball with a cavity can be calculated as the sum of the field strengths created by solid balls: the large ball is positively charged, and the small one is negatively charged.

Let's calculate the field strength of a uniformly charged ball inside the ball using Gauss's theorem. From symmetry considerations, it is clear that the field lines of a uniformly charged ball will be directed along the radii. Therefore, an arbitrary surface through which the intensity vector flux will be calculated should be chosen in the form of a sphere of radius r (here R- radius of the ball), concentric with the surface of the ball. A charge will enter this sphere

that is, the field strength increases linearly in absolute value with distance from the center of the ball.

Since tension is a vector quantity, it must be written in vector form:

where is the radius vector that determines the position of the point inside the ball relative to its center.

Let us select an arbitrary point inside the cavity A. The position of this point relative to the center of the ball is determined by the radius vector 1, and relative to the center of the cavity - by the radius vector 2 (Fig. 9). Then the field strength at this point, according to the superposition principle, will be equal to

Thus, inside the cavity the electric field will be uniform, the direction of the field lines is parallel to the vector.

Answer:

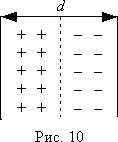
Task 8. A plasma clot has formed in space in the form of an infinite plate of thickness d. The concentration of positively and negatively charged particles is equal n, the charge of each particle is numerically equal q. Then the positively and negatively charged particles moved relative to each other (Fig. 10). Find the field strength at the points of the plane separating them.

Solution:

The resulting accumulation of charges can be divided into very thin layers of thickness , parallel to the separating plane. Each such layer can be considered as infinite plane. Then the field strength created by the resulting accumulation of charges, according to the superposition principle, will be determined as the geometric sum of the electric field strengths created by individual planes. From geometric considerations it is clear that the lines of force of such a plane are perpendicular to it. In the case of a positively charged plane, they leave the plane and end at infinity (Fig. 11), and for negatively charged planes, the field lines begin at infinity and end at the plane (Fig. 12). It is obvious that at the points of the dividing plane the field lines of the negatively and positively charged planes are directed equally.

To calculate the field strength of one plane, we use Gauss's theorem. As an arbitrary surface through which we will consider the flow of the tension vector, we will choose a cylindrical surface, the generatrices of which are perpendicular to the plane, and the bases are located at equal distances from the plane (Fig. 13). Field lines of force do not intersect the plane lateral surface, therefore the flux of the tension vector through it is zero. The lines of force are perpendicular to the bases of the cylindrical surface, so the flux of the tension vector through the cylindrical surface will be equal to

Where E- field strength at the base points of the cylindrical surface, S- base area.

A charge enters the selected surface

Then, according to Gauss's theorem,

Thus, the field of an infinite charged plane is a uniform field.

The field strength at the points of the dividing plane in accordance with the superposition principle will be equal to

Since the lines of force at the points of the dividing plane are directed equally, then

Since the amount is

Answer:

Task 9. The conducting ball is electrified so that the surface charge density is equal to . On distance l from the surface of the ball the field potential is 0. The ball is in the air. What is the capacity of the ball?

Solution:

The capacity of a charged conductor is defined as

Where q- charge of the conductor, - its potential. If the ball has a charge q, the potential on its surface will be equal

Substituting the value into (10), we obtain for the ball capacity

To find the radius of a ball R, we use the expression for the potential of a ball at a distance l from its surface.

here is the charge of the ball. Substituting the value q in (12), we get:

This expression can be rewritten as quadratic equation with the unknown R:

The solution to this equation is:

The negative root has no physical meaning. Substituting the expression for R in (11), we get:

Answer:

Problem 10. Determine the capacitance of the air spherical capacitor. Radii of spheres - R 1 and R 2 .

Solution:

Let us assume that the charge of the inner sphere of radius R 1 is equal to q, and the outer radius R 2 is equal -q. Then the capacitance of the capacitor will be equal to

Option 1

1. Find the potential of an uncharged conducting sphere, outside of which at a distance
l= 30 cm from its center there is a point charge q = 0.50 µC.

2. How does the field strength of a point charge change at a distance A from it if a conductive grounded plate is placed in close proximity to this point?

3. The distance d between the plates of a flat capacitor is 2 mm, the potential difference is U = 1.8 kV. Dielectric – glass (e = 6.0). Determine the dielectric susceptibility c of glass and the surface density σ" of polarization (bound) charges on the glass surface.

4. Two charges are in kerosene () at a distance of 1 cm from each other and interact with a force of 2.7 N. The magnitude of one charge is 3 times greater than the other. Determine the magnitude of each charge.

5. Two parallel metal plates, located in the dielectric with dielectric constant e = 2.2, have a surface charge density of 3 and 2 µC/m 2. Determine the intensity and induction of the electric field between the plates and outside the plates.

CONDUCTORS AND DIELECTRICS IN AN ELECTRIC FIELD

Option 2

1. Two balls, one with a diameter d 1 = 10 cm with a charge q 1 = b 10 -10 C, the other with a diameter d 2 = 30 cm and q 2 = -2 10 -9 C, are connected by a thin wire. What charge will move along it?

2. A point charge q = 5-10 -9 C is located at a distance of 3 cm from a conductive grounded wall. Find the surface charge density induced on the wall at the point closest to the charge.

3. A metal ball of radius R = 5 cm is uniformly surrounded by a layer of porcelain (e = 6.0) with a thickness of d = 2 cm. Determine the surface densities and associated charges, respectively, on the inner and external surfaces dielectric. The charge Q of the ball is 10 nC.

4. Two identical small similarly charged balls are suspended on insulating threads of equal length to one point. When filling environment with kerosene (e = 2.0), the divergence angle did not change. Find the density of the ball material.

5. At some point of an isotropic dielectric with permittivity e, the displacement is equal to . What is the polarization at this point?

CONDUCTORS AND DIELECTRICS IN AN ELECTRIC FIELD

Option 3

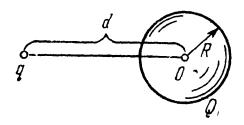
1. A metal ball of radius R has a charge Q. A point charge q is placed at a distance
d from the center of the ball (see figure). Find the potential of ball j.

2. Point charge q = +2-10 -9 C located at a distance
l= 5 cm from a conductive grounded wall. Find the field strength at point A, located at the same distance from the charge q and from the wall l(see picture).

3. An ebonite (e = 2.7) plane-parallel plate is placed in a uniform electric field of intensity E 0 = 2 MV/m. The edges of the plate are perpendicular to the tension lines. Determine the surface density σ" of bound charges on the faces of the plate.

4. Two point charges, being in water () at a distance l from each other, interact with a certain force F. How many times must the distance between them be changed so that they interact with the same force in the air ()?

5. An infinite plane-parallel plate made of a homogeneous and isotropic dielectric with a permittivity e = 2.0 is placed in a uniform electric field with a intensity E 0 = 100 V/m. The plate is located perpendicular to. Determine the field strength E and the electrical displacement D inside the plate.