Charge capacity. Electrical capacity

In an electrostatic field, all points of a conductor have the same potential, which is proportional to the charge of the conductor, i.e. the ratio of charge q to potential φ does not depend on charge q. (Electrostatic is the field surrounding stationary charges). Therefore, it turned out to be possible to introduce the concept of electrical capacitance C of a solitary conductor:

Electrical capacity is a quantity, numerically equal to charge, which must be communicated to the conductor so that its potential changes by one.

Capacitance is determined by the geometric dimensions of the conductor, its shape and properties environment and does not depend on the conductor material.

Units of measurement for quantities included in the definition of capacity:

Capacitance - designation C, unit of measurement - Farad (F, F);

Electric charge - designation q, unit of measurement - coulomb (C, C);

φ - field potential - volts (V, V).

It is possible to create a system of conductors that will have a capacitance much greater than an individual conductor, independent of the surrounding bodies. Such a system is called a capacitor. The simplest capacitor consists of two conductive plates located at a short distance from each other (Fig. 1.9). The electric field of a capacitor is concentrated between the plates of the capacitor, that is, inside it. Capacitor capacity:

C = q / (φ1 - φ2) = q / U

(φ1 - φ2) - potential difference between the plates of the capacitor, i.e. voltage.

The capacitance of a capacitor depends on its size, shape and dielectric constant ε of the dielectric located between the plates.

C = ε∙εo∙S / d, where

S - lining area;

d - distance between plates;

ε is the dielectric constant of the dielectric between the plates;

εo - electrical constant 8.85∙10-12F/m.

If it is necessary to increase the capacitance, the capacitors are connected to each other in parallel.

Fig.1.10. Parallel connection of capacitors.

Ctotal = C1 + C2 + C3

In a parallel connection, all capacitors are under the same voltage, and their total charge is Q. In this case, each capacitor will receive a charge Q1, Q2, Q3, ...

Q = Q1 + Q2 + Q3

Q1 = C1∙U; Q2 = C2∙U; Q3 = C3∙U. Let's substitute into the above equation:

C∙U = C1∙U + C2∙U + C3∙U, whence C = C1 + C2 + C3 (and so on for any number of capacitors).

For serial connection:

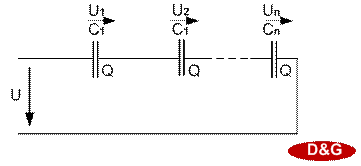
Fig.1.11. Series connection of capacitors.

1/Ctot = 1/C1 + 1/C2 + ∙∙∙∙∙ + 1/ Cn

Derivation of the formula:

Voltage on individual capacitors U1, U2, U3,..., Un. Total voltage of all capacitors:

U = U1 + U2 + ∙∙∙∙∙ + Un,

taking into account that U1 = Q/ C1; U2 = Q/ C2; Un = Q/ Cn, substituting and dividing by Q, we obtain a relationship for calculating the capacitance of a circuit with a series connection of capacitors

Capacitance units:

F - farad. This is a very large value, so smaller values are used:

1 µF = 1 µF = 10-6F (microfarad);

1 nF = 1 nF = 10-9 F (nanofarad);

1 pF = 1pF = 10-12F (picofarad).

When imparting a charge to a conductor, there is always a certain limit beyond which it will not be possible to charge the body. To characterize the body's ability to accumulate electric charge introduce the concept electrical capacitance. The capacitance of an isolated conductor is the ratio of its charge to potential:

In the SI system, capacitance is measured in Farads [F]. 1 Farad is an extremely large capacitance. For comparison, the capacity of only globe significantly less than one farad. The capacitance of a conductor depends neither on its charge nor on the potential of the body. Similarly, density does not depend on either the mass or volume of the body. Capacity depends only on the shape of the body, its size and the properties of its environment.

Electric capacity a system of two conductors is called physical quantity, defined as the charge ratio q one of the conductors to the potential difference Δ φ between them:

The magnitude of the electrical capacitance of conductors depends on the shape and size of the conductors and on the properties of the dielectric separating the conductors. There are conductor configurations in which electric field turns out to be concentrated (localized) only in a certain region of space. Such systems are called capacitors, and the conductors that make up the capacitor are called linings.

The simplest capacitor is a system of two flat conducting plates located parallel to each other at a small distance compared to the size of the plates and separated by a dielectric layer. Such a capacitor is called flat. The electric field of a parallel-plate capacitor is mainly localized between the plates.

Each of the charged plates of a flat capacitor creates an electric field near its surface, the modulus of which is expressed by the relationship already given above. Then the modulus of the final field strength inside the capacitor created by the two plates is equal to:

Outside the capacitor, the electric fields of the two plates are directed in different directions, and therefore the resulting electrostatic field E = 0. Electric capacity of a flat capacitor can be calculated using the formula:

Thus, the electrical capacity of a flat capacitor is directly proportional to the area of the plates (plates) and inversely proportional to the distance between them. If the space between the plates is filled with a dielectric, the capacitance of the capacitor increases by ε once. note that S in this formula there is the area of only one capacitor plate. When they talk about the “plating area” in a problem, they mean exactly this value. You never need to multiply or divide it by 2.

Once again we present the formula for capacitor charge. The charge of a capacitor is understood only as the charge on its positive plate:

The force of attraction between the capacitor plates. The force acting on each plate is determined not by the total field of the capacitor, but by the field created by the opposite plate (the plate does not act on itself). The strength of this field is equal to half the strength of the total field, and the force of interaction between the plates is:

Capacitor energy. It's called energy electric field inside the capacitor. Experience shows that a charged capacitor contains a reserve of energy. The energy of a charged capacitor is equal to the work of external forces that must be expended to charge the capacitor. There are three equivalent forms of writing the formula for the energy of a capacitor (they follow one from the other if we use the relation q = C.U.):

Special attention pay attention to the phrase: “The capacitor is connected to the source.” This means that the voltage across the capacitor does not change. And the phrase “The capacitor was charged and disconnected from the source” means that the charge of the capacitor will not change.

Electric field energy

Electrical energy should be considered as potential energy, stored in a charged capacitor. By modern ideas, Electric Energy of the capacitor is localized in the space between the plates of the capacitor, that is, in the electric field. Therefore it is called electric field energy. The energy of charged bodies is concentrated in space in which there is an electric field, i.e. we can talk about the energy of the electric field. For example, a capacitor's energy is concentrated in the space between its plates. Thus, it makes sense to introduce a new physical characteristics– volumetric energy density of the electric field. Using a flat capacitor as an example, we can obtain the following formula for bulk density energy (or energy per unit volume of electric field):

Capacitor connections

Parallel connection of capacitors– to increase capacity. The capacitors are connected by similarly charged plates, as if increasing the area of the equally charged plates. The voltage on all capacitors is the same, the total charge is equal to the sum of the charges of each capacitor, and the total capacitance is also equal to the sum of the capacitances of all capacitors connected in parallel. Let's write down the formulas for parallel connection capacitors:

At series connection of capacitors the total capacity of a capacitor bank is always less than the capacity of the smallest capacitor included in the battery. A series connection is used to increase the breakdown voltage of the capacitors. Let's write down the formulas for serial connection capacitors. The total capacitance of series-connected capacitors is found from the relationship:

From the law of conservation of charge it follows that the charges on adjacent plates are equal:

The voltage is equal to the sum of the voltages on the individual capacitors.

For two capacitors connected in series, the formula above will give us the following expression for the total capacitance:

For N identical series-connected capacitors:

Conductive sphere

The field strength inside a charged conductor is zero. Otherwise, an electric force would act on the free charges inside the conductor, which would force these charges to move inside the conductor. This movement, in turn, would lead to heating of the charged conductor, which actually does not happen.

The fact that there is no electric field inside the conductor can be understood in another way: if there was one, then the charged particles would again move, and they would move exactly in such a way as to reduce this field to zero with their own field, because in fact, they would not want to move, because every system strives for balance. Sooner or later, all moving charges would stop exactly in that place so that the field inside the conductor would become zero.

On the surface of the conductor, the electric field strength is maximum. The magnitude of the electric field strength of a charged ball outside its boundaries decreases with distance from the conductor and is calculated using a formula similar to the formulas for field strength point charge, in which distances are measured from the center of the ball.

Since the field strength inside a charged conductor is zero, the potential at all points inside and on the surface of the conductor is the same (only in this case the potential difference, and therefore the voltage, is zero). The potential inside a charged ball is equal to the potential on the surface. The potential outside the ball is calculated using a formula similar to the formulas for the potential of a point charge, in which distances are measured from the center of the ball.

Electrical capacity ball radius R:

If the ball is surrounded by a dielectric, then.

Let us consider in more detail the electric field, charges and potential difference (voltage) in a system of two charged bodies separated from each other by insulation.

In this case, we will always assume that the charge of one body is equal and opposite to the charge of another body. This last condition is always fulfilled if the charge is imparted to these two bodies by connecting them to different poles of the same voltage source. In Fig. 4.9, two parallel bodies are depicted as such two bodies. metal plates with a small distance between them.

Rice. 4.9. Two parallel insulated metal plates are connected to a voltage source. These plates form a simple capacitor

Rice. 4.10. Paper capacitor

We know that the greater the charge, the more power the field it creates. But by increasing the field strength, we, of course, increase the voltage: the greater the force, the greater the work, if, of course, the path remains the same.

From what has been said, we can draw the following conclusion: considering any pair of oppositely charged isolated bodies, we will find that at any point in their field the intensity is directly proportional to their charge. But this means that the voltage between them (potential difference) is directly proportional to the charge.

The ratio of charge q to voltage U, which remains unchanged for a given pair of isolated bodies, is called their electrical capacitance:

Accepted letter designation capacity - C. I use it, you can write the following formula:

In the case of parallel plates, the larger the area of the plates and the smaller the distance between the plates, the larger the capacitance.

In fact, by increasing only the area of the plates, we increase the area occupied by the field. If the potential difference, and therefore the field strength, is maintained constant, then the additional area needs to be covered with additional charges.

If you leave the area of the plates and their charge unchanged, then when the plates move closer or further apart, the field strength will not change: between parallel plates, the field strength depends only on their charge.

But at a constant field strength, the potential difference increases with increasing distance between the plates.

If the charge q is expressed in coulombs, and the voltage U is expressed in volts, then; The capacitance value will be expressed in farads (F). A millionth of a farad is called a microfarad (µF).

It is often necessary to use even smaller units of capacitance: one millionth of a microfarad is called a picofarad (pF):

The capacitance of two parallel plates, if the insulation is air, is calculated by the formula

here S is the area of one plate, is the distance between the plates, cm.

With an area S = 50 cm2 and a distance between the plates d = 0.1 cm, the capacitance of the capacitor turns out to be equal to a picofarad, or .

At a voltage of 200 V, the charge on such plates will be equal.

Electrical capacity have almost all elements electrical circuit. Electrical cables have a particularly large capacity.

In electrical engineering, it is often necessary to have a certain capacitance between certain points in a circuit.

For this purpose, artificial devices called capacitors are created. The simplest capacitor of relatively large capacity can be constructed by increasing the area of the plates and reducing the distance between them.

For this purpose, take two thin metal tapes 2 (foil, staniol), place paraffin-impregnated paper 1 between them for insulation and roll them into a bag (Fig. 4.10). The capacity of such capacitors (they are called paper) usually does not exceed millionths of a farad.

Thin mica sheets are also laid between the metal strips as insulation.

So-called electrolytic capacitors have very large capacities; in them, the insulation between the electrolyte and the outer metal shell is the thinnest layer aluminum oxide. A small electrolytic capacitor can be made with a capacity of tens or hundreds of microfarads.

Feature electrolytic capacitor is its suitability only for a certain polarity of the applied voltage - the metal shell must be connected to the negative pole, and the electrode in contact with the electrolyte to the positive pole. Otherwise, the oxide film is decomposed by the passing current and its insulating properties are violated.

In radio engineering, air capacitors with retractable plates are widely used: by turning the handle, they change the mutual overlap of one and the other group of plates, thereby changing that part of the surface of the plates that can be considered to form a capacitor.

The number and variety of types of modern capacitors is extremely large - from the smallest, pressed into plastic, to capacitors about 2 m high, suitable for voltages of 100 thousand V.

By filling the space between the same electrodes with different insulating materials (say, between the plates of a flat-plate capacitor), it is easy to see that the capacitance of the capacitor can change significantly.

Thus, the capacity will increase 7 times if glass is placed between the plates instead of air.

The number showing how many times the capacitance increases when a capacitor is filled with a given insulating medium compared to a vacuum (air) is called the relative dielectric constant of this medium. Dielectric constant is usually denoted Greek letter(epsilon). The dielectric constant of vacuum or electrical constant is equal to

It is easy to understand that the total and absolute dielectric constant of a medium is determined by the product relative permeability to the electrical constant:

When determining the relative dielectric constant, the capacitance value of the capacitor is compared with the capacitance of the same plates with the possible thorough removal of any substance (i.e., in a vacuum).

However, experience shows that filling the space between the plates with air practically does not change the capacitance of the capacitor,

This allows the relative dielectric constant to be determined from a capacitance comparison air condenser with the capacitance of a capacitor filled with the insulation being studied.

Below are the values for several types of insulation:

Electrical capacity of a solitary conductor.

Let's consider a conductor that is distant from other conductors, bodies and charges, and therefore it can be considered as a solitary conductor. From experience it follows that there is a relationship between charge and potential q = Cj.

Value (3.5.2)

called electrical capacitance or simply the capacitance of a solitary conductor. This value is numerically equal to the charge, the communication of which to a conductor increases its potential by one. Capacitance depends on the shape and size of the conductor and does not depend on the material, state of aggregation and on the size of the cavities inside the conductor. Capacitance is also independent of the charge and potential of the conductor. The last statement does not contradict formula (3.5.2). it should be read so that the potential of a conductor is proportional to its charge and inversely proportional to its capacitance. Let's try to find the capacitance of a solitary conductor shaped like a ball with radius R. To do this, we determine the potential of the ball using the formula connecting j and:

. (3.5.3)

If we substitute the obtained result into formula (3.5.2), then for C we obtain:

The unit of capacitance in the SI system is taken to be the capacitance of a conductor whose potential changes by 1V when a charge of 1C is imparted to it. This unit is called the farad (F). Farad is a very large unit. If the earth is considered as a conducting ball with a radius of 6400 km, then its capacitance is approximately 700 × 10 -6 F. Therefore, in practice, we more often encounter capacitances μF = 10 -6 F and nF = 10 -12 F.

Mutual capacitance. Capacitors.

If other conductors are brought closer to a solitary conductor, the capacitance of the first conductor will increase. This is due to the fact that on approaching conductors the field of a given conductor will cause a redistribution of charges. For example, a positively charged conductor on an approaching conductor causes such a redistribution that the induced negative charges are closer to the conductor than the positive ones. Therefore, the potential of the conductor, which is determined by the sum of the potential of its own charges and charges induced on other bodies, will decrease. Consequently, its capacity according to (3.5.2) will increase; thus, it is possible to create a system of conductors that will have a capacity significantly greater than the capacity of a solitary conductor. Of greatest practical interest is a system of conductors located close to each other and charged with charges of equal magnitude but opposite in sign. Such a system is called capacitor, and the conductors are its plates. The capacitance of the capacitor is determined by:

where j 1 - j 2 is the potential difference between the plates, q is the charge located on the positively charged plate of the capacitor. The potential difference is sometimes called voltage and is denoted by the letter U. Therefore, formula (3.5.5) can be written:

According to the shape of the plates, capacitors are flat, cylindrical and spherical. Let's determine the capacitance of a flat capacitor. Let the area of the plate be S and the charge on it be q. The field strength between the plates, as we previously determined

. (3.5.7)

Based on formula (3.4.16), the potential difference between the plates

, (3.5.8)

from here we get for the capacitance of the capacitor:

where d is the distance between the plates; e is the dielectric constant of the medium that fills the gap between the plates. It is easy to obtain the formula for the capacitance of a cylindrical capacitor:

, (3.5.10)

where is the length of the capacitor, R 1 and R 2 are the radii of the inner and outer cylindrical plates. The capacitance of a spherical capacitor is determined by the formula.