Topics of the USE codifier: alternating current, forced electromagnetic oscillations.

Alternating current are forced electromagnetic oscillations caused by electrical circuit source of alternating (most often sinusoidal) voltage.

Alternating current is present everywhere. It flows through the wires of our apartments, in industrial power networks, in high-voltage power lines. And if you need direct current to charge your phone or laptop battery, you use a special adapter that directs alternating current from a wall outlet.

Why is alternating current so widespread? It turns out that it is easy to obtain and ideally suited for transmitting electricity over long distances. We will talk more about this in the leaflet on production, transmission and consumption. electrical energy.

And now we will consider the simplest circuits alternating current. Let's connect to the source AC voltage in turn: resistance resistor, capacitance capacitor and inductor. Having studied the behavior of these elements, we will connect them simultaneously in the next sheet and study the passage of alternating current through an oscillatory circuit with resistance.

The voltage at the source terminals changes according to the law:

(1)

As you can see, the voltage can be positive and negative. What is the meaning of the voltage sign?

It is always assumed that the positive direction of traversal is selected. The voltage is considered positive if electric field charges that form the current has a positive direction. Otherwise, the voltage is considered negative..

The initial voltage phase does not play any role, since we are considering processes that have been established in time. If desired, instead of the sine in expression (1), one could take the cosine - nothing fundamentally changes from this.

The current voltage value at a point in time is called instantaneous voltage value.

Quasi-stationarity condition

In the case of alternating current, there is one subtle point. Let's assume that the circuit consists of several series-connected elements.

If the source voltage changes according to a sinusoidal law, then the current strength does not have time to instantly take on the same value in the entire circuit - it takes some time to transfer interactions between charged particles along the circuit.

Meanwhile, as in the case direct current, we would like to consider the current strength to be the same in all elements of the circuit. Fortunately, in many practically important cases, we do have the right to do so.

Take, for example, an alternating voltage with a frequency of Hz (this is the industrial standard of Russia and many other countries). Voltage fluctuation period: s.

The interaction between charges is transmitted at the speed of light: m/s. For a time equal to the period of oscillations, this interaction will propagate over a distance:

M km.

Therefore, in cases where the length of the circuit is several orders of magnitude less than this distance, we can neglect the propagation time of the interaction and assume that the current strength instantly takes on the same value throughout the entire circuit.

Now consider the general case when the voltage fluctuates with a cyclic frequency. The oscillation period is , and during this time the interaction between the charges is transmitted to a distance . Let be the length of the chain. We can neglect the interaction propagation time if much less than :

(2)

Inequality (2) is called quasi-stationary condition. When this condition is met, we can assume that the current strength in the circuit instantly takes the same value in the entire circuit. This current is called quasi-stationary.

In what follows, we assume that the alternating current changes rather slowly and can be considered quasi-stationary. Therefore, the current strength in all series-connected circuit elements will take same value- at every moment of time. It's called instantaneous current value.

Resistor in AC circuit

The simplest alternating current circuit will be obtained if a conventional resistor is connected to an alternating voltage source (we assume, of course, that the inductance of this resistor is negligible, so that the effect of self-induction can be ignored), also called active resistance(Fig. 1)

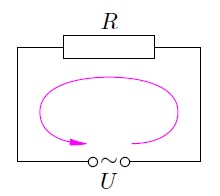
Rice. 1. Resistor in AC circuit

The positive direction of the circuit bypass is selected counterclockwise, as shown in the figure. Recall that the current strength is considered positive if the current flows in a positive direction; otherwise, the current strength is negative.

It turns out that the instantaneous values ​​of current and voltage are related by a formula similar to Ohm's law for direct current:

Thus, the current strength in the resistor also changes according to the sine law:

The current amplitude is equal to the ratio of the voltage amplitude to the resistance:

We see that the current through the resistor and the voltage across it change "synchronously", more precisely, in phase (Fig. 2).

Rice. 2. The current through the resistor is in phase with the voltage

The phase of the current is equal to the phase of the voltage, that is, the phase shift between current and voltage is zero.

Capacitor in AC circuit

Direct current does not flow through the capacitor - for direct current, the capacitor is an open circuit. However, the capacitor is not a hindrance to alternating current! The flow of alternating current through the capacitor is provided by a periodic change in the charge on its plates.

Consider a capacitance connected to a sinusoidal voltage source ( fig. 3). The active resistance of the wires, as always, is considered to be zero. The positive direction of bypassing the circuit is again selected counterclockwise.

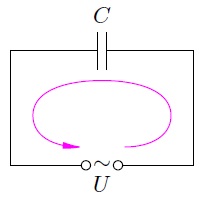
Rice. 3. Capacitor in AC circuit

As before, let's denote by the charge of the capacitor plate to which the positive current flows - in this case it will be the right plate. Then the sign of the value coincides with the sign of the voltage. In addition, as we remember from the previous sheet, with such an agreement on the sign of the charge and the direction of the current, the equality will be satisfied.

The voltage across the capacitor is equal to the source voltage:

Differentiating this equality with respect to time, we find the current through the capacitor:

(3)

Graphs of current and voltage are presented in fig. 4 . We see that the current each time reaches a maximum a quarter of a period earlier than the voltage. This means that the phase of the current is greater than the phase of the voltage (the current leads the voltage in phase by ).

Rice. 4. The current through the capacitor leads the voltage in phase by

You can also find the phase shift between current and voltage using the reduction formula:

Using it, we get from (3) :

And now we clearly see that the phase of the current is greater than the phase of the voltage by .

For the current amplitude we have:

Thus, the amplitude of the current strength is related to the amplitude of the voltage by a relationship similar to Ohm's law:

The value is called capacitive resistance capacitor. The larger the capacitance of the capacitor, the smaller the amplitude of the current flowing through it, and vice versa.

Capacitive resistance is inversely proportional to the cyclic frequency of voltage (current) oscillations and the capacitance of the capacitor. Let's try to understand the physical reason for this dependence.

1. The higher the oscillation frequency (with a fixed capacitance), the faster the charge passes through the circuit; the greater the amplitude of the current and the lower the capacitance. When capacitive resistance tends to zero: . This means that for a high frequency current, the capacitor is actually short circuit chains.

On the contrary, as the frequency decreases, the capacitance increases, and at , we have . This is not surprising: the case corresponds to direct current, and the capacitor for direct current is an infinite resistance (open circuit).

2. The larger the capacitance of the capacitor (at fixed frequency), the greater the charge passes through the circuit in the same time (for the same quarter of the period); the greater the amplitude of the current and the lower the capacitance.

We emphasize that, in contrast to the situation with a resistor, instant the values ​​of current and voltage at the same instants of time will no longer satisfy a relationship similar to Ohm's law. The reason is the phase shift: the voltage changes according to the sine law, and the current strength - according to the cosine law; these functions are not proportional to each other. Ohm's law is related only amplitude current and voltage values.

Coil in AC circuit

Now let's connect an inductor to our AC voltage source ( fig. 5). The active resistance of the coil is considered to be zero.

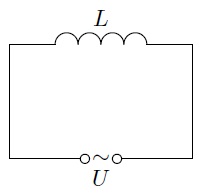
Rice. 5. Coil in AC circuit

It would seem that at zero active (or, as they say, ohmic) resistance, an infinite current should flow through the coil. However, the coil offers a different kind of resistance to the alternating current.
The magnetic field of the current, which changes with time, generates a vortex electric field in the coil, which, it turns out, exactly balances the Coulomb field of moving charges:

(4)

The work of the Coulomb field to move a unit positive charge along the external circuit in a positive direction is just voltage. The analogous work of the vortex field is the induction emf.

Therefore, from (4) we get:

(5)

Equality (5) can also be explained from the energy point of view. Let's assume it doesn't work. Then, when the charge moves along the circuit, non-zero work is performed, which must be converted into heat. But thermal power is equal to zero at zero ohmic resistance of the circuit. The resulting contradiction shows that equality (5) must hold.

Remembering Faraday's law, we rewrite the relation (5):

(6)

It remains to find out which function, which changes according to the harmonic law, must be differentiated in order to obtain the right side of the expression (6) . It's easy to figure this out (differentiate and test!):

(7)

We have obtained an expression for the current through the coil. Graphs of current and voltage are presented in fig. 6.

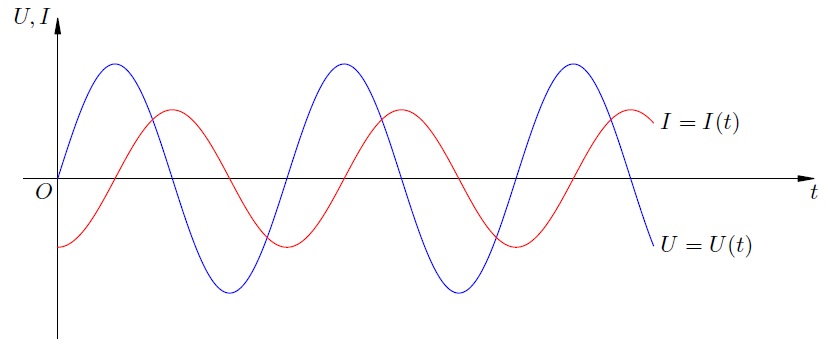
Rice. 6. The current through the coil is out of phase with the voltage across

As you can see, the current strength reaches each of its maximums a quarter of a period later than the voltage. This means that the current is out of phase with the voltage by .

You can also determine the phase shift using the reduction formula:

We get:

We can directly see that the current phase is less than the voltage phase by .

The amplitude of the current through the coil is:

This can be written in a form similar to Ohm's law:

Let the current source create an alternating harmonic voltage (figure)

U(t) = U o sinωt. (1)

According to Ohm's law, the current strength in a circuit section containing only a resistor with resistance R, connected to this source, also changes with time according to a sinusoidal law:

I(t) = U(t)/R = (U o /R)sinωt = I o sinωt,

Where I o \u003d U o /R? amplitude value of the current strength in the circuit.
As you can see, the current strength in such a circuit also changes with time according to a sinusoidal law.
Quantities U o And I o \u003d U o /R are called amplitude values ​​of voltage and current. Voltage values U(t) and current I(t) that depend on time are called instantaneous.
Knowing instantaneous values U(t) And I(t), you can calculate the instantaneous power P(t) = U(t)I(t), which, unlike DC circuits, changes over time.
Taking into account the dependence of the current strength on time in the circuit, we rewrite the expression for the instantaneous thermal power on the resistor in the form

P(t) = U(t)I(t) = I 2 (t)R = I o 2 Rsin 2 ωt.

Since the instantaneous power varies with time, it is extremely inconvenient in practice to use this value as a characteristic of long-term processes.
Let's rewrite the formula for power in a different way:

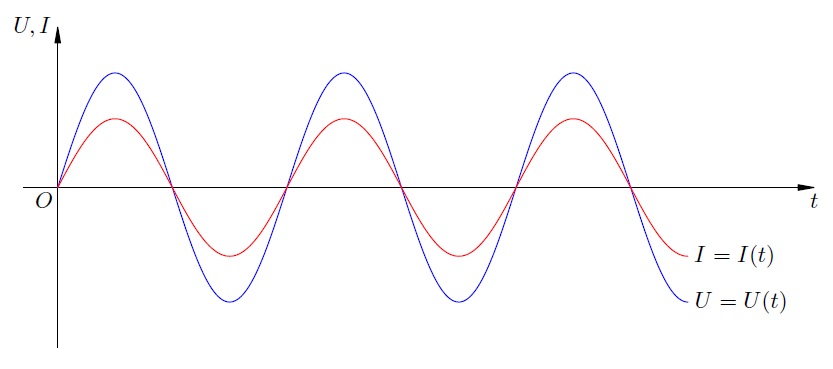
P \u003d UI \u003d U o I o sin 2 ωt \u003d (1/2) U o I o (1? cos2ωt) \u003d U o I o /2? (U o I o /2)cos2ωt.

The first term does not depend on time. The second term? variable component? the cosine function of the double angle and its average value over the oscillation period is zero (see figure).
Therefore, the average value of the AC power electric current over a long period of time can be found by the formula

P cp \u003d U o I o /2 \u003d I o 2 /R.

This expression allows you to enter the effective (effective) values ​​​​of current and voltage, which are used as the main characteristics of alternating current.
current The (effective) value of the alternating current strength is the strength of such a direct current, which, passing through the circuit, releases the same amount of heat per unit time as the given alternating current.
Since for direct current

P post \u003d I 2 R,

Then, taking into account the previously obtained expression for the average value of the AC power, the effective value of the current

I d \u003d I o /? 2.

Similarly, you can enter the effective value for voltage

U d \u003d U o /? 2.

Thus, the expressions for calculating the power consumed in DC circuits remain valid for alternating current, if we use the effective values ​​​​of current and voltage in them:

P \u003d U d I d \u003d I d 2 R \u003d U d 2 / R, I d \u003d U d / R.

41.1. Voltage and resistance triangles.

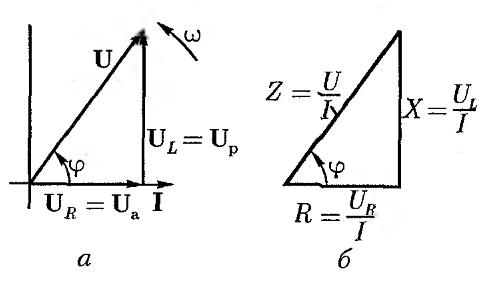
Amplitudes of the components of the total voltage:

Valid values:

Total voltage vector:

In order to find the value of the vector U, we construct vector diagram(Fig. a). We take the current vector I as the initial vector of the diagram. The direction of this vector coincides with the positive direction of the axis from which the phase angles are measured.

The direction vector coincides with the current vector I, and the vector is directed perpendicular to the vector I with a positive angle.

It can be seen from the diagram that the total voltage vector U leads the current vector I by an angle >0, but< , а по величине равен гипотенузе right triangle, the legs of which are the vectors of voltage drops in the active and inductive resistances and : = Ucos

The projection of the voltage vector U onto the direction of the current vector is called the active component of the voltage vector and is denoted by Ua. Ua =

The projection of the voltage vector U onto the direction perpendicular to the current vector is called the reactive component of the voltage vector and is denoted by Up. Up =

The sides of the voltage triangle, expressed in units of voltage, are divided by the current I. We get a similar resistance triangle (Fig. b), the legs of which are active and inductive resistances, and the hypotenuse is the value.

The ratio of the effective voltage to operating current of this circuit is called the impedance of the circuit. The sides of the resistance triangle cannot be considered vectors, since resistances are not functions of time.

From the resistance triangle follows:

41.2. Impedance.

Impedance (Z) is the vector sum of all resistances: active, capacitive and inductive.

circuit impedance.

41.3. Phase angle between voltage and current.

The complex resistance argument j is the difference between the initial phases of voltage and current, but it can also be determined from the real and imaginary components of the complex resistance as j = arctg( X/R). Hence, phase shift between voltage and current is determined only by the load parameters and does not depend on the current and voltage parameters in the circuit . From expression 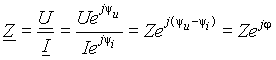follows that positive values j correspond to the current lagging in phase, and negative ones to lead.

41.4. Ohm's law for effective and amplitude values ​​of current and voltage.

On the active element r an irreversible electrical transformation takes place.

energy in thermal energy. Instantaneous currents i and stress u connected

Ohm's law:

If the current changes sinusoidally then voltage:

On the other hand, the instantaneous voltage value:

From here, Ohm's law for the amplitude values ​​is obtained: , and Ohm's law for effective values:

42. Energy process. Instantaneous, active, reactive and apparent power. Power Triangle. Power factor .

instantaneous power is the product of the instantaneous values ​​of voltage and current in any section of the electrical circuit
By definition, electrical voltage is the ratio of work electric field committed when transferring the trial electric charge from point A to point B, to the value of the test charge. That is, we can say that the electric voltage is equal to the work of transferring a unit charge from point A to point B. In other words, when a unit charge moves along a section of an electric circuit, it will do work numerically equal to electrical voltage acting on the section of the chain. Multiplying the work by the number of unit charges, we thus get the work that these charges do when moving from the beginning of the chain section to its end. Power, by definition, is work per unit of time. Let's introduce the notation: U- voltage in the section A-B (we take it constant over the interval Δ t), Q- the number of charges passing from A to B in time Δ t. A- work done by charge Q when moving along section A-B, P- power. Writing down the above reasoning, we get:

For all charges:

Assuming time to be infinitely small, we can assume that the values ​​of voltage and current during this time will also change infinitesimally. As a result, we get the following definition instant electrical power:

instantaneous electrical power p(t), which stands out in the section of the electric circuit, is the product of the instantaneous voltage values u(t) and current i(t) in this section:

Active power
Measured in W [W] Watt.
Average for the period T meaning instant power is called active power. In single-phase circuits sinusoidal current Where U And I- rms values ​​of voltage and current, φ - phase angle between them. For non-sinusoidal current circuits, the electrical power is equal to the sum of the corresponding average powers of the individual harmonics. Active power characterizes the rate of irreversible transformation of electrical energy into other types of energy (thermal and electromagnetic). Active power can also be expressed in terms of current, voltage and active component of the circuit resistance. r or its conductivity g according to the formula In any electrical circuit, both sinusoidal and non-sinusoidal current active power of the entire circuit is equal to the sum of active powers separate parts chains, for three-phase circuits electrical power is defined as the sum of the powers of the individual phases. With full power S active is related by the ratio

Reactive power

Unit of measurement - volt-ampere reactive (var, var)

Reactive power is a value that characterizes the loads created in electrical devices fluctuations in the energy of the electromagnetic field in the sinusoidal alternating current circuit, is equal to the product of the root-mean-square voltage values U and current I, multiplied by the sine of the phase shift angle φ between them: (if the current lags behind the voltage, the phase shift is considered positive, if it leads, it is negative). Reactive power is related to apparent power S and active power R ratio: .

The physical meaning of reactive power is the energy pumped from the source to the reactive elements of the receiver (inductances, capacitors, motor windings), and then returned by these elements back to the source during one oscillation period, related to this period.

It should be noted that the value of sin φ for values ​​of φ from 0 to plus 90° is a positive value. The sin φ value for φ values ​​from 0 to −90° is a negative value. According to the formula Q = UI sin φ, reactive power can be either positive (if the load is active-inductive) or negative (if the load is active-capacitive). This circumstance emphasizes the fact that reactive power is not involved in the work of electric current. When a device has positive reactive power, it is customary to say that it consumes it, and when it has negative reactive power, it produces it, but this is a pure convention due to the fact that most power-consuming devices (for example, asynchronous motors), as well as a purely active load connected through a transformer, are active-inductive.

Synchronous generators installed on power stations, can both produce and consume reactive power, depending on the magnitude of the excitation current flowing in the generator rotor winding. Due to this feature of synchronous electrical machines regulation of the set voltage level of the network is carried out. To eliminate overloads and improve power factor electrical installations reactive power is compensated.

The use of modern electrical measuring transducers on microprocessor technology allows a more accurate assessment of the amount of energy returned from the inductive and capacitive load to the AC voltage source.

Reactive power transducers using the formula Q = UI sin φ, are simpler and much cheaper than measuring transducers based on microprocessor technology.

Full power

The unit of apparent electrical power is volt-ampere (V A, V A)

Apparent power - a value equal to the product of the effective values ​​\u200b\u200bof periodic electric current I in circuit and voltage U on her clamps: S = U I; is related to active and reactive power by the ratio: Where R- active power, Q- reactive power (with inductive load Q> 0, and with capacitive Q < 0).

The vector dependence between apparent, active and reactive power is expressed by the formula:

Apparent power is of practical importance, as a value that describes the loads actually imposed by the consumer on the elements of the supply network (wires, cables, switchboards, transformers, power lines), since these loads depend on the consumed current, and not on the energy actually used by the consumer. That is why the power rating of transformers and switchboards is measured in Volt-Amps and not in Watts.

We have seen that the instantaneous value of the alternating current changes all the time, fluctuating between zero and a maximum value. Nevertheless, we characterize the strength of the alternating current, as well as the strength of the direct current, certain number ampere. We say, for example, that in one bulb there is a current equal to 0.25 A, and in another, more powerful, a current equal to 0.5 A, etc. What is the meaning of this statement? What does the expression "AC power" mean?

It would be possible to characterize the strength of an alternating current by its amplitude. In principle, this is quite possible, but in practice it is very inconvenient, because it is difficult to build instruments that directly measure the amplitude of the alternating current. It is more convenient to use some property of it that does not depend on the direction of the current to characterize the alternating current. Such a property is, for example, the ability of current to heat the conductor through which it passes. This heating does not depend on the direction of the current, it is produced by alternating current when passing both in one direction and in the opposite direction.

Imagine an alternating current passing through some conductor with resistance. Within a second, the current releases a certain amount of heat in the conductor, say. Let us pass a direct current through the same conductor, choosing its strength so that it releases the same amount of heat in the conductor every second. In their action, both currents are equal; therefore, the direct current strength characterizes the effective value of the alternating current, which is denoted by.

The strength of a direct current that releases the same amount of heat in a conductor as a given alternating current is called the effective value of the alternating current.

It follows from the foregoing that, by replacing the direct current in formula (56.1) with the effective value of the alternating current, we can calculate the amount of heat generated by the alternating current in the conductor:

We emphasize again that in this formula it denotes the effective value of the alternating current. When we say that an alternating current is, say, 2 A, we want to say that the thermal effect of this current is the same as the thermal effect of a direct current of 2 A.

In the case of a sinusoidal current, the effective value of the current is quite simply related to the amplitude of this current. The corresponding calculation gives that

. (154.2)

Thus, by measuring the effective value of the sinusoidal current, it is possible to calculate its amplitude using the formula (154.2).

154.1. In a conductor with a resistance of 50 ohms, through which an alternating current flowed, an amount of heat equal to 6 kJ was released in 2.5 hours. What is the effective value of the current and what is the amplitude of the current?

154.2. In a conductor with a resistance of 10 ohms, an alternating current releases an amount of heat per second equal to 1 kJ. What is the effective value of the current?

154.3. The amplitude of the sinusoidal alternating current is 5 A. What is its effective value?

154.4. The effective value of the alternating sinusoidal current is 14.2 A. What is the amplitude of this current?

Let's move on to a more detailed consideration of the processes that occur in a circuit connected to an alternating voltage source.

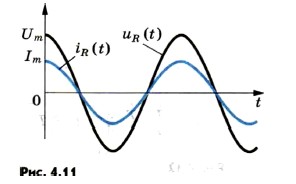
Let the circuit consist of connecting wires and a load with low inductance and high resistance R (Fig. 4.10). This quantity, which we have so far called electrical resistance or simply resistance, now we will call active resistance.

The resistance R is called active, because in the presence of a load with this resistance, the circuit absorbs the energy coming from the generator. This energy is converted into the internal energy of the conductors - they heat up. We assume that the voltage at the circuit terminals changes according to the harmonic law:

u = U m cos ωt.

As in the case of direct current, the instantaneous value of the current is directly proportional to the instantaneous value of the voltage. Therefore, to find the instantaneous value of the current strength, Ohm's law can be applied:

In a conductor with active resistance, current fluctuations coincide in phase with voltage fluctuations (Fig. 4.11), and the amplitude of the current strength is determined by the equality

Power in a circuit with a resistor. In an alternating current circuit of industrial frequency (v \u003d 50 Hz), the current and voltage change relatively quickly. Therefore, when current passes through a conductor, for example, through a thread light bulb, the amount of released energy will also change rapidly with time. But we do not notice these rapid changes.

As a rule, we need to know average power current in a circuit section over a long period of time, including many periods. To do this, it is enough to find the average power for one period. The average AC power for a period is understood as the ratio of the total energy entering the circuit for a period to the period.

The power in the DC circuit in the section with resistance R is determined by the formula

Р = I 2 R. (4.18)

For a very short time interval, the alternating current can be considered almost constant. Therefore, the instantaneous power in the AC circuit in the section having active resistance R, is determined by the formula

Р = i 2 R. (4.19)

Let's find the average power value for the period. To do this, we first transform formula (4.19), substituting expression (4.16) for the current strength into it and using the relation known from mathematics

The plot of instantaneous power versus time is shown in Figure 4.12, a. According to the graph (Fig. 4.12, b), during one eighth of the period, when cos 2ωt > 0, the power at any time is greater than But during the next eighth of the period, when cos 2ωt< 0, мощность в любой момент времени меньше, чем Среднее за период значение cos 2ωt равно нулю, а значит равно нулю второе слагаемое в уравнении (4.20).

From formula (4.21) it can be seen that the value is the average value of the squared current strength over the period:

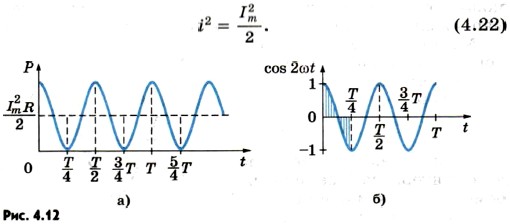
A value equal to square root from the average value of the square of the current, is called effective value of alternating current. The effective value of the alternating current is denoted by I:

It is equal to the strength of such direct current, at which the same amount of heat is released in the conductor as with alternating current for the same time.

The effective value of the alternating voltage is determined similarly to the effective value of the current:

Replacing the amplitude values ​​of the current and voltage in formula (4.17) with their effective values, we obtain

This is Ohm's law for a section of an AC circuit with a resistor.

As with mechanical vibrations, in the case of electrical vibrations, we are usually not interested in the values ​​​​of current, voltage, and other quantities at any given time. Important General characteristics oscillations, such as amplitude, period, frequency, effective values ​​of current and voltage, average power. It is the effective values ​​​​of current and voltage that are recorded by ammeters and voltmeters of alternating current.

In addition, the effective values ​​are more convenient than the instantaneous values ​​also because they directly determine the average value of the AC power P:

p = I 2 R = UI.

Current fluctuations in a circuit with a resistor are in phase with voltage fluctuations, and the power is determined by effective values current and voltage.

Questions for the paragraph

1. What is the voltage amplitude in AC lighting networks rated for 220 V?

2. What is called the effective values ​​​​of current and voltage?