एक आयताकार द्वारा निर्मित चुंबकीय क्षेत्र का प्रेरण ज्ञात कीजिए

जब निर्वात में स्थित एक बंद लूप से प्रत्यक्ष धारा गुजरती है, तो लूप से दूरी पर स्थित एक बिंदु के लिए, चुंबकीय प्रेरण का रूप होगा:

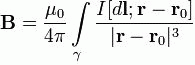
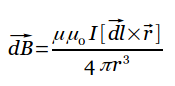
यदि एक चुंबकीय सुई को धारा ले जाने वाले सीधे कंडक्टर के करीब लाया जाता है, तो यह कंडक्टर की धुरी और सुई के घूर्णन के केंद्र से गुजरने वाले विमान के लंबवत हो जाएगी (चित्र 67)।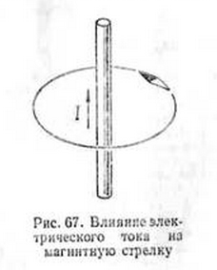

यह इंगित करता है कि सुई विशेष बलों के अधीन है जिन्हें चुंबकीय बल कहा जाता है। दूसरे शब्दों में, यदि कोई कंडक्टर गुजरता है बिजली, तो कंडक्टर के चारों ओर एक चुंबकीय क्षेत्र दिखाई देता है।

एक चुंबकीय क्षेत्र को वर्तमान-वाहक कंडक्टरों के आसपास के स्थान की एक विशेष स्थिति के रूप में माना जा सकता है। चुंबकीय क्षेत्र की गणना करते समय, एक मात्रा कहा जाता है तनाव चुंबकीय क्षेत्र (एच दर्शाया गया है)। चुंबकीय प्रेरण बी और चुंबकीय क्षेत्र की ताकत एच संबंध से संबंधित हैं:

चुंबकीय क्षेत्र की ताकत के माप की इकाई एम्पीयर प्रति मीटर (ए/एम) है।

एक सजातीय माध्यम में चुंबकीय क्षेत्र की ताकत, साथ ही चुंबकीय प्रेरण, धारा के परिमाण, उन कंडक्टरों की संख्या और आकार पर निर्भर करती है जिनसे होकर धारा गुजरती है। लेकिन चुंबकीय प्रेरण के विपरीत, चुंबकीय क्षेत्र की ताकत माध्यम के चुंबकीय गुणों के प्रभाव को ध्यान में नहीं रखती है।

34. धारा के साथ एक गोलाकार कुंडल की धुरी पर चुंबकीय क्षेत्र के बीएस कानून का उपयोग करके गणना। डायपोल के विद्युत क्षेत्र के साथ सादृश्य।

चुंबकीय क्षेत्र की ताकत का अनुपात है यांत्रिक बल, एक परीक्षण चुंबक के सकारात्मक ध्रुव पर कार्य करते हुए, क्षेत्र में किसी दिए गए बिंदु पर इकाई द्रव्यमान के एक परीक्षण चुंबक के सकारात्मक ध्रुव पर कार्य करने वाले उसके चुंबकीय द्रव्यमान या यांत्रिक बल के मूल्य पर। तीव्रता को एक वेक्टर द्वारा दर्शाया जाता है एच, यांत्रिक बल वेक्टर की दिशा वाले एफ: .वर्तमान तत्व- एक रैखिक कंडक्टर और इस कंडक्टर के एक अनंत खंड के साथ चालन धारा के उत्पाद के बराबर एक वेक्टर मात्रा। . टिप्पणी. वर्तमान तत्व की दिशा इस खंड की दिशा से मेल खाती है। बायोट-सावर्ट-लाप्लास कानून - भौतिक नियमप्रत्यक्ष विद्युत धारा द्वारा उत्पन्न चुंबकीय क्षेत्र के प्रेरण वेक्टर को निर्धारित करने के लिए।

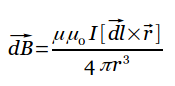
धारा प्रवाहित करने वाला वृत्ताकार चालक।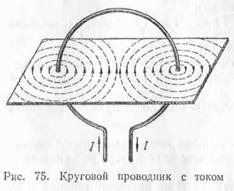

आइए एक कुंडल के रूप में एक वृत्त में मुड़े हुए कंडक्टर को लें और इसके माध्यम से करंट प्रवाहित करें (चित्र 75)। चित्र से यह देखा जा सकता है कि चुंबकीय रेखाएँ धारावाही चालक के चारों ओर बंद हैं और वृत्तों के आकार की हैं। चुंबकीय रेखाएं एक ओर से वृत्ताकार चालक के तल में प्रवेश करती हैं, दूसरी ओर से बाहर निकलती हैं। वृत्ताकार धारा क्षेत्र की दिशा "जिम्लेट नियम" का उपयोग करके निर्धारित की जा सकती है। गिम्लेट को वृत्ताकार धारा के अक्ष के अनुदिश लंबवत स्थित होना चाहिए इसका विमान. यदि आप अब सर्किट में करंट की दिशा में गिम्लेट के हैंडल को घुमाते हैं, तो गिम्लेट की ट्रांसलेशनल गति चुंबकीय क्षेत्र की दिशा दिखाएगी। धारा के साथ कुंडल के केंद्र में चुंबकीय क्षेत्र की ताकत सूत्र द्वारा निर्धारित की जाती है:

35. चुंबकीय प्रेरण वेक्टर का प्रवाह (चुंबकीय प्रवाह) और इसका ज्यामितीय अर्थ। चुंबकीय क्षेत्र के लिए ओजी प्रमेय।

क्षेत्र dS के माध्यम से चुंबकीय प्रेरण वेक्टर (चुंबकीय प्रवाह) के प्रवाह को अदिश कहा जाता है भौतिक मात्रा, बराबर जहां Bn=B cos a, साइट dS के सामान्य की दिशा पर वेक्टर B का प्रक्षेपण है (a वेक्टर n और B के बीच का कोण है), dS=dSn एक वेक्टर है जिसका मापांक dS के बराबर है, और इसकी दिशा साइट पर सामान्य n की दिशा से मेल खाता है। वेक्टर बी का प्रवाह कॉस ए के संकेत के आधार पर या तो सकारात्मक या नकारात्मक हो सकता है (सामान्य एन की सकारात्मक दिशा की पसंद से निर्धारित होता है)। वेक्टर बी का प्रवाह उस सर्किट से जुड़ा होता है जिसके माध्यम से करंट प्रवाहित होता है। इस मामले में, समोच्च के लिए सामान्य की सकारात्मक दिशा पहले से ही हमारे द्वारा निर्धारित की गई है: यह सही पेंच के नियम द्वारा वर्तमान से जुड़ा हुआ है। इस प्रकार, सर्किट द्वारा स्वयं द्वारा सीमित सतह के माध्यम से बनाया गया चुंबकीय प्रवाह हमेशा सकारात्मक होता है। एक मनमानी सतह एस के माध्यम से चुंबकीय प्रेरण वेक्टर एफबी का प्रवाह के लिए एकसमान क्षेत्रऔर वेक्टर बी के लंबवत स्थित एक सपाट सतह, बीएन = बी = स्थिरांक और इस सूत्र से चुंबकीय प्रवाह वेबर (डब्ल्यूबी) की इकाई निर्धारित की जाती है: 1 डब्ल्यूबी - 1 एम 2 के क्षेत्र के साथ एक सपाट सतह से गुजरने वाला चुंबकीय प्रवाह स्थित है एक समान चुंबकीय क्षेत्र के लंबवत, जिसका प्रेरण 1 T (1 Wb=1 T×m2) के बराबर है। फ़ील्ड बी के लिए गॉस का प्रमेय: किसी भी बंद सतह के माध्यम से चुंबकीय प्रेरण वेक्टर का प्रवाह शून्य है: यह प्रमेय इस तथ्य को दर्शाता है कि कोई नहीं है चुंबकीय आवेश, जिसके परिणामस्वरूप चुंबकीय प्रेरण की रेखाओं का न तो आरंभ होता है और न ही अंत और वे बंद हो जाती हैं। तो, भंवर और संभावित क्षेत्रों में एक बंद सतह के माध्यम से वैक्टर बी और ई के प्रवाह के लिए, परिणाम अलग-अलग हैं। उदाहरण के तौर पर, आइए सोलनॉइड के माध्यम से वेक्टर बी के प्रवाह की गणना करें। चुंबकीय पारगम्यता एम के साथ एक कोर के साथ एक परिनालिका के अंदर एक समान क्षेत्र का चुंबकीय प्रेरण, क्षेत्र एस के साथ परिनालिका के एक मोड़ के माध्यम से चुंबकीय प्रवाह के बराबर है और परिनालिका के सभी घुमावों से जुड़ा कुल चुंबकीय प्रवाह के बराबर है और फ्लक्स लिंकेज कहा जाता है, . धारा प्रवाहित सर्किट का चुंबकीय क्षण। चुंबकीय क्षेत्र में विद्युत धारा वाला सर्किट। अनुभव से पता चलता है कि विद्युत धाराएँ एक दूसरे के साथ परस्पर क्रिया करती हैं, उदाहरण के लिए, मैं धाराओं को आकर्षित करता हूँ, और धाराएँ प्रतिकर्षित करती हैं। धाराओं की परस्पर क्रिया चुंबकीय नामक क्षेत्र के माध्यम से होती है। नतीजतन, गतिमान आवेश (धाराएं) अपने आस-पास के स्थान के गुणों को बदल देते हैं - वे इसमें एक चुंबकीय क्षेत्र बनाते हैं। यह क्षेत्र इस तथ्य में प्रकट होता है कि बल इसमें चलने वाले आवेशों (धाराओं) पर कार्य करते हैं। अनुसंधान के समान विद्युत क्षेत्रहमने एक परीक्षण चार्ज का उपयोग किया; चुंबकीय क्षेत्र का अध्ययन करने के लिए, हम बहुत छोटे आयामों के एक फ्लैट बंद सर्किट में प्रसारित एक परीक्षण वर्तमान का उपयोग करेंगे। ऐसे सर्किट को हम ट्रायल सर्किट कहेंगे। अंतरिक्ष में इसका अभिविन्यास समोच्च के लिए सामान्य एन (वेक्टर) की दिशा की विशेषता है, जिसे दाएं गिम्लेट के नियम के अनुसार बहाल किया जाता है: हम सर्किट में वर्तमान की दिशा में दाएं गिम्लेट के हैंडल को घुमाते हैं, फिर इसके ट्रांसलेशनल मूवमेंट की दिशा सामान्य n(वेक्टर) की दिशा देगी (चित्र 1 देखें)। एक परीक्षण सर्किट को चुंबकीय क्षेत्र में रखकर, हम पाते हैं कि क्षेत्र सर्किट को एक निश्चित दिशा में (सामान्य) घुमाता है। 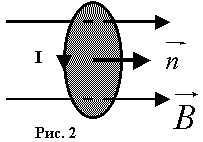सर्किट पर कार्य करने वाला टॉर्क किसी दिए गए बिंदु पर चुंबकीय क्षेत्र के गुणों और सर्किट के गुणों दोनों पर निर्भर करता है। यह पता चला है कि अधिकतम टोक़ मान आईएस के समानुपाती है, अर्थात। Mmax ~ IS, जहां I सर्किट में करंट है, S करंट वाले सर्किट का क्षेत्र है (चित्र 1)। वेक्टर मात्रा (1) को सर्किट का चुंबकीय क्षण कहा जाता है, जिसे SI में A×m2 में मापा जाता है। चुंबकीय क्षेत्र में किसी दिए गए बिंदु पर रखे गए अलग-अलग पीएम वाले परीक्षण सर्किट अलग-अलग अधिकतम टॉर्क एम के अधीन होंगे, लेकिन सभी सर्किटों के लिए अनुपात एममैक्स/पीएम समान होगा; यह चुंबकीय क्षेत्र की बल विशेषता होगी, जो है चुंबकीय प्रेरण कहा जाता है बी = एममैक्स /पीएम चुंबकीय प्रेरण एक वेक्टर है, जिसकी दिशा वर्तमान के साथ एक सर्किट के सामान्य की दिशा से मेल खाती है, जो बाहरी चुंबकीय क्षेत्र में स्वतंत्र रूप से स्थापित है (चित्र 2 देखें)। वेक्टर बी का क्षेत्र बल की रेखाओं का उपयोग करके दर्शाया जा सकता है, (चित्र 2 देखें), साथ ही वेक्टर क्षेत्र इस प्रकार बी ई का एक एनालॉग है। एसआई में चुंबकीय प्रेरण टेस्ला में मापा जाता है: 1 टी = 1 एनएम / 1 ए × एम 2। टेस्ला एक समान क्षेत्र के चुंबकीय प्रेरण के बराबर है, जिसमें 1 एनएम का अधिकतम टॉर्क एक फ्लैट सर्किट पर धारा के साथ कार्य करता है जिसमें 1 ए एम 2 का चुंबकीय क्षण होता है। प्रेरण के साथ चुंबकीय क्षेत्र में रखे गए एक धारा-वाहक सर्किट पर एक टोक़ द्वारा कार्य किया जाता है जिसका परिमाण M = है। एक चुंबकीय क्षेत्र में एक कंडक्टर और करंट ले जाने वाले सर्किट को घुमाने पर काम करें। चलते समय किसी चालक द्वारा धारा पर किया गया कार्य संख्यात्मक रूप से इस चालक द्वारा पार किए गए धारा और चुंबकीय प्रवाह के उत्पाद के बराबर होता है। आइए स्थिर तारों और उनके साथ सरकने वाले l लंबाई के एक जंगम जम्पर द्वारा निर्मित एक विद्युत धारा-वाहक सर्किट पर विचार करें (चित्र 2.17)। यह सर्किट एक बाहरी समान चुंबकीय क्षेत्र बी में स्थित है, जो सर्किट के तल के लंबवत है। चित्र में दर्शाई गई धारा I की दिशा के साथ, वेक्टर B, n के साथ सह-दिशात्मक है। 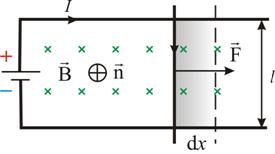लंबाई l का एक वर्तमान तत्व I (एक गतिमान तार) पर दाईं ओर निर्देशित एक एम्पीयर बल द्वारा कार्य किया जाता है: कंडक्टर l को कुछ दूरी तक अपने समानांतर चलने दें। इस मामले में, काम पूरा हो जाएगा: तो: यदि किसी भी आकार का कंडक्टर चुंबकीय प्रेरण वेक्टर की रेखाओं पर किसी भी कोण पर चलता है तो सूत्र वैध रहता है। किसी बंद लूप को चुंबकीय क्षेत्र में धारा के साथ घुमाने पर किया गया कार्य धारा के परिमाण और इस लूप से जुड़े चुंबकीय प्रवाह में परिवर्तन के उत्पाद के बराबर होता है। 1-2-3-4-1 धारा वाले एक आयताकार परिपथ पर विचार करें 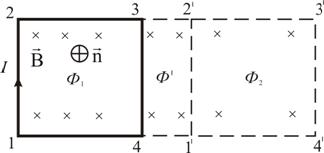(चित्र 2.18)। चुंबकीय क्षेत्र समोच्च तल के लंबवत हमसे दूर निर्देशित होता है। इसलिए, सर्किट में प्रवेश करने वाला चुंबकीय प्रवाह सामान्य n के साथ सर्किट की ओर निर्देशित होता है। चावल। 2.18 आइए इस सर्किट को अपने समानांतर एक नई स्थिति 1"-2"-3"-4"-1" पर ले जाएं। सामान्य स्थिति में चुंबकीय क्षेत्र गैर-समान हो सकता है और नया सर्किट एक चुंबकीय प्रवाह द्वारा प्रवेश करेगा . क्षेत्र 4-3-2"-1"-4, पुराने और नए सर्किट के बीच स्थित, प्रवाह द्वारा प्रवेश किया जाता है। पूरा कामचुंबकीय क्षेत्र में सर्किट को घुमाने से सर्किट के चारों पक्षों में से प्रत्येक को घुमाने पर किए गए कार्य के बीजगणितीय योग के बराबर होता है:, जहां, शून्य के बराबर होते हैं, क्योंकि जब ये पक्ष चलते हैं तो चुंबकीय प्रवाह को पार नहीं करते हैं (शून्य क्षेत्र को रेखांकित करते हैं)। तार 1-2 प्रवाह में कटौती करता है, लेकिन चुंबकीय क्षेत्र की ताकतों के विपरीत चलता है। तब सामान्य कामसमोच्च आंदोलन द्वारा: या इधर सर्किट से जुड़े चुंबकीय प्रवाह में परिवर्तन है।

बी - चुंबकीय प्रेरण
μ0 - चुंबकीय स्थिरांक
मैं - वर्तमान शक्ति
आर - कंडक्टर से दूरी

एक वृत्ताकार धारा के केंद्र पर चुंबकीय क्षेत्र प्रेरण (मोड़)

बी - चुंबकीय प्रेरण
μ - सापेक्ष चुंबकीय पारगम्यता
μ0 - चुंबकीय स्थिरांक
मैं - वर्तमान शक्ति
आर - त्रिज्या

चुंबकीय क्षेत्र की ताकतएक सदिश राशि कहलाती है जो चुंबकीय क्षेत्र की विशेषता बताती है और इसे इस प्रकार परिभाषित किया गया है:

चुंबकीय क्षेत्र की ताकत: अनंत सीधा तार

मैं - वर्तमान ताकत
आर - कंडक्टर से दूरी

कुंडली के केंद्र पर चुंबकीय क्षेत्र की ताकत

एच - चुंबकीय क्षेत्र की ताकत

मैं - वर्तमान ताकत
आर - त्रिज्या

बायोट-सावर्ट-लाप्लास कानून.

बायोट-सावर्ट-लाप्लास का नियम- किसी भी धारा के चुंबकीय क्षेत्र की गणना धाराओं के अलग-अलग वर्गों द्वारा बनाए गए क्षेत्रों के वेक्टर योग के रूप में की जा सकती है।

सूत्रीकरण

निर्वात में स्थित एक समोच्च γ के साथ एक प्रत्यक्ष धारा प्रवाहित होने दें - वह बिंदु जिस पर क्षेत्र की मांग की जाती है, तो इस बिंदु पर चुंबकीय क्षेत्र प्रेरण अभिन्न (एसआई प्रणाली में) द्वारा व्यक्त किया जाता है

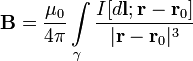
दिशा लंबवत है और, यानी, उस विमान के लंबवत है जिसमें वे झूठ बोलते हैं, और चुंबकीय प्रेरण की रेखा के स्पर्शरेखा के साथ मेल खाते हैं। यह दिशा चुंबकीय प्रेरण रेखाओं (दाएं हाथ के पेंच नियम) को खोजने के नियम द्वारा पाई जा सकती है: पेंच सिर के घूमने की दिशा दिशा देती है यदि गिम्लेट का अनुवादकीय आंदोलन तत्व में वर्तमान की दिशा से मेल खाता है . वेक्टर का परिमाण अभिव्यक्ति द्वारा निर्धारित किया जाता है (एसआई प्रणाली में)

वेक्टर क्षमता अभिन्न (SI में) द्वारा दी गई है

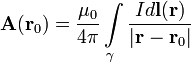
एकत्रीकरण की विभिन्न अवस्थाओं में पदार्थ की संरचना की आणविक-गतिज अवधारणाएँ।

मल्टीपार्टिकल सिस्टम की स्थिति और व्यवहार का वर्णन करने के लिए एक सांख्यिकीय विधि।

अवस्था के अनुसार आदर्श गैस अणुओं का वितरण:

जो शरीर हमें घेरे हुए हैं (ठोस, तरल, गैसीय) उन्हें हमारी इंद्रियां ठोस मानती हैं। हालाँकि, पिंड ठोस नहीं हैं, बल्कि नग्न आंखों के लिए अदृश्य छोटे कणों से बने हैं, जो एक दूसरे के करीब नहीं, बल्कि कुछ दूरी पर स्थित हैं। पदार्थ के इन सबसे छोटे कणों को अणु कहा जाता है (लैटिन शब्द "द्रव्यमान" से छोटा)।

डेमोक्रिटस (5वीं शताब्दी ईसा पूर्व) ने सबसे छोटे कणों को कहा जो दुनिया के सभी पिंडों को परमाणु (अविभाज्य) बनाते हैं। डेमोक्रिटस के अनुसार, परमाणुओं में होता है विभिन्न आकार, वजन, आकार, आदि।

1) सभी पदार्थ छोटे-छोटे कणों-अणुओं से बने होते हैं। अणु किसी पदार्थ का वह सबसे छोटा कण है जो उसके सभी तत्वों को बरकरार रखता है रासायनिक गुण. सभी अणु जो बनते हैं यह पदार्थ, बिलकुल वैसे ही हैं. अणु परमाणुओं से बने होते हैं। परमाणु सबसे छोटा कण है रासायनिक तत्व(105 टुकड़े - 94 प्राकृतिक और 11 कृत्रिम)।

2) शरीर के अणुओं के बीच परस्पर आकर्षण और प्रतिकर्षण बल एक साथ कार्य करते हैं।

3) पिंड बनाने वाले अणु निरंतर यादृच्छिक गति (दोलन) की स्थिति में हैं।

शरीर का तापमान जितना अधिक होगा, अणु उतनी ही तेजी से गति करेंगे। तापमान औसत का माप है गतिज ऊर्जाशरीर के अणु. शरीर के अणुओं की गति की गति, जो गतिज ऊर्जा निर्धारित करती है, शरीर की तापीय स्थिति और उसकी आंतरिक ऊर्जा की मात्रा निर्धारित करती है। अणुओं की अराजक गति को थर्मल कहा जाता है।

किसी अणु का परमाणुओं में विभाजित होना पृथक्करण कहलाता है। पृथक्करण 1 के प्रभाव में होता है) उच्च तापमान, 2) रासायनिक प्रतिक्रिएं, 3) विकिरण।

थर्मोडायनामिक्स कणों के अध्ययन के दो तरीकों पर आधारित है: थर्मोडायनामिक और स्टेटिक।

मैक्रोबॉडी बनाने वाले बड़ी संख्या में अणुओं के व्यवहार का अध्ययन एक सांख्यिकीय विधि द्वारा किया जाता है, जो इस तथ्य पर आधारित है कि मैक्रोबॉडी के गुण अणुओं के गुणों, उनके आंदोलन की विशेषताओं (गति, ऊर्जा, गति) द्वारा निर्धारित होते हैं , आदि) और बातचीत। उदाहरण के लिए, तापमान को आणविक गति की औसत गतिज ऊर्जा के रूप में व्यक्त किया जा सकता है। सांख्यिकीय विधि थर्मल प्रक्रियाओं के तंत्र का एक विचार देती है, उन्हें मैक्रोबॉडी के अंदर से मानते हुए; यह थर्मोडायनामिक विधि को महत्वपूर्ण रूप से पूरक करती है। ऊष्मागतिकी के मूल नियमों का सांख्यिकीय अर्थ भी होता है।

एक गैस में जो संतुलन की स्थिति में है, अणुओं का एक निश्चित स्थिर (समय के साथ नहीं बदलने वाला) वेग वितरण स्थापित किया जाएगा, जो एक अच्छी तरह से परिभाषित सांख्यिकीय कानून का पालन करता है। यह नियम सैद्धांतिक रूप से मैक्सवेल द्वारा व्युत्पन्न किया गया था।

इस नियम को निकालते समय, मैक्सवेल ने माना कि गैस में बहुत कुछ होता है बड़ी संख्या मेंसमान तापमान पर यादृच्छिक तापीय गति की स्थिति में एन समान अणु। यह भी माना गया कि बाहरी क्षेत्र गैस पर कार्य नहीं करते।

मैक्सवेल का नियम एक निश्चित फ़ंक्शन f(v) द्वारा वर्णित है, जिसे आणविक वेग वितरण फ़ंक्शन कहा जाता है। मैक्सवेल वितरण लिखने के तीन रूप हैं।

वृत्त में घूम रहे एक बिंदु पिंड के लिए न्यूटन का दूसरा नियम।

ध्यान में रखना ( ) और () बॉडी टॉर्क

यह अभिव्यक्ति घूर्णी गति के लिए न्यूटन के दूसरे नियम का एक एनालॉग है, जिससे यह पता चलता है कि कोणीय त्वरण ठोसएक निश्चित अक्ष के चारों ओर घूमते समय, यह टोक़ के सीधे आनुपातिक होता है और इस अक्ष के सापेक्ष जड़ता के क्षण के व्युत्क्रमानुपाती होता है। इस अभिव्यक्ति से यह पता चलता है कि जड़ता का क्षण यू एक निश्चित अक्ष के चारों ओर घूर्णी गति में इसकी जड़ता का माप है। स्थानांतरीय गति के मामले में, जड़ता का माप, जैसा कि ज्ञात है, शरीर का द्रव्यमान है।

उदाहरण दीजिए और उन बलों को इंगित कीजिए जो अभिकेन्द्रीय त्वरण का कारण बनते हैं।

ग्रहों का घूर्णन, जहां गुरुत्वाकर्षण एक अभिकेन्द्रीय बल के रूप में कार्य करता है। वहां कोई केन्द्रापसारक बल नहीं है. केन्द्रापसारक बल एक काल्पनिक बल है जिसे गणना में आसानी के लिए पेश किया जाता है, जब गैर-जड़त्वीय प्रणाली में गणना करना आसान होता है।

चुंबकीय क्षेत्र प्रवाह.

चुंबकीय प्रवाह (चुंबकीय प्रेरण लाइनों का प्रवाह)समोच्च के माध्यम से संख्यात्मक रूप से समोच्च द्वारा सीमित क्षेत्र और चुंबकीय प्रेरण वेक्टर की दिशा और इस समोच्च द्वारा सीमित सतह के सामान्य के बीच कोण के कोसाइन द्वारा चुंबकीय प्रेरण वेक्टर के परिमाण के उत्पाद के बराबर है।

जब कोई सीधा चालक गति करता है तो एम्पीयर बल के कार्य का सूत्र डीसीएक समान चुंबकीय क्षेत्र में.

इस प्रकार, एम्पीयर के बल द्वारा किए गए कार्य को स्थानांतरित कंडक्टर में वर्तमान और उस सर्किट के माध्यम से चुंबकीय प्रवाह में परिवर्तन के रूप में व्यक्त किया जा सकता है जिसमें यह कंडक्टर जुड़ा हुआ है:

लूप प्रेरण.

अधिष्ठापन- भौतिक मात्रा संख्यात्मक रूप से बराबर स्व-प्रेरित ईएमएफ, जो सर्किट में तब होता है जब करंट 1 सेकंड में 1 एम्पीयर बदल जाता है।
सूत्र का उपयोग करके प्रेरकत्व की गणना भी की जा सकती है:

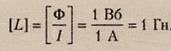जहां Ф सर्किट के माध्यम से चुंबकीय प्रवाह है, I सर्किट में वर्तमान ताकत है।

प्रेरण की एसआई इकाइयाँ:

चुंबकीय क्षेत्र ऊर्जा.

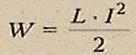चुंबकीय क्षेत्र में ऊर्जा होती है। जिस प्रकार चार्ज किए गए कैपेसिटर में रिजर्व होता है विद्युतीय ऊर्जा, जिस कुंडल के घुमावों से होकर धारा प्रवाहित होती है, उसमें चुंबकीय ऊर्जा का भंडार होता है।

पारंपरिक प्रकाश स्रोतों से प्रकाश हस्तक्षेप का कार्यान्वयन।

पतली फिल्म पर प्रकाश का हस्तक्षेप. परावर्तित और संचरित प्रकाश में फिल्म पर प्रकाश के अधिकतम और न्यूनतम हस्तक्षेप के लिए शर्तें।

समान मोटाई की व्यतिकरण फ्रिंज और समान झुकाव की व्यतिकरण फ्रिंज।

1) व्यवधान की घटना देखी गई है पतली परतअमिश्रणीय तरल पदार्थ (पानी की सतह पर मिट्टी का तेल या तेल), साबुन के बुलबुले में, गैसोलीन, तितली के पंखों पर, धूमिल रंगों में, आदि।

2) हस्तक्षेप तब होता है जब प्रकाश की एक मूल किरण गुजरते समय दो किरणों में विभाजित हो जाती है पतली फिल्म, उदाहरण के लिए, लेपित लेंस के लेंस की सतह पर लगाई गई एक फिल्म। मोटाई की फिल्म से गुजरने वाली प्रकाश की किरण दो बार परावर्तित होगी - इसकी आंतरिक और बाहरी सतहों से। परावर्तित किरणों में फिल्म की मोटाई के दोगुने के बराबर एक स्थिर चरण अंतर होगा, जिससे किरणें सुसंगत हो जाएंगी और हस्तक्षेप करेंगी। किरणों का पूर्ण शमन तरंग दैर्ध्य कहां पर होगा। यदि एनएम, तो फिल्म की मोटाई 550:4 = 137.5 एनएम है।

एनएम के दोनों किनारों पर स्पेक्ट्रम के पड़ोसी हिस्सों की किरणें पूरी तरह से हस्तक्षेप नहीं करती हैं और केवल क्षीण होती हैं, जिससे फिल्म रंग प्राप्त कर लेती है। ज्यामितीय प्रकाशिकी के सन्निकटन में, जब दो किरणों के लिए किरणों के पथ में ऑप्टिकल अंतर के बारे में बात करना समझ में आता है

अधिकतम स्थिति;

न्यूनतम शर्त

जहां k=0,1,2… और क्रमशः पहले और दूसरे बीम की ऑप्टिकल पथ लंबाई है।

3)समान ढलान वाली पट्टियाँ

विशेष रूप से महत्वपूर्ण विशेष मामलाजब अवलोकन बिंदु P अनंत पर होता है, तो समतल-समानांतर प्लेट की दो सतहों द्वारा परावर्तित प्रकाश का हस्तक्षेप। अवलोकन या तो अनंत तक समायोजित आंख से किया जाता है, या एकत्रित लेंस के फोकल तल में स्थित स्क्रीन पर किया जाता है (चित्र 8.8)।

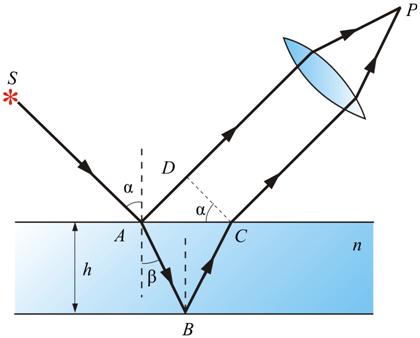
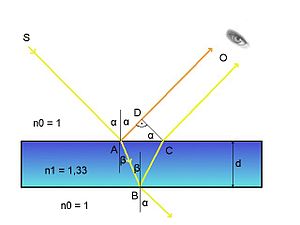
इस स्थिति में, S से P तक जाने वाली दोनों किरणें एक आपतित किरण द्वारा उत्पन्न होती हैं और, प्लेट की सामने और पीछे की सतहों से परावर्तन के बाद, एक दूसरे के समानांतर होती हैं। बिंदु P पर उनके बीच ऑप्टिकल पथ अंतर DC लाइन के समान है:

यहाँ n प्लेट सामग्री का अपवर्तनांक है। यह माना जाता है कि प्लेट के ऊपर हवा है, यानी। . क्योंकि 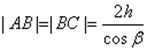, (एच प्लेट की मोटाई है, और ऊपरी सतह पर आपतन और अपवर्तन के कोण हैं;), फिर पथ अंतर के लिए हम प्राप्त करते हैं

12.7 चुंबकीय क्षेत्र प्रेरण की गणना।

बायोट-सावरे-लाप्लास कानून और सुपरपोजिशन सिद्धांत एक मनमाने सिस्टम द्वारा बनाए गए चुंबकीय क्षेत्र प्रेरण \(~\vec B\) की गणना करना संभव बनाता है विद्युत धाराएँ, अंतरिक्ष में एक मनमाने बिंदु पर। ऐसा करने के लिए, सभी धाराओं को अनंत छोटे वर्गों में विभाजित करना आवश्यक है \(~(I \Delta \vec l)_k\), क्षेत्र प्रेरण के लिए वैक्टर के लिए अभिव्यक्ति लिखें \(~(\Delta \vec B)_k\ ) इन तत्वों द्वारा निर्मित (बायोट-सावरे-लाप्लास कानून का उपयोग करके) और वर्तमान के सभी वर्गों के लिए परिणामी अभिव्यक्तियों का योग (जो सुपरपोजिशन के सिद्धांत की अनुमति देता है)

\(~\vec B = \sum_(k) ((\Delta \vec B)_k)\) . (1)

आइए कंडक्टर के करंट-वाहक अनुभाग को फिर से देखें (चित्र 29)। वर्तमान तत्व \(~I \Delta \vec l\) के लिए अभिव्यक्ति को \(~I \Delta \vec l = \vec j S \Delta l = \vec j \Delta V\) के रूप में भी लिखा गया है। उस स्थिति में जब विद्युत धाराएँ रैखिक नहीं होती हैं, बल्कि स्थानिक रूप से वितरित होती हैं (अर्थात, वे न केवल साथ-साथ बहती हैं पतले तार), वर्तमान तत्व \(~I \Delta \vec l\) के लिए अभिव्यक्ति को समतुल्य \(~\vec j \Delta V\) से प्रतिस्थापित किया जाना चाहिए और सभी वॉल्यूम तत्वों पर योग किया जाना चाहिए जहां विद्युत धाराएं होती हैं प्रवाह।

बेशक, ऐसा सारांश अक्सर एक बोझिल गणितीय समस्या होती है (आखिरकार, आप इसे करने के लिए कंप्यूटर का उपयोग कर सकते हैं), लेकिन भौतिक दृष्टिकोण से, प्रस्तुत विधि देती है संपूर्ण समाधानकार्य.

आइए ऊपर उल्लिखित विधि का उपयोग करके चुंबकीय क्षेत्र प्रेरण की गणना के कई उदाहरणों पर विचार करें।

12.7.1 वृत्ताकार धारा का चुंबकीय क्षेत्र।

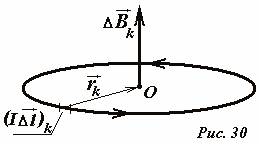
मान लीजिए विद्युत धारा स्थिर है मैंत्रिज्या के एक सपाट वृत्ताकार समोच्च के साथ बहती है आर. आइए हम रिंग के केंद्र बिंदु पर फ़ील्ड इंडक्शन का पता लगाएं हे(चित्र 30)। आइए मानसिक रूप से रिंग को छोटे-छोटे खंडों में विभाजित करें जिन्हें सीधा माना जा सकता है, और रिंग के केंद्र में इस तत्व द्वारा बनाए गए क्षेत्र के प्रेरण को निर्धारित करने के लिए बायोट-सावरे-लाप्लास कानून लागू करें। इस मामले में, वर्तमान तत्व का वेक्टर \(~(I \Delta \vec l)_k\) और इस तत्व को अवलोकन बिंदु (रिंग सेंटर) से जोड़ने वाला वेक्टर \(~\vec r_k\) लंबवत हैं, इसलिए \(\sin \ alpha = 1\) . रिंग के चयनित अनुभाग द्वारा बनाए गए क्षेत्र का प्रेरण वेक्टर रिंग की धुरी के साथ निर्देशित होता है, और इसका मापांक बराबर होता है

\(~\Delta B_k = \frac(\mu_0)(4 \pi) \frac((I \Delta l)_k)(R^2)\) . (1)

रिंग के किसी भी अन्य तत्व के लिए, स्थिति बिल्कुल समान है - इंडक्शन वेक्टर को रिंग की धुरी के साथ भी निर्देशित किया जाता है, और इसका मॉड्यूल सूत्र (1) द्वारा निर्धारित किया जाता है। इसलिए, इन वैक्टरों का योग प्राथमिक रूप से किया जाता है और रिंग के वर्गों की लंबाई के योग तक कम हो जाता है

\(~B = \sum_k \Delta B_k = \sum_k \frac(\mu_0)(4 \pi) \frac((I \Delta l)_k)(R^2) = \frac(\mu_0)(4 \ pi) \frac(I)(R^2) \sum_k (\Delta l)_k = \frac(\mu_0)(4 \pi) \frac(I)(R^2) 2 \pi R = \frac( \mu_0 I)(2 R)\) . (2)

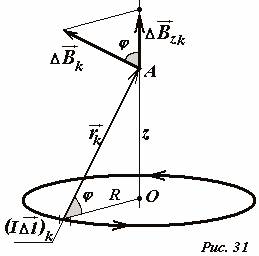
आइए समस्या को जटिल बनाएं - बिंदु पर फ़ील्ड इंडक्शन ढूंढें एकी दूरी पर वलय के अक्ष पर स्थित है जेडइसके केंद्र से (चित्र 31)। पहले की तरह, हम रिंग \(~(I \Delta \vec l)_k\) के एक छोटे से खंड का चयन करते हैं और इस तत्व द्वारा बनाए गए फ़ील्ड \(~(\Delta \vec B)_k\) के इंडक्शन वेक्टर का निर्माण करते हैं प्रश्नाधीन बिंदु पर. यह वेक्टर चयनित क्षेत्र को अवलोकन बिंदु से जोड़ने वाले वेक्टर \(~\vec r\) के लंबवत है। वेक्टर \(~(I \Delta \vec l)_k\) और \(~\vec r_k\), पहले की तरह, लंबवत हैं, इसलिए \(\sin \alpha = 1\) । तो अंगूठी है अक्षीय समरूपता, तो बिंदु पर क्षेत्र प्रेरण का कुल वेक्टर एरिंग की धुरी के साथ निर्देशित होना चाहिए। कुल प्रेरण वेक्टर की दिशा के बारे में एक ही निष्कर्ष पर पहुंचा जा सकता है यदि हम देखते हैं कि रिंग के प्रत्येक चयनित खंड में विपरीत दिशा में एक सममित है, और दो सममित वैक्टर का योग रिंग की धुरी के साथ निर्देशित है। इस प्रकार, कुल प्रेरण वेक्टर के मॉड्यूल को निर्धारित करने के लिए, रिंग के अक्ष पर वैक्टर के अनुमानों को जोड़ना आवश्यक है। यदि आप रिंग के सभी बिंदुओं से दूरियों पर विचार करें तो यह ऑपरेशन विशेष रूप से कठिन नहीं है अवलोकन बिंदुसमान हैं \(~r = r_k = \sqrt(R^2 + z^2)\) , और कोण भी समान हैं φ वैक्टर \(~(\Delta \vec B)_k\) और रिंग की धुरी के बीच। आइए हम वांछित कुल प्रेरण वेक्टर के मापांक के लिए अभिव्यक्ति लिखें

\(~B = \sum_k \Delta B_(zk) = \sum_k \frac(\mu_0)(4 \pi) \frac((I \Delta l)_k)(r^2) \cos \varphi = \frac (\mu_0)(4 \pi) \frac(I \cos \varphi)(r^2) \sum_k (\Delta l)_k = \frac(\mu_0)(4 \pi) \frac(I \cos \ varphi)(r^2) 2 \pi R = \frac(\mu_0 I R)(2 r^2) \cos \varphi\) .

चित्र से यह पता चलता है कि \(~\cos \varphi = \frac(R)(r)\), दूरी के लिए अभिव्यक्ति को ध्यान में रखते हुए आर, हम क्षेत्र प्रेरण वेक्टर के लिए अंतिम अभिव्यक्ति प्राप्त करते हैं

\(~B = \frac(\mu_0 I R)(2 r^2) \cos \varphi = \frac(\mu_0 I R^2)(2 r^3) = \frac(\mu_0 I)(2) \ cdot \frac(R^2)((R^2 + z^2)^\frac(3)(2))\) . (3)

जैसा कि कोई उम्मीद करेगा, रिंग के केंद्र में (at जेड= 0), सूत्र (3) पहले प्राप्त सूत्र (2) में बदल जाता है।

स्वतंत्र कार्य के लिए असाइनमेंट.

1. रिंग के केंद्र की दूरी पर फ़ील्ड इंडक्शन (3) की निर्भरता को प्लॉट करें।
2. प्राप्त निर्भरता (3) की तुलना एक समान रूप से चार्ज की गई रिंग (§9.6) द्वारा निर्मित विद्युत क्षेत्र की ताकत के मापांक की अभिव्यक्ति के साथ करें। इन निर्भरताओं के बीच मूलभूत अंतर स्पष्ट करें।

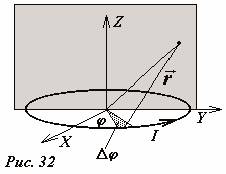
यहां चर्चा की गई सामान्य विधि का उपयोग करके, एक मनमाना बिंदु पर क्षेत्र प्रेरण की गणना करना संभव है। विचाराधीन प्रणाली में अक्षीय समरूपता है, इसलिए यह रिंग के विमान के लंबवत और उसके केंद्र से गुजरने वाले विमान में क्षेत्र वितरण को खोजने के लिए पर्याप्त है। अंगूठी को समतल में पड़ा रहने दें xOy(चित्र 32), और क्षेत्र की गणना समतल में की जाती है yOz. रिंग को केंद्र से Δ कोण पर दिखाई देने वाले छोटे-छोटे खंडों में विभाजित किया जाना चाहिए φ और इन अनुभागों द्वारा बनाए गए फ़ील्ड को सारांशित करें। आप प्रदर्शित करें ( खुद कोशिश करना), कि निर्देशांक के साथ बिंदु पर एक चयनित वर्तमान तत्व द्वारा बनाए गए क्षेत्र के चुंबकीय प्रेरण वेक्टर के घटक ( य,जेड) सूत्रों का उपयोग करके गणना की जाती है:

\(~\begin(matrix) r_k = \sqrt(x^2 + y^2 - 2xR \cos \varphi_k +1) ; \\ \Delta B_(yk) = -\frac(\mu_0)(4 \pi ) \frac(z \cos \varphi_k)(r^3_k) \Delta \varphi ; \\ \Delta B_(zk) = -\frac(\mu_0)(4 \pi) \frac(1 - y \cos \ varphi_k)(r^3_k) \Delta \varphi . \end(matrix)\) (4)

आवश्यक योग विश्लेषणात्मक रूप से नहीं किया जा सकता है, क्योंकि रिंग के एक खंड से दूसरे भाग में जाने पर, योग बिंदु की दूरियां बदल जाती हैं। इसलिए, इस तरह के सारांश को पूरा करने का "सरल" तरीका कंप्यूटर का उपयोग करना है।

यदि प्रत्येक बिंदु पर प्रेरण वेक्टर का मान ज्ञात है (या कम से कम इसकी गणना के लिए एक एल्गोरिदम है), तो चुंबकीय क्षेत्र रेखाओं की एक तस्वीर बनाना संभव है। यह स्पष्ट है कि एक वेक्टर क्षेत्र की बल रेखाओं के निर्माण के लिए एल्गोरिथ्म इसकी भौतिक सामग्री पर निर्भर नहीं करता है, और इलेक्ट्रोस्टैटिक्स का अध्ययन करते समय इस तरह के एल्गोरिदम पर हमारे द्वारा संक्षेप में चर्चा की गई थी।

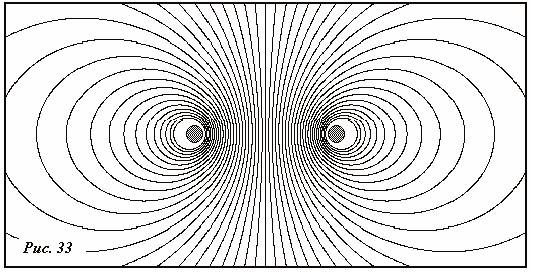
चित्र में. 33, रिंग को 20 भागों में विभाजित करके फ़ील्ड लाइनों के पैटर्न की गणना की गई; यह काफी पर्याप्त निकला, क्योंकि 10 डिवीजन अंतराल के साथ भी, लगभग एक ही पैटर्न प्राप्त हुआ था।

आइए रिंग की धुरी पर रिंग की त्रिज्या से काफी अधिक दूरी पर क्षेत्र प्रेरण के लिए अभिव्यक्ति पर विचार करें जेड >> आर. इस मामले में, सूत्र (3) सरल हो जाता है और रूप ले लेता है

\(~B = \frac(\mu_0 I)(2) \cdot \frac(R^2)((R^2 + z^2)^\frac(3)(2)) \लगभग \frac(\ mu_0 I)(2) \cdot \frac(R^2)(z^3) = \frac(\mu_0 I)(2 \pi) \cdot \frac(\pi R^2)(z^3) = \frac(\mu_0 p_m)(2 \pi z^3)\) , (5)

जहां \(I \pi R^2 = IS = p_m\) वर्तमान ताकत और सर्किट के क्षेत्र का उत्पाद है, यानी रिंग का चुंबकीय क्षण। यह सूत्र वही है (यदि, हमेशा की तरह, प्रतिस्थापित करें)। μ अंश में 0 ε हर में 0) अपनी धुरी पर द्विध्रुव की विद्युत क्षेत्र शक्ति के लिए एक अभिव्यक्ति के साथ।

यह संयोग आकस्मिक नहीं है; इसके अलावा, यह दिखाया जा सकता है कि ऐसा पत्राचार रिंग से बड़ी दूरी पर स्थित क्षेत्र के किसी भी बिंदु के लिए मान्य है। वास्तव में, धारा वाला एक छोटा सर्किट एक चुंबकीय द्विध्रुव (दो समान छोटे विपरीत निर्देशित धारा तत्व) है - इसलिए इसका क्षेत्र विद्युत द्विध्रुव के क्षेत्र के साथ मेल खाता है। इस तथ्य को अधिक स्पष्ट रूप से उजागर करने के लिए चित्र में दिखाया गया है। चित्र 34 रिंग की चुंबकीय क्षेत्र रेखाओं की एक तस्वीर दिखाता है, जो उससे बड़ी दूरी पर है ( विद्युत द्विध्रुवीय क्षेत्र के समान चित्र से तुलना करें).

12.7.2 प्रत्यक्ष धारा चुंबकीय क्षेत्र।

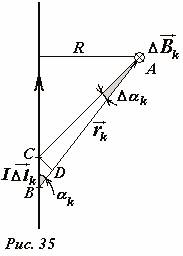
आइए हम एक अनंत चालक द्वारा निर्मित चुंबकीय क्षेत्र के प्रेरण की गणना करें जिसके माध्यम से बल के साथ विद्युत धारा प्रवाहित होती है मैं(चित्र 35) गणना पद्धति वही रहती है: हम मानसिक रूप से कंडक्टर को छोटे खंडों \(~I \Delta \vec l_k\) में विभाजित करते हैं। एक मनमाने बिंदु पर बायोट-सावरे-लाप्लास कानून के अनुसार ए, दूरी पर स्थित है आरएक कंडक्टर से, एक मनमाना वर्तमान तत्व एक चुंबकीय क्षेत्र बनाता है, जिसका प्रेरण वेक्टर \(~(\Delta \vec B)_k\) कंडक्टर वाले विमान और प्रश्न में बिंदु पर लंबवत निर्देशित होता है (चित्र 35 में) - आकृति के तल के लंबवत), इस वेक्टर का मापांक बराबर है

\(~\Delta B_k = \frac(\mu_0)(4 \pi) \frac(I \Delta l_k)(r^2_k) \sin \alpha_k\) , (1)

कहाँ आर k कंडक्टर के चयनित अनुभाग से अवलोकन बिंदु तक की दूरी है, α k कंडक्टर और वर्तमान तत्व से अवलोकन बिंदु तक की दिशा के बीच का कोण है।

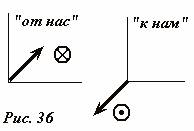
आइए एक और आम तौर पर स्वीकृत समझौते पर सहमत हों। अक्सर आपको ड्राइंग तल पर लंबवत सदिश खींचने पड़ते हैं। इस मामले में, इन वैक्टरों को इस रूप में दर्शाया गया है (चित्र 36): केंद्र में एक बिंदु के साथ एक छोटा वृत्त, यदि वेक्टर को "हम पर" निर्देशित किया जाता है (वेक्टर का "किनारा" दिखाई देता है); यदि वेक्टर हमसे दूर निर्देशित है तो क्रॉसहेयर वाला एक वृत्त (वेक्टर का "पंख" दिखाई देता है)।

कंडक्टर के अन्य सभी अनुभागों द्वारा बनाए गए फ़ील्ड वैक्टर भी निर्देशित होते हैं, इसलिए इस मामले में वैक्टर का योग उनके मॉड्यूल के योग तक कम हो जाता है। लेकिन मॉड्यूल के योग की गणना करना भी आसान नहीं है, क्योंकि कंडक्टर के विभिन्न वर्गों के लिए दूरियां होती हैं आरके और α k अलग हैं. फिर भी, ऐसा योग संभव है, इसका परिणाम एक सूत्र द्वारा व्यक्त किया जाता है जो अनंत आगे की धारा के चुंबकीय क्षेत्र प्रेरण के परिमाण को निर्धारित करता है

\(~B_k = \sum_k \Delta B_k = \sum_k \frac(\mu_0)(4 \pi) \frac(I \Delta l_k)(r^2_k) \sin \alpha_k = \frac(\mu_0 I)( 4 \pi) \sum_k (\frac(\Delta l_k)(r^2_k) \sin \alpha_k) = \frac(\mu_0 I)(2 \pi R)\) , (2)

अंतिम योग की गणना यहां नहीं दी गई है (जो \(~\sum_k \frac(\Delta l_k)(r^2_k) \sin \alpha_k = \frac(2)(R)\) के बराबर है), क्योंकि अब, परिणामी अभिव्यक्ति की वैधता पर विश्वास करें, यदि केवल इसलिए कि इसका एक समृद्ध भौतिक अर्थ है। सबसे पहले, यह सूत्र समान रूप से आवेशित धागे की एक अनंत सीधी रेखा द्वारा निर्मित विद्युत क्षेत्र की ताकत की अभिव्यक्ति से मेल खाता है; दूसरे, यह ए.एम. के प्रयोगों के परिणामों से मेल खाता है। समानांतर धाराओं की परस्पर क्रिया के अध्ययन पर एम्पीयर। वास्तव में, यदि एक कंडक्टर एक चुंबकीय क्षेत्र बनाता है, जिसका प्रेरण कंडक्टर से दूरी के व्युत्क्रमानुपाती होता है, तो दूसरे कंडक्टर पर क्षेत्र प्रेरण के आनुपातिक एम्पीयर बल द्वारा कार्य किया जाता है, अर्थात, बीच की दूरी के व्युत्क्रमानुपाती होता है। कंडक्टर.

आइए अब अभिव्यक्ति (2) में दिखाई देने वाली राशि के लिए सूत्र की एक कठोर व्युत्पत्ति दें। इसे एकीकरण के संचालन का उपयोग करके सबसे सरल रूप से प्राप्त किया जाता है, लेकिन यहां हम इसकी ज्यामितीय व्युत्पत्ति देंगे। आरंभ करने के लिए, चित्र का उपयोग करें। 35 हम इस सूत्र के प्रत्येक पद को \(~\frac(\Delta l_k)(r^2_k) \sin \alpha_k\) रूपांतरित करते हैं। ध्यान दें कि उत्पाद \(~\Delta l_k \sin \alpha_k\) खंड की लंबाई के बराबर है सीडी, वेक्टर के लंबवत \(~\vec r_k\) - \(~\Delta l_k \sin \alpha_k = |CD|\) । इस खंड की लंबाई और दूरी का अनुपात आरवर्तमान तत्वों की छोटी लंबाई के लिए k छोटे कोण Δ के बराबर है α k, जिसके अंतर्गत कंडक्टर का चयनित अनुभाग दिखाई देता है

\(~\frac(\Delta l_k)(r_k) \sin \alpha_k = \frac(|CD|)(r_k) = \Delta \alpha_k\) (3)

(अधिक सटीक रूप से, यह अनुपात कोण की स्पर्शरेखा के बराबर होता है, जो छोटे कोणों के लिए स्वयं कोण के बराबर होता है, जिसे रेडियन में मापा जाता है)। उसी आंकड़े से यह पता चलता है कि अनुपात \(~\frac(r_k)(\sin \alpha_k) = R\) अवलोकन बिंदु से कंडक्टर की दूरी के बराबर है और कंडक्टर अनुभाग की पसंद पर निर्भर नहीं करता है . इस संबंध और सूत्र (2) को ध्यान में रखते हुए, हम प्राप्त करते हैं

\(~\frac(\Delta l_k)(r^2_k) \sin \alpha_k = \frac(\Delta \alpha_k)(r_k) = \frac(\Delta \alpha_k \sin \alpha_k)(R)\) .

इस प्रकार, योग (2) की गणना करने से योग \(~\sum_k \Delta \alpha_k \sin \alpha_k\) की गणना कम हो जाती है, जिसमें सभी कोण छोटे होते हैं (इसलिए पदों की संख्या बड़ी होती है), मान लीजिए कि कोण α k शून्य से कुछ सीमित मान तक भिन्न होता है α अधिकतम.

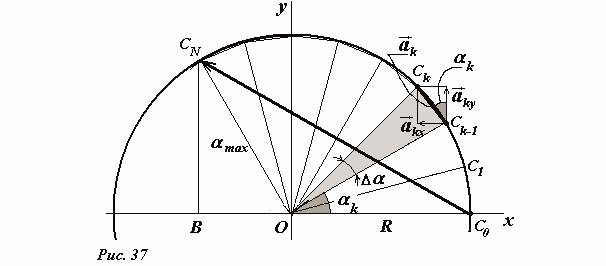
इस राशि की गणना करने के लिए, हम एक कृत्रिम तकनीक का उपयोग करेंगे (हम भविष्य में इसका सामना करेंगे)। आइए त्रिज्या का एक वृत्त लें (चित्र 37)। आरऔर इसे बिंदुओं से तोड़ें सी 0 , सी 1 , सी 2 , …, सीछोटे क्षेत्रों के लिए एन, कोणीय आकारप्रत्येक Δ के बराबर है α .

विभाजन बिंदुओं से बनने वाली जीवाओं को सदिश माना जाएगा \(~\vec a_0 = \overrightarrow (C_0 C_1), \vec a_1 = \overrightarrow (C_1 C_2), \ldots, \vec a_k = \overrightarrow (C_k C_(k+ 1)), \ldots\). इन सदिशों का योग स्पष्ट है - यह वृत्त विभाजन के आरंभ और समाप्ति बिंदुओं को जोड़ने वाला सदिश \(~\vec A\) है:

\(~\sum_k \vec a_k = \overrightarrow (C_0 C_N) = \vec A\) . (4)

अब, ध्यान दें, यदि वेक्टर समानता सत्य है, तो इन वैक्टरों के किसी भी प्रक्षेपण के लिए एक समान अभिव्यक्ति मान्य है। आइए परिचय कराते हैं कार्तीय प्रणालीवृत्त के केंद्र, अक्ष पर मूल के साथ समन्वय करता है बैलजो शुरुआती बिंदु से होकर गुजरती है. निर्मित अंकित सदिशों की लंबाई \(~|\vec a_k| = R \Delta \alpha_k\) के बराबर है (अधिक सटीक रूप से, यह चाप की लंबाई है, लेकिन छोटे कोणों के लिए, संकुचन जीवा की लंबाई बढ़ जाती है चाप की लंबाई तक)। चित्र 37 से यह पता चलता है कि निर्देशांक अक्षों पर इस वेक्टर के प्रक्षेपण क्रमशः बराबर हैं,

\(~a_(kx) = -R \Delta \alpha_k \sin \alpha_k ; a_(ky) = R \Delta \alpha_k \cos \alpha_k\) .

हमें प्राप्त निर्देशांक अक्षों पर समानता (4) प्रक्षेपित करना

\(~\begin(matrix) (\vec A)_x = (\overrightarrow (C_0 C_N))_x = -|C_0 B| = \sum_k a_(kx) = -\sum_k R \Delta \alpha_k \sin \alpha_k \\ (\vec A)_y = (\overrightarrow (C_0 C_N))_y = -|C_N B| = \sum_k a_(ky) = \sum_k R \Delta \alpha_k \cos \alpha_k \end(matrix) \) . (5)

निर्देशांक अक्षों पर कुल सदिश \(~\vec A\) के प्रक्षेपण आसानी से पाए जाते हैं

\(~\begin(matrix) (\vec A)_x = (\overrightarrow (C_0 C_N))_x = -|C_0 B| = -(R + R \cos (\pi - \alpha_(max))) = R(1 - \cos \alpha_(max)) \\ (\vec A)_y = (\overrightarrow (C_0 C_N))_y = -|C_N B| = R \sin (\pi - \alpha_(max)) = R \sin \alpha_(max) \end(matrix) \) . (6)

व्यंजक (5) और (6) की तुलना करने पर हमें आवश्यक सूत्र प्राप्त होते हैं

\(~\sum_k \sin \alpha_k \Delta \alpha_k = 1 - \cos \alpha_(max); \sum_k \cos \alpha_k \Delta \alpha_k = \sin \alpha_(max)\) . (7)

आइए हम एक बार फिर इस बात पर जोर दें कि इन सूत्रों में योग शून्य से सीमित मान तक कोण परिवर्तन की सीमा के भीतर किया जाता है α अधिकतम.

यह ध्यान में रखना बाकी है कि एक अनंत सीधा कंडक्टर एक कोण पर इसके बाहर किसी भी बिंदु से दिखाई देता है α अधिकतम = π , इसलिए आवश्यक राशि सूत्र द्वारा व्यक्त की जाती है

\(~\sum_k \frac(\Delta l_k)(r^2_k) \sin \alpha_k = \sum_k \frac(\Delta \alpha_k \sin \alpha_k)(R) = \frac(1 - \cos \pi) (आर) = \frac(2)(आर)\) ,

क्यू.ई.डी.

आइए इस मामले में "अनंत" कंडक्टर की लंबाई का अनुमान लगाएं - कंडक्टर की लंबाई अवलोकन बिंदु की दूरी से कितनी गुना अधिक होनी चाहिए ताकि सूत्र (2) का उपयोग करके क्षेत्र प्रेरण की गणना करने में त्रुटि हो परिमित लंबाई का चालक नगण्य होगा।

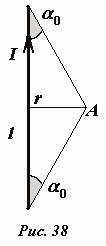
माना कि सीधे चालक की लंबाई है एल, और क्षेत्र प्रेरण की गणना बिंदु पर की जाती है ए, दूरी पर स्थित है आर(ऐसा हमारा विश्वास है आर << एल) कंडक्टर के केंद्र से (चित्र 38)। प्राप्त सूत्रों का उपयोग करके, कोई विचाराधीन बिंदु पर क्षेत्र प्रेरण के लिए एक सटीक अभिव्यक्ति प्राप्त कर सकता है \(~\bar(B) = \frac(\mu_0 I)(2 \pi r) \cos \alpha_0\) , जहां α 0 - कंडक्टर के बीच का कोण और कंडक्टर के अंत से अवलोकन बिंदु की दिशा।

यदि हम कंडक्टर को अनंत रूप से लंबा मानते हैं, तो फ़ील्ड इंडक्शन की गणना सूत्र का उपयोग करके की जानी चाहिए (जिसे इस मामले में अनुमानित माना जाना चाहिए) \(~\tilde(B) = \frac(\mu_0 I)(2 \pi आर)\) । इस सूत्र की सापेक्ष त्रुटि बराबर है

\(~\varepsilon = \frac(\tilde(B) - \bar(B))(\bar(B)) = \frac(1)(\cos \alpha_0) - 1 = \frac(\sqrt(\ बाएँ (\frac(l)(2) \right)^2 + r^2))(\frac(l)(2)) - 1 = \sqrt(1 + 4 \frac(r^2)(l^ 2)) - 1 \लगभग 2 \frac(r^2)(l^2)\) .

ऐसी त्रुटि तब होगी यदि कंडक्टर की लंबाई और अवलोकन बिंदु की दूरी का अनुपात \(~\frac(l)(r) = \frac(2)(\varepsilon)\) के बराबर हो। तो सापेक्ष त्रुटि के लिए ε = 1% आवश्यक अनुपात \(~\frac(l)(r) \लगभग 15\) है। तो, विचार किए गए मामले में, "अनंत" 15 के बराबर है।