Nilai eigen (angka) dan vektor eigen.
Contoh solusi

Jadilah diri sendiri

Dari kedua persamaan berikut ini.

Mari kita jelaskan: .

Sebagai akibat: – vektor eigen kedua.

Mari kita ulangi poin-poin penting dari keputusan tersebut:

– sistem yang dihasilkan pasti mempunyai solusi umum (persamaannya bergantung linier);

– kita memilih “y” sedemikian rupa sehingga bilangan bulat dan koordinat “x” pertama adalah bilangan bulat, positif dan sekecil mungkin.

– kita memeriksa bahwa solusi tertentu memenuhi setiap persamaan sistem.

Menjawab .

Terdapat cukup banyak “pos pemeriksaan” perantara, jadi pada prinsipnya pemeriksaan kesetaraan tidak diperlukan.

Dalam berbagai sumber informasi, koordinat vektor eigen seringkali ditulis bukan dalam kolom, melainkan dalam baris, misalnya: (dan sejujurnya saya sendiri sudah terbiasa menuliskannya dalam baris-baris). Opsi ini dapat diterima, namun sesuai dengan topiknya transformasi linier secara teknis lebih nyaman digunakan vektor kolom.

Mungkin solusinya terasa sangat panjang bagi Anda, tetapi ini hanya karena saya mengomentari contoh pertama dengan sangat rinci.

Contoh 2

Matriks

Ayo berlatih sendiri! Contoh perkiraan tugas akhir di akhir pembelajaran.

Terkadang Anda perlu menyelesaikan tugas tambahan, yaitu:

tulis dekomposisi matriks kanonik

Apa itu?

Jika vektor eigen dari matriks terbentuk dasar, maka dapat direpresentasikan sebagai:

Dimana matriks terdiri dari koordinat vektor eigen, – diagonal matriks dengan nilai eigen yang sesuai.

Dekomposisi matriks ini disebut resmi atau diagonal.

Mari kita lihat matriks pada contoh pertama. Vektor eigennya independen linier(non-collinear) dan membentuk basis. Mari kita buat matriks koordinatnya:

Pada diagonal utama matriks dalam urutan yang sesuai nilai eigen berada, dan elemen lainnya sama dengan nol:
– Saya sekali lagi menekankan pentingnya keteraturan: “dua” berhubungan dengan vektor pertama dan oleh karena itu terletak di kolom pertama, “tiga” – dengan vektor ke-2.

Menggunakan algoritma biasa untuk mencari matriks terbalik atau Metode Gauss-Jordan kami menemukan . Tidak, itu bukan salah ketik! - di hadapan Anda ada peristiwa langka, seperti gerhana matahari, yang kebalikannya bertepatan dengan matriks aslinya.

Tetap menuliskan dekomposisi kanonik matriks:

Sistem dapat diselesaikan dengan menggunakan transformasi dasar, dan dalam contoh berikut kita akan menggunakan metode ini. Namun di sini metode “sekolah” bekerja lebih cepat. Dari persamaan ke-3 kita nyatakan: – substitusikan ke persamaan kedua:

Karena koordinat pertama adalah nol, kita memperoleh suatu sistem, dari setiap persamaan berikut ini.

Dan lagi perhatikan adanya wajib hubungan linier. Jika hanya solusi sepele yang diperoleh , maka nilai eigen yang ditemukan salah, atau sistem dikompilasi/diselesaikan dengan kesalahan.

Koordinat kompak memberi nilai

vektor eigen:

Dan sekali lagi, kami memeriksa apakah solusinya ditemukan memenuhi setiap persamaan sistem. Dalam paragraf berikutnya dan tugas selanjutnya, saya merekomendasikan untuk menganggap keinginan ini sebagai aturan wajib.

2) Untuk nilai eigen, dengan menggunakan prinsip yang sama, kita memperoleh sistem berikut:

Dari persamaan ke-2 sistem kita nyatakan: – substitusikan ke persamaan ketiga:

Karena koordinat “zeta” sama dengan nol, kita memperoleh suatu sistem dari setiap persamaan yang mengikuti ketergantungan linier.

Membiarkan

Memeriksa itu solusinya memenuhi setiap persamaan sistem.

Jadi, vektor eigennya adalah: .

3) Dan terakhir, sistem sesuai dengan nilai eigen:

Persamaan kedua terlihat paling sederhana, jadi mari kita nyatakan dan substitusikan ke persamaan ke-1 dan ke-3:

Semuanya baik-baik saja - hubungan linier telah muncul, yang kami substitusikan ke dalam ekspresi:

Hasilnya, “x” dan “y” dinyatakan melalui “z”: . Dalam prakteknya, tidak perlu untuk mencapai hubungan seperti itu; dalam beberapa kasus lebih mudah untuk mengekspresikan keduanya melalui atau dan melalui . Atau bahkan "melatih" - misalnya, "X" hingga "I", dan "I" hingga "Z"

Mari kita jelaskan:

Kami memeriksa apakah solusinya ditemukan memenuhi setiap persamaan sistem dan menulis vektor eigen ketiga

Menjawab: vektor eigen:

Secara geometris, vektor-vektor ini menentukan tiga arah spasial yang berbeda ("Disana dan kembali lagi"), yg mana transformasi linier mengubah vektor bukan nol (vektor eigen) menjadi vektor kolinear.

Jika kondisi tersebut memerlukan penemuan dekomposisi kanonik, maka hal ini dimungkinkan di sini, karena nilai eigen yang berbeda sesuai dengan vektor eigen independen linier yang berbeda. Membuat matriks dari koordinatnya, matriks diagonal dari relevan nilai eigen dan temukan matriks terbalik .

Jika, dengan syarat, Anda perlu menulis matriks transformasi linier berdasarkan vektor eigen, lalu kita berikan jawabannya dalam bentuk . Ada perbedaan, dan perbedaannya signifikan! Karena matriks ini merupakan matriks “de”.

Masalah dengan perhitungan yang lebih sederhana untuk Anda selesaikan sendiri:

Contoh 5

Temukan vektor eigen dari transformasi linier yang diberikan oleh matriks

Saat mencari bilangan Anda sendiri, usahakan untuk tidak sampai ke polinomial derajat 3. Selain itu, solusi sistem Anda mungkin berbeda dengan solusi saya - tidak ada kepastian di sini; dan vektor yang Anda temukan mungkin berbeda dari vektor sampel hingga proporsionalitas koordinatnya masing-masing. Misalnya, dan. Memang lebih estetis menyajikan jawaban dalam bentuk, tapi tidak apa-apa jika Anda berhenti pada pilihan kedua. Namun, ada batasan wajar untuk semuanya; versinya tidak lagi terlihat bagus.

Perkiraan contoh tugas akhir di akhir pelajaran.

Bagaimana cara mengatasi masalah jika ada banyak nilai eigen?

Algoritme umumnya tetap sama, tetapi memiliki karakteristiknya sendiri, dan disarankan untuk mempertahankan beberapa bagian solusi dalam gaya akademis yang lebih ketat:

Contoh 6

Temukan nilai eigen dan vektor eigen

Larutan

Tentu saja, mari kita gunakan huruf besar pada kolom pertama yang menakjubkan:

Dan, setelah memfaktorkan trinomial kuadrat:

Hasilnya, diperoleh nilai eigen yang dua di antaranya merupakan kelipatan.

Mari kita cari vektor eigennya:

1) Mari kita berurusan dengan seorang prajurit menurut skema yang “disederhanakan”:

Dari dua persamaan terakhir terlihat jelas persamaan yang tentunya harus disubstitusikan ke persamaan pertama sistem:

Anda tidak akan menemukan kombinasi yang lebih baik:
vektor eigen:

2-3) Sekarang kita singkirkan beberapa penjaga. Dalam hal ini mungkin saja terjadi baik dua atau satu vektor eigen. Terlepas dari banyaknya akar, kita substitusikan nilainya ke dalam determinan yang membawa kita selanjutnya sistem persamaan linear yang homogen:

Vektor eigen sebenarnya adalah vektor
sistem dasar solusi

Sebenarnya, sepanjang pelajaran kita tidak melakukan apa pun selain menemukan vektor-vektor sistem fundamental. Hanya saja untuk saat ini istilah tersebut tidak terlalu dibutuhkan. Ngomong-ngomong, para siswa pintar yang melewatkan topik dalam pakaian kamuflase persamaan homogen, akan terpaksa merokok sekarang.

Satu-satunya tindakan adalah menghapus garis tambahan. Hasilnya adalah matriks satu per tiga dengan “langkah” formal di tengahnya.
– variabel dasar, – variabel bebas. Oleh karena itu, ada dua variabel bebas ada juga dua vektor sistem fundamental.

Mari kita nyatakan variabel dasar dalam bentuk variabel bebas: . Pengganda nol di depan “X” memungkinkannya mengambil nilai apa pun (yang terlihat jelas dari sistem persamaan).

Dalam konteks masalah ini, akan lebih mudah untuk menulis solusi umum bukan dalam satu baris, tetapi dalam kolom:

Pasangan ini sesuai dengan vektor eigen:
Pasangan ini sesuai dengan vektor eigen:

Catatan : pembaca yang mahir dapat memilih vektor-vektor ini secara lisan - cukup dengan menganalisis sistem , tetapi diperlukan beberapa pengetahuan di sini: ada tiga variabel, peringkat matriks sistem- satu, yang artinya sistem keputusan mendasar terdiri dari 3 – 1 = 2 vektor. Namun, vektor yang ditemukan terlihat jelas bahkan tanpa sepengetahuan ini, murni pada tingkat intuitif. Dalam hal ini, vektor ketiga akan ditulis lebih “indah”: . Namun, saya memperingatkan Anda bahwa dalam contoh lain, pemilihan sederhana mungkin tidak dapat dilakukan, itulah sebabnya klausa tersebut ditujukan untuk orang yang berpengalaman. Selain itu, mengapa tidak mengambil, katakanlah, sebagai vektor ketiga? Bagaimanapun, koordinatnya juga memenuhi setiap persamaan sistem, dan vektor-vektornya independen linier. Opsi ini, pada prinsipnya, cocok, tetapi “bengkok”, karena vektor “lainnya” adalah kombinasi linier dari vektor-vektor sistem fundamental.

Menjawab: nilai eigen: , vektor eigen:

Contoh serupa untuk solusi independen:

Contoh 7

Temukan nilai eigen dan vektor eigen

Contoh perkiraan desain akhir di akhir pelajaran.

Perlu dicatat bahwa dalam contoh ke-6 dan ke-7 diperoleh rangkap tiga vektor eigen bebas linier, dan oleh karena itu matriks asli dapat direpresentasikan dalam dekomposisi kanonik. Tetapi raspberry seperti itu tidak terjadi di semua kasus:

Contoh 8

Larutan: Mari kita buat dan selesaikan persamaan karakteristiknya:

Mari kita perluas determinan di kolom pertama:

Kami melakukan penyederhanaan lebih lanjut sesuai dengan metode yang dipertimbangkan, menghindari polinomial derajat ketiga:

– nilai eigen.

Mari kita cari vektor eigennya:

1) Tidak ada kesulitan dengan root:

Jangan kaget, selain kit, ada juga variabel yang digunakan - tidak ada perbedaan di sini.

Dari persamaan ke-3 kita nyatakan dan substitusikan ke persamaan ke-1 dan ke-2:

Dari kedua persamaan berikut:

Biarkan kemudian:

2-3) Untuk beberapa nilai kita mendapatkan sistemnya .

Mari kita tuliskan matriks sistem dan, dengan menggunakan transformasi dasar, bawa ke bentuk bertahap:

Matriks diagonal mempunyai struktur yang paling sederhana. Timbul pertanyaan apakah mungkin menemukan basis yang matriks operator liniernya berbentuk diagonal. Dasar seperti itu memang ada.
Mari kita diberi ruang linier R n dan operator linier A yang bekerja di dalamnya; dalam hal ini, operator A mengambil R n ke dalam dirinya sendiri, yaitu A:R n → R n .

Definisi. Vektor bukan nol disebut vektor eigen dari operator A jika operator A diubah menjadi vektor kolinear, yaitu. Bilangan λ disebut nilai eigen atau nilai eigen dari operator A, yang bersesuaian dengan vektor eigen.
Mari kita perhatikan beberapa sifat nilai eigen dan vektor eigen.
1. Setiap kombinasi linier dari vektor eigen operator A yang bersesuaian dengan nilai eigen yang sama λ adalah vektor eigen dengan nilai eigen yang sama.
2. Vektor eigen operator A dengan nilai eigen berbeda berpasangan λ 1 , λ 2 , …, λ m bebas linier.
3. Jika nilai eigen λ 1 =λ 2 = λ m = λ, maka nilai eigen λ berhubungan dengan tidak lebih dari m vektor eigen bebas linier.

Jadi, jika terdapat n vektor eigen bebas linier , sesuai dengan nilai eigen yang berbeda λ 1, λ 2, ..., λ n, maka nilai-nilai tersebut bebas linier, oleh karena itu, nilai-nilai tersebut dapat diambil sebagai basis ruang R n. Mari kita cari bentuk matriks dari operator linier A berdasarkan vektor eigennya, yang mana kita akan bertindak dengan operator A berdasarkan vektor basis: Kemudian .
Jadi, matriks operator linier A berdasarkan vektor eigennya berbentuk diagonal, dan nilai eigen operator A berada di sepanjang diagonal.
Apakah ada basis lain yang matriksnya berbentuk diagonal? Jawaban atas pertanyaan ini diberikan oleh teorema berikut.

Dalil. Matriks operator linier A pada basis (i = 1..n) berbentuk diagonal jika dan hanya jika semua vektor basisnya merupakan vektor eigen dari operator A.

Aturan untuk mencari nilai eigen dan vektor eigen

. (*)

(1)
Di mana - matriks operator linier.

Sistem (1) mempunyai solusi bukan nol jika determinannya D sama dengan nol

Contoh 12. Operator linier A bekerja di R 3 menurut hukum, dimana x 1, x 2, .., x n adalah koordinat vektor di basis , , . Temukan nilai eigen dan vektor eigen dari operator ini.
Larutan. Kami membangun matriks operator ini:
.
Kami membuat sistem untuk menentukan koordinat vektor eigen:

Kami membuat persamaan karakteristik dan menyelesaikannya:

.
λ 1,2 = -1, λ 3 = 3.
Substitusikan λ = -1 ke dalam sistem, kita peroleh:
atau
Karena , maka ada dua variabel terikat dan satu variabel bebas.
Misalkan x 1 adalah bilangan tak diketahui bebas Kita selesaikan sistem ini dengan cara apa pun dan temukan solusi umum dari sistem ini: Sistem solusi fundamental terdiri dari satu solusi, karena n - r = 3 - 2 = 1.
Himpunan vektor eigen yang bersesuaian dengan nilai eigen λ = -1 berbentuk: , dengan x 1 adalah bilangan apa pun selain nol. Mari kita pilih satu vektor dari himpunan ini, misalnya dengan memasukkan x 1 = 1: .
Dengan alasan yang sama, kita menemukan vektor eigen yang sesuai dengan nilai eigen λ = 3: .
Dalam ruang R 3, basis terdiri dari tiga vektor bebas linier, tetapi kita hanya menerima dua vektor eigen bebas linier, yang darinya basis di R 3 tidak dapat dibuat. Akibatnya, kita tidak dapat mereduksi matriks A dari operator linier menjadi bentuk diagonal.

Contoh 13. Diberikan sebuah matriks .
1. Buktikan bahwa vektor adalah vektor eigen dari matriks A. Temukan nilai eigen yang sesuai dengan vektor eigen tersebut.
2. Temukan basis yang matriks A berbentuk diagonal.
Larutan.
1. Jika , maka merupakan vektor eigen

.
Vektor (1, 8, -1) merupakan vektor eigen. Nilai eigen λ = -1.
Matriks tersebut mempunyai bentuk diagonal dengan basis yang terdiri dari vektor-vektor eigen. Salah satunya terkenal. Mari kita temukan sisanya.
Kami mencari vektor eigen dari sistem:

Persamaan karakteristik: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Mari kita cari vektor eigen yang sesuai dengan nilai eigen λ = -3:

Pangkat matriks sistem ini adalah dua dan sama dengan banyaknya yang tidak diketahui, jadi sistem ini hanya mempunyai solusi nol x 1 = x 3 = 0. x 2 di sini bisa berupa apa pun selain nol, misalnya x 2 = 1. Jadi, vektor (0 ,1,0) adalah vektor eigen yang bersesuaian dengan λ = -3. Mari kita periksa:
.
Jika λ = 1, maka diperoleh sistemnya
Pangkat matriksnya adalah dua. Kami mencoret persamaan terakhir.
Misalkan x 3 adalah suatu bilangan tidak diketahui bebas. Maka x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Dengan asumsi x 3 = 1, kita mempunyai (-3,-9,1) - vektor eigen yang sesuai dengan nilai eigen λ = 1. Periksa:

.
Karena nilai eigennya nyata dan berbeda, maka vektor-vektor yang bersesuaian dengannya adalah bebas linier, sehingga dapat dijadikan basis dalam R 3 . Jadi, sebagai dasarnya , , matriks A berbentuk:
.
Tidak semua matriks operator linier A:R n → R n dapat direduksi menjadi bentuk diagonal, karena untuk beberapa operator linier mungkin terdapat kurang dari n vektor eigen bebas linier. Namun, jika matriksnya simetris, maka akar persamaan karakteristik multiplisitas m bersesuaian dengan tepat m vektor bebas linier.

Definisi. Matriks simetris adalah matriks persegi yang elemen-elemennya simetris terhadap diagonal utamanya adalah sama, yaitu .
Catatan. 1. Semua nilai eigen matriks simetris adalah nyata.
2. Vektor eigen suatu matriks simetris yang bersesuaian dengan nilai eigen berbeda berpasangan adalah ortogonal.
Sebagai salah satu dari banyak aplikasi peralatan yang dipelajari, kami mempertimbangkan masalah penentuan jenis kurva orde kedua.

Definisi 9.3. Vektor X ditelepon vektor eigen matriks A, jika ada nomor seperti itu λ, bahwa kesetaraan berlaku: A X= λ X, yaitu hasil melamar X transformasi linier yang ditentukan oleh matriks A, adalah perkalian vektor ini dengan bilangan λ . Nomor itu sendiri λ ditelepon nilai eigen matriks A.

Mengganti ke dalam rumus (9.3) x` j = λx j , kita memperoleh sistem persamaan untuk menentukan koordinat vektor eigen:

. (9.5)

Sistem homogen linier ini akan mempunyai solusi nontrivial hanya jika determinan utamanya adalah 0 (aturan Cramer). Dengan menuliskan kondisi ini dalam bentuk:

kita memperoleh persamaan untuk menentukan nilai eigen λ , ditelepon persamaan karakteristik. Secara singkat dapat direpresentasikan sebagai berikut:

| SEBUAH - λE | = 0, (9.6)

karena ruas kirinya memuat determinan matriks A-λE. Relatif polinomial | SEBUAH - λE| ditelepon polinomial karakteristik matriks A.

Sifat-sifat polinomial karakteristik:

1) Polinomial karakteristik suatu transformasi linier tidak bergantung pada pilihan basis. Bukti. (lihat (9.4)), tapi karena itu, . Jadi, tidak bergantung pada pilihan basis. Artinya | A-λE| tidak berubah ketika pindah ke basis baru.

2) Jika matriks A transformasi linier adalah simetris(itu. dan ij =a ji), maka semua akar persamaan karakteristik (9.6) adalah bilangan real.

Sifat nilai eigen dan vektor eigen:

1) Jika Anda memilih basis dari vektor eigen x 1, x 2, x 3 , sesuai dengan nilai eigen λ 1, λ 2, λ 3 matriks A, maka dalam basis ini transformasi linier A mempunyai matriks berbentuk diagonal:

(9.7) Pembuktian sifat ini mengikuti definisi vektor eigen.

2) Jika nilai eigen transformasi A berbeda, maka vektor eigen yang bersesuaian adalah bebas linier.

3) Jika polinomial karakteristik matriks A memiliki tiga akar yang berbeda, maka dalam beberapa basis matriks A memiliki tampilan diagonal.

Mari kita cari nilai eigen dan vektor eigen dari matriks tersebut. Mari kita buat persamaan karakteristik: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Mari kita cari koordinat vektor eigen yang bersesuaian dengan setiap nilai yang ditemukan λ. Dari (9.5) berikut ini jika X (1) ={x 1 ,x 2 ,x 3) – vektor eigen yang sesuai λ 1 =-2, lalu

- sistem yang kooperatif tetapi tidak pasti. Solusinya dapat ditulis dalam bentuk X (1) ={A,0,-A), di mana a adalah bilangan apa pun. Khususnya, jika kita memerlukan | X (1) |=1, X (1) =

Mengganti ke dalam sistem (9.5) λ 2 =3, kita memperoleh sistem untuk menentukan koordinat vektor eigen kedua - X (2) ={kamu 1 ,kamu 2 ,kamu 3}:

, Di mana X (2) ={b,-b,b) atau, asalkan | X (2) |=1, X (2) =

Untuk λ 3 = 6 carilah vektor eigennya X (3) ={z 1 , z 2 , z 3}:

, X (3) ={C,2c,c) atau dalam versi yang dinormalisasi

x (3) = Hal ini dapat diperhatikan X (1) X (2) = ab–ab= 0, X (1) X (3) = ac-ac= 0, X (2) X (3) = SM- 2SM + SM= 0. Jadi, vektor eigen matriks ini ortogonal berpasangan.

Kuliah 10.

Bentuk kuadrat dan hubungannya dengan matriks simetris. Sifat-sifat vektor eigen dan nilai eigen matriks simetris. Mengurangi bentuk kuadrat menjadi bentuk kanonik.

Definisi 10.1.Bentuk kuadrat variabel nyata x 1, x 2,…, xn disebut polinomial derajat kedua pada variabel-variabel tersebut yang tidak mengandung suku bebas dan suku derajat pertama.

Contoh bentuk kuadrat:

(N = 2),

(N = 3). (10.1)

Mari kita mengingat kembali definisi matriks simetris yang diberikan pada kuliah terakhir:

Definisi 10.2. Matriks persegi disebut simetris, jika , yaitu jika elemen-elemen matriks yang simetris terhadap diagonal utama adalah sama.

Sifat-sifat nilai eigen dan vektor eigen matriks simetris:

1) Semua nilai eigen matriks simetris adalah nyata.

Bukti (untuk N = 2).

Biarkan matriks A memiliki bentuk: . Mari kita buat persamaan karakteristik:

(10.2) Mari kita cari pembedanya:

Oleh karena itu, persamaan tersebut hanya memiliki akar real.

2) Vektor eigen matriks simetris bersifat ortogonal.

Bukti (untuk N= 2).

Koordinat vektor eigen dan harus memenuhi persamaan.

Vektor eigen suatu matriks persegi adalah vektor yang jika dikalikan dengan matriks tertentu akan menghasilkan vektor yang kolinear. Dengan kata sederhana, ketika suatu matriks dikalikan dengan vektor eigen, vektor eigen tetap sama, tetapi dikalikan dengan bilangan tertentu.

Definisi

Vektor eigen adalah vektor bukan nol V, yang bila dikalikan dengan matriks persegi M, akan bertambah sejumlah λ. Dalam notasi aljabar terlihat seperti:

M × V = λ × V,

dimana λ adalah nilai eigen dari matriks M.

Mari kita lihat contoh numerik. Untuk memudahkan pencatatan, bilangan-bilangan pada matriks akan dipisahkan dengan titik koma. Mari kita punya matriks:

• M = 0; 4;
• 6; 10.

Mari kalikan dengan vektor kolom:

• V = -2;

Saat kita mengalikan matriks dengan vektor kolom, kita juga mendapatkan vektor kolom. Dalam bahasa matematika yang ketat, rumus mengalikan matriks 2 × 2 dengan vektor kolom akan terlihat seperti ini:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 berarti elemen matriks M yang terletak pada baris pertama dan kolom pertama, dan M22 berarti elemen yang terletak pada baris kedua dan kolom kedua. Untuk matriks kita, elemen-elemen tersebut sama dengan M11 = 0, M12 = 4, M21 = 6, M22 10. Untuk vektor kolom, nilainya sama dengan V11 = –2, V21 = 1. Menurut rumus ini, kita memperoleh hasil perkalian matriks persegi dengan vektor sebagai berikut:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Untuk memudahkan, mari kita tulis vektor kolom menjadi satu baris. Jadi, kita mengalikan matriks persegi dengan vektor (-2; 1), menghasilkan vektor (4; -2). Jelasnya, ini adalah vektor yang sama dikalikan dengan λ = -2. Lambda dalam hal ini menunjukkan nilai eigen dari matriks.

Vektor eigen suatu matriks adalah vektor kolinear, yaitu suatu benda yang tidak berubah posisinya dalam ruang jika dikalikan dengan suatu matriks. Konsep kolinearitas dalam aljabar vektor mirip dengan istilah paralelisme dalam geometri. Dalam interpretasi geometris, vektor-vektor collinear adalah segmen-segmen berarah paralel dengan panjang berbeda. Sejak zaman Euclid, kita mengetahui bahwa satu garis memiliki jumlah garis sejajar yang tak terhingga, sehingga masuk akal untuk mengasumsikan bahwa setiap matriks memiliki jumlah vektor eigen yang tak terhingga.

Dari contoh sebelumnya terlihat jelas bahwa vektor eigen dapat berupa (-8; 4), dan (16; -8), dan (32, -16). Ini semua adalah vektor kolinear yang sesuai dengan nilai eigen λ = -2. Saat mengalikan matriks asli dengan vektor-vektor ini, kita akan tetap mendapatkan vektor yang berbeda dari aslinya sebanyak 2 kali. Oleh karena itu, ketika menyelesaikan masalah pencarian vektor eigen, yang perlu dicari hanyalah objek vektor bebas linier. Seringkali, untuk matriks berukuran n × n, terdapat sejumlah n vektor eigen. Kalkulator kami dirancang untuk analisis matriks persegi orde kedua, sehingga hampir selalu hasilnya akan menemukan dua vektor eigen, kecuali jika keduanya bertepatan.

Pada contoh di atas, kita mengetahui vektor eigen matriks asli terlebih dahulu dan menentukan bilangan lambda dengan jelas. Namun, dalam praktiknya, yang terjadi sebaliknya: nilai eigen ditemukan terlebih dahulu, baru kemudian vektor eigen.

Algoritma solusi

Mari kita lihat kembali matriks asli M dan coba cari kedua vektor eigennya. Jadi matriksnya terlihat seperti:

• M = 0; 4;
• 6; 10.

Pertama kita perlu menentukan nilai eigen λ, yang memerlukan penghitungan determinan matriks berikut:

• (0 − λ); 4;
• 6; (10 −λ).

Matriks ini diperoleh dengan mengurangkan λ yang tidak diketahui dari elemen-elemen pada diagonal utama. Penentunya ditentukan dengan menggunakan rumus standar:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Karena vektor kita harus bukan nol, kita menerima persamaan yang dihasilkan sebagai persamaan bergantung linier dan menyamakan determinan detA kita dengan nol.

(0 − λ) × (10 − λ) − 24 = 0

Mari kita buka tanda kurung dan dapatkan persamaan karakteristik matriksnya:

λ 2 − 10λ − 24 = 0

Ini adalah persamaan kuadrat standar yang perlu diselesaikan dengan menggunakan diskriminan.

D = b 2 − 4ac = (-10) × 2 − 4 × (-1) × 24 = 100 + 96 = 196

Akar diskriminannya adalah akar kuadrat(D) = 14, maka λ1 = -2, λ2 = 12. Sekarang untuk setiap nilai lambda kita perlu mencari vektor eigennya. Mari kita nyatakan koefisien sistem untuk λ = -2.

• M − λ × E = 2; 4;
• 6; 12.

Dalam rumus ini, E adalah matriks identitas. Berdasarkan matriks yang dihasilkan, kami membuat sistem persamaan linier:

2x + 4y = 6x + 12y,

dimana x dan y adalah elemen vektor eigen.

Mari kita kumpulkan semua tanda X di sebelah kiri dan semua tanda Y di sebelah kanan. Jelasnya - 4x = 8y. Bagilah ekspresi tersebut dengan - 4 dan dapatkan x = –2y. Sekarang kita dapat menentukan vektor eigen pertama dari matriks tersebut, dengan mengambil nilai apa pun yang tidak diketahui (ingat tak terhingga dari vektor eigen yang bergantung linier). Misalkan y = 1, maka x = –2. Oleh karena itu, vektor eigen pertama terlihat seperti V1 = (–2; 1). Kembali ke awal artikel. Objek vektor inilah yang kami kalikan matriksnya untuk mendemonstrasikan konsep vektor eigen.

Sekarang mari kita cari vektor eigen untuk λ = 12.

• M - λ × E = -12; 4
• 6; -2.

Mari kita buat sistem persamaan linear yang sama;

• -12x + 4y = 6x − 2y
• -18x = -6 tahun
• 3x = kamu.

Sekarang kita ambil x = 1, maka y = 3. Jadi, vektor eigen kedua terlihat seperti V2 = (1; 3). Saat mengalikan matriks asli dengan vektor tertentu, hasilnya akan selalu berupa vektor yang sama dikalikan 12. Di sinilah algoritma penyelesaian berakhir. Sekarang Anda tahu cara menentukan vektor eigen suatu matriks secara manual.

• penentu;
• jejak, yaitu jumlah elemen-elemen pada diagonal utama;
• rangking, yaitu jumlah maksimum baris/kolom yang bebas linier.

Program ini beroperasi sesuai dengan algoritma di atas, mempersingkat proses solusi sebanyak mungkin. Penting untuk diperhatikan bahwa dalam program lambda ditandai dengan huruf “c”. Mari kita lihat contoh numerik.

Contoh cara kerja program

Mari kita coba menentukan vektor eigen untuk matriks berikut:

• M = 5; 13;
• 4; 14.

Mari masukkan nilai-nilai ini ke dalam sel kalkulator dan dapatkan jawabannya dalam bentuk berikut:

• Peringkat matriks: 2;
• Penentu matriks: 18;
• Jejak matriks: 19;
• Perhitungan vektor eigen: c 2 − 19.00c + 18.00 (persamaan karakteristik);
• Perhitungan vektor eigen: 18 (nilai lambda pertama);
• Perhitungan vektor eigen: 1 (nilai lambda kedua);
• Sistem persamaan vektor 1: -13x1 + 13y1 = 4x1 − 4y1;
• Sistem persamaan vektor 2: 4x1 + 13y1 = 4x1 + 13y1;
• Vektor eigen 1: (1; 1);
• Vektor eigen 2 : (-3.25; 1).

Jadi, kami memperoleh dua vektor eigen yang bebas linier.

Kesimpulan

Aljabar linier dan geometri analitik adalah mata pelajaran standar untuk setiap jurusan teknik mahasiswa baru. Banyaknya vektor dan matriks sangat menakutkan, dan mudah sekali terjadi kesalahan dalam perhitungan yang rumit tersebut. Program kami akan memungkinkan siswa untuk memeriksa perhitungan mereka atau secara otomatis memecahkan masalah pencarian vektor eigen. Ada kalkulator aljabar linier lainnya di katalog kami; gunakanlah dalam studi atau pekerjaan Anda.

Bagian pertama menguraikan ketentuan-ketentuan minimal yang diperlukan untuk memahami kemometri, dan bagian kedua berisi fakta-fakta yang perlu diketahui untuk memahami lebih dalam tentang metode analisis multivariat. Pemaparan diilustrasikan dengan contoh-contoh yang dibuat di buku kerja Excel matriks.xls, yang menyertai dokumen ini.

Tautan ke contoh ditempatkan dalam teks sebagai objek Excel. Contoh-contoh ini bersifat abstrak; sama sekali tidak terikat dengan masalah kimia analitik. Contoh nyata penggunaan aljabar matriks dalam kemometri dibahas dalam teks lain yang mencakup berbagai aplikasi kemometri.

Kebanyakan pengukuran yang dilakukan dalam kimia analitik tidak dilakukan secara langsung, melainkan langsung tidak langsung. Artinya dalam percobaan, alih-alih nilai analit C (konsentrasi) yang diinginkan, diperoleh nilai lain X(sinyal), terkait tetapi tidak sama dengan C, mis. X(C) ≠ C. Sebagai aturan, jenis ketergantungan X(C) tidak diketahui, namun untungnya dalam kimia analitik sebagian besar pengukuran bersifat proporsional. Artinya dengan meningkatnya konsentrasi C dalam A kali, sinyal X akan meningkat dengan jumlah yang sama, mis. X(A C) = sebuah x(C). Selain itu, sinyalnya juga bersifat aditif, sehingga sinyal dari sampel yang mengandung dua zat dengan konsentrasi C 1 dan C 2 akan sama dengan jumlah sinyal dari masing-masing komponen, yaitu. X(C 1 + C 2) = X(C 1)+ X(C2). Proporsionalitas dan aditif bersama-sama memberi linearitas. Banyak contoh yang dapat diberikan untuk menggambarkan prinsip linearitas, tetapi cukup menyebutkan dua contoh yang paling mencolok - kromatografi dan spektroskopi. Ciri kedua yang melekat pada percobaan kimia analitik adalah banyak saluran. Peralatan analitik modern secara bersamaan mengukur sinyal untuk banyak saluran. Misalnya, intensitas transmisi cahaya diukur untuk beberapa panjang gelombang sekaligus, yaitu. jangkauan. Oleh karena itu, dalam percobaan kami menangani banyak sinyal X 1 , X 2 ,...., X n, mencirikan himpunan konsentrasi C 1 , C 2 , ..., C m zat yang ada dalam sistem yang diteliti.

Beras. 1 Spektrum

Jadi, eksperimen analitik bercirikan linearitas dan multidimensi. Oleh karena itu, akan lebih mudah untuk menganggap data eksperimen sebagai vektor dan matriks dan memanipulasinya menggunakan peralatan aljabar matriks. Keberhasilan pendekatan ini diilustrasikan oleh contoh yang ditunjukkan pada gambar, yang menyajikan tiga spektrum yang diambil pada 200 panjang gelombang dari 4000 hingga 4796 cm −1. Pertama ( X 1) dan kedua ( X 2) spektrum diperoleh untuk sampel standar yang diketahui konsentrasi dua zat A dan B: pada sampel pertama [A] = 0,5, [B] = 0,1, dan pada sampel kedua [A] = 0,2, [ B] = 0,6. Apa yang dapat dikatakan tentang sampel baru yang tidak diketahui, yang spektrumnya ditunjukkan X 3 ?

Mari kita pertimbangkan tiga spektrum eksperimental X 1 , X 2 dan X 3 sebagai tiga vektor berdimensi 200. Dengan menggunakan aljabar linier, kita dapat dengan mudah menunjukkannya X 3 = 0.1 X 1 +0.3 X 2, jadi sampel ketiga jelas hanya mengandung zat A dan B dengan konsentrasi [A] = 0,5×0,1 + 0,2×0,3 = 0,11 dan [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Informasi dasar

1.1 Matriks

Matriks disebut tabel angka persegi panjang, misalnya

Beras. 2 Matriks

Matriks dinotasikan dengan huruf kapital ( A), dan elemennya - dengan huruf kecil yang sesuai dengan indeks, mis. A aku j. Indeks pertama memberi nomor pada baris, dan indeks kedua memberi nomor pada kolom. Dalam kemometri, nilai maksimum suatu indeks biasanya dilambangkan dengan huruf yang sama dengan indeks itu sendiri, tetapi dengan huruf kapital. Oleh karena itu matriks A juga dapat ditulis sebagai ( A aku j , Saya = 1,..., SAYA; J = 1,..., J). Misalnya matriks SAYA = 4, J= 3 dan A 23 = −7.5.

Sepasang angka SAYA Dan J disebut dimensi matriks dan dinotasikan sebagai SAYA× J. Contoh matriks dalam kemometri adalah himpunan spektrum yang diperoleh SAYA sampel untuk J panjang gelombang.

1.2. Operasi paling sederhana dengan matriks

Matriks bisa saja kalikan dengan angka. Dalam hal ini, setiap elemen dikalikan dengan angka ini. Misalnya -

Beras. 3 Mengalikan matriks dengan angka

Dua matriks yang berdimensi sama dapat disusun elemen demi elemennya melipat Dan mengurangi. Misalnya,

Beras. 4 Penjumlahan matriks

Hasil perkalian dengan suatu bilangan dan penjumlahan diperoleh matriks yang berdimensi sama.

Matriks nol adalah matriks yang terdiri dari angka-angka nol. Itu ditunjuk HAI. Jelas sekali A+HAI = A, A−A = HAI dan 0 A = HAI.

Matriksnya bisa mengubah urutan. Selama operasi ini, matriks dibalik, mis. baris dan kolom ditukar. Transposisi ditandai dengan bilangan prima, A" atau indeks A T. Jadi, jika A = {A aku j , Saya = 1,..., SAYA; J = 1,...,J), Itu A t = ( A Ji , J = 1,...,J; saya = 1,..., SAYA). Misalnya

Beras. 5 Transposisi matriks

Jelas sekali bahwa ( A t) t = A, (A+B)T = SEBUAH t+ B T.

1.3. Perkalian matriks

Matriks bisa saja berkembang biak, tetapi hanya jika dimensinya sesuai. Mengapa demikian akan jelas dari definisinya. Produk matriks A, dimensi SAYA× K, dan matriks B, dimensi K× J, disebut matriks C, dimensi SAYA× J, yang elemennya berupa angka

Demikian untuk produknya AB perlu jumlah kolom pada matriks kiri A sama dengan jumlah baris pada matriks sebelah kanan B. Contoh produk matriks -

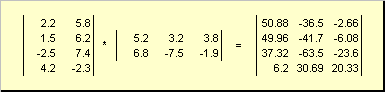
Gambar.6 Produk matriks

Aturan perkalian matriks dapat dirumuskan sebagai berikut. Untuk mencari elemen matriks C, berdiri di persimpangan Saya-baris ke-dan J kolom ke-( C aku j) harus dikalikan elemen demi elemen Saya-baris ke-th dari matriks pertama A pada J kolom ke-th dari matriks kedua B dan jumlahkan semua hasilnya. Jadi pada contoh yang ditunjukkan, elemen dari baris ketiga dan kolom kedua diperoleh sebagai jumlah dari hasil kali elemen baris ketiga. A dan kolom kedua B

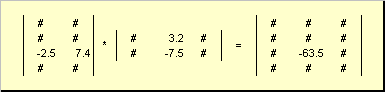
Gambar.7 Elemen produk matriks

Produk matriks tergantung pada pesanan, mis. AB ≠ B.A., setidaknya karena alasan dimensi. Mereka bilang itu non-komutatif. Namun, hasil kali matriks bersifat asosiatif. Artinya ABC = (AB)C = A(SM). Selain itu juga bersifat distributif, yaitu. A(B+C) = AB+AC. Jelas sekali A.O. = HAI.

1.4. Matriks persegi

Jika jumlah kolom matriks sama dengan jumlah barisnya ( SAYA = J=N), maka matriks seperti itu disebut persegi. Pada bagian ini kita hanya akan membahas matriks-matriks tersebut. Di antara matriks-matriks tersebut, dapat dibedakan matriks-matriks yang mempunyai sifat-sifat khusus.

Lajang matriks (dilambangkan SAYA, dan terkadang E) adalah matriks yang semua elemennya sama dengan nol, kecuali elemen diagonalnya sama dengan 1, yaitu.

Jelas sekali A.I. = I.A. = A.

Matriksnya disebut diagonal, jika semua elemennya kecuali diagonal ( A ii) sama dengan nol. Misalnya

Beras. 8 Matriks diagonal

Matriks A disebut bagian atas segitiga, jika semua elemennya yang terletak di bawah diagonal sama dengan nol, mis. A aku j= 0, pada Saya>J. Misalnya

Beras. 9 Matriks segitiga atas

Matriks segitiga bawah didefinisikan dengan cara yang sama.

Matriks A ditelepon simetris, Jika A t = A. Dengan kata lain A aku j = A Ji. Misalnya

Beras. 10 Matriks simetris

Matriks A ditelepon ortogonal, Jika

A T A = A A. t = SAYA.

Matriksnya disebut normal Jika

1.5. Jejak dan determinan

Berikutnya matriks persegi A(dilambangkan dengan Tr( A) atau Sp( A)) adalah jumlah elemen diagonalnya,

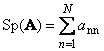
Misalnya,

Beras. 11 Jejak matriks

Jelas sekali

Sp(α A) = α Sp( A) Dan

Sp( A+B) = Sp( A)+ Sp( B).

Hal ini dapat ditunjukkan bahwa

Sp( A) = Sp( A t), Sp( SAYA) = N,

dan juga itu

Sp( AB) = Sp( B.A.).

Ciri penting lainnya dari matriks persegi adalah matriksnya penentu(dilambangkan det( A)). Menentukan determinan dalam kasus umum cukup sulit, jadi kita akan mulai dengan opsi paling sederhana - matriks A dimensi (2×2). Kemudian

Untuk matriks (3×3) determinannya sama dengan

Dalam kasus matriks ( N× N) determinannya dihitung sebagai jumlah 1·2·3· ... · N= N! syarat-syarat yang masing-masing sama

Indeks k 1 , k 2 ,..., k n didefinisikan sebagai semua kemungkinan permutasi terurut R bilangan dalam himpunan (1, 2, ..., N). Menghitung determinan suatu matriks merupakan prosedur yang rumit, yang dalam prakteknya dilakukan dengan menggunakan program khusus. Misalnya,

Beras. 12 Penentu matriks

Mari kita perhatikan hanya sifat-sifat yang jelas:

itu( SAYA) = 1, itu( A) = itu( A T),

itu( AB) = itu( A)itu( B).

1.6. vektor

Jika matriks hanya terdiri dari satu kolom ( J= 1), maka benda tersebut disebut vektor. Lebih tepatnya, vektor kolom. Misalnya

Kita juga dapat mempertimbangkan matriks yang terdiri dari satu baris, misalnya

Benda ini juga merupakan vektor, tetapi vektor baris. Saat menganalisis data, penting untuk memahami vektor mana yang kita hadapi - kolom atau baris. Jadi spektrum yang diambil untuk satu sampel dapat dianggap sebagai vektor baris. Kemudian himpunan intensitas spektral pada panjang gelombang tertentu untuk semua sampel harus diperlakukan sebagai vektor kolom.

Dimensi suatu vektor adalah jumlah elemen-elemennya.

Jelas bahwa setiap vektor kolom dapat diubah menjadi vektor baris dengan transposisi, yaitu.

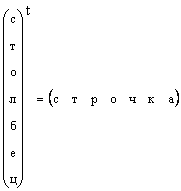
Dalam hal bentuk vektor tidak ditentukan secara spesifik, tetapi hanya dikatakan sebagai vektor, maka yang dimaksud adalah vektor kolom. Kami juga akan mematuhi aturan ini. Vektor dilambangkan dengan huruf kecil, tegak, dan tebal. Vektor nol adalah vektor yang semua elemennya nol. Itu ditunjuk 0 .

1.7. Operasi paling sederhana dengan vektor

Vektor dapat dijumlahkan dan dikalikan dengan bilangan seperti halnya matriks. Misalnya,

Beras. 13 Operasi dengan vektor

Dua vektor X Dan kamu disebut berbentuk kolinier, jika ada bilangan α sedemikian rupa

1.8. Produk vektor

Dua vektor berdimensi sama N dapat dilipatgandakan. Misalkan ada dua vektor X = (X 1 , X 2 ,...,X T)t dan kamu = (kamu 1 , kamu 2 ,...,kamu T) t . Dipandu oleh aturan perkalian baris demi kolom, kita dapat membuat dua hasil kali: X T kamu Dan xy T. Pekerjaan pertama

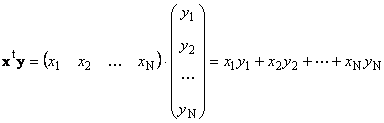
ditelepon skalar atau intern. Hasilnya adalah angka. Hal ini juga dilambangkan dengan ( X,kamu)= X T kamu. Misalnya,

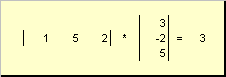
Beras. 14 Produk dalam (skalar).

Bagian kedua

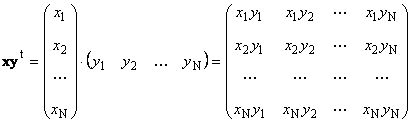
ditelepon luar. Hasilnya adalah matriks berdimensi ( N× N). Misalnya,

Beras. 15 Pekerjaan luar

Vektor yang hasil kali skalarnya nol disebut ortogonal.

1.9. Norma vektor

Hasil kali skalar suatu vektor dengan vektor itu sendiri disebut kuadrat skalar. Nilai ini

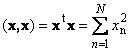
mendefinisikan persegi panjang vektor X. Untuk menunjukkan panjang (disebut juga norma vektor) notasi yang digunakan

Misalnya,

Beras. 16 Norma vektor

Vektor panjang satuan (|| X|| = 1) disebut dinormalisasi. Vektor bukan nol ( X ≠ 0 ) dapat dinormalisasi dengan membaginya dengan panjangnya, mis. X = ||X|| (X/||X||) = ||X|| e. Di Sini e = X/||X|| - vektor yang dinormalisasi.

Vektor disebut ortonormal jika semuanya ternormalisasi dan ortogonal berpasangan.

1.10. Sudut antar vektor

Produk skalar menentukan dan sudutφ antara dua vektor X Dan kamu

Jika vektor-vektornya ortogonal, maka cosφ = 0 dan φ = π/2, dan jika vektor-vektor tersebut kolinear, maka cosφ = 1 dan φ = 0.

1.11. Representasi vektor dari sebuah matriks

Setiap matriks A ukuran SAYA× J dapat direpresentasikan sebagai himpunan vektor

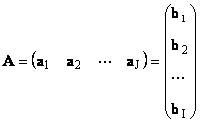
Di sini setiap vektor A J adalah J kolom ke-, dan vektor baris B Saya adalah Saya baris ke-matriks A

1.12. Vektor bergantung linier

Vektor berdimensi sama ( N) dapat dijumlahkan dan dikalikan dengan suatu bilangan, sama seperti matriks. Hasilnya akan menjadi vektor dengan dimensi yang sama. Misalkan ada beberapa vektor yang berdimensi sama X 1 , X 2 ,...,X K dan jumlah bilangan yang sama α α 1 , α 2 ,...,α K. Vektor

kamu= α 1 X 1 + α 2 X 2 +...+ α K X K

ditelepon kombinasi linear vektor X k .

Jika ada bilangan bukan nol α k ≠ 0, k = 1,..., K, Apa kamu = 0 , maka himpunan vektor tersebut X k ditelepon bergantung secara linear. Jika tidak, vektor-vektor tersebut dikatakan bebas linier. Misalnya vektor X 1 = (2, 2)t dan X 2 = (−1, −1) t bergantung linier, karena X 1 +2X 2 = 0

1.13. Peringkat matriks

Pertimbangkan satu set K vektor X 1 , X 2 ,...,X K ukuran N. Pangkat sistem vektor ini adalah jumlah maksimum vektor bebas linier. Misalnya di set

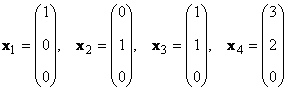
misalnya hanya ada dua vektor yang bebas linier X 1 dan X 2, jadi peringkatnya adalah 2.

Jelasnya, jika ada lebih banyak vektor dalam suatu himpunan daripada dimensinya ( K>N), maka keduanya bergantung linier.

Peringkat matriks(dilambangkan dengan peringkat( A)) adalah pangkat dari sistem vektor-vektor yang menyusunnya. Meskipun matriks apa pun dapat direpresentasikan dalam dua cara (vektor kolom atau baris), hal ini tidak mempengaruhi nilai peringkat, karena

1.14. matriks terbalik

Matriks persegi A disebut non-degenerasi jika mempunyai keunikan balik matriks A-1, ditentukan oleh kondisi

A A. −1 = A −1 A = SAYA.

Matriks invers tidak ada untuk semua matriks. Kondisi perlu dan cukup untuk non-degenerasi adalah

itu( A) ≠ 0 atau peringkat( A) = N.

Inversi matriks adalah prosedur kompleks yang memerlukan program khusus. Misalnya,

Beras. 17 Inversi matriks

Mari kita sajikan rumus untuk kasus paling sederhana - matriks 2×2

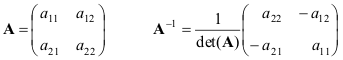
Jika matriks A Dan B kalau begitu, tidak merosot

(AB) −1 = B −1 A −1 .

1.15. Matriks pseudoinvers

Jika matriks A adalah tunggal dan matriks inversnya tidak ada, maka dalam beberapa kasus Anda dapat menggunakannya pseudoinvers matriks, yang didefinisikan sebagai matriks tersebut A+ itu

A A. + A = A.

Matriks pseudoinvers bukan satu-satunya dan bentuknya bergantung pada metode konstruksinya. Misalnya untuk matriks persegi panjang dapat menggunakan metode Moore-Penrose.

Jika jumlah kolom lebih kecil dari jumlah baris, maka

A + =(A T A) −1 A T

Misalnya,

Beras. 17a Inversi semu suatu matriks

Jika jumlah kolom lebih banyak dari jumlah baris, maka

A + =A T ( A A. T) −1

1.16. Mengalikan vektor dengan matriks

Vektor X dapat dikalikan dengan matriks A ukuran yang sesuai. Dalam hal ini, vektor kolom dikalikan ke kanan Kapak, dan baris vektor ada di sebelah kiri X T A. Jika berdimensi vektor J, dan dimensi matriks SAYA× J maka hasilnya akan menjadi vektor dimensi SAYA. Misalnya,

Beras. 18 Mengalikan vektor dengan matriks

Jika matriks A- persegi ( SAYA× SAYA), lalu vektornya kamu = Kapak mempunyai dimensi yang sama dengan X. Jelas sekali

A(α 1 X 1 + α 2 X 2) = 1 Kapak 1 + α 2 Kapak 2 .

Oleh karena itu, matriks dapat dianggap sebagai transformasi linier dari vektor. Secara khusus Ix = X, Sapi = 0 .

2. Informasi tambahan

2.1. Sistem persamaan linear

Membiarkan A- ukuran matriks SAYA× J, A B- vektor dimensi J. Pertimbangkan persamaannya

Kapak = B

relatif terhadap vektor X, dimensi SAYA. Pada dasarnya, ini adalah sebuah sistem SAYA persamaan linear dengan J tidak dikenal X 1 ,...,X J. Solusi ada jika dan hanya jika

pangkat( A) = peringkat( B) = R,

Di mana B adalah matriks dimensi yang diperluas SAYA×( J+1), terdiri dari matriks A, dilengkapi dengan kolom B, B = (A B). Jika tidak, persamaannya tidak konsisten.

Jika R = SAYA = J, maka solusinya unik

X = A −1 B.

Jika R < SAYA, maka ada banyak solusi berbeda yang dapat dinyatakan melalui kombinasi linier J−R vektor. Sistem persamaan homogen Kapak = 0 dengan matriks persegi A (N× N) mempunyai solusi nontrivial ( X ≠ 0 ) jika dan hanya jika det( A) = 0. Jika R= peringkat( A)<N, lalu ada N−R solusi bebas linier.

2.2. Bentuk bilinear dan kuadrat

Jika A adalah matriks persegi, dan X Dan kamu- vektor dari dimensi yang sesuai, maka produk skalar dari bentuknya X T Ay ditelepon bilinear bentuk yang ditentukan oleh matriks A. Pada X = kamu ekspresi X T Kapak ditelepon kuadrat membentuk.

2.3. Matriks pasti positif

Matriks persegi A ditelepon pasti positif, jika untuk sembarang vektor bukan nol X ≠ 0 ,

X T Kapak > 0.

Didefinisikan serupa negatif (X T Kapak < 0), non-negatif (X T Kapak≥ 0) dan negatif (X T Kapak≤ 0) matriks tertentu.

2.4. Dekomposisi Cholesky

Jika matriksnya simetris A adalah pasti positif, maka terdapat matriks segitiga unik kamu dengan unsur positif, untuk itu

A = kamu T kamu.

Misalnya,

Beras. 19 Dekomposisi Cholesky

2.5. Dekomposisi kutub

Membiarkan A adalah matriks persegi tak tunggal yang berdimensi N× N. Lalu ada yang unik kutub pertunjukan

A = S.R.

Di mana S adalah matriks simetris non-negatif, dan R adalah matriks ortogonal. Matriks S Dan R dapat didefinisikan secara eksplisit:

S 2 = A A. t atau S = (A A. t) ½ dan R = S −1 A = (A A. t) −½ A.

Misalnya,

Beras. 20 Dekomposisi kutub

Jika matriks A mengalami degenerasi, maka penguraiannya tidak unik yaitu: S masih sendirian, tapi R mungkin banyak. Dekomposisi polar mewakili matriks A sebagai kombinasi kompresi/ekstensi S dan berbalik R.

2.6. Vektor eigen dan nilai eigen

Membiarkan A adalah matriks persegi. Vektor ay ditelepon vektor eigen matriks A, Jika

Av = λ ay,

dimana bilangan λ disebut nilai eigen matriks A. Jadi, transformasi yang dilakukan matriks A di atas vektor ay, direduksi menjadi regangan atau kompresi sederhana dengan koefisien λ. Vektor eigen ditentukan hingga perkalian dengan konstanta α ≠ 0, yaitu. Jika ay adalah vektor eigen, maka α ay- juga merupakan vektor eigen.

2.7. Nilai eigen

Di matriks A, dimensi ( N× N) tidak boleh lebih dari N nilai eigen. Mereka memuaskan persamaan karakteristik

itu( A − λ SAYA) = 0,

yang merupakan persamaan aljabar N urutan -th. Khususnya, untuk matriks 2×2 persamaan karakteristiknya berbentuk

Misalnya,

Beras. 21 Nilai Eigen

Himpunan nilai eigen λ 1 ,..., λ N matriks A ditelepon spektrum A.

Spektrum mempunyai berbagai sifat. Secara khusus

itu( A) = λ 1 ×...×λ N,Sp( A) = λ 1 +...+λ N.

Nilai eigen suatu matriks sembarang dapat berupa bilangan kompleks, tetapi jika matriksnya simetris ( A t = A), maka nilai eigennya adalah real.

2.8. vektor eigen

Di matriks A, dimensi ( N× N) tidak boleh lebih dari N vektor eigen, yang masing-masing sesuai dengan nilai eigennya sendiri. Untuk menentukan vektor eigen ay N perlu menyelesaikan sistem persamaan homogen

(A − λ N SAYA)ay N = 0 .

Ini mempunyai solusi nontrivial, karena det( SEBUAH -λ N SAYA) = 0.

Misalnya,

Beras. 22 Vektor Eigen

Vektor eigen matriks simetris bersifat ortogonal.