Kompletter Wechselstromkreis

Bundesbehörde zum Thema Bildung in der Russischen Föderation

Kurchatov-Filiale

Staatliche Polytechnische Hochschule Kursk

Disziplin: „Elektrotechnik“

zum Thema: „Elektrische Schaltkreise Wechselstrom"

Ich habe die Arbeit erledigt:

Aseev Evgeniy Sergeevich

Student der Fachrichtung im 2. Jahr

"Atomstationen und Installationen"

Geprüft von: Gorlov A.N.

Kurtschatow

Einführung

Das Prinzip der Erzielung einer variablen EMF. Effektivwert von Strom und Spannung

Vektordiagramm-Methode

Wechselstromkreis mit aktivem Widerstand und Induktivität

Wechselstromkreis mit unterschiedlicher Belastung

Serienschaltung, enthaltend aktiver Widerstand, Induktivität und Kapazität

Resonanz von Spannungen und Strömen

Leitfähigkeit und Berechnung elektrischer Schaltkreise

Einführung

Bis zum Ende des 19. Jahrhunderts wurde ausschließlich auf Quellen zurückgegriffen Gleichstrom – chemische Elemente und Generatoren. Dies schränkte die Übertragungsmöglichkeiten ein elektrische Energie lange Distanzen. Um Verluste in Stromleitungen zu reduzieren, ist es bekanntermaßen notwendig, sehr hohe Spannungen zu verwenden. Allerdings ist es nahezu unmöglich, von einem Gleichstromgenerator eine ausreichend hohe Spannung zu erhalten. Das Problem der Übertragung elektrischer Energie über große Entfernungen wurde nur durch den Einsatz von Wechselstrom und Transformatoren gelöst.

1. Das Prinzip der Erzielung einer variablen EMF

Wechselstrom hat gegenüber Gleichstrom eine Reihe von Vorteilen: Ein Wechselstromgenerator ist viel einfacher und kostengünstiger als ein Gleichstromgenerator; Wechselstrom kann umgewandelt werden; Wechselstrom lässt sich leicht in Gleichstrom umwandeln; Wechselstrommotoren sind viel einfacher und billiger als Gleichstrommotoren.

Im Prinzip kann man als Wechselstrom jeden Strom bezeichnen, der seine Größe im Laufe der Zeit ändert, in der Technik ist Wechselstrom jedoch ein solcher Strom, der sowohl seine Größe als auch seine Richtung periodisch ändert. Darüber hinaus ist der Durchschnittswert der Stärke eines solchen Stroms über den Zeitraum T gleich Null. Der Wechselstrom wird als periodisch bezeichnet, weil er in Intervallen T charakterisiert ist physikalische Quantitäten Nehmen Sie die gleichen Werte an.

In der Elektrotechnik ist der sinusförmige Wechselstrom am weitesten verbreitet, d. h. ein Strom, dessen Wert nach dem Sinus- (oder Cosinus-)Gesetz variiert, was im Vergleich zu anderen periodischen Strömen eine Reihe von Vorteilen bietet.

Wechselstrom mit Industriefrequenz wird in Kraftwerken mit Wechselstromgeneratoren (dreiphasig) gewonnen Synchrongeneratoren). Das sind ziemlich komplexe elektrische Maschinen, betrachten wir es einmal physikalische Grundlage ihre Handlungen, d.h. die Idee, Wechselstrom zu erzeugen.

Lassen Sie ein gleichmäßiges Magnetfeld ein Dauermagnet ein Rahmen der Fläche S rotiert gleichmäßig mit einer Winkelgeschwindigkeit ω (Abb. 1).

Der magnetische Fluss durch den Rahmen ist gleich:

Ф=BS cosα (1.1)

wobei α der Winkel zwischen der Normalen zum Rahmen n und dem magnetischen Induktionsvektor B ist. Da sich bei gleichmäßiger Drehung des Rahmens ω= α/t der Winkel α gemäß dem Gesetz ändert α= ω t und Formel (1.1) wird die Form annehmen:

Ф=BScosωt (1.2)

Da sich der magnetische Fluss, der ihn durchquert, ständig ändert, wenn sich der Rahmen dreht, wird nach dem Gesetz der elektromagnetischen Induktion darin eine induzierte EMK E induziert:

E= -dФ/dt =BSωsinωt =E0sinωt (1.3)

wobei E0 = BSω die Amplitude der sinusförmigen EMK ist. Somit entsteht im Rahmen eine sinusförmige EMK, und wenn der Rahmen an eine Last angeschlossen ist, fließt ein sinusförmiger Strom im Stromkreis.

Die unter dem Sinus- oder Kosinuszeichen stehende Größe ωt = 2πt/Т = 2πft wird als Phase der durch diese Funktionen beschriebenen Schwingungen bezeichnet. Die Phase bestimmt den Wert der EMF zu jedem Zeitpunkt t. Die Phase wird in Grad oder Bogenmaß gemessen.

Die Zeit T einer vollständigen Änderung der EMK (dies ist die Zeit einer Umdrehung des Rahmens) wird als Periode der EMK bezeichnet. Die zeitliche Veränderung der EMF lässt sich in einem Zeitdiagramm darstellen (Abb. 2).

Der Kehrwert der Periode heißt Frequenz f = 1/T. Wird die Periode in Sekunden gemessen, so wird die Frequenz des Wechselstroms in Hertz gemessen. In den meisten Ländern, einschließlich Russland, beträgt die industrielle Wechselstromfrequenz 50 Hz (in den USA und Japan 60 Hz).

Die Größe der industriellen Wechselstromfrequenz wird durch technische und wirtschaftliche Überlegungen bestimmt. Ist er zu niedrig, vergrößern sich die Abmessungen elektrische Maschinen und folglich der Materialverbrauch für ihre Herstellung; Das Blinken des Lichts macht sich bemerkbar Glühbirne. Bei zu hohen Frequenzen nehmen die Energieverluste in den Kernen elektrischer Maschinen und Transformatoren zu. Als optimalste Frequenzen erwiesen sich daher 50–60 Hz. In einigen Fällen werden jedoch Wechselströme sowohl höherer als auch niedrigerer Frequenz verwendet. Flugzeuge nutzen beispielsweise eine Frequenz von 400 Hz. Bei dieser Frequenz ist es möglich, Größe und Gewicht von Transformatoren und Elektromotoren deutlich zu reduzieren, was für die Luftfahrt von größerer Bedeutung ist als eine Erhöhung der Verluste in den Kernen. An Eisenbahnen Verwenden Sie Wechselstrom mit einer Frequenz von 25 Hz und sogar 16,66 Hz.

Effektivwerte von Strom und Spannung

Um die Eigenschaften von Wechselstrom zu beschreiben, ist die Auswahl bestimmter physikalischer Größen erforderlich. Momentan- und Amplitudenwerte sind für diese Zwecke ungeeignet und die Durchschnittswerte über den Zeitraum sind Null. Daher wird das Konzept der Effektivwerte von Strom und Spannung eingeführt. Sie basieren auf der thermischen Wirkung des Stroms, unabhängig von seiner Richtung.

Die Effektivwerte von Strom und Spannung sind die entsprechenden Parameter eines Gleichstroms, bei dem in einem bestimmten Leiter über einen bestimmten Zeitraum die gleiche Wärmemenge freigesetzt wird wie bei Wechselstrom. Lassen Sie uns die Beziehung zwischen den Effektiv- und Amplitudenwerten ermitteln.

Im aktiven Widerstand R wird bei konstantem Strom I über einen Zeitraum konstanten Stroms T nach dem Joule-Lenz-Gesetz folgende Wärmemenge freigesetzt:

Bei Wechselstrom i im gleichen Widerstand R wird in einer verschwindend kleinen Zeitspanne dt folgende Wärmemenge freigesetzt:

dQ = i Rdt (1,5)

wobei der Momentanwert des Stroms i durch die Formel bestimmt wird:

i = I0sinωt (1.6)

Dann ist die vom Wechselstrom während der Periode T freigesetzte Wärme gleich:

Integral (1.7) wird wie folgt berechnet:

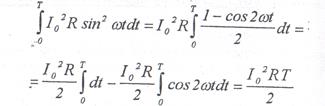
Das zweite Integral ist Null, weil es das Integral einer periodischen Funktion über eine Periode ist. Durch Gleichsetzung gemäß Definition (1.4) und (1.8) erhalten wir:

Somit ist der Effektivwert des Wechselstroms √2-mal kleiner Amplitudenwert. Die Effektivwerte von Spannung und EMK werden auf ähnliche Weise berechnet:

U = U0/√2; E = E0/√2 (1.10)

Gültige Werte werden in lateinischen Großbuchstaben ohne Indizes angegeben.

2. Vektordiagramm-Methode

Die Methode der Vektordiagramme ist die Darstellung von Größen, die Wechselstrom durch Vektoren charakterisieren, und nicht trigonometrische Funktionen, äußerst praktisch.

Wechselstrom wird im Gegensatz zu Gleichstrom durch zwei skalare Größen charakterisiert – Amplitude und Phase. Für eine mathematische Beschreibung des Wechselstroms ist daher ein mathematisches Objekt erforderlich, das ebenfalls durch zwei skalare Größen gekennzeichnet ist. Es gibt zwei solcher mathematischer Objekte – einen Vektor auf einer Ebene und eine komplexe Zahl. In der Theorie elektrischer Stromkreise werden beide zur Beschreibung von Wechselströmen verwendet.

Bei der Beschreibung eines Wechselstromkreises mithilfe von Vektordiagrammen ist jeder Strom und jede Spannung einem Vektor auf der Ebene in zugeordnet Polar Koordinaten, dessen Länge gleich der Amplitude des Stroms oder der Spannung ist und deren Polarwinkel gleich der entsprechenden Phase ist. Da die Phase des Wechselstroms von der Zeit abhängt, wird davon ausgegangen, dass sich alle Vektoren mit der Frequenz des Wechselstroms gegen den Uhrzeigersinn drehen. Ein Vektordiagramm wird für einen festen Zeitpunkt erstellt.

Der Aufbau und die Verwendung von Vektordiagrammen werden im Folgenden anhand von Beispielen konkreter Schaltungen näher beschrieben.

3. Wechselstromkreis mit aktivem Widerstand und Induktivität

Betrachten wir eine Schaltung (Abb. 3), bei der eine sinusförmige Spannung an einen aktiven Widerstand (Widerstand) angelegt wird:

U (t) = U0sin ωt (1.11)

Dann ist der Strom im Stromkreis nach dem Ohmschen Gesetz gleich:

I (t) = U (t)/R = U0sin ωt/R = I0 sin ωt (1.12)

Wir sehen, dass Strom und Spannung in Phase sind. Das Vektordiagramm für diese Schaltung ist in Abbildung 4 dargestellt:

Lassen Sie uns herausfinden, wie sich die Leistung in einem Wechselstromkreis mit einem Widerstand im Laufe der Zeit ändert. Der Momentanleistungswert ist gleich dem Produkt der Momentanwerte von Strom und Spannung:

p (t) = i(t)u(t) = I0 U0 sin ωt = I0 U0(1- cos2 ωt)/2 (1.13)

Aus dieser Formel sehen wir, dass die Momentanleistung immer positiv ist und mit der doppelten Frequenz pulsiert (Abb. 5):

Das bedeutet, dass elektrische Energie unabhängig von der Stromrichtung im Stromkreis irreversibel in Wärme umgewandelt wird.

Berechnen wir den durchschnittlichen Leistungswert für den Zeitraum:

Pav = 1/T ∫ p(t)dt = I0U0/2T ∫ dt − I0U0/2T ∫ cos2ωt dt = (I0U0/2T) ∙T = IU = I R

da das zweite Integral als Integral einer periodischen Funktion über einen Zeitraum gleich Null ist.

Wir sehen, dass in einem Stromkreis mit einem Widerstand die gesamte elektrische Energie irreversibel in umgewandelt wird Wärmeenergie. Diejenigen Schaltungselemente, an denen die irreversible Umwandlung elektrischer Energie in andere Energiearten (nicht nur thermische) stattfindet, werden aktive Widerstände genannt. Daher stellt der Widerstand den aktiven Widerstand dar.

Betrachten wir eine Schaltung (Abb. 6), in der eine sinusförmige Spannung (1.11) an die Induktivität L angelegt wird, die keinen aktiven Widerstand hat (R = 0):

Der durch die Spule fließende Wechselstrom erzeugt darin Selbstinduzierte EMK eL. Dann können wir gemäß Kirchhoffs zweiter Regel schreiben:

U + eL = 0 (1,15)

Nach dem Faradayschen Gesetz ist die selbstinduzierte EMK gleich:

eL = −LdI/dt (1.16)

Wenn wir (1.16) in (1.15) einsetzen, erhalten wir:

dI/dt = − eL/L = U/L = U0 sin ωt/L (1.17)

Wenn wir diese Gleichung integrieren, erhalten wir:

I =− U0cos ωt/ω L + const = U0sin (ωt − π/2)/ ωL+ const (1.18)

Dabei ist const die Integrationskonstante, die angibt, dass möglicherweise Gleichstrom im Stromkreis vorhanden ist. Ohne Gleichstrom ist er Null. Ohne Gleichstrom ist er Null. Endlich haben wir:

I = I0 sin (ωt − π/2) (1.19)

wobei I0 = U0/ ωL. Wenn wir beide Seiten durch √2 dividieren, erhalten wir:

I = U/ ωL= U/ XL (1.20)

Die Beziehung (1.20) stellt das Ohmsche Gesetz für einen Stromkreis mit idealer Induktivität dar, und der Wert XL= ωL wird als induktive Reaktanz bezeichnet.

Aus Formel (1.19) sehen wir, dass im betrachteten Stromkreis der Strom der Spannung um π/2 in Phase nacheilt. Das Zeigerdiagramm für diese Schaltung ist in Abbildung 7 dargestellt.

Berechnen wir die Leistung, die ein Stromkreis mit rein induktiver Reaktanz verbraucht.

Momentanleistung ist gleich:

p (t)= I0 U0 sin ωt(ωt − π/2)= − I0 U0 sin2 ωt/2 (1.21)

Wir sehen, dass es sich nach dem Sinusgesetz mit der doppelten Frequenz ändert (Abb. 8).

Positive Leistungswerte entsprechen dem Energieverbrauch der Spule und negative Werte entsprechen der Rückführung gespeicherter Energie zurück zur Quelle.

Die durchschnittliche Leistung über den Zeitraum beträgt:

Pav = 1/T ∫ p(t)dt = (− I0 U0 /2T) ∫ sin2 ωt dt = 0 (1.22)

Wir sehen, dass der Stromkreis mit Induktivität keinen Strom verbraucht – es handelt sich um eine reine Blindlast.

5. Wechselstromkreis mit unterschiedlicher Belastung

Wechselstromkreis mit aktiv-induktiver Last

Lassen Sie uns überlegen Stromkreis(Abb. 9), bei dem ein Wechselstrom durch eine Induktivität L mit einem Wirkwiderstand R fließt:

I = I0 sin ωt (1.23)

Die an den Stromkreis angelegte Spannung ist gleich der Vektorsumme der Spannungsabfälle an der Induktivität und dem Widerstand:

U = UL+UR (1,24)

Die Spannung am Widerstand ist, wie oben gezeigt, in Phase mit dem Strom:

UR = U0R sin ωt (1,25)

und die Spannung an der Induktivität ist gleich der selbstinduktiven EMK mit Minuszeichen (gemäß Kirchhoffs zweiter Regel):

UL = L(dI/dt)= I0 ωLcos ωt = U0Lsin(ωt + π/2) (1.26)

wobei U0L= I0 ωL (1.27)

Die Spannung an der Induktivität eilt dem Strom um π/2 voraus. Weiter zur Formel (1.27) zu aktuelle Werte Wechselstrom (I = I0/√2; U= U0/√2) erhalten wir:

I = UL/XL (1,28)

Dies ist das Ohmsche Gesetz für einen Stromkreis mit idealer Induktivität (d. h. ohne aktiven Widerstand), und der Wert XL = ωL wird als induktive Reaktanz bezeichnet. Indem wir die Vektoren I, UR und UL konstruieren und Formel (1.24) verwenden, finden wir den Vektor U.

U= √ UR + UL = √ I R + I (ωL) = I√ R + (ωL) = IZ (1.29)

Wo ist der Wert?

Z = √ R + (ωL) (1.30)

Außerdem wird daraus die Phasenverschiebung φ zwischen Strom und Spannung ermittelt Vektordiagramm:

tan φ = UL/ UR = ωL/ R (1.31)

In dieser Schaltung hängt der Phasenwinkel zwischen Strom und Spannung von den Werten von R und L ab und variiert von 0 bis π/2.

Schauen wir uns nun an, wie sich die Leistung in einem Stromkreis mit einer aktiv-induktiven Last im Laufe der Zeit ändert. Momentane Strom- und Spannungswerte können dargestellt werden als:

U(t) = U0 sin ωt (1.32)

I(t) = I0 sin(ωt − φ)

p(t)= I(t) U(t) = I0 U0 sin ωt sin(ωt − φ)=(I0 U0/2) = =(I0 U0/2)(1− cos2ωt) cosφ − (I0 U0/ 2) sin2ωt sinφ (1.33)

Der Momentanleistungswert besteht aus zwei Komponenten: Der erste Term ist aktiv und der zweite ist reaktiv (induktiv). Daher ist die durchschnittliche Leistung über den Zeitraum nicht Null:

Pav = 1/T ∫ pdt = (I0 U0/2T) cosφ ∫dt − (I0 U0/2T) cosφ ∫ cos2ωt dt −

−(I0 U0/2T) sin φ ∫ sin2ωt dt = (I0 U0/2) cosφ (1.34)

Wechselstromkreis mit Kapazität

Stellen Sie sich einen Stromkreis vor, in dem Wechselstrom Spannung(1.11) wird auf Behälter C angewendet (Abb. 11). Der Momentanwert des Stroms in einem Stromkreis mit einer Kapazität ist gleich der Ladungsrate auf den Kondensatorplatten:

I = dq/dt (1,35)

aber weil q = CU also

I = C (dU/dt) = ωCU0 cos ωt = I0 sin (ωt + π/2) (1.36)

ωCU0 = I0 (1,37)

In dieser Schaltung eilt der Strom der Spannung um π/2 voraus. Übergeben wir die Formel (1.37) an die Effektivwerte des Wechselstroms (I = I0/√2; U= U0/√2), erhalten wir:

I0 = U/Xc (1,38)

Dies ist das Ohmsche Gesetz für einen Wechselstromkreis mit einer Kapazität und der Menge

Xc= 1/ωC ​​​​wird als kapazitive Reaktanz bezeichnet. Das Vektordiagramm für diese Schaltung ist in Abb. dargestellt. 12.

Lassen Sie uns die momentane und durchschnittliche Leistung in einem Stromkreis ermitteln, der eine Kapazität enthält. Momentanleistung ist:

p(t)= i(t) u(t) = I0U0 sin (ωt + π/2) sin ωt = IUsin2 ωt (1.39)

Die Momentanleistung ändert sich mit der doppelten Frequenz (Abb. 13). Dabei positive Werte Leistungen entsprechen der Ladung des Kondensators und negative entsprechen seiner Entladung und der Rückkehr der gespeicherten Energie zur Quelle. Die durchschnittliche Leistung über den Zeitraum beträgt hier Null

Pav = 1/T ∫ p(t)dt = IU/T ∫ sin2 ωt dt = 0 (1.40)

Weil In einem Stromkreis mit einem Kondensator wird keine Wirkleistung verbraucht, sondern elektrische Energie zwischen dem Kondensator und der Quelle ausgetauscht.

Wechselstromkreis mit aktiv-kapazitiver Last

Ein echter Wechselstromkreis mit einer Kapazität enthält immer aktiven Widerstand – Drahtwiderstand, aktive Verluste im Kondensator usw. Betrachten wir eine reale Schaltung, die aus einem in Reihe geschalteten Kondensator C und einem aktiven Widerstand R besteht (Abb. 14). In diesem Stromkreis fließt ein Strom I = I0 sin ωt.

Gemäß der zweiten Kirchhoff-Regel ist die Summe der Spannungen am Widerstand und am Kondensator gleich der angelegten Spannung:

U = UR + UC (1,41)

Die Spannung am Widerstand ist in Phase mit dem Strom:

UR = U0R sin ωt (1.42)

und die Spannung am Kondensator hinkt dem Strom hinterher:

UC = U0C sin (ωt − π/2) (1.43)

Nachdem wir die Vektoren I, UR und UC konstruiert und Formel (1.41) verwendet haben, ermitteln wir den Vektor U. Das Vektordiagramm für diese Schaltung ist in Abbildung 15 dargestellt.

Wie aus dem Vektordiagramm ersichtlich ist, ist der Modul des Vektors U gleich

U =√ UR + UC =√ I R + I (1/ωC) = I √ R + (1/ωC) = IZ1 (1.44)

Wo ist der Wert?

Z1=√ R + (1/ωC) (1,45)

wird als Impedanz des Stromkreises bezeichnet.

Die Phasenverschiebung φ zwischen Strom und Spannung in einem gegebenen Stromkreis wird ebenfalls aus dem Vektordiagramm bestimmt:

tan φ = UC/ UR = (1/ωC)/ R (1.46)

In der betrachteten Schaltung hängt der Phasenwinkel zwischen Strom und Spannung von den Werten von R und C ab und variiert von 0 bis π/2.

Betrachten wir nun, wie sich die Leistung in einem Stromkreis mit einer aktiv-kapazitiven Last im Laufe der Zeit ändert. Momentane Strom- und Spannungswerte können dargestellt werden als:

U (t) = U0 sin ωt

I (t) = I0 sin (ωt + φ) (1.47)

Dann ist der Momentanleistungswert:

p(t)= I(t) U(t) = I0 U0 sin ωt sin(ωt + φ)=(I0 U0/2) = =(I0 U0/2)(1− cos2ωt) cosφ + (I0 U0/ 2) sin2ωt sinφ (1.48)

Der Momentanleistungswert besteht aus zwei Komponenten: Der erste Term ist aktiv und der zweite ist reaktiv (kapazitiv). Daher ist die durchschnittliche Leistung über den Zeitraum nicht Null:

Pav =1/T ∫ pdt = I0U0/2T cosφ ∫ dt − I0U0/2T cosφ ∫ cos2 ωtdt + I0U0/2T ∙

sin φ ∫ sin2ωt dt = I0U0/2T cosφ (1.49)

und ist die Wirkleistung. Die dieser Leistung entsprechende elektrische Energie wird im Wirkwiderstand R in Wärme umgewandelt.

6. Reihenschaltung bestehend aus aktivem Widerstand, Induktivität und Kapazität

Betrachten Sie nun einen Wechselstromkreis, der eine Induktivität, eine Kapazität und einen Widerstand enthält, die in Reihe geschaltet sind (Abb. 16).

Die an den Stromkreis angelegte Spannung ist gleich der Vektorsumme der Spannungsabfälle an Induktivität, Kapazität und Widerstand:

U = UL + UC + UR (1,50)

Die Spannung am Widerstand ist phasengleich mit dem Strom, die Spannung an der Spule ist dem Strom phasengleich um π/2 voraus und die Spannung am Kondensator liegt phasengleich um π/2 hinter dem Strom. Diese Spannungen können eingeschrieben werden das folgende Formular:

UR = U0R sin ωt = I0R sin ωt

UL = U0Lsin (ωt + π/2) = I0 ωL (ωt + π/2) (1.51)

UC = U0C sin (ωt − π/2) = (I0/ωC) sin (ωt − π/2)

Da wir die Amplituden und Phasen dieser Vektoren kennen, können wir ein Vektordiagramm erstellen und den Vektor U ermitteln (Abb. 17).

Aus dem resultierenden Vektordiagramm können wir den Betrag des Vektors der an den Stromkreis angelegten Spannung U und die Phasenverschiebung φ zwischen Strom und Spannung ermitteln:

U = √ UR + (UL − UC) = I √ R +(ωL− 1/ωC) = IZ (1.52)

Z = √ R +(ωL− 1/ωC) (1.53)

wird als Impedanz des Stromkreises bezeichnet. Das Diagramm zeigt, dass die Phasenverschiebung zwischen Strom und Spannung durch die Gleichung bestimmt wird:

tan φ =(UL − UC)/ UR = (ωL− 1/ωC)/R (1.54)

Als Ergebnis der Diagrammerstellung haben wir ein Spannungsdreieck erhalten, dessen Hypotenuse gleich der angelegten Spannung U ist. In diesem Fall wird die Phasendifferenz zwischen Strom und Spannung durch das Verhältnis der Vektoren UL, UC und bestimmt UR. Wenn UL > UC (Abb. 17), ist der Winkel φ positiv und die Last ist induktiv. Bei UL< UC угол φ отрицателен и нагрузка имеет емкостный характер (рис. 18, а). А при

UL = UC Winkel φ ist Null und die Last ist rein aktiv (Abb. 18, b).

Wenn wir die Seiten des Spannungsdreiecks (Abb. 17) durch den Wert des Stroms im Stromkreis dividieren, erhalten wir ein Widerstandsdreieck (Abb. 19, a), in dem R der aktive Widerstand, Z der Gesamtwiderstand und x = ist xL−xC ─ Reaktanz. Außerdem,

R = Zcosφ; x = Zsinφ (1,55)

Indem wir die Seiten des Spannungsdreiecks mit dem Wert des Stroms im Stromkreis multiplizieren, erhalten wir ein Leistungsdreieck (Abb. 19, b). Dabei ist S die Scheinleistung, Q die Blindleistung und P die Wirkleistung. Aus dem Machtdreieck folgt:

S = IU = √P + Q ; Q = S sin φ ; P = S cos φ = IU cos φ (1,56)

Die Blindleistung Q ist immer mit dem Austausch elektrischer Energie zwischen der Quelle und dem Verbraucher verbunden. Sie wird in Blindvoltampere (Var) gemessen.

Die Gesamtleistung S enthält sowohl aktive als auch reaktive Komponenten – das ist die Leistung, die von der Stromquelle verbraucht wird. Bei P = 0 wird die gesamte Gesamtleistung zur Blindleistung und bei Q = 0 zur Wirkleistung. Daher die Komponenten volle Kraft durch die Art der Belastung bestimmt. Die Scheinleistung wird in Voltampere (VA) gemessen. Dieser Wert ist auf den Etiketten von Wechselstromgeräten angegeben.

Wirkleistung P ist die elektrische Energie, die in andere Energiearten umgewandelt werden kann – Wärme, mechanische Arbeit usw. Sie wird in Watt (W) gemessen. Die Wirkleistung hängt von Strom, Spannung und cos φ ab. Mit zunehmendem Winkel φ nehmen cos φ und Leistung P ab, mit kleiner werdendem Winkel φ steigt die Wirkleistung P. Der cos φ gibt also an, wie viel der Gesamtleistung theoretisch in andere Energiearten umgewandelt werden kann. cos φ wird Leistungsfaktor genannt.

Für mehr rationelle Nutzung Versuchen Sie, die von elektrischen Energiequellen erzeugte Wechselstromleistung so zu gestalten, dass der cos φ im Stromkreis nahe bei eins liegt. In der Praxis ist dies im Unternehmensmaßstab recht schwer zu erreichen guter Indikator ist cos φ =0,9 - 0,95.

Bei niedrige Werte cos φ entstehen zusätzliche Verluste durch Erwärmung des Leiters.

Nehmen wir an, dass gleiche Wirkleistungen bei gleicher Spannung an zwei gleiche Verbraucher mit cos φ0 =1 und cos φ1 übertragen werden<1. Тогда

I0U cos φ0 = I1U cos φ1 (1,57)

I1 = I0 / cos φ1 (1,58)

Die zum Erhitzen der Drähte aufgewendete Leistung ist gleich

P1 = I1 R = I0 R / cos φ1 (1,59)

das heißt, die Wärmeverluste der Drähte sind umgekehrt proportional zum Quadrat des Leistungsfaktors. Das ist so, wie es sein sollte, denn Blindleistung erzeugt zusätzlichen Blindstrom in den Drähten und die Erwärmungsverluste der Drähte sind proportional zum Quadrat des Stroms. Daher ist die Erhöhung des cos φ von großer praktischer Bedeutung.

7. Resonanz von Spannungen und Strömen

Spannungsresonanz

Wenn die um 180° gegeneinander phasenverschobenen Spannungen an der Induktivität und Kapazität UL und UC gleich groß sind, kompensieren sie sich vollständig (Abb. 18, b). Die an den Stromkreis angelegte Spannung ist gleich der Spannung am aktiven Widerstand, und der Strom im Stromkreis ist in Phase mit der Spannung. Dieser Fall wird als Spannungsresonanz bezeichnet.

Voraussetzung für Spannungsresonanz ist die Gleichheit der Spannungen an Induktivität und Kapazität bzw. die Gleichheit der induktiven und kapazitiven Reaktanzen des Stromkreises:

xL = xC oder ωL = 1/ωC ​​​​(1,60)

Bei Spannungsresonanz ist der Strom im Stromkreis gleich

I = U/√R + 0 = U/R (1.61)

das heißt, der Stromkreis hat in diesem Fall den geringstmöglichen Widerstand, als ob nur der aktive Widerstand R darin enthalten wäre. Der Strom im Stromkreis erreicht seinen Maximalwert.

Bei Resonanz können die Spannungen an den Reaktanzen xL und xC die an den Stromkreis angelegte Spannung deutlich übersteigen. Wenn wir das Verhältnis der angelegten Spannung zur Spannung an der Induktivität (oder Kapazität) nehmen, erhalten wir:

U/ UL = IZ/I xL = Z/ xL oder UL = U xL /R (1,62)

Das heißt, die Spannung an der Induktivität ist xL/R-mal größer als die angelegte Spannung. Dies bedeutet, dass beim Auftreten von Spannungsresonanzen in einzelnen Abschnitten des Stromkreises Spannungen entstehen können, die gefährlich für die Isolierung der in diesem Stromkreis enthaltenen Geräte sind. Das Vektordiagramm für den Fall der Spannungsresonanz ist in Abb. dargestellt. 18 v.

Wenn sich in einer Reihenschaltung aus aktivem Widerstand, Induktivität und Kapazität der Wert eines der Schaltungselemente (z. B. der Kapazität) bei konstanter angelegter Spannung ändert, ändern sich viele Werte, die den Strom im Stromkreis charakterisieren. Kurven, die zeigen, wie sich Strom und Spannung ändern, werden als resonant bezeichnet. Resonanzkurven mit Kapazitätsänderungen sind in Abbildung 20 dargestellt.

Aktuelle Resonanz

Im Gegensatz zu Reihenwechselstromkreisen, bei denen der durch alle Elemente des Stromkreises fließende Strom gleich ist, ist in Parallelschaltungen die an die parallel geschalteten Zweige des Stromkreises angelegte Spannung gleich.

Betrachten wir die Parallelschaltung einer Kapazität und eines Zweigs bestehend aus Induktivität und aktivem Widerstand (Abb. 21).

Beide Zweige liegen unter der gleichen angelegten Spannung U. Erstellen wir ein Vektordiagramm für diese Schaltung. Als Hauptvektor wählen wir den Vektor der angelegten Spannung U (Abb. 22).

Dann ermitteln wir die Länge des Vektors I1 aus der Beziehung

I1 = U/z1 = U/√R1 + xL (1.63)

und stellen Sie diesen Vektor in Bezug auf den Vektor U in einem Winkel φ1 beiseite, der durch die Formel bestimmt wird

tan φ1 = xL/ R1 (1,64)

Der so erhaltene Stromvektor I1 wird in zwei Komponenten zerlegt: Wirkstrom Ia1 = I1 cos φ1 und Blindstrom Ip1 = I1 sin φ1 (Abb. 22).

Der Betrag des Stromvektors I2 ergibt sich aus der Beziehung

I2 = U/ xC = U/(1/ωC) = ωCU (1,65)

und stellen Sie diesen Vektor in einem Winkel von 90 gegen den Uhrzeigersinn relativ zum Vektor der angelegten Spannung U ein.

Der Gesamtstrom I ist gleich der geometrischen Summe der Ströme I1 und I2 oder der geometrischen Summe des Blindstroms Ip1 - I2 =IL - IC und des Wirkstroms Ia1. die Länge des Vektors I ist

I = √(IL − IC) ​​​​+(Ia1) (1.66)

Aus der Beziehung lässt sich die Phasenverschiebung zwischen dem Gesamtstrom I und der angelegten Spannung U ermitteln

tanφ =(IL − IC)/ Ia1 (1,67)

Aus dem Zeigerdiagramm ist ersichtlich, dass Länge und Lage des Gesamtstromvektors vom Verhältnis der Blindströme IL und IC abhängen. Insbesondere wenn IL > IC, ist der Gesamtstrom phasenverschoben zur angelegten Spannung, wenn IL< IC ─ опережает его, а при IL = IC ─ совпадает с ним по фазе. Последний случай (IL = IC) называется резонансом токов. При резонансе токов общий ток равен активной составляющей тока в цепи, то есть происходящие в цепи процессы таковы, как будто в ней содержится только активное сопротивление (в этом случае φ = 0 и cos φ = 1). При резонансе общий ток в цепи принимает минимальное значение и становится чисто активным, тогда как Blindströme in den Zweigen ungleich Null und gegenphasig sind.

Wenn in der in Abbildung 21 gezeigten Parallelschaltung der Kapazitätswert bei konstanter angelegter Spannung geändert wird, ändern sich viele Größen, die den Strom in der Schaltung charakterisieren. Kurven, die zeigen, wie sich Strom, Spannung in Abschnitten eines Stromkreises und die Phasenverschiebung zwischen Strom und Spannung ändern, werden als resonant bezeichnet.

Elektrische Energie wird fast immer in Form von Wechselstromenergie erzeugt, verteilt und verbraucht.

Breite Anwendung von Wechselstrom in Diverse Orte Die Technologie erklärt sich aus der einfachen Herstellung und Umwandlung sowie der einfachen Konstruktion von Generatoren und Wechselstrommotoren, der Zuverlässigkeit ihres Betriebs und der einfachen Bedienung.

Wechselstrom ändert seinen Wert und seine Richtung, bestimmte Nummer einmal pro Sekunde. Bei Wechselstrom bewegen sich Elektronen entlang des Drahtes zunächst in eine Richtung, bleiben dann für einen Moment stehen, bewegen sich dann in die entgegengesetzte Richtung, halten wieder an und wiederholen die Bewegung hin und her. Das heißt, Elektronen führen im Draht eine oszillierende Bewegung aus. Aufgrund ihrer geringen Bewegungsgeschwindigkeit (V el = 10 -4 m/s = 0,1 mm/s) haben Elektronen bei solchen Schwingungen Zeit, nur kleine Bewegungen entlang des Drahtes auszuführen.

Am gebräuchlichsten ist der sogenannte sinusförmige Wechselstrom. Die zeitliche Änderung elektrischer Größen (Strom, Spannung, EMK) wird durch eine glatte gekrümmte Linie, die sogenannte Sinuswelle, dargestellt.

Stromkreise, in denen sich die Werte und Richtungen von EMK, Spannung und Strom im Laufe der Zeit nach einem Sinusgesetz periodisch ändern, werden Stromkreise genannt sinusförmiger Strom. Manchmal werden sie auch einfach Wechselstromkreise genannt.

Für Wechselstrom wurde die Sinuswellenform gewählt, da sie eine wirtschaftlichere Erzeugung, Übertragung, Verteilung und Nutzung elektrischer Energie ermöglicht.

Darüber hinaus bleibt die Sinusform elektrischer Größen in allen Abschnitten eines beliebig komplexen Stromkreises, also induktiv und, unverändert kapazitive Elemente, in Stromkreisen enthalten, verändern die Sinusform von Strom und Spannung nicht.

Wechselstromkreise weisen im Vergleich zu Gleichstromkreisen eine Reihe von Merkmalen auf. Diese Merkmale werden bestimmt durch:

Erstens dadurch, dass Wechselstromkreise neue Elemente enthalten: Transformatoren, Kondensatoren, Induktivitäten;

zweitens dadurch, dass Wechselströme und -spannungen in diesen Elementen elektrische und magnetische Wechselfelder erzeugen, die wiederum zur Entstehung des Phänomens der Selbstinduktion, der Gegeninduktion und der Verschiebungsströme führen.

All dies hat erhebliche Auswirkungen auf die im Stromkreis ablaufenden Prozesse. Die Analyse von Vorgängen in Schaltkreisen wird komplizierter.

Für einen sinusförmigen Wechselstromkreis sehr wichtig hat eine Frequenz F. Der Einfluss von Kapazitäten und Induktivitäten auf Vorgänge im Stromkreis ist frequenzabhängig.

Merkmale sinusförmiger Stromkreise verursachen eine Reihe neuer Phänomene, die für diese Kreise spezifisch sind: Phasenverschiebung, Resonanzphänomen und das Auftreten von Blindleistungen.

Leistungsfaktor.

In modernen Industriebetrieben sind die meisten Verbraucher von elektrischer Wechselstromenergie aktiv-induktive Lasten in Form von asynchronen Elektromotoren, Leistungstransformatoren, Schweißtransformatoren, Umrichtern usw. In einer solchen Last wird durch den Wechselstromfluss eine Selbstinduktions-EMK induziert, die eine Phasenverschiebung zwischen Strom und Spannung verursacht. Diese Phasenverschiebung nimmt normalerweise zu cos  nimmt bei geringer Belastung ab. Zum Beispiel, wenn cos  Bei Wechselstrommotoren liegt der Wert bei Volllast bei 0,75 bis 0,8, bei geringer Last sinkt er dann auf 0,2 bis 0,4.

Wenn die von allen Empfängern in diesen Stromkreisen verbrauchte Leistung ziemlich genau ist, beträgt ihr Strom bei konstanter Spannung an den Empfängeranschlüssen: ICH = P / (U cos  )

Mit abnehmender cos  Der Laststrom von Kraftwerken und Umspannwerken erhöht sich bei gleicher Ausgangsleistung.

Elektrische Generatoren, Transformatoren und Stromleitungen sind jedoch für eine bestimmte Spannung und einen bestimmten Strom ausgelegt. Anstieg des Verbraucherstroms beim Absinken cos bestimmte Grenzwerte nicht überschreiten, da die sie versorgenden Generatoren für eine bestimmte Nennleistung ausgelegt sind S nom = U nom  ICH nom Daher sollten sie nicht überlastet werden. Um sicherzustellen, dass der Generatorstrom beim Absinken den Nennwert nicht überschreitet cos  Verbraucher muss dessen Wirkleistung reduziert werden. Also das Downgrade cos  Verbraucher entstehen durch unvollständige Nutzung der Leistung von Synchrongeneratoren, Transformatoren und Stromleitungen. Sie werden durch induktiven Blindstrom nutzlos belastet.

cos , der die Nutzung der installierten Leistung charakterisiert, wird oft als Leistungsfaktor bezeichnet.

Der Leistungsfaktor ist als Verhältnis definiert Wirkleistung zu voll:

cos = P/S.

Der Leistungsfaktor (2,25) gibt an, welcher Teil der elektrischen Energie irreversibel in andere Energiearten umgewandelt und insbesondere zur Verrichtung nützlicher Arbeit genutzt wird. Gilt als normal cos 0,85 - 0,9. Ist der Leistungsfaktor niedrig, werden die Unternehmen, die Strom verbrauchen, mit einer Geldstrafe belegt, ist der Leistungsfaktor hoch, erhalten die Unternehmen Prämien.

Um den Leistungsfaktor zu verbessern, werden verschiedene Maßnahmen ergriffen:

2. Wechselstrommotoren, die relativ gering belastet sind, werden durch Motoren mit geringerer Leistung ersetzt;

2. Kondensatoren sind parallel zu den Empfängern geschaltet.

Die unten angegebenen theoretischen Informationen können bei der Vorbereitung auf die Laborarbeiten 6, 7, 8 im Labor für Elektrizität und Magnetismus hilfreich sein. Für eine detailliertere Untersuchung empfehlen wir das Lehrbuch „Elektrizität“ (Moskau, „Wissenschaft“ – 1985) von S. G. Kalaschnikow, auf dessen Grundlage dieses Lehrhandbuch zusammengestellt wurde.

Betrachten wir die elektrischen Schwingungen, die auftreten, wenn sich ein Generator im Stromkreis befindet. elektromotorische Kraft die sich periodisch ändert. Darüber hinaus beschränken wir uns auf die Untersuchung elektrischer Schaltkreise mit konzentrierten Kapazitäten und Induktivitäten und betrachten Wechselströme als quasistationär. Quasistationarität bedeutet das sofortig aktuelle Werte ich in allen Abschnitten der Folgeschaltung nahezu identisch. Diese Bedingung ist erfüllt, wenn beim Durchgang des Signals durch den Stromkreis ( 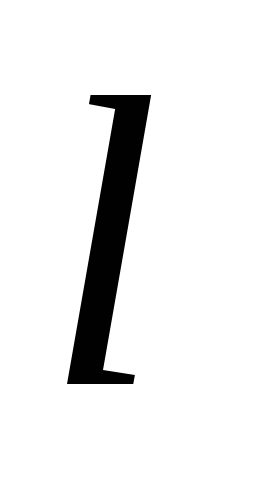- Kettenlänge, C- Lichtgeschwindigkeit) ändert sich die Stromstärke geringfügig (

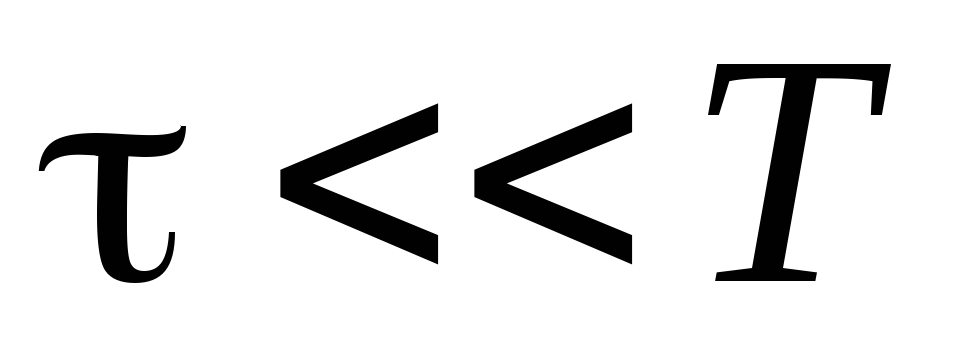, Wo T- Schwingungsdauer). Wenn wir akzeptieren l= 1 m, dann können die Ströme bei Frequenzen als quasistationär angesehen werden

300 MHz.

Wir betrachten nur solche Ströme, die sich nach einem Sinusgesetz ändern. Dies hat mehrere Gründe. Erstens haben viele technische Wechselstromgeneratoren eine EMK, die sich nach einem nahezu sinusförmigen Gesetz ändert, und daher sind die von ihnen erzeugten Ströme praktisch sinusförmig. Zweitens ist die Theorie sinusförmiger Ströme besonders einfach und daher lassen sich am Beispiel solcher Ströme die Grundzüge elektrischer Schwingungen leicht verdeutlichen. Drittens ist nach dem bekannten mathematischen Theorem von Fourier jede Funktion

genug Gesamtansicht kann als Summe von Sinusfunktionen dargestellt werden. Daher ermöglicht die Theorie des Sinusstroms, wichtige Ergebnisse für einen Strom zu erhalten, der sich im Laufe der Zeit nach einem willkürlichen (nicht sinusförmigen) Gesetz ändert.

Wo dies nicht ausdrücklich vermerkt ist, gehen wir abschließend davon aus, dass die Schwingungen stetig sind. Mit anderen Worten, wir gehen davon aus, dass seit Beginn der Schwingungen eine ausreichend lange Zeit vergangen ist, so dass Amplituden Strom und Spannung haben bereits ihre konstanten Werte erreicht und ändern sich nicht weiter.

Widerstand im Wechselstromkreis

Lassen Sie uns zunächst überlegen besonderer Fall, wenn der Wechselstromgenerator an einen externen Stromkreis angeschlossen ist, dessen Induktivität und Kapazität so gering sind, dass sie vernachlässigt werden können. Angenommen, im Stromkreis fließt Wechselstrom

,

(ich- momentaner Stromwert, - aktuelle Amplitude, - zyklische Frequenz) und finden Sie heraus, nach welchem ​​Gesetz sich die Spannung zwischen den Enden des Stromkreises ändert A Und B (Abb. 1). Bewerben in der Gegend ARb Wir verstehen das Ohmsche Gesetz

.

Somit ist die Spannung an den Enden des Schaltungsabschnitts nach dem Kosinusgesetz auch von der Zeit abhängig, und die Phasendifferenz zwischen Strom- und Spannungsschwingungen ist Null (ihre Schwingungen erfolgen gleichphasig): Spannung und Strom erreichen gleichzeitig Maximalwerte ​​und gleichzeitig auf Null stellen (Abb. 2) . Der maximale Spannungswert beträgt

.

Betrachten wir nun, wie groß die im Schaltkreis geleistete Arbeit ist. Für einen kurzen Zeitraum kann Wechselstrom als Gleichstrom betrachtet werden, und daher beträgt die Momentanleistung des Wechselstroms

Abb. 3. Abhängigkeiten von Strom durch einen Widerstand, Spannung und Momentanleistung von der Zeit

Die zeitliche Änderung der Momentanleistung ist in Abb. 3 dargestellt. Auch die aktuellen Schwingungskurven sind hier angegeben. ich und Spannung u. Normalerweise ist es nicht erforderlich, den Momentanwert der Leistung zu kennen, sondern ihren Durchschnittswert über einen langen Zeitraum, der viele Schwingungsperioden abdeckt. Da es sich um einen periodischen Prozess handelt, reicht es zur Ermittlung dieses Durchschnittswerts natürlich aus, den durchschnittlichen Leistungswert für eine vollständige Periode zu berechnen. Wechselstrombetrieb in kurzer Zeit dt Es gibt

,

und daher arbeiten A während der gesamten Schwingungsdauer T ausgedrückt durch die Formel

.

.

Deshalb

. Von hier aus für mittlere Leistung wir bekommen

.

Als

, dann können wir auch schreiben

.

Bezeichnen wir mit

Und

Strom und Spannung des Gleichstroms, der im Widerstand abgegeben wird R die gleiche Wärmemenge wie ein gegebener Wechselstrom. Dann

.

Wenn wir diese Ausdrücke mit den Ausdrücken für Wechselstrom vergleichen, haben wir Folgendes:

.

Größe

wird als effektiver (oder effektiver) Wert des Wechselstroms bezeichnet und

- effektiver Spannungswert. Mithilfe effektiver Werte können Sie die durchschnittliche Wechselstromleistung mithilfe derselben Formeln wie die Gleichstromleistung ausdrücken.