Active resistance, inductance and capacitance in an alternating current circuit.

Changes in current, voltage, etc. d.s. in an alternating current circuit occur with the same frequency, but the phases of these changes are, generally speaking, different. Therefore, if the initial phase of the current is conventionally taken as zero, then the initial phase of the voltage will have a certain value φ. Under this condition, the instantaneous values ​​of current and voltage will be expressed by the following formulas:

i = I m sinωt

u = U m sin(ωt + φ)

a) Active resistance in an alternating current circuit. Circuit resistance, which causes irretrievable losses of electrical energy to thermal effect of current, called active . This resistance for low frequency current can be considered equal to the resistance R the same conductor to direct current.

In an alternating current circuit that has only active resistance, for example, in incandescent lamps, heating devices etc., the phase shift between voltage and current is zero, i.e. φ = 0. This means that the current and voltage in such a circuit change in the same phases, and the electrical energy is completely spent on the thermal effect of the current.

We will assume that the voltage at the circuit terminals changes according to a harmonic law: And = U t cos ωt.

As in the case direct current, the instantaneous current value is directly proportional to the instantaneous voltage value. Therefore, to find the instantaneous current value, you can apply Ohm’s law:

in phase with voltage fluctuations.

b) Inductor in an alternating current circuit. Connecting an inductance coil to an alternating current circuit L manifests itself as an increase in circuit resistance. This is explained by the fact that with alternating current the e is always active in the coil. d.s. self-induction, weakening the current. Resistance XL, which is caused by the phenomenon of self-induction is called inductive reactance. Since e. d.s. self-inductance is greater, the greater the inductance of the circuit and the faster the current changes, then the inductive reactance is directly proportional to the inductance of the circuit L and circular frequency of alternating current ω: XL = ωL .

Let us determine the current strength in a circuit containing a coil whose active resistance can be neglected. To do this, we first find the connection between the voltage on the coil and Self-induced emf in it. If the coil resistance is zero, then the voltage electric field inside the conductor at any time must be equal to zero. Otherwise, the current strength, according to Ohm's law, would be infinitely large.

The equality of the field strength to zero is possible because the strength of the vortex electric field Ei, generated by an alternating magnetic field, at each point is equal in magnitude and opposite in direction to the intensity of the Coulomb field E k, created in the conductor by charges located at the terminals of the source and in the wires of the circuit.

From equality E i = -E k follows that specific work of the vortex field(i.e. self-induced emf e i) is equal in magnitude and opposite in sign to the specific work of the Coulomb field. Considering that the specific work of the Coulomb field is equal to the voltage at the ends of the coil, we can write: e i = -i.

When the current changes according to the harmonic law i = I m sin сosωt, self-induction emf is equal to: e i = -Li"= -LωI m cos ωt. Because e i = -and, then the voltage at the ends of the coil turns out to be equal

And= LωI m cos ωt = LωI m sin (ωt + π/2) = U m sin (ωt + π/2)

whereU m = LωI m - voltage amplitude.

Consequently, the voltage fluctuations on the coil are ahead of the current fluctuations in phase by π/2, or, what is the same, current fluctuations are out of phase with voltage fluctuations byπ/2.

If you enter the designation XL = ωL, then we get . Size X L, equal to the product of the cyclic frequency and inductance, is called inductive reactance. According to the formula , the current value is related to the voltage value and inductive reactance by a relationship similar to Ohm's law for a direct current circuit.

Inductive reactance depends on frequency ω. Direct current does not “notice” the inductance of the coil at all. At ω = 0, the inductive reactance is zero. The faster the voltage changes, the greater the self-induction EMF and the smaller the amplitude of the current. It should be noted that the voltage across the inductive reactance is ahead of the current in phase.

c) Capacitor in an alternating current circuit. Direct current does not pass through the capacitor, since there is a dielectric between its plates. If a capacitor is connected to a DC circuit, then after charging the capacitor, the current in the circuit will stop.

Let the capacitor be connected to an alternating current circuit. Capacitor charge (q=CU) due to changes in voltage, it changes continuously, so there is flow in the circuit alternating current. The greater the capacitance of the capacitor and the more often it is recharged, i.e., the greater the frequency of the alternating current, the greater the current strength.

The resistance caused by the presence of electrical capacitance in an alternating current circuit is called capacitive reactance X s. It is inversely proportional to capacitance WITH and circular frequency ω: Х с =1/ωС.

Let us establish how the current strength changes over time in a circuit containing only a capacitor, if the resistance of the wires and plates of the capacitor can be neglected.

The voltage across the capacitor u = q/C is equal to the voltage at the ends of the circuit u = U m cosωt.

Therefore, q/C = U m cosωt. The charge of the capacitor changes according to the harmonic law:

q = CU m cosωt.

The current strength, which is the time derivative of the charge, is equal to:

i = q" = -U m Cω sin ωt =U m ωC cos(ωt + π/2).

Hence, current fluctuations are ahead in phase of voltage fluctuations on the capacitor byπ/2.

Size X s, the reciprocal of the product ωС of the cyclic frequency by electrical capacitance capacitor is called capacitance. The role of this quantity is similar to the role of active resistance R in Ohm's law. The value of the current is related to the value of the voltage on the capacitor in the same way as the current and voltage are related according to Ohm's law for a section of a DC circuit. This allows us to consider the value X s as the resistance of a capacitor to alternating current (capacitance).

The larger the capacitor capacity, the more current recharge. This is easy to detect by the increase in the lamp's incandescence as the capacitor's capacitance increases. While a capacitor's resistance to direct current is infinite, its resistance to alternating current is finite. X s. As capacity increases, it decreases. It also decreases with increasing frequency ω.

In conclusion, we note that during the quarter period when the capacitor is charged to its maximum voltage, energy enters the circuit and is stored in the capacitor in the form of electric field energy. In the next quarter of the period, when the capacitor is discharged, this energy is returned to the network.

From a comparison of formulas XL = ωL And Х с =1/ωС It can be seen that the inductors are. represent a very large resistance for high-frequency current and a small one for low-frequency current, and capacitors do the opposite. Inductive X L and capacitive X C resistances are called reactive.

d) Ohm's law for electrical circuit alternating current.

Let us now consider the more general case of an electrical circuit in which a conductor with active resistance is connected in series R and low inductance, coil with high inductance L and low active resistance and a capacitor with a capacity WITH

We have seen that when connected individually to an active resistance circuit R, capacitor with a capacity WITH or coils with inductance L The amplitude of the current is determined accordingly by the formulas:

; ; I m = U m ωC.

The voltage amplitudes on the active resistance, inductor and capacitor are related to the amplitude of the current as follows: U m = I m R; U m = I m ωL;

In DC circuits, the voltage at the ends of the circuit is equal to the sum of the voltages at individual series-connected sections of the circuit. However, if you measure the resulting voltage on the circuit and the voltage on individual elements circuit, it turns out that the voltage on the circuit (rms value) is not equal to the sum of the voltages on the individual elements. Why is this so? The fact is that harmonic voltage fluctuations on various areas the circuits are out of phase with each other.

Indeed, the current at any time is the same in all sections of the circuit. This means that the amplitudes and phases of currents flowing through areas with capacitive, inductive and active resistance are the same. However, only at active resistance are the voltage and current oscillations in phase. On a capacitor, voltage fluctuations lag in phase behind current fluctuations by π/2, and on an inductor, voltage fluctuations lead current fluctuations by π/2. If we take into account the phase shift between the added voltages, it turns out that

To obtain this equality, you need to be able to add voltage oscillations that are out of phase relative to each other. The easiest way to perform the addition of several harmonic oscillations is using vector diagrams. The idea of ​​the method is based on two fairly simple principles.

Firstly, the projection of a vector with modulus x m rotating at a constant angular velocity performs harmonic oscillations: x = x m cosωt

Secondly, when adding two vectors, the projection of the total vector is equal to the sum of the projections of the added vectors.

A vector diagram of electrical oscillations in the circuit shown in the figure will allow us to obtain the relationship between the amplitude of the current in this circuit and the amplitude of the voltage. Since the current strength is the same in all sections of the circuit, it is convenient to start constructing a vector diagram with the current vector I m. We will depict this vector as a horizontal arrow. The voltage across the active resistance is in phase with the current. Therefore the vector UmR, must coincide in direction with the vector I m. Its modulus is UmR = ImR

Voltage fluctuations across the inductive reactance are ahead of current fluctuations by π/2, and the corresponding vector U m L must be rotated relative to the vector I m by π/2. Its modulus is U m L = I m ωL. If we assume that a positive phase shift corresponds to a counterclockwise rotation of the vector, then the vector U m L you should turn left. (One could, of course, do the opposite.)

Its modulus is UmC =I m /ωC. To find the vector of the total voltage U m you need to add three vectors: 1) U mR 2) U m L 3) U mC

First, it is more convenient to add two vectors: U m L and U m C

The modulus of this sum is equal to , if ωL > 1/ωС. This is exactly the case shown in the figure. After this, adding the vector ( U m L + U m C) with vector UmR we get a vector U m, depicting voltage fluctuations in the network. According to the Pythagorean theorem:

From the last equality you can easily find the amplitude of the current in the circuit:

Thus, due to the phase shift between the voltages in different parts of the circuit, the total resistance Z the circuit shown in the figure is expressed as follows:

From the amplitudes of current and voltage, we can move on to the effective values ​​of these quantities:

This is Ohm's law for alternating current in the circuit shown in Figure 43. The instantaneous value of the current changes harmoniously with time:

i = I m cos (ωt+ φ), where φ is the phase difference between the current and voltage in the network. It depends on the frequency ω and circuit parameters R, L, S.

e) Resonance in an electrical circuit. While studying forced mechanical vibrations, we became acquainted with an important phenomenon - resonance. Resonance is observed when the natural frequency of oscillations of the system coincides with the frequency of the external force. At low friction there is a sharp increase in the amplitude of steady-state forced oscillations. The coincidence of the laws of mechanical and electromagnetic oscillations immediately allows one to draw a conclusion about the possibility of resonance in an electrical circuit, if this circuit is an oscillatory circuit with a certain natural frequency of oscillations.

The amplitude of the current during forced oscillations in the circuit, occurring under the influence of an external harmonically varying voltage, is determined by the formula:

At a fixed voltage and given values ​​of R, L and C , the current reaches its maximum at a frequency ω that satisfies the relation

This amplitude is especially large at low R. From this equation, you can determine the value of the cyclic frequency of alternating current at which the current is maximum:

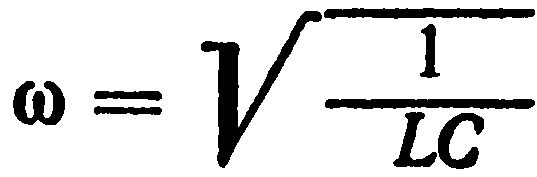
This frequency coincides with the frequency of free oscillations in a circuit with low active resistance.

A sharp increase in the amplitude of forced current oscillations in an oscillatory circuit with low active resistance occurs when the frequency of the external alternating voltage coincides with the natural frequency of the oscillatory circuit. This is the phenomenon of resonance in an electric oscillatory circuit.

Simultaneously with the increase in current strength at resonance, the voltages on the capacitor and inductor increase sharply. These stresses become identical and are many times greater than the external stress.

Really,

U m, C, res =

U m, L,res =

The external voltage is related to the resonant current as follows:

U m = . If That U m , C ,res = U m , L ,res >> U m

At resonance, the phase shift between current and voltage becomes zero.

Indeed, voltage fluctuations across the inductor and capacitor always occur in antiphase. The resonant amplitudes of these voltages are the same. As a result, the voltage on the coil and capacitor is completely compensated each other, and the voltage drop occurs only across the active resistance.

The zero phase shift between voltage and current at resonance ensures optimal conditions to receive energy from the source AC voltage into the chain. There is a complete analogy with mechanical vibrations: at resonance, the external force (analogous to voltage in a circuit) is in phase with the speed (analogous to current).

Resistance in AC circuit

Electric current in conductors is continuously associated with magnetic and electric fields. Elements that characterize the conversion of electromagnetic energy into heat are called active resistances (denoted R). Typical representatives active resistances are resistors, incandescent lamps, electric ovens etc.

Inductive reactance. Formula of inductive reactance.

Elements associated with availability only magnetic field, are called inductances. Coils, windings and etc. have inductance. Inductive reactance formula:

where L is inductance.

Capacitance. Capacitance formula.

Elements associated with the presence of an electric field are called capacitances. Capacitors, long power lines, etc. have capacitance. Capacitance formula:

where C is capacity.

Total resistance. Total resistance formulas.

Real consumers electrical energy resistance may also have a complex meaning. In the presence of active R and inductive L resistances, the value of the total resistance Z is calculated using the formula:

Similarly, the total resistance Z is calculated for the circuit of active R and capacitive resistance C.

Let us now assume that a section of the circuit contains a capacitor C, and the resistance and inductance of the section can be neglected, and let’s see according to what law the voltage at the ends of the section will change in this case. Let us denote the voltage between points A And b through u and we will calculate the charge of the capacitor q and current strength i positive if they correspond to Fig. 4. Then

and therefore

If the current in a circuit changes according to the law

then the charge of the capacitor is equal to

.

Constant of integration q 0 here denotes an arbitrary constant charge of the capacitor, not associated with current fluctuations, and therefore we will put . Hence,

. (2)

Comparing (1) and (2), we see that with sinusoidal current oscillations in the circuit, the voltage on the capacitor also changes according to the cosine law. However, the voltage fluctuations across the capacitor are out of phase with the current fluctuations by p/2. Changes in current and voltage over time are shown graphically in Fig. 5. The result obtained has a simple physical meaning. The voltage across a capacitor at any given time is determined by the existing charge on the capacitor. But this charge was formed by a current that had previously flowed in an earlier stage of oscillation. Therefore, voltage fluctuations lag behind current fluctuations.

Formula (2) shows that the voltage amplitude across the capacitor is equal to

Comparing this expression with Ohm's law for a section of a circuit with direct current (), we see that the quantity

plays the role of resistance of a section of the circuit, it is called capacitance. Capacitance depends on frequency w, and at high frequencies even small capacitances can present very little resistance to alternating current. It is important to note that capacitance determines the relationship between amplitude, and not instantaneous, current and voltage values.

Instantaneous power alternating current

changes over time according to a sinusoidal law with double the frequency. During the time from 0 to T/4 power is positive, and in the next quarter of the period the current and voltage have opposite signs and the power becomes negative. Since the average value over the period of oscillation of a quantity is zero, then average power AC on the capacitor.

Capacitors, like resistors, are among the most numerous elements of radio engineering devices. The main property of capacitors is ability to accumulate electrical charge . The main parameter of a capacitor is its capacity .

The larger the area of ​​its plates and the thinner the dielectric layer between them, the greater the capacitance of the capacitor. The basic unit of electrical capacitance is the farad (abbreviated F), named after the English physicist M. Faraday. However, 1 F is a very large capacity. The globe, for example, has a capacity of less than 1 F. In electrical and radio engineering, a unit of capacity equal to a millionth of a farad is used, which is called microfarad (abbreviated uF) .

The capacitance of a capacitor to alternating current depends on its capacitance and current frequency: the greater the capacitance of the capacitor and the frequency of the current, the lower its capacitance.

Ceramic capacitors have relatively small capacitances - up to several thousand picofarads. They are placed in those circuits in which high-frequency current flows (antenna circuit, oscillatory circuit) for communication between them.

The simplest capacitor consists of two conductors electric current, for example: - two metal plates, called capacitor plates, separated by a dielectric, for example: - air or paper. The larger the area of ​​the capacitor plates and the closer they are located to each other, the greater the electrical capacitance of this device. If a direct current source is connected to the capacitor plates, a short-term current will arise in the resulting circuit and the capacitor will be charged to a voltage equal to the voltage of the current source. You may ask: why does current occur in a circuit where there is a dielectric? When we connect a current source to a capacitor, the electrons in the conductors of the resulting circuit begin to move towards the positive pole of the current source, forming a short-term flow of electrons throughout the circuit. As a result, the plate of the capacitor, which is connected to the positive pole of the current source, is depleted of free electrons and is charged positively, and the other plate is enriched in free electrons and, therefore, is charged negatively. Once the capacitor is charged, the short-term current in the circuit, called the capacitor charging current, will stop.

If the current source is disconnected from the capacitor, the capacitor will be charged. The dielectric prevents the transfer of excess electrons from one plate to another. There will be no current between the plates of the capacitor, and the electrical energy accumulated by it will be concentrated in electric field dielectric. But as soon as the plates of a charged capacitor are connected with some kind of conductor, the “excess” electrons of the negatively charged plate will pass through this conductor to another plate where they are missing, and the capacitor will be discharged. In this case, a short-term current also arises in the resulting circuit, called the capacitor discharge current. If the capacity of the capacitor is large and it is charged to a significant voltage, the moment it is discharged is accompanied by the appearance of a significant spark and crackling sound. The property of a capacitor to accumulate electrical charges and discharge through conductors connected to it is used in the oscillatory circuit of a radio receiver.

Capacitor(from lat. condensare- “compact”, “thicken”) - a two-terminal network with a certain capacitance value and low conductivity; a device for accumulating charge and energy of an electric field. A capacitor is a passive electronic component. In its simplest form, the design consists of two plate-shaped electrodes (called linings), separated by a dielectric whose thickness is small compared to the dimensions of the plates (see figure). Practically used capacitors have many layers of dielectric and multilayer electrodes, or strips of alternating dielectric and electrodes, rolled into a cylinder or parallelepiped with four rounded edges (due to winding). A capacitor in a DC circuit can conduct current at the moment it is connected to the circuit (charging or recharging of the capacitor occurs); at the end of the transient process, no current flows through the capacitor, since its plates are separated by a dielectric. In an alternating current circuit, it conducts alternating current oscillations through cyclic recharging of the capacitor, closing with the so-called bias current.

From the point of view of the complex amplitude method, the capacitor has a complex impedance

,

Where j - imaginary unit, ω - cyclic frequency ( rad/s) flowing sinusoidal current, f - frequency in Hz, C - capacitor capacity ( farad). It also follows that the reactance of the capacitor is equal to: . For direct current, the frequency is zero, therefore the reactance of the capacitor is infinite (ideally).

The resonant frequency of the capacitor is

At f > f p A capacitor in an AC circuit behaves like an inductor. Therefore, it is advisable to use a capacitor only at frequencies f< f p , where its resistance is capacitive in nature. Typically, the maximum operating frequency of a capacitor is approximately 2-3 times lower than the resonant frequency.

A capacitor can store electrical energy. Energy of a charged capacitor:

Where U - voltage (potential difference) to which the capacitor is charged.