The capacitor is discharged through the resistor. Investigation of the Discharging Process of a Capacitor
Charging and discharging a capacitor
1 Charge dielectric capacitor
The fallacy of the existing interpretation of the operation of a capacitor is especially obvious. It is based on the presence of positive and negative charges in the electrical circuit. The carriers of these charges are known: the proton and the electron. However, they are also known to sense each other's presence a thousand times over. larger an electron and a million times the size of a proton. Even such a distant proximity of them ends with the formation of hydrogen atoms, which exist only in the plasma state at temperatures up to 5000 C. This occurs, for example, in the processes of removal of electrons and protons from the Sun and their subsequent combination into hydrogen atoms. So the joint presence of protons and electrons in a free state in conductors is completely excluded, therefore, the positive and negative potentials on the plates of a dielectric capacitor are a mistake of physicists. Let's fix it.
Now we will see that the plates of a dielectric capacitor are charged not with opposite electrical polarity, but with opposite magnetic polarity. In this case, the plus functions belong to the south magnetic pole of the electron, and the minus functions belong to the north. These poles form the polarity, but not electrical, but magnetic. Let us follow the process of charging a dielectric capacitor to see how the magnetic poles of an electron form the magnetic polarity of its plates. It is known that between the plates of a dielectric capacitor there is a dielectric D (Fig. 1, a).
The scheme of the experiment on charging a dielectric capacitor is shown in fig. 1, a. The most important requirement for the scheme is its orientation from south (S) to north (N). To ensure complete isolation of the capacitor from the network after it has been charged, it is advisable to use electrical plug plugged into a 220 V mains socket.
Immediately after the diode, compass 1 (K) is shown, placed on the wire going to the capacitor C. The arrow of this compass, deviating to the right at the moment the plug is turned on, shows the direction of electron movement (Fig. 1) from the point S to the bottom plate of the capacitor. Here it is appropriate to pay attention to the generality of information about the behavior of electrons in wires, presented in Fig. 1.
Rice. 1. Scheme of our capacitor charging experiment
Above compass 1 (Fig. 1) shows a diagram of the direction magnetic field around a wire formed by electrons moving in it.
Thus, the electrons passing through the diode arrive at the bottom plate of the capacitor with oriented spin vectors
and magnetic moments to its inner surface(Fig. 1). As a result, the northern magnetic potential (N) is formed on this surface.It is quite natural that electrons will come to the inner surface of the upper plate of the capacitor from the network, oriented by the south magnetic poles (S). The proof of this is the experimental fact of the deviation of the needle of the upper compass 2 (K) to the right (Fig. 1). This means that the electrons moving from the network to the upper plate of the capacitor are oriented by the south magnetic poles (S) in the direction of movement (Fig. 2).
Thus, the orientation of electrons on the plates of a dielectric capacitor ensures the permeability of their magnetic fields through the dielectric. The potential on the capacitor plates is one - negative and two magnetic polarities: the north and south magnetic poles.
On fig. Figure 2 shows a diagram explaining the orientation of electrons moving towards the plates of the capacitor C. The electrons arrive at the bottom plate of the capacitor with the north magnetic poles (N) oriented towards its inner surface (Figure 2). Electrons oriented by the south magnetic poles (S) come to the inner surface of the upper plate of the capacitor.

Rice. 2. Scheme of the movement of electrons to the plates of a dielectric capacitor
So electrons - the only carriers of electricity in the wires form on the capacitor plates not opposite electric polarity, but opposite magnetic polarity. There are no protons on the plates of a dielectric capacitor - carriers of positive charges.
2 Discharging a dielectric capacitor
The process of discharging a dielectric capacitor to resistance is the following experimental proof of the correspondence between the reality of the identified electron model and the fallacy of the prevailing ideas that opposite forms are formed on the plates of a dielectric capacitor. electric charges(Fig. 3) .
The scheme of deviation of the compass needles (K) 1, 2, 3 and 4 when the capacitor is discharged to the resistance R at the moment the switch 5 is turned on is shown in fig. 3.
As can be seen (Fig. 1 and 3), at the moment the capacitor discharge process is turned on, the magnetic polarity on the capacitor plates changes to the opposite and the electrons, having turned around, begin to move towards the resistance R (Fig. 2, 3).

Rice. 3. Scheme of deflection of the compass needles (K) at the moment of discharging the capacitor

Rice. 4. Scheme of the movement of electrons from the plates of the capacitor to the resistance R when discharging a dielectric capacitor
Electrons coming from the upper plate of the capacitor are oriented by the south magnetic poles in the direction of movement, and from the bottom - by the north (Fig. 4). Compasses 3 and 4, installed on a set of wires BA, oriented from south to north, clearly fix this fact by deviating the arrows to the right, proving that the vectors of spins and magnetic moments of all electrons in these wires are directed from south to north (Fig. 3, 4 ).
3 Charging electrolytic capacitor
When analyzing the charging process of an electrolytic capacitor, it should be taken into account that there are ions in the electrolytic capacitor that have positive and negative charges, which control the process of potential formation on the plates of the electrolytic capacitor. Now we will see that the presence of an electrolyte in the capacitor does not lead to the appearance of positive charge carriers, that is, protons, in the wires.
An electron is a hollow torus that has two rotations: about the axis of symmetry and about the annular axis of the torus. Rotation about the annular axis of the torus forms the magnetic field of the electron, and the directions of the magnetic lines of force of this field form two magnetic poles: north N and south S.
The rotation of an electron about the central axis is controlled by the kinetic moment
- vector quantity. The magnetic moment of an electron is also a vector quantity, coinciding with the direction of the angular momentum vector. Both of these vectors form the north magnetic pole of the electron (N), and at the other end of the central axis of its rotation, the south magnetic pole (S) is formed. The formation of such a complex structure of an electron is controlled by more than 20 constants.On fig. 5, and the orientation of the ion is shown as an example
in an electric field. A positively charged proton with its north magnetic pole is directed towards a negative (-) charged plate. Since the vectors of the magnetic moments of the electron and proton in the hydrogen atom are directed oppositely, the axial electrons 2 and 3 of the oxygen atom, connecting in a chain with the protons and neutrons of the nucleus of the oxygen atom, form the same magnetic polarity at the ends of the ion axis (Fig. 5, a). This pattern of magnetic polarity is also preserved along the axis of the cluster consisting of these ions (Fig. 5b). The logic of all processes is preserved only if the actions of the charges and magnetic fields of the electron and proton are equivalent.Let's pay attention to main feature structures of the hydrogen atom: vectors of magnetic moments of the electron
and proton are directed along the axis of the atom in opposite directions. This is due to the fact that the approach of the proton and electron is limited by their magnetic poles of the same name. The distribution of magnetic fields in the structure of the ion is shown in Fig. . 5, a. As can be seen, at the ends of the axis of this ion are the northern magnetic poles of the electron and proton. Ion clusters also have a similar polarity (Fig. 5b). It is quite natural that the number of ion clusters forming electrical circuit in a dielectric capacitor is very large.If the role of the electrodes shown in Fig. 5, a, the capacitor plates are made, then when it is charging, the electrons coming from the external network will be oriented by the south magnetic poles at the left capacitor plate and the north magnetic poles at the right plate. This is due to the fact that electrons bring together their opposite magnetic poles, and the approach of an electron to a proton is limited by similar magnetic poles.

Rice. 5. a) - scheme of the ion; diagram of a cluster of two ions
On fig. 6, and the orientation of the ion is shown as an example
in a charged capacitor. A positively charged proton with its north magnetic pole is directed towards the lower negative (-) charged plate of the capacitor. Since the vectors of the magnetic moments of the electron and proton in the hydrogen atom are directed oppositely, the axial electrons of the 2nd and 3rd oxygen atoms, connecting in a chain with the protons and neutrons of the oxygen atom nucleus, form the same magnetic polarity at the ends of the ion axis. This pattern of magnetic polarity is also preserved along the axis of the cluster consisting of these ions. The logic of all processes is preserved only if the actions of the charges and magnetic fields of the electron and proton are equivalent.Reversible Special attention the fact that the upper plate of the capacitor (Fig. 6, a) has electrons on both sides and therefore it seems that they repel each other. However, it must be borne in mind that during the formation of electron clusters, they are connected to each other by opposite magnetic poles, and the same electric charges limit their approach, therefore, the contact of the ion with the upper plate of the capacitor is provided by opposite magnetic poles of electrons. At the bottom plate of the capacitor there are opposite electric charges that bring together the proton of the hydrogen atom and the electron of the capacitor plate. But this rapprochement is limited to their magnetic poles of the same name. This explains the apparent contradictions.


Rice. 6. a) scheme of ion orientation in an electrolytic capacitor; b ) capacitor charging circuit
Thus, the plates of an electrolytic capacitor are charged with opposite electrical polarity and opposite magnetic polarity at the same time. In this case, the plus functions belong to the south magnetic pole of the electron, and the minus functions belong to the north. These poles form both electrical and magnetic polarities on the capacitor plates. Let's follow the process of charging a capacitor to see how the magnetic poles of an electron and a proton form the magnetic and electric polarities of its plates.
The scheme of the capacitor charging experiment is shown in fig. 5b. The most important requirement for the scheme is its orientation from south (S) to north (N). Immediately after the diode, compass 1 (K) is shown, placed on a wire going to capacitor C. The arrow of this compass, deviating to the right at the moment the voltage is turned on, shows the direction of movement of electrons (Fig. 5, b) from point S to the bottom plate of capacitor C. Above compass shows a diagram of the direction of the magnetic field around the wire, formed by moving electrons in it.
Thus, the electrons that have passed through the diode arrive at the bottom plate of the capacitor with oriented spin vectors
and magnetic moments to its inner surface (Fig. 5b). As a result, a northern magnetic potential (N) is formed on this surface, which is equivalent to a negative potential (-).It is quite natural that electrons will come to the upper plate of the capacitor from the network with oriented south magnetic poles (S). The proof of this is the experimental fact of the deviation of the needle of the upper compass 2 (K) to the right (Fig. 5, b). This means that the electrons moving through the wire to the top plate of the capacitor are oriented with the south magnetic poles (S) in the direction of movement.
On fig. 4 is a diagram explaining the orientation of the electrons moving towards the plates of the capacitor C when it is being charged. The electrons arrive at the bottom plate of the capacitor with their north magnetic poles (N) oriented towards its inner surface. Electrons come to the inner surface of the upper plate of the capacitor with oriented south magnetic poles (S).
Let us pay attention to the fact that the directions of orientation of electrons when they move towards the plates of a dielectric capacitor (Fig. 4) are similar to the orientation of electrons when they move towards the plates of an electrolytic capacitor (Fig. 6, b).
So electrons - the only carriers of electricity in the wires form on the plates of an electrolytic capacitor and opposite electrical polarity (+ and -) and opposite magnetic polarity (S and N) at the same time.
4 Discharging an electrolytic capacitor
The process of discharging a capacitor to resistance is the next experimental proof of the correctness of the new interpretation of the direction of electron movement (Fig. 3) in the wires and the fallacy of the prevailing ideas that only opposite electric charges are formed on the capacitor plates.
Schemes of deflection of compass needles (K) 1, 2, 3 and 4 when the capacitor is discharged to resistance R at the moment switch 5 is turned on are shown in fig. 3.
As can be seen (Fig. 2), at the moment the capacitor discharge process is turned on, the magnetic and electric polarities on the capacitor plates change to opposite ones and the electrons, having turned around, begin to move towards the resistance R (Fig. 2).
Electrons coming from the upper plate of the capacitor are oriented by the south magnetic poles in the direction of movement, and from the bottom - by the north. Compasses 3 and 4, installed on a set of wires BA (Fig. 3), oriented from south to north, will clearly fix the fact by deviating the arrows to the right, proving that the vectors of spins and magnetic moments of all electrons in these wires are directed from south to north.
As can be seen, the scheme of electron movement during the discharge of a dielectric capacitor is similar to the scheme of electron movement during the discharge of an electrolytic capacitor (Fig. 3).
And now imagine the moments of opening or closing of the electrical circuit, at which, as you know, the voltage rises sharply. The reason for this phenomenon is that at the moment of opening the electrical circuit there is a phase when part of this circuit is formed by air ions. The total number of electrons in these ions is much greater than the number of free electrons in the wire. As a result, they increase electric potential for that period of time when air ions form an electrical circuit. This is clearly seen in Fig. 5a, where the ion is shown
between the plates of the capacitor. The zone of the broken electrical circuit is filled with the same ions.Lab #6
STUDYING THE PROCESS OF CHARGING AND DISCHARGE OF A CAPACITOR
GOAL OF THE WORK
The study of the processes of charge and discharge of capacitors in RC-circuits, familiarization with the operation of devices used in pulsed electronic technology.
THEORETICAL BASES OF WORK
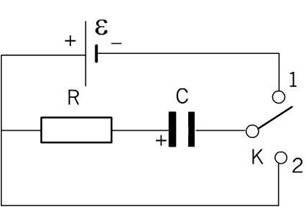 Consider the scheme presented in fig. 1. Circuit includes source direct current, active resistance and a capacitor, the processes of charge and discharge in which we will consider. We will analyze these processes separately.
Consider the scheme presented in fig. 1. Circuit includes source direct current, active resistance and a capacitor, the processes of charge and discharge in which we will consider. We will analyze these processes separately.
Capacitor discharge.
Let the current source e be first connected to the capacitor C through the resistance R. Then the capacitor will be charged as shown in fig. 1. Let's move the key K from position 1 to position 2. As a result, the capacitor, charged to voltage e, will begin to discharge through the resistance R. Considering the current to be positive when it is directed from the positively charged capacitor plate to the negatively charged one, we can write
http://pandia.ru/text/78/025/images/image003_47.gif" width="69 height=25" height="25">, , (1)
Where i- the instantaneous value of the current in the circuit, the minus sign of which indicates that the appearance of current in the circuit i associated with a decrease in charge. q on the condenser
q And WITH- instantaneous values of the charge and voltage on the capacitor.
Obviously, the first two expressions are the definitions of current strength and electric capacity, respectively, and the last one is Ohm's law for a circuit section.
From the last two relations, we express the current strength i in the following way:
http://pandia.ru/text/78/025/images/image006_31.gif" width="113" height="53 src=">. (2)
18. Why is there no direct current source shown in the circuit diagram in this installation?
19. Is it possible to use a generator of sinusoidal voltage, sawtooth voltage in this installation?
20. What frequency and duration of pulses should the generator produce?
21. Why do we need active resistance in this circuit R? What should be its value?
22. What type of capacitors and resistors can be used in this installation?
23. What values \u200b\u200bof capacitance and resistance can have in this circuit?
24. What is the purpose of oscilloscope signal synchronization?
25. How to achieve the optimal type of signal on the oscilloscope screen? What adjustments apply?
26. What is the difference between the charge and discharge circuits of a capacitor?
27. What measurements need to be taken to determine the capacitance of a capacitor in RC-chains?
28. How to evaluate the measurement errors during the operation of the installation?
29. How to improve the accuracy of determining the relaxation time RC-chains?
30. What are the ways to improve the accuracy of determining the capacitance of a capacitor.
The purpose of the work is to study the process of discharging a capacitor to active resistance, determining the relaxation time, and estimating the capacitance of a capacitor.
Instruments and accessories: laboratory setup, power supply, microammeter, capacitor under test, stopwatch.
An electric capacitor or simply a capacitor is a device capable of accumulating and releasing (redistributing) electrical charges. A capacitor consists of two or more conductors (plates) separated by a dielectric layer. As a rule, the distance between the plates, equal to the thickness of the dielectric, is small compared to the linear dimensions of the plates, therefore electric field, which occurs when the plates are connected to a source with voltage U, is almost completely concentrated between the plates. Depending on the shape of the plates, capacitors are flat, cylindrical, spherical.
The main characteristic of a capacitor is its capacitance. C, which is numerically equal to the charge Q one of the plates at a voltage equal to unity:
Let a capacitor with a capacity C included in the electrical circuit (Fig. 1),
Fig.1
containing a constant voltage source U 0, key K and resistor (resistance) R. When the key is closed K the capacitor is charged to voltage U 0. If then the key K open, the capacitor will start to discharge through the resistor R and in the chain there will be electricity I. This current changes with time. Considering the processes occurring in the circuit as quasi-stationary, we apply the laws of direct current for this circuit.
Find the dependence of the discharge current I from time t. To do this, we use the second Kirchhoff rule as applied to the chain R-C(Fig. 2). Then we get:
, (1)
Where I- electric current in the circuit, Q- capacitor charge C. Substituting into equation (1) the value of the discharge current I = - dQ / dt, we get differential equation first order with separable variables:
.
(2)
After integrating equation (2), we find
Q(t) = Q 0 e -t/τ , (3)
Where Q0- initial value capacitor charge, τ = RC is a constant with the dimension of time. It is called relaxation time. Through time τ , the charge on the capacitor decreases by a factor of e.
Differentiating equation (3), we find the law of change of the discharge current I(t):
I(t) = e-t/τ .
I(t) = I 0 e-t/τ, (4)
Where I 0 = - the initial value of the current strength, i.e. current at t = 0.
Figure 3 plots two dependences of the discharge current I from time t corresponding to two different meanings active resistance R 1 and R 2 (τ 1 < τ 2).
Description of the laboratory setup
In this laboratory work, it is proposed to investigate the process of discharging a capacitor in an experimental setup, the scheme of which is shown in Fig. 4.
It consists of a constant voltage source U 0, capacity C, resistors R 1 , R 2 ,R 3 and microammeter. Since the resistors R 1 , R 2 ,R 3 are connected in series, the active resistance of the circuit can be changed using jumpers P, shorting the resistors one by one R 1 , R 2 or both together.
Measurement order. Processing of measurement results
Assemble the electrical circuit according to the diagram in Fig. 4 and, on the instructions of the teacher, select the required value of the resistance of the circuit R.
lock the key K and charge the capacitor C up to voltage U 0. When the capacitor is fully charged, the microammeter will show the maximum current value I 0.
unlock the key K and start the stopwatch at the same time. measure time t0, during which the readings of the microammeter will decrease by 10 times. Determine the time interval ∆t ≈ t0 / 10.
Close the key again K and charge the capacitor.
unlock the key K and record the readings of the microammeter at time intervals Δt, 2Δt, 3Δt, etc. before time 10 Δt. Do these measurements three times, and enter the results in Table 1.
Calculate (average current value) and ratio.
Table 1
| t,s | 0 | Δt | 2Δt | 3Δt | 4Δt | 5Δt | 6Δt | 7Δt | 8Δt | 9Δt | 10Δt |
| I 1 | |||||||||||
| I 2 | |||||||||||
| I 3 | |||||||||||
| /I 0 |
Repeat the experiments three times for different values. R.
Control questions:
What is called a capacitor? Derive the capacitance formula for a flat capacitor.
Derive the formula for the capacitance of a spherical capacitor.




