To study the electrostatic field from the energy point of view, as in the case of considering the intensity, a positively charged point body is introduced into it - a test charge. Let us assume that a uniform electric field, moving from point 1 to point 2 a body introduced into it with a charge q and on the path l, does work A = qEl(Fig. 62, a). If the applied charge is 2q, 3q, ..., nq, then the field will do the work accordingly: 2A, 3A, ..., nA. These works are different in size, so they cannot serve as a characteristic electric field. If we take, respectively, the ratios of the values ​​of these works to the values ​​of the charge of the body, then it turns out that these ratios for two points (1 and 2) are constant values:

If we study the electric field in a similar way between any two of its points, then we will come to the conclusion that for any two points of the field, the ratio of the amount of work to the amount of the charge of the body moved by the field between the points is a constant value, but it is different depending on the distance between the points. The value measured by this Ratio is called the potential difference between two points of the electric field (denoted by φ 2 - φ 1) or voltage U between the points of the field. The scalar quantity, which is the energy characteristic of the electric field and is measured by the work done by it when moving a point body, the charge of which is +1, from one point of the field to another, is called the potential difference between two points of the field, or the voltage between these points. From the definition of potential difference 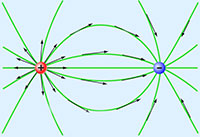voltage U \u003d φ 2 - φ 1 \u003d Δφ.

Every charged body has an electric field around it. With increasing distance from the body to any point of the field, the force with which it acts on the charge introduced into it decreases (Coulomb's law) and at some point in space practically becomes equal to zero. The place where the action of the electric field of a given charged body is not detected is called infinitely distant From him.

If the ball of the electroscope is placed in different points of the electric field of the charged ball of the electrophore machine, then it charges the electroscope. When the electroscope ball is grounded, the electric field of the machine does not affect the electroscope at all. The potential difference between an arbitrary point of the electric field and a point located on the surface of the Earth is called the potential of a given point of the field relative to the Earth. It is measured by work, for the calculation of which you need to know the start and end points of the path. A point on the surface of the Earth is taken as one of these points, and the work of moving the charge is calculated relative to it, and, consequently, the potential of the other point.

If the electric field is formed by a positively charged body (Fig. 62, b), then it itself moves the positively charged body C brought into it to the Earth's surface. The potentials of the points of such a field are considered positive. When the electric field is formed by a negatively charged body (Fig. 62, c), an extraneous force F post is needed to move a positively charged body C to the Earth's surface. The potential of the points of such a field is considered negative.

If the potentials of the points of the field φ 1 and φ 2 are known, then, based on the potential difference formula, we can calculate the work of moving a charged body from one point of the field to another: A \u003d q (φ 2 - φ 1), or A = qU. Therefore, the potential difference is the energy characteristic of the electric field. According to these formulas, the work of moving a charge in a homogeneous and inhomogeneous electric fields is calculated.

Set the unit of voltage (potential difference) in the SI system. To do this, we substitute the value in the voltage formula A \u003d 1 j And q = 1 k:

The unit of voltage - volt - is the potential difference between two points of the electric field, when moving between which a point body with a charge of 1 k, the field does work of 1 j.

electrical voltage.
Potential difference. voltage.

Topic: what is electric voltage and potential difference.

Perhaps one of the most commonly used expressions among electricians is the concept of electrical voltage. It is also called the potential difference and not quite the right phrase, such as voltage, well, the meaning of the names is essentially the same. What does this concept really mean? Perhaps, to begin with, I will give a book formulation: electrical voltage - this is the ratio of the work of the electric field of charges during the transfer of a test charge from point 1 to point 2. well and in simple terms speaking, it is explained thus.

Let me remind you that there are two types of charges, these are positive with a “+” sign and negative with a “-” sign. Most of us in childhood played with magnets, which were honestly obtained from another broken car with an electric motor, where they stood. So, when we tried to bring these same magnets closer to each other, in one case they were attracted, and if one of them was turned the other way around, they repelled accordingly.

This happened because any magnet has two poles, these are south and north. In the case when the poles are the same, then the magnets will repel, but when they are opposite, they will attract. The same thing happens with electric charges, and the force of interaction depends on the number and variety of these charged particles. Simply put, the more “plus” on one object, and on the other, respectively, “minus”, the stronger they will be attracted to each other. Or vice versa, repel the same charge(+ and + or - and -).

Now imagine that we have two small iron balls. If you mentally look into them, you can see a huge variety of small particles that are located from each other on not long distance and incapable of free movement, these are the nuclei of our matter. Around these particles with incredible high speed smaller particles rotate electrons. They can break away from some nuclei and join others, thus traveling all over the iron ball. In the case when the number of electrons corresponds to the number of protons in the nucleus, the balls are electrically neutral.

But if you somehow take away a certain amount, such a ball will tend to attract this same missing amount of electrons to itself, thereby forming around itself positive field with a "+" sign. The more electrons are missing, the stronger it will be. positive field. In the neighboring ball, we will do a turn and add extra electrons. As a result, we get an excess and, accordingly, the same electric field, but with a "-" sign.

As a result, we get two potentials, one of which is eager to receive electrons, and the second one will get rid of them. An excess of tightness arises in the ball, and these particles, around which there is a field, push and push each other out of the ball. And where there is a lack of them, accordingly, something like a vacuum occurs, which tries to draw these electrons. This is a clear example of a potential difference and nothing more than a voltage between them. But, as soon as these iron balls are connected to each other, an exchange will take place and the tension will disappear, since neutrality is formed.

Roughly speaking, this force of the tendency of charged particles to move from more charged parts to less charged parts between two points will be the potential difference. Let's mentally imagine the wires that are connected to the battery from an ordinary flashlight. In the battery itself chemical reaction, which results in an excess of electrons ("-"), inside the battery they are pushed to the negative terminal. These electrons tend to return to their place, from where they were pushed out before.

They don’t succeed inside the battery, so it remains to wait for the moment when they will make a bridge in the form electrical conductor and along which they will quickly run to the positive terminal of the battery, where they are attracted. In the meantime, there is no bridge, then there will be a desire to cross in the form of this very electrical voltage or potential difference(voltage).

I will give some similar example on a different view. There is a regular faucet with water. The tap is closed and, therefore, water will not come out of it, but there is still water inside and moreover, it is there under some pressure, because of this pressure it tends to break out, but the closed tap prevents it. And as soon as you turn the faucet handle, the water will immediately run. So this pressure can be roughly compared with voltage, and water with charged particles. The flow of water itself will this example act as an electric current in the wires themselves, and a closed faucet in the role electrical switch. I gave this example only for clarity, and it is not a complete analogy!

Oddly enough, but people not closely associated with the profession of an electrician, it is quite common to call electrical voltage , expression is voltage and this is an incorrect formulation, since voltage, as we found out, is a potential difference electric charges, and the current is the flow of these charged particles. And it turns out that, pronouncing the voltage, as a result, a slight discrepancy between the concept itself.

Voltage, like all other quantities, has its own unit of measurement. It is measured in Volts. These are the same volts that are written on devices and power supplies. For example, in a regular home socket 220 V, or a battery you bought with a voltage of 1.5 V. In general, I think you understand in general terms, what is this most electrical voltage. In this article, I was based only on a simple understanding of this term and did not go into the depths of formulations and formulas, so as not to complicate understanding. In fact, this topic can be studied much more widely, but it already depends on you and your desire.

P.S. Be careful when working with electricity, high voltage is life threatening.

Potential fields. It can be proved that the work of any electrostatic field when moving a charged body from one point to another does not depend on the shape of the trajectory, just like the work uniform field. On a closed trajectory, the work of the electrostatic field is always zero. Fields with this property are called potential fields. In particular, the electrostatic field of a point charge has a potential character.

The work of a potential field can be expressed in terms of a change in potential energy. The formula is valid for an arbitrary electrostatic field. But only in the case of a homogeneous field, the energy is expressed by the formula (8.19)

Potential. The potential energy of a charge in an electrostatic field is proportional to the charge. This is true both for a homogeneous field (see formula 8.19), and for any other. Therefore, the ratio of potential energy to charge does not depend on the charge placed in the field.

This allows us to introduce a new quantitative characteristic of the field - the potential. The potential of an electrostatic field is the ratio of the potential energy of a charge in the field to this charge.

According to this definition the potential is:

The field strength is a vector and represents the force characteristic of the field; it determines the force acting on the charge at a given point in the field. Potential is a scalar, it is the energy characteristic of the field; it determines the potential energy of the charge at a given point in the field.

If we take a negatively charged plate (Fig. 124) as the zero level of potential energy, and hence the potential, then according to formulas (8.19 and 8.20), the potential of a uniform field is equal to:

Potential difference. Like potential energy, the value of the potential at a given point depends on the choice of the zero level for the reference of the potential. Of practical importance is not the potential itself at the point, but the change in the potential, which does not depend on the choice of the zero level of the potential reference.

Thus, the potential difference (voltage) between two points is equal to the ratio of the work of the field to move the charge from the starting point to the final point to this charge.

Knowing the voltage in the lighting network, we thereby know the work that the electric field can do when moving a unit charge from one socket contact to another along any electrical circuit. We will deal with the concept of potential difference throughout the course of physics.

Unit of potential difference. The unit of potential difference is established using formula (8.24). In the International System of Units, work is expressed in joules and charge in coulombs. Therefore, the potential difference between two points is equal to one if, when moving a charge of 1 C from one point to another, the electric field does work of 1 J. This unit is called a volt

1. What fields are called potential? 2. How is the change in potential energy related to work? 3. What is equal to potential energy charged particle in a uniform electric field? 4. Define potential. What is the potential difference between two points in the field?

The potential difference between points 1 and 2 is the work done by the field forces when moving a unit positive charge along an arbitrary path from point 1 to point 2. For potential fields, this work does not depend on the shape of the path, but is determined only by the positions of the start and end points

the potential is defined up to an additive constant. The work of the forces of the electrostatic field when moving the charge q along an arbitrary path from the starting point 1 to the end point 2 is determined by the expression

The practical unit of potential is the volt. A volt is the potential difference between such points when, when moving one pendant of electricity from one point to another, the electric field does work of one joule.

1 and 2 are infinitely close points located on the x-axis, so that X2 - x1 = dx.

Work when moving a unit of charge from point 1 to point 2 will be Ex dx. The same work is equal to . Equating both expressions, we get

- scalar gradient

function gradient is a vector directed towards the maximum increase of this function, and its length is equal to the derivative of the function in the same direction. The geometric meaning of the gradient is equipotential surfaces (surfaces of equal potential), a surface on which the potential remains constant.

13 Potential charges

Potential of the field of a point charge q in a homogeneous dielectric.

- electrical displacement of a point charge in a homogeneous dielectric D - vector of electrical induction or electrical displacement

Zero should be taken as the integration constant, so that at , the potential vanishes, then

System field potential point charges in a homogeneous dielectric.

Using the principle of superposition, we get:

Potential of continuously distributed electric charges.

- elements of volume and charged surfaces centered at a point

If the dielectric is inhomogeneous, then integration should be extended to polarization charges as well. The inclusion of such

charge automatically takes into account the influence of the environment, and the value does not need to be entered

14 Electric field in matter

Electric field in matter. A substance introduced into an electric field can significantly change it. This is due to the fact that matter consists of charged particles. In the absence of an external field, the particles are distributed inside the substance in such a way that the electric field created by them, on average, over volumes that include a large number of atoms or molecules, is equal to zero. In the presence of an external field, the redistribution of charged particles occurs, and an intrinsic electric field arises in the substance. The total electric field is formed in accordance with the principle of superposition from the external field and the internal field created by the charged particles of matter. The substance is diverse in its electrical properties. The broadest classes of matter are conductors and dielectrics. A conductor is a body or material in which electric charges begin to move under the action of an arbitrarily small force. Therefore, these charges are called free. In metals, free charges are electrons, in solutions and melts of salts (acids and alkalis) - ions. A dielectric is a body or material in which, under the action of arbitrarily big forces charges are displaced only by a small distance, not exceeding the size of the atom, relative to their equilibrium position. Such charges are called bound. Free and bound charges. FREE CHARGES 1) excess electric. charges communicated to a conducting or non-conducting body and causing a violation of its electrical neutrality. 2) Electrical current carrier charges. 3) put. electric charges of atomic residues in metals. RELATED CHARGES the charges of the particles that make up the atoms and molecules of the dielectric, as well as the charges of the ions in the crystal. dielectrics with an ionic lattice.

Potential difference

It is known that one body can be heated more and the other less. The degree of heating of a body is called its temperature. Similarly, one body can be electrified more than another. The degree of electrification of the body characterizes a quantity called the electric potential or simply the potential of the body.

What does it mean to electrify the body? This means telling him electric charge, i.e., add a certain number of electrons to it if we charge the body negatively, or take them away from it if we charge the body positively. In either case, the body will have a certain degree of electrification, i.e., one or another potential, moreover, a positively charged body has a positive potential, and a negatively charged body has a negative potential.

The difference in the levels of electric charges two bodies are called difference electrical potentials or simply potential difference.

It should be borne in mind that if two identical bodies are charged with the same charges, but one is larger than the other, then there will also be a potential difference between them.

In addition, a potential difference exists between two such bodies, one of which is charged and the other has no charge. So, for example, if any body isolated from the earth has a certain potential, then the potential difference between it and the earth (whose potential is considered to be zero) is numerically equal to the potential of this body.

So, if two bodies are charged in such a way that their potentials are not the same, there inevitably exists a potential difference between them.

Everyone knows electrification phenomenon combs when rubbing it against the hair is nothing more than the creation of a potential difference between the comb and human hair.

Indeed, when the comb rubs against the hair, part of the electrons passes to the comb, charging it negatively, while the hair, having lost some of the electrons, is charged to the same extent as the comb, but positively. The potential difference created in this way can be reduced to zero by touching the comb to the hair. This reverse transition of electrons is easily detected by ear if an electrified comb is brought close to the ear. A characteristic crackle will indicate the current discharge.

Speaking above about the potential difference, we had in mind two charged bodies, however the potential difference can also be obtained between different parts (points) of the same body.

So, for example, consider what happens in if, under the action of some external force, we manage to move the free electrons in the wire to one end of it. Obviously, there will be a shortage of electrons at the other end of the wire, and then a potential difference will arise between the ends of the wire.

As soon as we stop the action of the external force, the electrons immediately, due to the attraction of opposite charges, rush to the end of the wire, which is positively charged, i.e., to the place where they are lacking, and electrical equilibrium will again come in the wire.

Electromotive force and voltage

D To maintain an electric current in a conductor, some external source of energy is needed to maintain the potential difference at the ends of this conductor all the time.

These sources of energy are the so-called electric current sources having a certain electromotive force, which creates and maintains a potential difference at the ends of the conductor for a long time.

The electromotive force (abbreviated EMF) is denoted by the letter E. The unit of measure for EMF is the volt. In our country, the volt is abbreviated by the letter "B", and in the international designation - by the letter "V".

So, to get a continuous flow, you need an electromotive force, that is, you need a source of electric current.

The first such current source was the so-called "voltaic column", which consisted of a series of copper and zinc circles lined with leather soaked in acidified water. Thus, one of the ways to get electromotive force is the chemical interaction of certain substances, as a result of which chemical energy is converted into electrical energy. Current sources in which an electromotive force is created in this way are called chemical current sources.

Currently, chemical current sources - galvanic cells and batteries - are widely used in electrical engineering and power industry.

Another main current source that has become widespread in all areas of electrical engineering and the electric power industry are generators.

Generators are installed on power stations and serve as the only current source for power supply industrial enterprises, electric city lighting, electric railways, tram, metro, trolleybus, etc.

Both in chemical sources of electric current (cells and batteries) and in generators, the action of the electromotive force is exactly the same. It lies in the fact that the EMF creates a potential difference at the terminals of the current source and maintains it for a long time.

These clamps are called current source poles. One pole of the current source always experiences a shortage of electrons and, therefore, has a positive charge, the other pole experiences an excess of electrons and, therefore, has a negative charge.

Accordingly, one pole of the current source is called positive (+), the other negative (-).

Current sources are used to power electric shock various devices - . Current consumers are connected to the poles of the current source by means of conductors, forming a closed electrical circuit. The potential difference that is established between the poles of the current source with a closed electrical circuit is called voltage and is denoted by the letter U.

The unit of voltage, like EMF, is the volt.

If, for example, it is necessary to write down that the voltage of the current source is 12 volts, then they write: U - 12 V.

A device called a voltmeter is used to measure or measure voltage.

To measure the EMF or voltage of a current source, you need to connect a voltmeter directly to its poles. In this case, if open, the voltmeter will show the EMF of the current source. If you close the circuit, then the voltmeter will no longer show the EMF, but the voltage at the terminals of the current source.

The EMF developed by the current source is always greater than the voltage at its terminals.