Naći indukciju magnetskog polja koje stvara pravolinijski

Kada jednosmjerna struja prolazi kroz zatvorenu petlju smještenu u vakuumu, za tačku koja se nalazi na udaljenosti od petlje, magnetna indukcija će imati oblik:

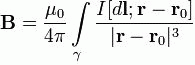
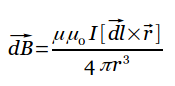
Ako se magnetna igla približi ravnom provodniku kroz koji teče struja, ona će težiti da postane okomita na ravan koja prolazi kroz os provodnika i centar rotacije igle (slika 67).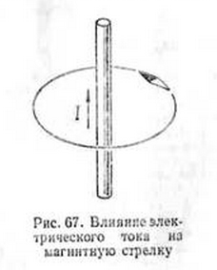

Ovo ukazuje da je igla podložna specijalnim silama koje se nazivaju magnetne sile. Drugim riječima, ako prođe kondukter struja, tada se oko provodnika pojavljuje magnetsko polje.

Magnetno polje se može posmatrati kao posebno stanje prostora koji okružuje provodnike sa strujom.Prilikom izračunavanja magnetnih polja, veličina tzv. tenzija magnetsko polje (označeno H). Magnetna indukcija B i jačina magnetnog polja H povezane su relacijom:

Mjerna jedinica za jačinu magnetnog polja je amper po metru (A/m).

Jačina magnetnog polja u homogenom mediju, kao i magnetna indukcija, zavisi od veličine struje, broja i oblika provodnika kroz koje struja prolazi. Ali za razliku od magnetne indukcije, jačina magnetnog polja ne uzima u obzir utjecaj magnetskih svojstava medija.

34. Proračun po BS zakonu magnetnog polja na osi kružnog namotaja sa strujom Analogija sa električnim poljem dijapola.

Jačina magnetnog polja je omjer mehanička sila, koji djeluje na pozitivni pol ispitnog magneta, na vrijednost njegove magnetske mase ili mehaničke sile koja djeluje na pozitivni pol testnog magneta jedinične mase u datoj tački polja. Intenzitet je predstavljen vektorom H, koji ima smjer vektora mehaničke sile f: .Trenutni element- vektorska veličina jednaka proizvodu struje provodljivosti duž linearnog vodiča i beskonačno malog segmenta ovog vodiča. . Bilješka. Trenutni element ima smjer koji se poklapa sa smjerom ovog segmenta. Biot-Savart-Laplaceov zakon - fizički zakon kako bi se odredio vektor indukcije magnetskog polja generiranog jednosmjernom električnom strujom.

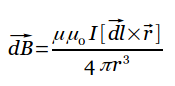
Kružni provodnik koji nosi struju.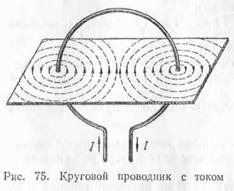

Uzmimo provodnik savijen u krug u obliku zavojnice i propuštamo kroz njega struju (slika 75). Iz crteža se vidi da su magnetne linije zatvorene oko provodnika sa strujom i da imaju oblik krugova. Magnetne linije sa jedne strane ulaze u ravan kružnog provodnika, a sa druge izlaze. Smer kružnog strujnog polja se može odrediti pomoću „pravila gimleta“. Gimlet mora biti postavljen duž ose kružne struje okomito na njegov avion. Ako sada zarotirate ručicu gimleta u smjeru struje u strujnom kolu, tada će translacijsko kretanje gimleta pokazati smjer magnetskog polja. Jačina magnetskog polja u središtu zavojnice sa strujom određena je formulom:

35. Fluks vektora magnetske indukcije (magnetski fluks) i njegovo geometrijsko značenje OG teorema za magnetsko polje.

Tok vektora magnetske indukcije (magnetni tok) kroz područje dS naziva se skalar fizička količina, jednako gdje je Bn=B cos a projekcija vektora B na smjer normale na mjesto dS (a je ugao između vektora n i B), dS=dSn je vektor čiji je modul jednak dS, a njegov smjer poklapa se sa smjerom normale n prema mjestu. Tok vektora B može biti pozitivan ili negativan ovisno o predznaku cos a (određeno izborom pozitivnog smjera normale n). Protok vektora B povezan je sa krugom kroz koji struja teče. U ovom slučaju, pozitivan smjer normale na konturu smo već odredili: on je povezan sa strujom po pravilu desnog vijka. Dakle, magnetni tok koji stvara kolo kroz površinu ograničenu samu sebe uvijek je pozitivan. Tok vektora magnetske indukcije FB kroz proizvoljnu površinu S Za uniformno polje i ravnu površinu koja se nalazi okomito na vektor B, Bn=B=const i Iz ove formule se određuje jedinica magnetnog fluksa Weber (Wb): 1 Wb - magnetni tok koji prolazi kroz ravnu površinu površine 1 m2 koja se nalazi okomito na jednolično magnetsko polje, čija je indukcija jednaka 1 T (1 Wb=1 T×m2). Gaussov teorem za polje B: tok vektora magnetske indukcije kroz bilo koju zatvorenu površinu je nula: Ova teorema odražava činjenicu da ne postoji magnetnih naboja, zbog čega linije magnetske indukcije nemaju ni početak ni kraj i zatvorene su. Dakle, za tokove vektora B i E kroz zatvorenu površinu u vrtložnom i potencijalnom polju rezultati su različiti. Kao primjer, izračunajmo protok vektora B kroz solenoid. Magnetna indukcija jednolikog polja unutar solenoida sa jezgrom magnetske permeabilnosti m, prema tome, jednaka je magnetnom toku kroz jedan zavoj solenoida površine S, a ukupni magnetni tok vezan za sve zavoje solenoida i naziva se fluks veza, . Magnetski moment strujnog kola. Krug sa strujom u magnetskom polju. Iskustvo pokazuje da električne struje međusobno djeluju, na primjer, struje ja privlače, a struje odbijaju. Interakcija struja odvija se kroz polje koje se zove magnetno. Posljedično, pokretni naboji (struje) mijenjaju svojstva prostora koji ih okružuje - stvaraju magnetsko polje u njemu. Ovo polje se očituje u činjenici da sile djeluju na naboje (struje) koji se kreću u njemu. Slično istraživanju električno polje Koristili smo probno punjenje; za proučavanje magnetnog polja koristit ćemo ispitnu struju koja cirkulira u ravnom zatvorenom kolu vrlo malih dimenzija. Takav krug ćemo nazvati probnim krugom. Njegovu orijentaciju u prostoru karakterizira smjer normale n(vektora) na konturu, obnovljenu prema pravilu desnog gimleta: rotiramo ručku desnog gimleta u smjeru struje u kolu, a zatim smjer njegovog translacijskog kretanja će dati smjer normale n(vektora) (vidi sliku 1). Postavljanjem ispitnog kruga u magnetsko polje, otkrivamo da polje teži rotaciji kruga (normalno) u određenom smjeru. 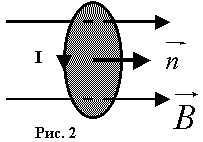Moment koji djeluje na krug ovisi i o svojstvima magnetnog polja u datoj tački i o svojstvima kruga. Ispada da je maksimalna vrijednost momenta proporcionalna IS, tj. Mmax ~ IS, gdje je I struja u kolu, S je površina kola sa strujom (slika 1). Vektorska veličina (1) naziva se magnetni moment kola, koji se u SI mjeri u A×m2. Ispitni krugovi sa različitim pm postavljenim u datoj tački magnetskog polja bit će podvrgnuti različitim maksimalnim momentima M, ali će omjer Mmax/pm biti isti za sva kola; to će biti karakteristika sile magnetskog polja, koja je magnetna indukcija B = Mmax /pm Magnetna indukcija je vektor, čiji se smjer poklapa sa smjerom normale strujnog kola, slobodno uspostavljenog u vanjskom magnetskom polju (vidi sliku 2). Polje vektora B može se predstaviti pomoću linija sile, (vidi sliku 2), kao i vektorskog polja, tako da je B analog E. Magnetna indukcija u SI se mjeri u teslasima: 1 T = 1 Nm/1 A×m2. Tesla je jednaka magnetskoj indukciji jednolikog polja, u kojem na ravno kolo djeluje maksimalni moment od 1 Nm sa strujom koja ima magnetni moment od 1 A m2. Na strujno kolo postavljeno u magnetsko polje sa indukcijom djeluje obrtni moment čija je veličina M =. Rad na pomicanju provodnika i strujnog kola u magnetskom polju. Rad koji izvrši provodnik na struji pri kretanju je brojčano jednak umnošku struje i magnetskog fluksa koji prelazi ovaj provodnik. Razmotrimo strujni krug formiran od fiksnih žica i pokretnog kratkospojnika dužine l koji klizi duž njih (slika 2.17). Ovo kolo se nalazi u vanjskom jednoličnom magnetskom polju B, okomito na ravan kola. Sa smjerom struje I prikazanim na slici, vektor B je kosmjeran sa n. 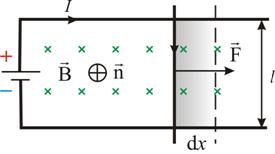Na strujni element I (pokretna žica) dužine l djeluje amperova sila usmjerena udesno: Neka se provodnik l kreće paralelno sa sobom na određenom rastojanju. U ovom slučaju, posao će biti obavljen: Dakle: Formula ostaje važeća ako se provodnik bilo kojeg oblika kreće pod bilo kojim uglom u odnosu na linije vektora magnetske indukcije. Rad pri pomicanju zatvorene petlje sa strujom u magnetskom polju jednak je proizvodu veličine struje i promjene magnetskog fluksa povezanog s ovom petljom. Zamislite pravougaoni krug sa strujom od 1-2-3-4-1 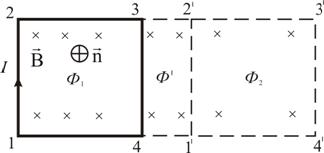(Sl. 2.18). Magnetno polje je usmjereno od nas okomito na ravan konture. Prema tome, magnetski tok koji prodire u kolo usmjeren je duž normale n na krug. Rice. 2.18 Pomerimo ovo kolo paralelno sa sobom na novu poziciju 1"-2"-3"-4"-1". Magnetno polje u opštem slučaju može biti neujednačeno i novi krug će biti probijen magnetnim fluksom . Područje 4-3-2"-1"-4, koje se nalazi između starog i novog kruga, prožima tok. Puni rad pomicanjem kola u magnetskom polju jednak je algebarskom zbiru rada obavljenog pri pomicanju svake od četiri strane kola: , gdje su jednake nuli, jer ove strane ne prelaze magnetni tok kada se kreću (ocrtavaju nultu oblast). Žica 1-2 prekida protok, ali se kreće protiv sila magnetskog polja. Onda opšti posao kretanjem konture: ili ovdje je promjena magnetskog fluksa spojenog na kolo.

B - magnetna indukcija
μ0 - magnetna konstanta
I - jačina struje
r - udaljenost do provodnika

Indukcija magnetnog polja u centru kružne struje (okret)

B - magnetna indukcija
μ - relativna magnetna permeabilnost
μ0 - magnetna konstanta
I - jačina struje
R - radijus

Jačina magnetnog polja naziva se vektorska veličina koja karakterizira magnetsko polje i definirana je na sljedeći način:

Jačina magnetnog polja: beskonačna ravna žica

I - jačina struje
r - udaljenost do provodnika

Jačina magnetnog polja u centru zavojnice

H - jačina magnetnog polja

I - jačina struje
R - radijus

Biot-Savart-Laplaceov zakon.

Biot-Savart-Laplaceov zakon- Magnetno polje bilo koje struje može se izračunati kao vektorski zbir polja stvorenih pojedinačnim odsjecima struja.

Formulacija

Neka jednosmjerna struja teče duž konture γ koja se nalazi u vakuumu - tački u kojoj se traži polje, tada se indukcija magnetskog polja u ovoj tački izražava integralom (u SI sistemu)

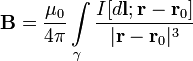
Smjer je okomit na i, odnosno okomit na ravan u kojoj leže, i poklapa se s tangentom na liniju magnetske indukcije. Ovaj smjer se može pronaći pravilom za pronalaženje linija magnetske indukcije (pravilo desnog zavrtnja): smjer rotacije glave vijka daje smjer ako translacijsko kretanje gimleta odgovara smjeru struje u elementu . Veličina vektora određena je izrazom (u SI sistemu)

Vektorski potencijal je dat integralom (u SI)

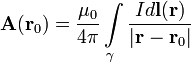
Molekularno-kinetički koncepti strukture materije u različitim agregacijskim stanjima.

Statistička metoda za opisivanje stanja i ponašanja sistema sa više čestica.

Distribucija idealnih molekula gasa po stanju:

Tijela koja nas okružuju (čvrsta, tečna, plinovita) naša osjetila percipiraju kao čvrsta. Međutim, tijela nisu čvrsta, već se sastoje od sitnih čestica nevidljivih golim okom, smještenih ne blizu jedno drugom, već na određenoj udaljenosti. Ove najmanje čestice materije nazivaju se molekuli (umanjeno od latinske riječi za "masu").

Demokrit (5. vek pne) je najmanje čestice koje čine sva tela u svetu nazvao atomima (nedeljivim). Prema Demokritu, atomi imaju različite veličine, težina, oblik itd.

1) Sve supstance se sastoje od sitnih čestica - molekula. Molekul je najmanja čestica supstance koja sve zadržava Hemijska svojstva. Svi molekuli koji se formiraju ovu supstancu, potpuno su isti. Molekule se sastoje od atoma. Atom je najmanja čestica hemijski element(105 komada - 94 prirodnih i 11 umjetnih).

2) Između molekula tijela istovremeno djeluju sile međusobnog privlačenja i odbijanja.

3) Molekuli koji formiraju tijela nalaze se u stanju kontinuiranog nasumičnog kretanja (oscilacije).

Što je temperatura tijela viša, molekuli se brže kreću. Temperatura je mjera prosjeka kinetička energija molekule tijela. Brzina kretanja molekula tijela, koja određuje kinetičku energiju, određuje toplinsko stanje tijela i količinu njegove unutrašnje energije. Haotično kretanje molekula naziva se toplotno.

Razdvajanje molekula na atome naziva se disocijacija. Do disocijacije dolazi pod uticajem 1) visoke temperature, 2) hemijske reakcije, 3) zračenje.

Termodinamika se zasniva na dvije metode proučavanja čestica: termodinamičkoj i statičkoj.

Ponašanje ogromnog broja molekula koji čine makrotela proučava se statističkom metodom, koja se zasniva na činjenici da su svojstva makrotela određena svojstvima molekula, karakteristikama njihovog kretanja (brzina, energija, impuls itd.) i interakcije. Na primjer, temperatura se može izraziti u smislu prosječne kinetičke energije molekularnog kretanja. Statistička metoda daje ideju o mehanizmu toplinskih procesa, posmatrajući ih kao da su iznutra makrotijela; značajno nadopunjuje termodinamičku metodu. Osnovni zakoni termodinamike imaju i statističko značenje.

U gasu koji je u stanju ravnoteže uspostaviće se određena stacionarna (koja se ne menja tokom vremena) distribucija brzina molekula, koja se povinuje dobro definisanom statističkom zakonu. Ovaj zakon je teoretski izveo Maksvel.

Prilikom izvođenja ovog zakona, Maxwell je pretpostavio da se gas sastoji od vrlo veliki broj N identičnih molekula u stanju nasumičnog termičkog kretanja na istoj temperaturi. Takođe se pretpostavljalo da vanjska polja ne djeluju na plin.

Maxwellov zakon je opisan određenom funkcijom f(v), koja se naziva funkcija raspodjele molekularne brzine. Postoje tri oblika pisanja Maksvelove distribucije.

Njutnov drugi zakon za tačkasto telo koje se kreće po kružnici.

Uzimajući u obzir ( ) i () obrtni moment karoserije

Ovaj izraz je analogan drugom Newtonovom zakonu za rotacijsko kretanje, iz kojeg slijedi da je kutno ubrzanje solidan kada se okreće oko fiksne ose, on je direktno proporcionalan momentu i obrnuto proporcionalan momentu inercije u odnosu na ovu os. Iz ovog izraza slijedi da je moment inercije U mjera njegove inercije pri rotacionom kretanju oko fiksne ose. U slučaju translatornog kretanja, mjera inercije, kao što je poznato, je masa tijela.

Navedite primjere i navedite sile koje uzrokuju centripetalno ubrzanje.

Rotacija planeta, gdje gravitacija djeluje kao centripetalna sila. Tamo nema centrifugalne sile. Centrifugalna sila je fiktivna sila koja se uvodi radi lakšeg izračunavanja, kada je lakše izvršiti proračune u neinercijskom sistemu.

Tok magnetnog polja.

Magnetski fluks (fluks vodova magnetne indukcije) kroz konturu je numerički jednak proizvodu veličine vektora magnetske indukcije površinom ograničenom konturom i kosinusom ugla između smjera vektora magnetske indukcije i normale na površinu ograničenu ovom konturom.

Formula za rad Amperove sile kada se kreće pravi provodnik DC u uniformnom magnetnom polju.

Dakle, rad Amperove sile može se izraziti kroz struju u pomaknutom provodniku i promjenu magnetskog fluksa kroz kolo u koje je ovaj provodnik povezan:

Induktivnost petlje.

Induktivnost- fizički količina brojčano jednaka Samoindukovana emf, koji se javlja u kolu kada se struja promijeni za 1 Amper u 1 sekundi.
Induktivnost se također može izračunati pomoću formule:

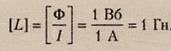gdje je F magnetni tok kroz kolo, I je jačina struje u kolu.

SI jedinice induktivnosti:

Energija magnetnog polja.

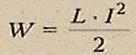Magnetno polje ima energiju. Kao što napunjeni kondenzator ima rezervu električna energija, u zavojnici kroz čije zavoje teče struja, postoji rezerva magnetske energije.

Implementacija svjetlosne interferencije iz konvencionalnih izvora svjetlosti.

Interferencija svjetlosti na tankom filmu. Uslovi za maksimalnu i minimalnu interferenciju svjetlosti na filmu u reflektiranoj i propuštenoj svjetlosti.

Interferentne resice jednake debljine i interferentne resice jednakog nagiba.

1) Fenomen smetnje se uočava u tanki sloj tekućine koje se ne miješaju (kerozin ili ulje na površini vode), u mjehurićima od sapunice, benzinu, na krilima leptira, u zamračenim bojama, itd.

2) 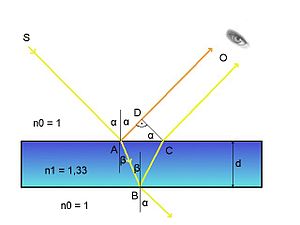interferencija nastaje kada se originalni snop svjetlosti podijeli na dva snopa dok prolazi kroz njega tanki film, na primjer, film nanesen na površinu sočiva obloženih sočiva. Zraka svjetlosti koja prolazi kroz film debljine će se reflektirati dvaput - od njegove unutrašnje i vanjske površine. Reflektirane zrake će imati konstantnu faznu razliku jednaku dvostrukoj debljini filma, uzrokujući da zraci postanu koherentni i interferiraju. Potpuno gašenje zraka će se dogoditi na , gdje je valna dužina. Ako je nm, onda je debljina filma 550:4 = 137,5 nm.

Zraci susjednih dijelova spektra s obje strane nm ne interferiraju u potpunosti i samo su prigušeni, uzrokujući da film dobije boju. U aproksimaciji geometrijske optike, kada ima smisla govoriti o optičkoj razlici putanje zraka, za dvije zrake

Maksimalno stanje;

Minimalno stanje

gdje je k=0,1,2… i dužina optičke putanje prvog i drugog zraka, respektivno.

3)Trake jednakog nagiba

Posebno važno poseban slučaj interferencija svjetlosti koju reflektiraju dvije površine ravno-paralelne ploče kada je tačka posmatranja P u beskonačnosti, tj. Opservacija se vrši ili okom prilagođenim do beskonačnosti, ili na ekranu koji se nalazi u fokalnoj ravni sabirne leće (slika 8.8).

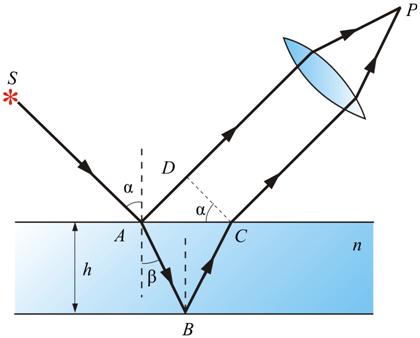
U ovom slučaju, oba zraka koja idu od S do P generiraju se jednim upadnim zrakom i, nakon odbijanja od prednje i stražnje površine ploče, paralelne su jedna s drugom. Optička razlika puta između njih u tački P je ista kao na DC liniji:

Ovdje je n indeks loma materijala ploče. Pretpostavlja se da iznad ploče ima vazduha, tj. . Jer 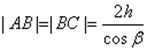, (h je debljina ploče, a uglovi upada i prelamanja na gornjoj strani; ), tada za razliku puta dobijamo

12.7 Proračun indukcije magnetnog polja.

Biot-Savarre-Laplaceov zakon i princip superpozicije omogućavaju izračunavanje indukcije magnetskog polja \(~\vec B\) koju stvara proizvoljni sistem električne struje, u proizvoljnoj tački u prostoru. Da biste to učinili, potrebno je podijeliti sve struje na beskonačno male dijelove \(~(I \Delta \vec l)_k\), zapisati izraze za vektore za indukciju polja \(~(\Delta \vec B)_k\ ) kreirani ovim elementima (koristeći Biot-Savarre-Laplaceov zakon) i zbrojiti rezultirajuće izraze (što omogućava princip superpozicije) za sve dijelove struje

\(~\vec B = \sum_(k) ((\Delta \vec B)_k)\) . (1)

Pogledajmo ponovo dio provodnika sa strujom (slika 29). Izraz za trenutni element \(~I \Delta \vec l\) je također napisan u obliku \(~I \Delta \vec l = \vec j S \Delta l = \vec j \Delta V\) . U slučaju kada električne struje nisu linearne, već prostorno raspoređene (odnosno, teku ne samo duž tanke žice), izraz za trenutni element \(~I \Delta \vec l\) treba zamijeniti ekvivalentnim \(~\vec j \Delta V\) i zbrajanje treba izvršiti po svim elementima zapremine gdje električne struje protok.

Naravno, takvo zbrajanje je često glomazan matematički problem (na kraju krajeva, za to možete koristiti kompjuter), ali sa fizičke tačke gledišta, predstavljena metoda daje kompletno rješenje zadataka.

Razmotrimo nekoliko primjera izračunavanja indukcije magnetskog polja korištenjem gore navedene metode.

12.7.1 Magnetno polje kružne struje.

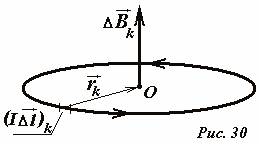
Neka je konstantna električna struja I teče duž ravne kružne konture radijusa R. Nađimo indukciju polja u centru prstena u tački O(Sl. 30). Podijelimo mentalno prsten na male dijelove koji se mogu smatrati pravolinijskim i primijenimo Biot-Savarre-Laplaceov zakon da odredimo indukciju polja koje stvara ovaj element u središtu prstena. U ovom slučaju, vektor trenutnog elementa \(~(I \Delta \vec l)_k\) i vektor \(~\vec r_k\) koji povezuje ovaj element sa tačkom posmatranja (centrom prstena) su okomiti, stoga \(\sin \ alpha = 1\) . Vektor indukcije polja kreiranog odabranim presekom prstena usmeren je duž ose prstena, a njegov modul je jednak

\(~\Delta B_k = \frac(\mu_0)(4 \pi) \frac((I \Delta l)_k)(R^2)\) . (1)

Za bilo koji drugi element prstena situacija je apsolutno slična - vektor indukcije je također usmjeren duž osi prstena, a njegov modul je određen formulom (1). Stoga se zbrajanje ovih vektora izvodi elementarno i svodi na zbrajanje dužina dijelova prstena

\(~B = \sum_k \Delta B_k = \sum_k \frac(\mu_0)(4 \pi) \frac((I \Delta l)_k)(R^2) = \frac(\mu_0)(4 \ pi) \frac(I)(R^2) \sum_k (\Delta l)_k = \frac(\mu_0)(4 \pi) \frac(I)(R^2) 2 \pi R = \frac( \mu_0 I)(2 R)\) . (2)

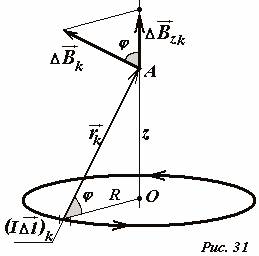
Hajde da zakomplikujemo problem - pronađite indukciju polja u tački A, koji se nalazi na osi prstena na udaljenosti z od njegovog centra (sl. 31). Kao i prije, odabiremo mali dio prstena \(~(I \Delta \vec l)_k\) i konstruiramo vektor indukcije polja \(~(\Delta \vec B)_k\) kreiranog ovim elementom u predmetnoj tački. Ovaj vektor je okomit na vektor \(~\vec r\) koji povezuje odabrano područje sa točkom posmatranja. Vektori \(~(I \Delta \vec l)_k\) i \(~\vec r_k\) su, kao i prije, okomiti, dakle \(\sin \alpha = 1\) . Dakle, prsten ima aksijalna simetrija, zatim ukupni vektor indukcije polja u tački A moraju biti usmjereni duž ose prstena. Do istog zaključka o smjeru vektora ukupne indukcije možemo doći ako primijetimo da svaki odabrani dio prstena ima simetričan na suprotnoj strani, a zbir dva simetrična vektora usmjeren je duž ose prstena. Dakle, da bi se odredio modul ukupnog vektora indukcije, potrebno je sabrati projekcije vektora na osu prstena. Ova operacija nije posebno teška ako uzmete u obzir udaljenosti od svih tačaka prstena do posmatračke tačke su isti \(~r = r_k = \sqrt(R^2 + z^2)\) , a uglovi su također isti φ između vektora \(~(\Delta \vec B)_k\) i ose prstena. Zapišimo izraz za modul željenog ukupnog vektora indukcije

\(~B = \sum_k \Delta B_(zk) = \sum_k \frac(\mu_0)(4 \pi) \frac((I \Delta l)_k)(r^2) \cos \varphi = \frac (\mu_0)(4 \pi) \frac(I \cos \varphi)(r^2) \sum_k (\Delta l)_k = \frac(\mu_0)(4 \pi) \frac(I \cos \ varphi)(r^2) 2 \pi R = \frac(\mu_0 I R)(2 r^2) \cos \varphi\) .

Iz slike slijedi da je \(~\cos \varphi = \frac(R)(r)\), uzimajući u obzir izraz za udaljenost r, dobijamo konačni izraz za vektor indukcije polja

\(~B = \frac(\mu_0 I R)(2 r^2) \cos \varphi = \frac(\mu_0 I R^2)(2 r^3) = \frac(\mu_0 I)(2) \ cdot \frac(R^2)((R^2 + z^2)^\frac(3)(2))\) . (3)

Kao što se i očekivalo, u centru ringa (at z= 0), formula (3) se pretvara u prethodno dobijenu formulu (2).

Zadaci za samostalan rad.

1. Nacrtajte zavisnost indukcije polja (3) o udaljenosti do centra prstena.
2. Uporedi dobijenu zavisnost (3) sa izrazom za modul jakosti električnog polja koje stvara jednoliko naelektrisani prsten (§9.6). Objasnite fundamentalne razlike između ovih zavisnosti.

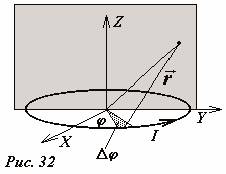
Koristeći opštu metodu o kojoj se ovde raspravlja, moguće je izračunati indukciju polja u proizvoljnoj tački. Sistem koji se razmatra ima aksijalnu simetriju, pa je dovoljno pronaći raspodelu polja u ravni koja je okomita na ravan prstena i koja prolazi kroz njegov centar. Neka prsten leži u ravni xOy(Sl. 32), a polje se izračunava u ravni yOz. Prsten treba podijeliti na male dijelove vidljive iz središta pod uglom Δ φ i sumirati polja kreirana ovim sekcijama. Možete pokazati ( probajte sami), da su komponente vektora magnetske indukcije polja koje stvara jedan odabrani strujni element u tački sa koordinatama ( y,z) se izračunavaju pomoću formula:

\(~\begin(matrica) r_k = \sqrt(x^2 + y^2 - 2xR \cos \varphi_k +1) ; \\ \Delta B_(yk) = -\frac(\mu_0)(4 \pi ) \frac(z \cos \varphi_k)(r^3_k) \Delta \varphi ; \\ \Delta B_(zk) = -\frac(\mu_0)(4 \pi) \frac(1 - y \cos \ varphi_k)(r^3_k) \Delta \varphi . \end(matrica)\) (4)

Neophodno zbrajanje se ne može izvršiti analitički, jer se pri prelasku iz jednog dijela prstena u drugi mijenjaju udaljenosti do točke zbrajanja. Stoga je „najjednostavniji“ način za izvođenje takvog zbrajanja korištenje kompjutera.

Ako je vrijednost vektora indukcije poznata (ili barem postoji algoritam za njeno izračunavanje) u svakoj tački, tada je moguće konstruirati sliku linija magnetskog polja. Očigledno je da algoritam za konstruisanje linija sila vektorskog polja ne zavisi od njegovog fizičkog sadržaja, a o takvom algoritmu smo ukratko govorili prilikom proučavanja elektrostatike.

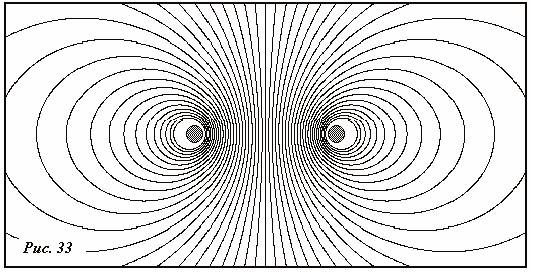
Na sl. 33, uzorak linija polja izračunat je dijeljenjem prstena na 20 dijelova, što se pokazalo sasvim dovoljnim, jer se čak i sa 10 intervala podjele dobio gotovo isti obrazac.

Razmotrimo izraz za indukciju polja na osi prstena na udaljenostima znatno većim od polumjera prstena z >> R. U ovom slučaju, formula (3) je pojednostavljena i poprima oblik

\(~B = \frac(\mu_0 I)(2) \cdot \frac(R^2)((R^2 + z^2)^\frac(3)(2)) \približno \frac(\ mu_0 I)(2) \cdot \frac(R^2)(z^3) = \frac(\mu_0 I)(2 \pi) \cdot \frac(\pi R^2)(z^3) = \frac(\mu_0 p_m)(2 \pi z^3)\) , (5)

gdje je \(I \pi R^2 = IS = p_m\) proizvod jačine struje i površine kruga, odnosno magnetskog momenta prstena. Ova formula je ista (ako, kao i obično, zamijenite μ 0 u brojiocu uključen ε 0 u nazivniku) sa izrazom za jačinu električnog polja dipola na njegovoj osi.

Ova koincidencija nije slučajna; štaviše, može se pokazati da takva korespondencija vrijedi za bilo koju tačku u polju koja se nalazi na velikim udaljenostima od prstena. U stvari, mali krug sa strujom je magnetski dipol (dva identična mala suprotno usmjerena strujna elementa) - stoga se njegovo polje podudara s poljem električnog dipola. Da bismo jasnije istakli ovu činjenicu, na sl. Slika 34 prikazuje sliku linija magnetnog polja prstena, na velikim udaljenostima od njega ( uporedi sa sličnom slikom za polje električnog dipola).

12.7.2 Magnetno polje istosmjerne struje.

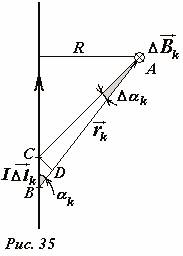
Izračunajmo indukciju magnetskog polja stvorenog beskonačnim vodičem kroz koji struja teče sa silom I(Sl. 35) Metoda proračuna ostaje ista: mentalno dijelimo provodnik na male dijelove \(~I \Delta \vec l_k\). Prema Biot-Savarre-Laplaceovom zakonu u proizvoljnoj tački A, koji se nalazi na udaljenosti R iz provodnika proizvoljni strujni element stvara magnetno polje čiji je vektor indukcije \(~(\Delta \vec B)_k\) usmjeren okomito na ravan koja sadrži provodnik i tačku o kojoj je riječ (na slici 35. - okomito na ravan figure), modul ovog vektora je jednak

\(~\Delta B_k = \frac(\mu_0)(4 \pi) \frac(I \Delta l_k)(r^2_k) \sin \alpha_k\) , (1)

Gdje r k je udaljenost od odabranog dijela provodnika do tačke posmatranja, α k je ugao između provodnika i pravca od trenutnog elementa do tačke posmatranja.

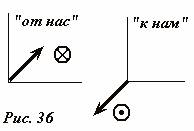
Hajde da se dogovorimo oko još jednog opšteprihvaćenog sporazuma. Često morate crtati vektore okomito na ravninu crtanja. U ovom slučaju, ovi vektori su prikazani u obliku (slika 36): mali krug sa tačkom u centru, ako je vektor usmeren „na nas“ (vidljiva je „ivica“ vektora); krug s križem ako je vektor usmjeren od nas (vidljivo je „pero“ vektora).

Vektori polja koje stvaraju svi ostali dijelovi provodnika su također usmjereni, pa se sumiranje vektora u ovom slučaju svodi na zbir njihovih modula. Ali čak ni izračunati zbroj modula nije lako, jer za različite dijelove vodiča udaljenosti r k and α k su različiti. Ipak, takvo zbrajanje je izvodljivo, njegov rezultat se izražava formulom koja određuje veličinu indukcije magnetskog polja beskonačne struje naprijed

\(~B_k = \sum_k \Delta B_k = \sum_k \frac(\mu_0)(4 \pi) \frac(I \Delta l_k)(r^2_k) \sin \alpha_k = \frac(\mu_0 I)( 4 \pi) \sum_k (\frac(\Delta l_k)(r^2_k) \sin \alpha_k) = \frac(\mu_0 I)(2 \pi R)\) , (2)

izračunavanje posljednje sume ovdje nije dato (koja je jednaka \(~\sum_k \frac(\Delta l_k)(r^2_k) \sin \alpha_k = \frac(2)(R)\)), za sada, vjerujte u valjanost rezultirajućeg izraza, makar samo zato što ima bogato fizičko značenje. Prvo, ova formula se poklapa sa izrazom za jačinu električnog polja koju stvara beskonačna prava linija jednoliko nabijene niti; drugo, odgovara rezultatima A.M. eksperimenata. Ampera o proučavanju interakcije paralelnih struja. Doista, ako jedan provodnik stvara magnetsko polje čija je indukcija obrnuto proporcionalna udaljenosti do vodiča, tada na drugi provodnik djeluje amperova sila proporcionalna indukciji polja, odnosno obrnuto proporcionalna udaljenosti između vodiča. provodnici.

Hajde da sada damo rigoroznu derivaciju formule za iznos koji se pojavljuje u izrazu (2). Najjednostavnije se izvodi operacijom integracije, ali ovdje ćemo dati njegovu geometrijsku derivaciju. Za početak, koristeći sl. 35 transformiramo svaki član ove formule \(~\frac(\Delta l_k)(r^2_k) \sin \alpha_k\) . Imajte na umu da je proizvod \(~\Delta l_k \sin \alpha_k\) jednak dužini segmenta CD, okomito na vektor \(~\vec r_k\) - \(~\Delta l_k \sin \alpha_k = |CD|\) . Omjer dužine ovog segmenta i udaljenosti r k za male dužine strujnih elemenata jednak je malom uglu Δ α k, ispod kojeg je vidljiv odabrani dio provodnika

\(~\frac(\Delta l_k)(r_k) \sin \alpha_k = \frac(|CD|)(r_k) = \Delta \alpha_k\) (3)

(tačnije, ovaj odnos je jednak tangentu ugla, koji je za male uglove jednak samom uglu, mereno u radijanima). Iz iste slike proizilazi da je omjer \(~\frac(r_k)(\sin \alpha_k) = R\) jednak udaljenosti od tačke posmatranja do provodnika i ne ovisi o izboru presjeka provodnika . Uzimajući u obzir ovu relaciju i formulu (2), dobijamo

\(~\frac(\Delta l_k)(r^2_k) \sin \alpha_k = \frac(\Delta \alpha_k)(r_k) = \frac(\Delta \alpha_k \sin \alpha_k)(R)\) .

Dakle, izračunavanje sume (2) svodi se na izračunavanje zbroja \(~\sum_k \Delta \alpha_k \sin \alpha_k\) , u kojem su svi uglovi mali (dakle je i broj članova veliki), neka su uglovi α k varira od nule do neke granične vrijednosti α max.

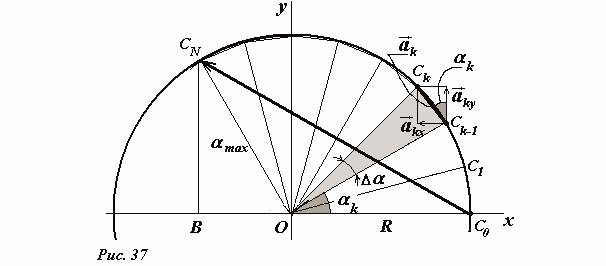
Za izračunavanje ovog iznosa koristit ćemo se umjetnom tehnikom (s njom ćemo se susresti u budućnosti). Uzmimo krug (slika 37) poluprečnika R i razbijte ga tačkama C 0 , C 1 , C 2 , …, C N za male površine, ugaona veličina svaki je jednak Δ α .

Tetive koje formiraju particione tačke će se smatrati vektorima \(~\vec a_0 = \overrightarrow (C_0 C_1), \vec a_1 = \overrightarrow (C_1 C_2), \ldots, \vec a_k = \overrightarrow (C_k) C_(k+ 1)), \ldots\) . Zbir ovih vektora je očigledan - ovo je vektor \(~\vec A\) koji povezuje početnu i završnu tačku kružne podjele:

\(~\sum_k \vec a_k = \overrightarrow (C_0 C_N) = \vec A\) . (4)

Pažnja, ako je vektorska jednakost tačna, onda sličan izraz vrijedi za bilo koju projekciju ovih vektora. Hajde da se predstavimo Kartezijanski sistem koordinate sa ishodištem u centru kružnice, osi Ox koja prolazi kroz početnu tačku. Dužine konstruisanih upisanih vektora jednake su \(~|\vec a_k| = R \Delta \alpha_k\) (tačnije, ovo je dužina luka, ali za male uglove, dužina kontrahovane tetive teži na dužinu luka). Iz slike 37 proizilazi da su projekcije ovog vektora na koordinatne ose jednake, odnosno

\(~a_(kx) = -R \Delta \alpha_k \sin \alpha_k ; a_(ky) = R \Delta \alpha_k \cos \alpha_k\) .

Projiciranjem jednakosti (4) na koordinatne ose dobijamo

\(~\begin(matrix) (\vec A)_x = (\overrightarrow (C_0 C_N))_x = -|C_0 B| = \sum_k a_(kx) = -\sum_k R \Delta \alpha_k \sin \alpha_k \\ (\vec A)_y = (\overrightarrow (C_0 C_N))_y = -|C_N B| = \sum_k a_(ky) = \sum_k R \Delta \alpha_k \cos \alpha_k \end(matrix) \) . (5)

Projekcije ukupnog vektora \(~\vec A\) na koordinatne ose se jednostavno nalaze

\(~\begin(matrix) (\vec A)_x = (\overrightarrow (C_0 C_N))_x = -|C_0 B| = -(R + R \cos (\pi - \alpha_(max))) = R(1 - \cos \alpha_(max)) \\ (\vec A)_y = (\overrightarrow (C_0 C_N))_y = -|C_N B| = R \sin (\pi - \alpha_(max)) = R \sin \alpha_(max) \end(matrica) \) . (6)

Upoređujući izraze (5) i (6) dobijamo tražene formule

\(~\sum_k \sin \alpha_k \Delta \alpha_k = 1 - \cos \alpha_(max); \sum_k \cos \alpha_k \Delta \alpha_k = \sin \alpha_(max)\) . (7)

Još jednom naglasimo da se zbrajanje u ovim formulama vrši u granicama promjene ugla od nule do granične vrijednosti α max.

Ostaje uzeti u obzir da je beskonačan pravi provodnik vidljiv iz bilo koje tačke izvan njega pod uglom α max = π , stoga je tražena količina izražena formulom

\(~\sum_k \frac(\Delta l_k)(r^2_k) \sin \alpha_k = \sum_k \frac(\Delta \alpha_k \sin \alpha_k)(R) = \frac(1 - \cos \pi) (R) = \frac(2)(R)\) ,

Q.E.D.

Procijenimo dužinu “beskonačnog” provodnika u ovom slučaju - koliko puta dužina provodnika mora biti veća od udaljenosti do tačke posmatranja da bi greška u izračunavanju indukcije polja pomoću formule (2) primijenjena na provodnik konačne dužine bio bi zanemarljiv.

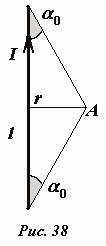
Neka je dužina pravog provodnika l, a indukcija polja se izračunava u tački A, koji se nalazi na udaljenosti r(vjerujemo u to r << l) od centra provodnika (Sl. 38). Koristeći dobijene formule, može se dobiti tačan izraz za indukciju polja u tački koja se razmatra \(~\bar(B) = \frac(\mu_0 I)(2 \pi r) \cos \alpha_0\) , gdje je α 0 - ugao između provodnika i pravca do tačke posmatranja od kraja provodnika.

Ako smatramo da je provodnik beskonačno dug, onda induktivnost polja treba izračunati pomoću formule (koju u ovom slučaju treba smatrati približnom) \(~\tilde(B) = \frac(\mu_0 I)(2 \pi r)\) . Relativna greška ove formule je jednaka

\(~\varepsilon = \frac(\tilde(B) - \bar(B))(\bar(B)) = \frac(1)(\cos \alpha_0) - 1 = \frac(\sqrt(\ lijevo (\frac(l)(2) \desno)^2 + r^2))(\frac(l)(2)) - 1 = \sqrt(1 + 4 \frac(r^2)(l^ 2)) - 1 \približno 2 \frac(r^2)(l^2)\) .

Takva greška će biti napravljena ako je odnos dužine provodnika i udaljenosti do tačke posmatranja jednak \(~\frac(l)(r) = \frac(2)(\varepsilon)\). Dakle za relativnu grešku ε = 1% traženi omjer je \(~\frac(l)(r) \približno 15\). Dakle, u razmatranom slučaju, "beskonačnost" je jednaka 15.