2.4.2. Ohm ve Kirchhoff yasalarının karmaşık biçimi

Ohm yasasının karmaşık formu:

Ỉ=Ủ/ Z veya Ỉ= Y∙Ủ, (2.26)

Ỉ içeri akan akım nerede elektrik devresi,

Ủ – voltaj. Bir elektrik devresine uygulanan

e– elektrik devresinin karmaşık iletkenliği,

Z– elektrik devresinin karmaşık direnci.

Kirchhoff'un birinci yasası. Bir elektrik devresindeki bir düğümde birleşen tellerdeki akımların toplamı sıfırdır:

Kirchhoff'un ikinci yasası. Karmaşık e.m.f.'nin toplamı veya kapalı bir devrede etki eden voltajlar, bu devrenin elemanları arasındaki voltaj düşüşlerinin toplamına eşittir.

(2.28)

Ohm ve Kirchhoff yasaları hem anlık hem de anlık durumlar için geçerlidir. etkili değerler emf. gerilimler ve akımlar.

Etkili (etkili veya rms voltajı) şu ifadeyle belirlenir:

, (2.29)

burada T, 1/f'ye eşit voltaj dalgalanmalarının periyodudur,

f – voltaj salınım frekansı.

Kesinlikle sinüzoidal salınım şekliyle etkin voltaj şuna eşittir: U=Um/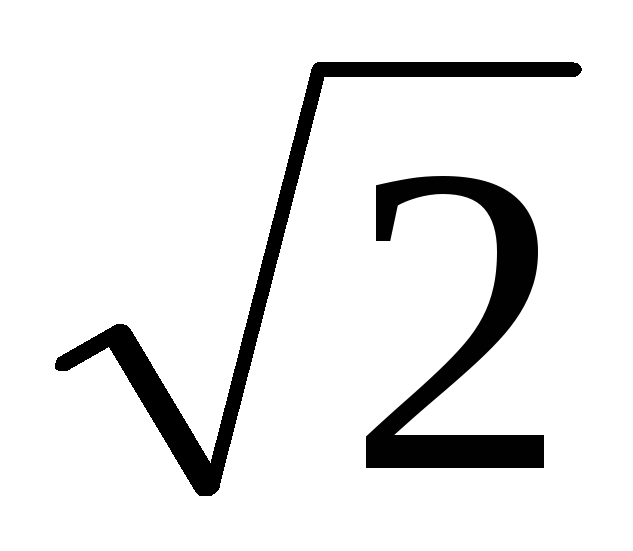

, (2.30)

burada Um maksimum gerilim değeri u(t)'dir.

Etkin emf değerleri de benzer şekilde belirlenir. ve akımlar.

2.4.3. Dönen karmaşık bir düzlemde vektör diyagramlarının oluşturulması

Dönen bir düzlemde vektör diyagramlarının oluşturulmasını kolaylaştırmak için aşağıdaki temel ilkelerin hatırlanması gerekir:

a) Aktif dirençli bir devrede akım ve gerilim aynı fazdadır.

b) Yalnızca kayıpsız endüktif reaktansa sahip ideal bir devrede, faz voltajı akıma 90 derecelik bir açıyla öncülük eder.

c) Kayıpsız tamamen kapasitif reaktansa sahip bir devrede akım, fazdaki gerilimin +90 derecelik bir açıyla önündedir.

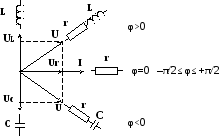
Şekil 2.1 Olası dönüşleri açıklayan anımsatıcı diyagram

r-L-C elemanlarının farklı katılımları için yarıçap vektörleri.

Vektör diyagramlarını oluştururken, analiz edilen devrenin tamamı için ortak olan voltaj veya akım vektörüyle inşaata başlamalısınız. Özellikle devre elemanlarını seri olarak bağlarken, devrenin tüm elemanlarından akan akım vektörünü oluşturarak başlamak gerekir. Devre elemanlarını paralel bağlarken, bir vektör diyagramının oluşturulması, uygulanan toplam voltajın vektörüyle başlamalı ve ardından elektrik devresinin her bir dalından akan akım vektörlerini oluşturmalıdır. R-L-C elemanlarının çeşitli kombinasyonlarından oluşan elektrik devrelerindeki gerilim vektörlerinin olası faz kaymaları, anımsatıcı diyagramda gösterilmektedir (bkz. Şekil 2.1.).

Diyagramdaki ve aşağıdaki yarıçap vektörleri kalın harflerle veya üstlerinde noktalarla (çizgilerle) vurgulanmıştır.

2.4.4. Seri bağlı bir indüktör ve kapasitörden oluşan bir devrede voltaj rezonansı

Direnç, kapasitans ve endüktans değerlerinin zamanla değişmediği ve uygulanan voltaj ve akımlara bağlı olmadığı varsayımı altında bu tür analiz örneklerini ele alalım (bkz. Şekil 2.2).

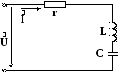
Şekil 2.2 Seri bağlı r-L-C elemanlarının elektrik şeması.

İncelenen devrede meydana gelen süreçler (Kirchhoff'un ikinci yasasına uygun olarak), doğrusal bir integral diferansiyel denklem ile (elemanların zaman içindeki sabit değerleri ve akan akımın büyüklüğünden bağımsız olmaları ile) tanımlanır:

u(t)=ri(t)+Ldi(t)/dt+1/C ∫i(t)dt, (2.31)

neredesin(t) – alternatif akım voltajı kaynaktan salınım devresine beslenen,

BT) - alternatif akım devrede akan,

L – endüktans,

R - aktif direnç indüktörler,

C kapasitörün kapasitansıdır.

Direnç (r), endüktans (L) ve kapasitans (C), voltaj rezonansının mümkün olduğu bir salınım devresi oluşturur. "Voltaj rezonansı" terimi, X l = Xc olduğunda, L ve C devre elemanları üzerindeki alternatif voltajların, kaynaktan devreye sağlanan voltajla karşılaştırıldığında Q kat arttığı anlamına gelir. Q'nun değeri devrenin kalite faktörünü ifade eder, Q=Xc/r'ye eşittir.

Kabul edilen varsayımlar altında denklem (2.31) aşağıdaki biçimde sunulabilir:

u(t)=i(t)*(r+j). (2.32)

Devrenin karmaşık direncinin ifadesi nereden geliyor?

Z=r+j(X l –Xc).

Gerilim rezonansında, X l = Xc olduğunda, Z=r yani devre direnci aktif hale gelir ve devreden geçen akım i(t)max=u(t)/r değerine eşit bir maksimum değere ulaşır.

Bu durumda, bir vektör diyagramının oluşturulması devre için ortak olan akım vektörü (Ỉ) ile başlamalı, ardından gerilim vektörleri oluşturulmalıdır. Şu tarihte: seri bağlantı endüktans bobinleri ve kapasitanslar, X devresinin toplam reaktansı, Xl ve Xc endüktif ve kapasitif dirençlerinin cebirsel farkına eşittir. Böyle bir devreye uygulanan voltaj, akım vektörü ile aynı fazda olan aktif direnç (Ur) boyunca voltaj düşüşü vektörünün vektör toplamı olarak temsil edilebilir; endüktans boyunca gerilim düşüşünün vektörü (U l), fazdaki akımı 90°'lik bir açıyla yönlendirir ve kapasitans (Uc) boyunca gerilim düşüşünün vektörü, akım vektöründen bir açıyla faz olarak geride kalır. 90° Bu durumda aşağıdaki durumlar mümkündür:

a) Endüktif reaktans kapasitif reaktanstan daha büyüktür (X l > X C). Bu durumda giriş voltajı, fazdaki akımı φ açısı kadar ilerletecektir (bkz. Şekil 2.3.).

b) Kapasitif reaktans endüktif reaktanstan daha büyüktür (X l<Х с). При этом ток опережает напряжение на угол φ. Векторная диаграмма тока и напряжений показана на рис. 2.4.

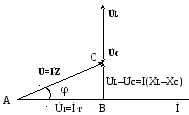
Pirinç. 2.3 Şek. 2.4

V). Endüktif reaktans kapasitif reaktansa eşittir (X l = Xc). Buna göre (X) devresinin toplam reaktansı sıfıra eşit olup devrenin toplam direnci Z=r, yani minimum değerine ulaşır. Bu durumda akım, gerilimle aynı fazda olacaktır; açıφ=0. Bu durum için akım ve gerilimlerin vektör diyagramı Şekil 2'de gösterilmektedir. 2.5.

Gerilim rezonansı olgusu, kendi kendine osilatörlerde yaygın olarak kullanılan kuvars rezonatörlerde de meydana gelir.

e j =j , -j= değerini hesaba katarsak şunu elde ederiz: BEN M = .

Etkili değerlerin komplekslerine geçelim: BEN = sen / X İle ,

Nerede X İle = - karmaşık kapasitans.
Kapasitif elemanın karmaşık akım ve voltaj düzlemindeki vektör diyagramı Şekil 2'de gösterilmektedir. 1.10.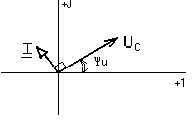

Pirinç. 1.10.

1.6. Sinüzoidal akımlarla doğrusal elektrik devrelerini hesaplamak için karmaşık yöntem
Bildiğiniz gibi herhangi bir elektrik devresi, bir denklem sistemi oluşturup çözerek Kirchhoff yasalarına göre hesaplanabilir. Kirchhoff yasalarının sinüzoidal akım ve gerilimlerin anlık değerlerine uygulanması diferansiyel denklemlere yol açar. Örneğin aktif ve endüktif elemanların seri bağlı olduğu bir devre için Kirchhoff'un ikinci yasasının denklemi şu şekildedir:

.

Bu doğrusal diferansiyel denklemin tam çözümü i(t), bilindiği gibi, u(t) fonksiyonunun formuyla belirlenen özel bir çözümden ve şu şekilde elde edilen homojen diferansiyel denklemin genel çözümünden oluşur: sen(t)=0. Geçerli bileşen sen(t)=0 yalnızca endüktif elemanın manyetik alanındaki enerji rezervleri nedeniyle mevcut olabilir ve aktif eleman üzerindeki enerji kaybı nedeniyle zayıflayacaktır. Böylece, açıldıktan kısa bir süre sonra, devre denkleminin yalnızca kısmi çözümüyle belirlenen bir akım devrede kalır. Bu akıma kararlı durum akımı denir. Gelecekte bu özel modu analiz edeceğiz. İncelenen devreye uygulanan voltajın yasaya göre değiştiğini varsayalım: u(t)=U 0 günah( t+ sen) .

Daha önce gösterildiği gibi (bkz. paragraf 1.5), aktif ve endüktif elemanlarda kararlı durum akımı da sinüzoidal yasaya göre değişecektir: ben(t)=ben M günah( t+  ) .

Sorun, belirli bir frekansta akımın genliğini ve başlangıç ​​fazını bulmakta ortaya çıkar. Bir devrenin bölümlerindeki dal akımlarını veya gerilimlerini belirlemek gerekiyorsa sinüzoidal zaman fonksiyonlarının toplamı gerekir. Bu işlem zahmetli ve zaman alıcı hesaplamalar içermektedir. Hesaplamaların hantallığı, belirli bir frekanstaki sinüzoidal değerin bir değil iki miktar (genlik ve faz) tarafından belirlenmesinden kaynaklanmaktadır. Zamanın sinüzoidal fonksiyonlarını karmaşık sayılarla temsil ederek önemli bir sadeleştirme elde edilmiştir. Sinüzoidal akımlar ve gerilimler için böyle bir temsilin olasılığı daha önce gösterilmiştir (bkz. bölüm 1.4.).

Zamanın gerçek sinüzoidal fonksiyonlarını karmaşık sayılarla temsil etmeye dayanan bir yönteme karmaşık yöntem denir. Zaman fonksiyonunun frekans fonksiyonu tarafından sembolik temsiline dayandığından sembolik yöntem olarak da adlandırılır. Karmaşık yöntem, üstel fonksiyonun çok önemli bir özelliğini kullanır; bu, karmaşık bir üstelin zaman içinde türevini almanın, onu şununla çarpmaya eşdeğer olmasıdır: J ve entegrasyon - şuna göre bölme: J:

; .

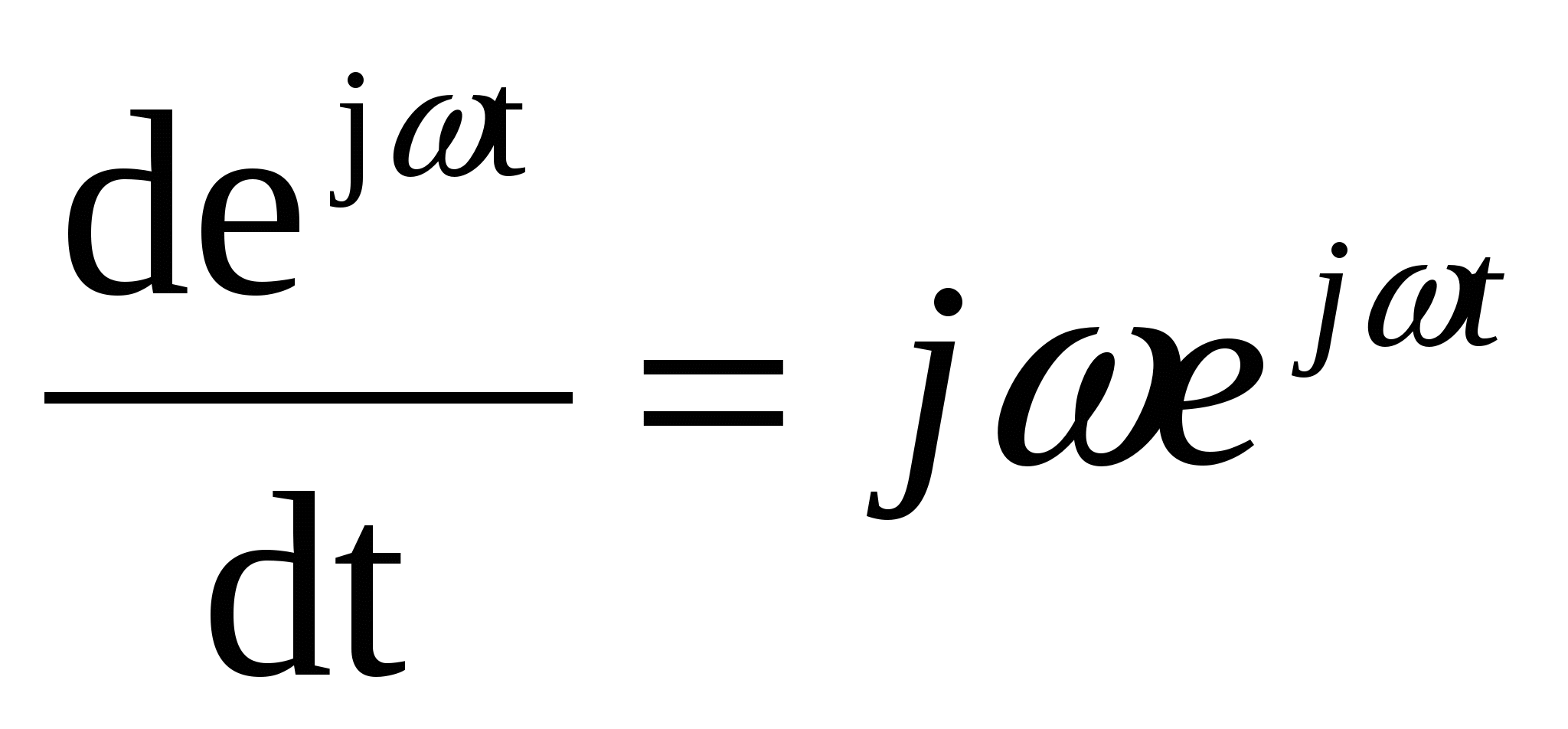Sonuç olarak, Kirchhoff yasalarına göre derlenen tüm diferansiyel denklemlerin yerini cebirsel denklemler alır. karmaşık biçim. Bu cebirsel denklemleri çözerek karmaşık akımları buluyoruz ve onlardan anlık değerlere geçiyoruz. Dolayısıyla karmaşık yöntem, diferansiyel denklemlerin cebirleştirilmesine yönelik bir yöntem olduğundan hesaplamaları önemli ölçüde basitleştirir.
1.7. Ohm ve Kirchhoff yasalarının karmaşık biçimde ifadesi
Sinüzoidal bir akım devresindeki aktif, endüktif ve kapasitif elemanları göz önünde bulundurarak aktif ve reaktif (endüktif veya kapasitif) direnç kavramlarını tanıttık. Genelleştirmek için, karmaşık voltajın karmaşık akıma oranına devrenin karmaşık direnci adını verelim. Z:

.

Direncin modülü ve argümanı sırasıyla etkin değerlerin oranına ve akım ile voltaj arasındaki faz kaymasına eşittir.

Gerçek ve sanal parçalar Z aktif ve reaktif direnç denir. Karmaşık direncin karşılıklılığına karmaşık iletkenlik denir:

.

Modülü ve argümanı tanım gereği Z ve 'nin karşılıklılarıdır. Y'nin gerçek ve sanal kısımlarına aktif ve reaktif iletkenlikler denir. Aktif ve reaktif dirençler ve iletkenlikler arasında bağlantı kuralım.

buradan .

Karmaşık dirençlerin ve iletkenliklerin tanıtılması, Ohm yasasının sabit sinüzoidal mod için karmaşık biçimde tanıtılması anlamına gelir: .

Ohm'un doğru akım yasasından farklı olarak burada akım ve voltajın etkin değerlerinin yanı sıra aralarındaki faz kayması da dikkate alınır.

Şimdi Kirchhoff yasalarını karmaşık biçimde yazalım.

Kirchhoff'un karmaşık formdaki düğümler için birinci yasası şu şekilde yazılmıştır: .

Kirchhoff'un karmaşık formdaki konturlar için ikinci yasası şu şekilde yazılmıştır: .

Karmaşık direnç kavramlarını tanıttıktan ve dalların karmaşık akımları ve gerilimleri için Ohm ve Kirchhoff yasalarını belirledikten sonra, önce devrenin diferansiyel denklem sistemlerini derlemeye ve daha sonra bunları karmaşık akımlar ve gerilimler için cebirsel denklemlere dönüştürmeye gerek yoktur. Bir devreyi karmaşık bir şekilde analiz ederken, devrenin her bir elemanını karmaşık direnci veya iletkenliği ile ve akımları ve gerilimleri karşılık gelen etkili değer kompleksleriyle temsil etmek uygundur. Sonuç, karmaşık bir devre eşdeğer devresidir. Bu şemada, her bir pasif dal, karmaşık dirençli iki terminalli bir ağ olarak temsil edilebilir ve her aktif dal, karmaşık EMF'ye ve iç dirence sahip bir kaynak olarak temsil edilebilir.

Böyle bir eşdeğer devre dirençli bir devre biçiminde olacaktır, ancak gerçek değerler yerine devre karmaşık akım, voltaj, emf ve direnç değerlerine sahip olacaktır.

İLE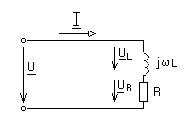
Büyüklüklerin karmaşık doğası, sinüzoidal akımlar ve kararlı durumdaki gerilimler arasındaki faz kaymasının dikkate alınması ihtiyacını yansıtır. Karmaşık eşdeğer devreler için durum denklemleri dirençli DC devrelerine benzer şekilde derlenir. Bu nedenle bir devreyi entegre bir şekilde analiz ederken doğru akım için geçerli olan tüm yöntemleri kullanabilirsiniz:

Devrelerin eşdeğer dönüşüm yöntemleri (elemanların paralel ve seri bağlantısı, yıldız-üçgen dönüşümü ve tersi, gerilim ve akım kaynaklarının dönüşümü);

Orantılı büyüklükler yöntemi;

Düğüm potansiyeli yöntemi;

Döngü akımı yöntemi;

Eşdeğer üreteç yöntemi;

Örtüşme ilkesi, karşılıklılık.

Resmi olarak, karmaşık bir şekilde analiz ile dirençli devrelerin doğru akım kullanılarak analizi arasındaki fark, yalnızca tüm denklemlerin katsayılarının ve değişkenlerin karmaşık büyüklükler olacağı olacaktır.

Karmaşık bir denklemdeki her terim bir vektör olarak ve denklemin kendisi de vektörlerin toplamı olarak temsil edilebildiğinden, karmaşık yöntem, analitik hesaplamalara görsel grafik çizimler - vektör diyagramları - eşlik etmeyi mümkün kılar.

Belirli devreleri hesaplamak için karmaşık bir yöntemin kullanımını düşünelim.
1.8. Sinüzoidal akım devresinde gerçek indüktör
İşte bobinin toplam karmaşık direnci: Z =R+j L

Gerçek bir indüktör, endüktansa ek olarak, yapıldığı telin dönüşlerine karşı aktif bir dirence sahiptir. Bu nedenle, karmaşık bir eşdeğer devre, seri olarak bağlanan endüktif ve aktif dirençlerden oluşacaktır, Şekil 2.1. 1.11.

Kirchhoff'un etkin gerilme değerlerinin kompleksleri için ikinci yasasına göre, toplam gerilme

sen= sen L+ sen R =jL BEN+R BEN=(jL+R) BEN=Z ben

aktif ve reaktif (endüktif) bileşenlerden oluşur.

Pirinç. 1.11.
Modül ve direnç argümanı: z=,

sırasıyla gerilim ve akım arasındaki genlik oranını ve faz kaymasını belirleyin. Mevcut kompleks eşittir ,

nerede  sen-Uygulanan voltajın başlangıç ​​fazı.

Bu nedenle, gerçek bir indüktördeki sinüzoidal akımın anlık değerinin ifadesi şu şekildedir:

.

Akım, devreye uygulanan voltajdan belli bir açıyla faz olarak geride kalır  Bobinin aktif ve endüktif reaktansları arasındaki orana bağlı olarak.

Ortaya çıkan karmaşık ilişkiler bir vektör diyagramında gösterilebilir (Şekil 1). 1.12.

Pirinç. 1.12.
Seri bağlı elemanlar için ortak olan akım vektörü başlangıç ​​vektörü olarak alınır ve isteğe bağlı bir yönde, genellikle yatay olarak çizilir.

Vektör sen R vektör boyunca yönlendirilir BEN fazda olduğu için ve vektör sen L Mevcut vektörü 90 o ilerleterek, onu saat yönünün tersine akıma dik olarak inşa ediyoruz. Bu iki vektörün geometrik toplamı vektörü verir sen indüktöre uygulanan voltaj. Vektör sen faz vektörü ilerletir BEN bir açıyla  . Başlangıç ​​gerilim fazı ise  sen verildiğinde, karmaşık koordinat sisteminin eksenlerini çizmek ve geometrik ölçümlerle belirlemek mümkündür.  Ben ve bizi ilgilendiren diğer parametreler.

Bununla birlikte, gerçek bir indüktörün terminallerindeki toplam voltajın aktif ve endüktif bileşenlerin toplamı olarak temsilinin resmi olduğu ve gerçek bir devrede mevcut olmadıkları ve bir voltmetre ile doğrudan ölçülemedikleri unutulmamalıdır.

1.9. Sinüzoidal bir akım devresinde gerçek bir indüktör ve kapasitörün kayıpsız seri bağlantısı
Endüktif bobinli ve kapasitörlü bir seri alternatif akım devresi, R, L, C elemanlarından oluşan karmaşık bir eşdeğer devre ile temsil edilebilir, Şekil 2.1. 1.13.

Pirinç. 1.13.
Uygulanan gerilimi devre elemanları üzerindeki gerilimlerin toplamı olarak yazıyoruz:

u= sen R +u L +u C

veya karmaşık biçimde: sen = sen R + sen L + sen C .

DERS 7 SERİ İLE DEVRE ANALİZİ

ALICILARIN BAĞLANMASI

Ders taslağı

4. Gerilim rezonansı

1. Alternatif akım devrelerinin temel yasaları

İÇİNDE Alternatif akım devrelerinde Ohm kanunu tüm değerler için karşılanırken, Kirchhoff kanunları sadece faz ilişkilerini dikkate alan anlık ve karmaşık değerler için karşılanır.

Kirchhoff'un birinci yasası. Bir düğümdeki anlık akım değerlerinin cebirsel toplamı:

∑ ben k = 0,

k= 1

veya bir düğümdeki akımların karmaşık değerlerinin cebirsel toplamı sıfıra eşittir:

∑ ben k = 0 .

k= 1

Kirchhoff'un ikinci yasası. Devredeki alıcılardaki anlık voltaj değerlerinin cebirsel toplamı, aynı devrede etki eden EMF'nin anlık değerlerinin cebirsel toplamına eşittir:

Kirchhoff yasalarına göre derlenen denklemlere elektriksel durum denklemleri denir.

1. Alternatif akım devrelerinin temel yasaları

Alıcıların seri bağlantısıyla eşdeğer bir devre Şekil 2'de gösterilmektedir. 7.1.

Süreçleri analiz etmek için Kirchhoff'un ikinci yasasına dayanan denklemi karmaşık biçimde kullanıyoruz:

U = UR + UL + UC.

Ohm kanununa göre ifade edilen gerilim değerlerini bu denklemin yerine koyalım:

U = R I+ j XL I− j XC I= [ R+ j(XL − XC ) ] I= Z I,

burada Z devrenin karmaşık direncidir.

Açıkça görülüyor ki

Z = R+ j(XL − XC ) = R+ j X,

burada R – aktif direnç, X – reaktans.

Alıcıların seri bağlantısı olan bir devre için karmaşık biçimde Ohm yasası:

U = ZI.

Reaktans X pozitif veya negatif olabilir.

X L > X C ise reaktans X > 0. Bu durumda zincir

endüktif bir karaktere sahiptir.

Reaktans X< 0 , еслиX L < X C . Тогда цепь имеет емкостный характер.

2. Bir vektör diyagramının oluşturulması

Genellikle onu inşa ederken karmaşık düzleme bağlı değildirler, çünkü yalnızca karşılıklı düzenleme vektörler.

Bir vektör diyagramının oluşturulması, belirli bir devre için ortak olan büyüklüklerin bir vektörüyle başlar. Elemanları seri olarak bağlarken,

DERS 7. ALICILARIN SERİ BAĞLANTISI İLE DEVRE ANALİZİ

2. Bir vektör diyagramının oluşturulması

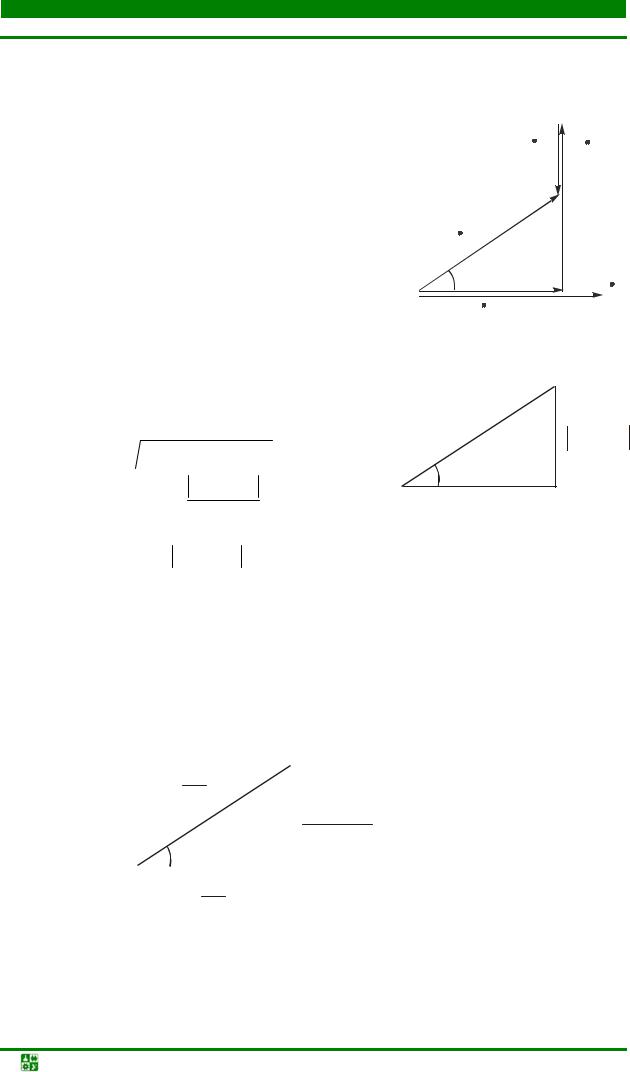
miktar günceldir. Diyagramın türü devrenin yapısına bağlıdır. Doğası gereği aktif-endüktif olan bir devre için bir vektör diyagramının yapısı, yani X L > X C ve X > 0, Şekil 2'de gösterilmektedir. 7.2.

Giriş voltajı, faz kayması dikkate alınarak üç ideal eleman üzerindeki voltajların toplamıdır. Direnç üzerindeki voltaj akımla aynı fazdadır. Endüktif elemandaki voltaj akıma 90° önde, kapasitif elemanda ise 90° geride kalıyor.

Bir vektör diyagramı oluşturulurken elde edilen OAB üçgeni Şekil 2'de gösterilmektedir. 7.3.

Açı φ = ψu − ψi – faz kayma açısı

ka ve tam voltaj.

OAB üçgeni, Kirchhoff yasalarının geçerli olmadığı etkin değerlerle çalışmayı mümkün kılar:

U = UR 2 + (UL - UC ) 2 ,

Ark tg U L − U C ,

U R = Ucos ϕ , UL − UC = Usin ϕ .

UL-UC

O A U R

3. Direnç ve güç üçgenleri

Gerilim üçgeninin tüm taraflarını I akımına bölersek, buna benzer bir direnç üçgeni elde ederiz (Şekil 7.4), burada Z devrenin toplam direncidir, R aktif dirençtir, X reaktanstır.

Alıcıları seri olarak bağlarken Ohm'un etkili değerler yasası şu şekildedir:

DERS 7. ALICILARIN SERİ BAĞLANTISI İLE DEVRE ANALİZİ

3. Direnç ve güç üçgenleri

U = ZI.

Direnç üçgeninin özelliklerinden aşağıdaki ilişkileri elde ederiz:

ϕ açısı devre dirençlerinin oranına bağlıdır.

Toplam ve karmaşık direnç formüllerinin karşılaştırılması, toplam direncin karmaşık direncin modülü olduğu sonucuna varmamızı sağlar. Direnç üçgeninden karmaşık direncin argümanının ϕ açısı olduğu açıktır.

Bu nedenle şunu yazabiliriz:

Z = R + jX = Z e j ϕ .

Herhangi bir sayıda seri bağlı alıcının empedansı

Z = (∑ R) 2 + (∑ XL - ∑ XC ) 2 .

Gerilim üçgeninin tüm taraflarını akımla çarparak bir güç üçgeni elde ederiz (Şekil 7.5).

Aktif güç

P = UR I= R I2 = U Simgeler ϕ

jeneratörden alıcıya tek yönde iletilen enerjiyi karakterize eder. Dirençli unsurlarla ilişkilidir.

U ben= S

UL – UC I= Q

UR ben= P

Reaktif güç Q = U L − U C I = X I 2 = U I sinϕ karakterize eder

Devrede sürekli olarak dolaşan ve üretilmeyen enerjinin bir kısmı faydalı iş. Reaktif elementlerle ilişkilidir.

Toplam (görünen) güç S = U I = P 2 + Q 2.

DERS 7. ALICILARIN SERİ BAĞLANTISI İLE DEVRE ANALİZİ

3. Direnç ve güç üçgenleri

Aktif güç watt (W), reaktif güç reaktif volt amper (var) ve görünen güç volt amper (VA) cinsinden ölçülür.

4. Gerilim rezonansı

Endüktif bir bobin ve bir kapasitör, karşılıklı olarak baskılayıcı antipodlardır. Birbirlerinin eylemlerini tamamen telafi ettiklerinde devre

bir rezonans modu gözlenir.

Endüktif bobinler ve kapasitörler seri bağlandığında voltaj rezonansı meydana gelir. Gerilim rezonans koşulu: giriş reaktansı X sıfırdır.

Eşdeğer devresi Şekil 2'de gösterilen bir devre için rezonans modunu ele alalım. 7.1.

Rezonansta

X =X L −X C =0 .

Dolayısıyla X L = X C.

X L = L ω ve X C = C 1 ω olduğundan, rezonansta L ω0 = C 1 ω 0. O halde LC ω0 2 = 1. Devrede voltaj rezonansının elde edilmesi bunu takip eder.

pirinç. 7.1 endüktansı L, kapasitansı C ve frekansı ω değiştirilerek değiştirilebilir. Döngüsel rezonans frekansı

Devre tamamen aktiftir.

Gerilim rezonans değeri:

1. U L U C'deki elektrikli güç cihazlarında çoğu durumda bu durum istenmeyen bir durumdur,

DERS 7. ALICILARIN SERİ BAĞLANTISI İLE DEVRE ANALİZİ

4. Gerilim rezonansı

beklenmedik aşırı gerilimlerin ortaya çıkmasıyla ilişkilidir.

2. Elektrik iletişim mühendisliğinde (radyo mühendisliği, kablolu telefon), otomasyonda, voltaj rezonansı olgusu, bir devreyi belirli bir frekansa ayarlamak için yaygın olarak kullanılır.

Kendi kendine test soruları

1. Hangi değerler için elektriksel büyüklükler Kirchhoff yasaları yerine getirildi mi?

2. Empedans modülü nedir?

3. Karmaşık direnişin argümanı nedir?

4. Aktif, reaktif ve karmaşık direnç birbiriyle nasıl ilişkilidir?

5. Bir devrenin empedansı nasıl hesaplanır?

6. Gerilim ve akım arasındaki μ açısı neye bağlıdır?

7. Güç tüketimi nedir?

8. Hangi enerji aktif güçle karakterize edilir?

9. Hangi enerji reaktif güçle karakterize edilir?

10. Aktif, reaktif ve görünen güç hangi birimlerde ölçülüyor?

11. Gerilim rezonansının koşulu nedir?

12. Gerilim rezonansının anlamı nedir?