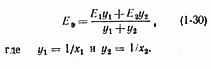Short circuit current formula. Calculation of single-phase short-circuit current
IN this example consider current calculation single-phase circuit to the ground (OZZ) for a 10 kV substation (Substation diagram is shown in Fig. 1). Relay protection and automation of all feeders are made on SEPAM S40 microprocessor terminals (manufactured by Schneider Electric)
Fig.1 - Scheme of a 10 kV substation
1. To improve the accuracy of our calculations when determining the OZZ we use a method based on the determination of the specific capacitive current ground fault. (Also, the values of the specific capacitive earth fault current can be used from the reference data in Table 1, or taken from specifications cables provided by the manufacturer)
- Uph - phase voltage networks, kV;
- ω=2Пf=314(rad/s);
- Co - capacitance of one phase of the network relative to the ground (μF / km);
2. After we have determined the specific capacitive earth fault current, we calculate the intrinsic capacitive current of the cable line:

The calculation results are entered in table 2
Table 2 - Calculation results
| Connection name | Protection relay type | cable brand, section, mm.kv |
Length, km | Specific capacitive ground fault current Ic, A/km | Own capacitive current of the cable line Ic.fid.max, A |
|---|---|---|---|---|---|
| CL-10 kV No. 1 | SEPAM S40 | APvEVng-3x120 | 0,5 | 1,89 | 0,945 |
| CL-10 kV No. 2 | SEPAM S40 | APvEVng-3x95 | 0,3 | 1,71 | 0,513 |
| CL-10 kV No. 3 | SEPAM S40 | APvEVng-3х70 | 0,7 | 1,55 | 1,085 |
| CL-10 kV No. 4 | SEPAM S40 | APvEVng-3x95 | 0,3 | 1,71 | 0,513 |
| KL-10 kV No. 5 | SEPAM S40 | APvEVng-3х70 | 0,2 | 1,55 | 0,31 |
| CL-10 kV No. 6 | SEPAM S40 | APvEVng-3x95 | 0,6 | 1,71 | 1,026 |
3. Calculate the current of protection operation, while detuning from its own capacitive current according to the formula ( this condition provides failure of protection in case of external single-phase earth fault):
- Kn - reliability coefficient (taken equal to 1.2);
- Кbr is the "throw" factor, which takes into account the inrush of the capacitive current at the moment when the fault occurs;
- Ic.feed.max – maximum capacitive current of the protected feeder.
The primary tripping current of the protections is:
- - KL-10 kV No. 1 Iсз= 1.134 A;
- - KL-10 kV No. 2 Iсз= 0.62 A;
- - KL-10 kV No. 3 Iсз= 1.3 A;
- - KL-10 kV No. 4 Iсз= 0.62 A;
- - KL-10 kV No. 5 Iсз= 0.37 A;
- - KL-10 kV No. 6 Iсз= 1.23 A
4. We check the sensitivity of the protections, taking into account that the minimum number of included lines will be included, in our case these are all connections that are on the section.
I draw your attention to the fact that the sensitivity coefficient according to the EIC paragraph 3.2.21 is equal to: for cable lines- 1.25, for overhead lines- 1.5. In the book "Calculation of relay protection and automation of distribution networks. M.A. Shabad -2003" Kch = 1.5-2.0 is given. In this calculation, I accept the sensitivity coefficient according to the PUE. Which sensitivity factor to accept, choose for yourself.

Where:
IcΣmin - the smallest real value of the total capacitive current.
In my case, the smallest real value of the total capacitive current is the total capacitive current by section:
Section I - IcΣmin = 2.543 (A);
II section - IcΣmin = 1.849 (A);
5. We determine the response time of protections against OZZ:
For all outgoing cable lines of 10 kV, the response time of the protections is assumed to be 0.1 sec.
Table 3 - The results of calculations of the operation of protections against SPE
| Connection name | Protection relay type | Primary current actuation Iсз, A |
Protection response time, sec | Sensitivity coefficient, Kh |
|---|---|---|---|---|
| CL-10 kV No. 1 | SEPAM S40 | 1,134 | 0,1 | 1,4 > 1,25 |
| CL-10 kV No. 2 | SEPAM S40 | 0,62 | 0,1 | 3,27 > 1,25 |
| CL-10 kV No. 3 | SEPAM S40 | 1,3 | 0,1 | 1,12 |
| CL-10 kV No. 4 | SEPAM S40 | 0,62 | 0,1 | 2,2 > 1,25 |
| KL-10 kV No. 5 | SEPAM S40 | 0,37 | 0,1 | 4,2 > 1,25 |
| CL-10 kV No. 6 | SEPAM S40 | 1,23 | 0,1 | 0,67 |
For connections CL-10 kV No. 3 and No. 6, the sensitivity of the protection is not enough, so we must use instead of the Sepam S40 terminal → the Sepam S41 or S42 terminal, which will allow you to perform directional zero sequence protection.
In order not to spend a lot of time on manual calculation, the following was done:
Bibliography:
- 1. Calculations of relay protection and automation of distribution networks. M.A. Shabad -2003
- 2.RD 34.20.179 Typical instruction for compensation of capacitive earth fault current in electrical networks 6-35 kV - 1993
- 3. Earth faults in 6–35 kV networks. Calculation of settings of non-directional current protection. Shalin A.I. // News of Electrical Engineering. – 2005
Details Created: 24 August 2011
I to the current of a single-phase short circuit, A; U f phase voltage of the network, V; Z t total resistance of the transformer to the current of a single-phase short circuit to the case, Ohm; Z c impedance phase wire-neutral wire, Ohm.
This formula allows the error of the obtained results within ±10%. For a more accurate calculation short circuit it is necessary to use GOST 28249-93.
The main component of this formula is the impedance of the circuit phase wire - neutral wire Z c. It is found in 2 ways:
Wire parameters and contact resistances are known
If the parameters of the wire and the transient resistances are known, then the value of the impedance of the circuit is calculated by the formula:
Rf active resistance phase wire, Ohm; r n active resistance neutral wire, Ohm; r a is the total active resistance of the phase-zero circuit contacts (terminals at the inputs and outputs of devices, detachable contacts of devices, contact at the short circuit point), Ohm; x f "internal inductive resistance of the phase wire, Ohm; x n" internal inductive resistance of the neutral wire, Ohm; x" external inductive resistance of the phase-zero circuit, Ohm.
The total resistivity of the phase-to-zero loop is known
With a known total resistivity of the phase-zero loop, the formula is used:
Z f-0 full resistivity loops phase - zero, depending on the material and cross-section of the wire, Ohm / km; - wire length, km.
If the circuit contains wires of different cross-sections and lengths, then you need to summarize the obtained values Z c.
An example of finding the current of a single-phase short circuit
For clarity, let's look at an example of finding single-phase short circuit current.
Let there be a circuit to which an electrical receiver is connected. We know the parameters of the supply transformer, the length and cross section of the line wires. It is necessary to find out the short-circuit current at the terminals of the electrical receiver. To do this, we will compose an algorithm of actions.
a) Change in current during a short circuit
The current during a short circuit does not remain constant, but changes, as shown in Fig. 1-23. It can be seen from this figure that the current, which increased at the first moment of time, decays to a certain value, and then, under the action of an automatic excitation controller (ARC), reaches a steady value.
The period of time during which a change in the magnitude of the short-circuit current occurs is called a transient process. After the change in the magnitude of the current stops and until the moment the short circuit is turned off, the steady state short circuit continues. Depending on whether the relay protection settings are selected or the electrical equipment is checked for thermal and dynamic stability, we may be interested in the current values in different moments time k.z.
Since any network has certain inductive resistances that prevent an instantaneous change in current in the event of a short circuit, its value does not change abruptly, but increases along certain law from normal to emergency.
To simplify the calculation and analysis, the current passing during transition process short circuit, is considered as consisting of two components: aperiodic and periodic.
Aperiodic is the current component constant in sign i a, which occurs at the time of a short circuit and decays relatively quickly to zero (Fig. 1-23).
The periodic component of the current short circuit at the initial time I nmo is called the initial short circuit current. The value of the initial current to. are used, as a rule, to select settings and check the sensitivity of relay protection. The initial short-circuit current is also called supertransitional, since to calculate it, the so-called supertransitional resistance of the generator and supertransitional e are introduced into the equivalent circuit. d.s.
Steady current short circuit represents a periodic current after the end of the transient, due to both the attenuation of the aperiodic component and the action of the AEC. Total short-circuit current is the sum of the periodic and aperiodic components at any moment of the transient process. Maximum instantaneous value full current is called shock current to. and is calculated when checking electrical equipment for dynamic stability.
As noted above, to select the settings and check the sensitivity of the relay protection, the initial or supertransient short-circuit current is usually used, the calculation of which is the most simple. Using the initial current in the analysis of high-speed protections and protections with short time delays, the aperiodic component is neglected. The admissibility of this is obvious, since the aperiodic component in high voltage networks decays very quickly, within 0.05-0.2 s, which is usually less than the duration of the protections under consideration.
At k.z. in a network powered by a powerful power system, the generators of which are equipped with ARVs that maintain a constant voltage on its tires, the periodic component of the current in the process of short circuit. does not change (Fig. 1-23,b). Therefore, the calculated value of the initial short-circuit current. in this case, it can be used to analyze the behavior of relay protection, acting with any time delay.
In networks powered by a generator or a system of a certain limited power, the voltage on the buses of which is in the process of short circuit. does not remain constant, but varies significantly, the initial and steady current short circuit. are not equal (Fig. 1-23, a). In this case, to calculate protections with a time delay of the order of 1-2 s or more, it would be necessary to use a steady short-circuit current. However, since the Calculation of the steady current short circuit. relatively complex, it is permissible in most cases to use the initial short-circuit current. Such an assumption, as a rule, does not lead to a large error. This is explained as follows. On the value of the steady current to. much more than the value of the initial current, have an increase in contact resistance at the fault site, load currents, and other factors that are usually not taken into account when calculating short-circuit currents. Therefore, the calculation of the steady current short circuit. may have a very large error.
Taking into account all of the above, it can be considered appropriate and in most cases quite acceptable to use for the analysis of relay protections operating with any time delay, the initial short-circuit current. In this case, the possible decrease in current during a short circuit should be taken into account for protections with a time delay by introducing into the calculation increased reliability factors compared to high-speed protections.
b) Determination of the initial short-circuit current. in a simple scheme
Since with a three-phase short circuit. (Fig. 1-24) e. d.s. and the resistances in all phases are equal, all three phases are in same conditions. vector diagram for such a short circuit, which, as is known, is called symmetrical, is shown in Fig. 1-18, b. Calculation symmetrical circuit can be greatly simplified. Indeed, since all three phases are under the same conditions, it is sufficient to make a calculation for one phase and then extend the results to the other two. The calculation scheme in this case will have the form shown in Fig. 1-24, b. It is quite obvious that even in the simplest case under consideration, the latter circuit is much simpler than that shown in Fig. 1-24 a.

In difficult ones electrical circuits, which have many parallel and serial branches, the difference will be even more obvious.
So, in a symmetrical system, the calculation of currents and voltages can be made only for one phase. The calculation begins with the preparation of an equivalent circuit, in which the individual elements of the calculation circuit are replaced by the corresponding resistances, and for power supplies their e is indicated. d.s. or clamp voltage. Each element is introduced into the equivalent circuit with its active and reactive resistances. The resistances of generators, transformers, reactors are determined on the basis of passport data and are entered into the calculation, as indicated below.
The reactive resistances of power lines are calculated using special formulas or can be taken approximately according to the following expression:
where l is the length of the line section, km; х ud - line reactive resistance, Ohm/km, which can be taken equal to:
In the future, to simplify the reasoning, we will assume that the condition (1-23), which, as a rule, is satisfied for networks with a voltage of 110 kV and above, is valid, and we will only introduce into the calculations reactances calculation scheme.
Determination of short-circuit current when powered by an unlimited power system. Current short circuit in the design scheme (Fig. 1-25) will be determined according to the following expression, kA:
where x res is the resulting resistance to the short circuit point, which in this case is equal to the sum of the resistances of the transformer and the line, Ohm;
U with - phase-to-phase voltage on the buses of the system of unlimited power, kV.
The definition of an unlimited power system means a powerful power source, the voltage on the buses of which remains constant regardless of the location of the short circuit. in the external network. The resistance of the system of unlimited power is assumed to be zero. Although in reality there cannot be a system of unlimited power, this concept is widely used in the calculation of short circuits. We can assume that the system under consideration has unlimited power in those cases when its internal resistance much less than the resistance of external elements connected between the system buses and the short circuit point.
|
Example 1-1. Determine current. passing at a three-phase short circuit behind the reactor with a resistance of 0.4 Ohm, which is connected to the tires of the generator voltage of 10.5 kV of a powerful power plant.
Solution. Since the resistance of the reactor is much greater than the resistance of the system, it can be considered that it is connected to buses of unlimited power.

Determination of short-circuit current when powered by a system of limited power. If the resistance of the system supplying the short circuit point is relatively large, it must be taken into account when determining the short circuit current. In this case, an additional resistance x spst is introduced into the equivalent circuit and it is assumed that there are buses of unlimited power behind this resistance.
The magnitude of the current short circuit is determined by the following expression (Fig. 1-26):
where x ext is the resistance of the short circuit between the tires and the short circuit point; x syst - the resistance of the system, reduced to the busbars of the source.
The system resistance can be determined if the three-phase short circuit current is set. on its tires I k.z.zad. :
Example 1-2. Determine the current of a three-phase short circuit. behind the 15 ohm resistance of the 110 kV line, powered by the busbars of the substation. Three-phase short circuit current on the busbars of the substation, reduced to a voltage of 115 kV, is 8 kA.
Solution. According to (1-26), x syst is determined:
![]()
The current is determined in the place of short circuit. according to (1-25):
|
System resistance in short circuit calculations can be set not by the current, but by the short circuit power on the substation buses. Short circuit power - a conditional value equal to
where I k.z. - short circuit current; U cp is the average rated voltage at that stage of transformation where the short circuit current is calculated.
Example 1-3. Determine the current of a three-phase short circuit. behind the reactor with a resistance of 0.5 ohms. The reactor is powered by 6.3 kV buses of the substation, the power of the short circuit. which is equal to 300 MB A.
Solution. Let's define the resistance of the system:
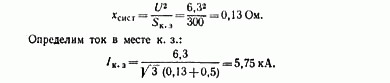
c) Determination of residual stress
In the diagram shown in fig. 1-26, the amount of residual voltage on the tires is determined according to the following expressions:
x is the resistance from the power supply busbars to the point where the residual voltage is determined.
Since the resistance of the circuit under consideration is assumed to be purely reactive, expressions (1-27) and (1-28) include absolute values, and not vectors.
Example 1-4. Determine the residual phase-to-phase voltage on the substation buses in example 1-2.
Solution. According to the first expression (1-27):

d) Calculations of short circuit currents and voltages in an extensive network
In a complex branched network, in order to determine the current at the fault location, it is necessary to first convert the equivalent circuit so that it has a simple form, if possible with one power source and one branch of resistance. For this purpose, the branches connected in series and in parallel are added, the resistance triangle is converted into a star and vice versa.
Example 1-5. Convert the equivalent circuit shown in fig. 1-27, determine the resulting resistance and current at the location of the short circuit. The resistance values are shown in fig. 1-27.
Solution. The equivalent circuit is converted in the following sequence.

For distribution of current to. on the branches of the circuit, you can use the formulas given in Table. 1-1. The distribution of currents is carried out sequentially in reverse order starting from the last stage of equivalent circuit conversion.
Example 1-6. Distribute short circuit current along the branches of the scheme shown in fig. 1-27.
Solution. Let's determine the currents in parallel branches 4 and 7 in accordance with the formulas (Table 1-1):


The current I 7 passes through the resistance x 5 and then branches along the parallel branches x 2 and x 3:

The residual voltage at any point in a branched circuit can be determined by successively summing and subtracting the voltage drops in its branches.
Example 1-7. Determine the residual voltage at points a and b of the circuit shown in fig. 1-27. Solution.

If e. d.s. not equal, equivalent e. d.s. calculated using the following formula:
|
e) Calculation of short circuit currents according to passport data of reactors and transformers
In all the examples discussed above, the resistances individual elements the circuits were given in ohms. The resistances of reactors and transformers in passports and catalogs are not specified in ohms.
Reactor parameters are usually set as a percentage as the relative value of the voltage drop in it during the passage of the rated current x P,%.
Reactor resistance (Ohm) can be determined by the following expression:
|
where U HOM and I HOM - Rated voltage and reactor current.
The resistance of the transformer is also given as a percentage as the relative value of the voltage drop in its windings during the passage of a current equal to the nominal one, u K , %.
For a two-winding transformer, you can write the resistance (Ohm):
where u K , %, and U HOM , kV, are indicated above, and S HOM is the rated power of the transformer, MB A.
In the event of a short circuit behind a reactor or transformer connected to the system buses of unlimited power, the current and power short circuit. are defined by the following expressions:
![]()
where I HOM - rated current appropriate reactor or transformer.
Example 1-8. Calculate the maximum possible current of a three-phase short circuit. behind the RBA-6-600-4 reactor. The reactor has the following parameters: U H = 6 kV, I H = 600 A, x P = 4%.
Solution. Since it is required to determine the maximum possible short circuit current, we assume that the reactor is connected to the buses of the system of unlimited power.
According to (1-33) short circuit current. behind the reactor is defined as
Example 1-9. Determine the maximum possible current and power of a three-phase short circuit. behind the step-down transformer: S, H = 31.5MB A, U H1 = 115 kV, U H2 = 6.3 kV, u K = 10.5%
Solution. Assuming, as in the previous example, that the transformer is connected from the side of 115 kV to the buses of the unlimited power system, we determine the short-circuit current.
The rated current of the 6.3 kV winding of the transformer is equal to.